Open Journal of Statistics
Vol.08 No.02(2018), Article ID:83720,18 pages
10.4236/ojs.2018.82018
Extending the Behrens-Fisher Problem to Testing Equality of Slopes in Linear Regression: The Bayesian Approach
Mohamed Shoukri*, Futwan Al-Mohanna
Department of Cell Biology, National Biotechnology Center, Research Centre, King Faisal Specialist Hospital and Research Center, Riyadh, Saudi Arabia

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 12, 2018; Accepted: April 10, 2018; Published: April 13, 2018
ABSTRACT
Testing the equality of means of two normally distributed random variables when their variances are unequal is known in the statistical literature as the “Behrens-Fisher problem”. It is well-known that the posterior distributions of the parameters of interest are the primitive of Bayesian statistical inference. For routine implementation of statistical procedures based on posterior distributions, simple and efficient approaches are required. Since the computation of the exact posterior distribution of the Behrens-Fisher problem is obtained using numerical integration, several approximations are discussed and compared. Tests and Bayesian Highest-Posterior Density (H.P.D) intervals based upon these approximations are discussed. We extend the proposed approximations to test of parallelism in simple linear regression models.
Keywords:
Bayesian Inference, Posterior Distributions, Behrens-Fisher Problem, Posterior Moments, Edgeworth Expansion, Monte-Carlo Integration

1. Introduction
Suppose that x1 and x2 are two independent normal random variables with means μ1 and μ2, and variances and , respectively. Samples of sizes n1 and n2 drawn from the corresponding populations are denoted by ( and ). It is desired to test the hypothesis H0: μ1 = μ2 when it cannot be taken as known that the variance ratio is one. This problem, known as the Behrens-Fisher (BF) problem, has been investigated by many authors and each has proposed some particular solution. It is not the purpose of this paper to list or survey these solutions. However, the Bayesian approach to this problem, viewed as one of the most fascinating approaches of statistical inference on the means of heterogeneous normal populations, will be the main focus of this paper, and we shall also give special attention to the problem of testing parallelism of two linear regression lines when the variances of the error terms are not equal.
The exact Bayesian solution to the BF problem was given by Jeffreys [1] which was identical to the solution of Behrens [2] and Fisher [3] . The resulting posterior distribution of , which is the primitive of a valid Bayesian procedure, possesses a form requiring an integration that cannot be performed analytically, and hence, direct and routine implementation of this test is impossible. Although evaluation of such an integral can be achieved numerically, using the approaches described by Reilly [4] and Naylor and Smith [5] , and by Monte-Carlo integration as given in Robert and Casella [6] it is of interest to provide expressions for routine applications under the Bayesian approach.
The paper has two chief objectives. First we present a comparison among several approximations to the tails of the posterior distribution of the variate , where μj is the mean of the jth population. Second we extend the methodologies to address the question of parallelism or equality of slopes when the variances of the error terms of the two regression lines are not equal. Recommendations will follow the examples in the last sections.
2. Testing Equality of Normal Means: Posterior Analysis
Based on the samples outcome, the usual sufficient statistics are defined as follows:
and , .
The likelihood function of the combined data from two samples drawn independently from two normal populations with means μ1 and μ2, and variances and , respectively, is proportional to:
. (2.1)
Following Lee [7] , we use the non-informative prior for the means and the standard deviations
(2.2)
From Box & Tiao [8] , the joint posterior density of is the product of (2.1) and (2.2) and is then given by:
(2.3)
Integrating out of (2.3), the marginal posterior density of is shown to be
(2.4)
The conditioning in Equation (2.4) is on the represents the data vector x.
Equation (2.4) was obtained by Jeffreys [1] . In the Bayesian approach, inferences about U are completely determined by (2.4), which is not amenable to simple manipulation in order to have the tests on U conducted in a routine fashion. Before applying some of the suggested approximations, we should understand the nature of the problem, and in order to draw safe conclusions, we consider not only the marginal posterior density of u, but also we need to examine the other components of (2.3). For this purpose, we state the following results without proof, since they are easily obtained by application of the calculus of probability:
1) The conditional posterior pdf for U, given μ2, is the univariate student’s , with mean and variance , i.e.,
. (2.5)
2) The marginal posterior pdf for the variance ratio λ is such that has the well-known Snedecor’s F-distribution with , and degrees of freedom, i.e.,
(2.6)
3) The conditional posterior pdf for U, given λ, is such that
(2.7)
where , i.e., it has student’s t density with
degrees of freedom. Hence as was indicated by Barnard [9] , if a range of λ values is considered plausible, λ can be varied over this range to see what effect this variation has on the value of t. He also postulated that when n1 and n2 are nearly equal, and moderately large, and and do not differ much, the conditional distribution in (2.7) will remain nearly constant over a wide range of λ values. In the next section we derive different approximations to deal with the situation when the range of λ is wide enough to have a considerable effect on t.
3. Approximate Posterior Inference
3.1. Monte Carlo Integration (Exact Approximation)
We shall write the posterior density of U as follows:
(3.1a)
In (3.1a) we face the same problem as we have with (2.4), however, this equation will be the tool of discussion in the remainder of this section. As can be seen evaluation of the posterior density of U is just evaluating the integral in (3.1a) which can be written as:
(3.1b)
Referring to Robert and Casella [6] , the principle of the Monte Carlo method for approximating (3.1b) is to generate sample from their density and suggest as an approximation the empirical average
(3.2)
3.2. Moments (Scale) Approximation
The second approximation to be considered is by the method of moments. While Patil [10] derived the posterior moments of U using (2.4), they are identical to the posterior moments
. (3.4)
Denoting the rth central moment of U by , and its 4th cumulant by , we can show from Equation (3.4) that
,
The fourth cumulant is:
(3.5)
Following Patil [10] , we suggest the following approximation to the posterior distribution of δ:
. (3.6)
Equating m2 and m4 to the second and fourth central moments of the R.H.S. of ~ in (3.6) we have:
and .
In the above equation [s] means the smallest integer larger than s. Thus one may use tables of student’s t-distribution with [b] degrees of freedom to make tests and construct approximate H.P.D. intervals for U. In other words:
3.3. Modal Approximation
Barnard [9] suggested that if the intention is to make inference on U alone by integrating out λ and it is found that is very sensitive to changes in λ, then should be carefully examined. If were sharp with most of its probability mass concentrated over a small region about its mode denoted by λ*, performing the numerical integration in (3.1a) will be nearly equivalent to assigning the model value to λ in the conditional density, so that:
. (3.7)
Now, since , then substituting in (3.7) we have:
, (3.8)
where
.
Therefore, as a modal approximation to the posterior distribution of we take:
. (3.9)
3.4. Approximation Based on Averaging
The following lemma due to Feller is quite appealing and may be used to approximate the integral (3.1a):
Lemma: Feller ( [11] , p. 219). For , consider a family of distributions with expectation Θ and variance (that is the variance is a function of the mean). If is bounded and continuous, and for each Θ, then
. (3.10)
Since and with as , then by taking as and as the right hand integral of (3.1a) can be approximated by:
,
where
.
Accordingly, one may take
. (3.11)
as an approximating distribution to the posterior distribution of U.
3.5. Edgeworth Expansion
The Edgeworth expansion has been used extensively by many authors in order to approximate the density function of any statistics . We refer to the paper by Barndorff-Nielson and Cox [12] for an overview and comparison between these techniques. The Edgeworth expansion, due to Edgeworth [13] [14] , for the
density function of any statistic at a point c is given by the general formula:
where and are respectively the coefficients of skewness and Kurtosis for the density of . As can be seen when , the terms of order disappear and the modified Edgeworth expansion of order for the density function of the statistic at c is given by:
. (3.12)
The Edgeworth expansion for the density of U can easily be obtained, from Equation (3.12), by using linear transformation, .
Although we are not approximating the distribution function directly, in practice these approximations may be used for calculating tail areas. Thus it is of interest to see how these approximations for the posterior distributions of perform at the tail.
Example 1: “Mean tumor recurrence scores in breast cancer patients stratified by tumor grades.”
Oncotype DX is a commercial assay used for making decisions regarding the treatment of breast cancer. The results are reported as a tumor recurrence score ranging from 0 to 100, Klein et al. [15] showed that the recurrence score correlated (among other genetic factors) with the tumor grade. That is there was a significant difference in the mean recurrence scores in patients with tumor grade 1 as compared to the mean recurrence score of patients with tumor grade 3. In this example we present the summary data for 40 and 37 breast cancer women samples with mean recurrence scores in tumor rage 1 and tumor grade 3. This data is a good example that we can use to apply the proposed methodology. The following results were obtained:
, ,
, ,
Approximations, discussed in section 3, to the posterior density of are applied to the above data. In addition we also consider the usual asymptotic normal approximation which for large n1 and n2, is given as suggested by Welch [16] as:
,
The results of the data analyses based on the proposed approximations are presents in Table 1.
As we can see, all approximations have confidence limits close to the exact limits, probably because the sample sizes are moderately large. We provide the R-codes for the calculations of these limits in the Appendix within the applications of linear regression.
4. Extension of the Behrens-Fisher Problem to Testing Equality of Slopes of Two Independent Regression Lines
Linear and nonlinear regression models are ubiquitous in medical and biological research. Testing equality of slopes of two linear regression lines is of special interest. This is illustrated in the following application which is a continuation of example 1.
Table 1. Approximate 95% HPD for the difference in two means under heterogeneity using the breaking strength data.
Example 2: continuation of example 1.
Ki67 is a commonly used marker of cancer cell proliferation, and has significant prognostic value in tumor recurrence of breast cancer. In this illustration which is a continuation to example 1, we use a sub-sample of women who had Oncotype DX testing performed and available Ki67 indices which correlated with tumor grades (1 versus 3). Literature documented that Ki67 scores contribute significantly to models that predict risk of recurrence in breast cancer, for example see; Cuzick et al. [17] , Klein et al. [14] , and more recently Thakur et al. [18] . In this example we examine the relationship between Ki67 as predictor of tumor recurrence scores of breast for tumor grade 3 and grade 1 separately. Of interest is to test the equality of the slopes of the linear regressions of tumor recurrence score on the Ki67 for both grades. We use Bayesian methodology to answer this question.
We shall use the following notations. First we denote the independent variable by x to predict values of the dependent variable denoted by y.
Suppose that we have two linear regression lines, then conditional on we assume that
, & .
In general we assume that we have two conditions, and we would like to estimate .
In our Bayesian analysis we shall take a reference prior that is independently uniform in and , such that:
Let us define the following quantities:
, , ,
where
, , ,
and
.
The joint posterior distribution of the model parameters are proportional to
(4.1)
For the two regression lines, the joint posterior of is , or
(4.2)
Integrating out and , the joint posterior of is thus given as:
Integrating out and we get:
(4.3)
Under the transformation , one can show that the posterior density of δ is given by:
(4.4)
where .
The Bayesian inferences on δ are completely determined by Equation (4.4) which we cannot easily manipulate in order to have statistical inferences test on δ conducted in a routine fashion. Moreover, it is clear from (4.4) that the exact
marginal posterior distribution of is that of a Student t-distribution with rj degrees of freedom.
Similar to testing the equality of means of two normally distributed distributions and as shown in the first part of the paper, we use the suggested approximations to the integral given in (4.4) to find the marginal posterior distribution of δ. However, it is quite helpful to not only examine the posterior density of δ, but also examine the components of the joint posterior density given in (4.4). For this purpose, we state the following results without proof, since they can be easily obtained by applications of the calculus of probability.
1) The conditional posterior p∙d∙f of δ, given is the univariate Student-t with ( ), with conditional mean and conditional variance .
The unconditional posterior mean and variance of δ are:
2) The marginal posterior p∙d∙f of the variance ratio λ is a scale multiplicative of the F-distribution. That is:
Therefore, the posterior moments of λ are:
Using the inverse moments of the F-distribution we can show that:
(4.5)
and
3) The conditional posterior p∙d∙f of δ, given λ is such that
(4.6)
These results are derived based on the fact that conditional on λ, the posterior distribution of
Is that of a t-distribution with degrees of freedom.
5. Approximating the Posterior Distribution of δ
5.1. Moments Approximation (Scale Approximation)
As a first approximation to the posterior distribution of is to assume that
(5.1)
Equating and to the second and fourth control moments of the R∙H∙S of in (5.1) we get:
Here, and mean the smallest integer larger than ξ. Thus one may use tables of student’s t-distribution with degrees of freedom to construct H.P.D. intervals on δ. As can be seen this result is identical to the moment or the scale approximation of the posterior distribution of the difference between means.
5.2. Modal Approximation
As suggested by Box and Tiao [8] , we approximate the posterior density on replacing λ by its modal value so that:
(5.2)
Hence we take
(5.3)
As a t-statistic with degrees of freedom, where and , and is the modal value of λ.
5.3. Approximation Based on Averaging
Here we find that the conditions of Feller’s [8] lemma are satisfied by the two central moments of . This is because: and with as .
By taking as and as , the R.H.S. of (5.2) can be approximated by
where
Hence, we take
where
We now analyze the data in this example. We take the Ki67 to be the explanatory variable (x), while the recurrence score is the dependent variable (y). The tumor grades 1 and 3 form the two groups whose slopes are to be compared. The summary data are:
Tumor grade 1 Tumor grade 3
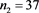
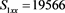

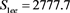
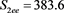
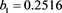
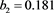
The scatter plots are given for tumor grade 1 (Figure 1) and for tumor grade 3 (Figure 2)
Figure 1. Scatter plot of recurrence score against Ki67 for tumor grade 1.
Figure 2. Scatter plot of recurrence score against Ki67 for tumor grade 3.
As we can see, for tumor grade 1, the association between Ki67 and tumor recurrence is quite weak, but the association is stronger for tumor grade 3.
Remarks:
For all the proposed methods, our data analysis approach is simulation-based. The number of replications used is sufficient. For the Monte-Carlo integration, which we consider to be the exact we monitored the simulation. As we can see in Figure 3 the sequence of simulations tends to stabilize as we approach the specified number of simulations.
We should note that the red line bands in Figure 3 are not 95% confidence bands in classical sense, but they correspond to the confidence assessment that is produced for every number of iteration, if we decide to stop at this number of iterations. The 2.5% and 97.5% quantiles for the methods are shown in Table 2.
6. Discussion
In the data analytic part, one may be interested in the shape of the density of the approximating distributions and how they deviate from the exact density. We did not discuss this issue since most of the time we are interested in the tail area
Figure 3. Monitoring the approximation of the function 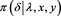 with mean ± two standard deviations against the iterations for a single sequence of simulations.
with mean ± two standard deviations against the iterations for a single sequence of simulations.
Table 2. Approximate 95% HPD for the difference in two slopes of linear regression lines heterogeneity using the Tumor recurrence scores data.
of the distribution in order to construct confidence intervals on the mean difference or the difference of slopes. From Table 1 and Table 2, we can see that all the approximations perform well when compared to the exact limits. However, the scale approximation, which uses the first 4 central moments, provides more accurate confidence limits. The modal approximation seems to err in the upper limits of difference between the target parameters. Our general conclusion is that when the sample sizes are reasonably large as in the breast cancer example all the approximations (except the modal) may be used. For sample sizes and routine implementation of the proposed test, the scale (the four moments) approximation is recommended.
Conflict of Interest
None declared by all authors.
Cite this paper
Shoukri, M. and Al-Mohanna, F. (2018) Extending the Behrens-Fisher Problem to Testing Equality of Slopes in Linear Regression: The Bayesian Approach. Open Journal of Statistics, 8, 284-301. https://doi.org/10.4236/ojs.2018.82018
References
- 1. Jeffreys, B. (1940) Note on the Behrens-Fisher Formula. Annals of Eugenics, 10, 48-51. https://doi.org/10.1111/j.1469-1809.1940.tb02236.x
- 2. Behrens, W.V. (1929) Ein Beitragzur Fehlerberechunung bei Weniger Beoachtungen. Landw. Jb., 68, 807-837.
- 3. Fisher, R.A. (1939) The Comparison of Samples with Possibly Unequal Variances. Annals of Eugenics, 9, 174-180. https://doi.org/10.1111/j.1469-1809.1939.tb02205.x
- 4. Reilly, P.M. (1976) The Numerical Computation of Posterior Distributions. Applied Statistics, 25, 201-209. https://doi.org/10.2307/2347227
- 5. Naylor, J.C. and Smith, A.F.M. (1982) Applications of a Method for the Efficient Computation of Posterior Distributions. Applied Statistics, 31, 214-225. https://doi.org/10.2307/2347995
- 6. Robert, C. and Casella, G. (2009) Introducing Monte Carlo Methods with R. Springer, New York.
- 7. Lee, P.M. (1989) Bayesian Statistics: An Introduction. Oxford University Press.
- 8. Box, G.E.P. and Taio, G.C. (1973) Bayesian Inference in Statistical Analysis. Addison-Wesley Publishing Company, Inc., Reading, Mass.
- 9. Barnard, G.A. (1984) Comparing the Means of Two Independent Samples. Applied Statistics, 33, 266-271. https://doi.org/10.2307/2347702
- 10. Patil, V.H. (1964) The Behrens-Fisher Problem and Its Bayesian Solution. Journal of the Indian Society for Probability and Statistics, 2, 21-31.
- 11. Feller, W. (1971) An Introduction to Probability Theory and Its Applications. 2nd Edition, John Wiley & Sons, Inc., New York.
- 12. Barndorff-Nielson, O. and Cox, D.R. (1979) Edgeworth and Saddle-Point Approximations with Statistical Applications. Journal of the Royal Statistical Society: Series B, 41, 279, 312.
- 13. Edgeworth, F.Y. (1896) The Asymmetrical Probability Curve. Philosophical Magazine, 5th Series, 41, 90-99.
- 14. Edgeworth, F.Y. (1907) On the Representation of Statistical Frequency by Series. Journal of the Royal Statistical Society: Series A, 70, 102-106. https://doi.org/10.2307/2339504
- 15. Klein, M.E., Dabbs, D.J., Shuai, Y., Brufsky, A.M., Jankowitz, R., Puhalla, S.L., et al. (2013) Prediction of the Oncotype DX Recurrence Score: Use of Pathology-Generated Equations Derived by Linear Regression Analysis. Modern Pathology, 26, 658-664.
- 16. Welch, B.L. (1937) The Significance of the Difference between Two Means when the Population Variances Are Unequal. Biometrika, 34, 28-35.
- 17. Cuzick, J., Dowsett, M., Pineda, S., Wale, C., Salter, J., Quinn, E., et al. (2011) Prognostic Value of a Combined Estrogen Receptor, Progesterone Receptor, Ki-67, and Human Epidermal Growth Factor Receptor 2 Immuno-Histochemical Score and Comparison with the Genomic Health Recurrence Score in Early Breast Cancer. Journal of Clinical Oncology, 29, 4273-4278.
- 18. Thakur, S.S., Li, H.C., Angela, M.Y., Chan, R.T., Bigras, G., Morris, D., Enwere, E.K. and Yang, H. (2018) The Use of Automated Ki67 Analysis to Predict Oncotype DX Risk-of-Recurrence Categories in Early-Stage Breast Cancer: January 5, 2018. PLOS ONE.
Appendix: R Codes for the Regression Model. The Codes for the Comparison between Means Is Quite Similar and Not Included
R-CODES.
#Summary data
n1=40, n2=37, s1xx=1019.6, s2xx=11167.57, s1ee=700.13, s2ee=3931.172
b1=.124, b2=.447.
#Monte Carlo integration
sig1=(n1-2)*s1ee/s1xx
sig2=(n2-2)*s2ee/s2xx
T2=(sig1/((n1-2)*(n1-4)))+(sig2/((n2-2)*(n2-4)))
ll=rf(10000,n2-2,n1-2) #simulating from the F-distribution
l=ll*(s1ee/s2ee)*((n2-2)/(n1-2))
A=s1xx/(s1ee+l*s2ee)
B=l*s2xx/(s1ee+l*s2ee)
nn=n1+n2-4
beta1=b1+rt(10000,n1-2)*sqrt(sig1/((n1-2)*(n1-4)))
beta2=b2+rt(10000,n2-2)*sqrt(sig2/((n2-2)*(n2-4)))
delta=(beta1-beta2)
q1=quantile(delta,prob=c(0.025,0.975))
q1
#Monitoring the simulation
h=function(x){(1/(1+((A*B)/(A+B))*(x-b1+b2)^2)^(((nn+1)/2)))}
x=h(l)
estint=cumsum(x)/(1:10^4)
mean(estint)
esterr=sqrt(cumsum((x-estint)^2))/(1:10^4)
mean(esterr)
plot(estint,xlab="Mean and error range",lwd=2,
ylim=mean(x)+20*c(-esterr[10^4],esterr[10^4]),ylab="")
lines(estint+2*esterr,col="red",lwd=2)
lines(estint-2*esterr,col="red",lwd=2)
#Moments (Scale) Approximation
sig1=(n1-2)*s1ee/s1xx
sig2=(n2-2)*s2ee/s2xx
T2=(sig1/((n1-2)*(n1-4)))+(sig2/((n2-2)*(n2-4)))
T41=3*sig1^2/((n1-2)^2*(n1-4)*(n1-6))
T42=3*sig2^2/((n2-2)^2*(n2-4)*(n2-6))
T412=6*sig1*sig2/((n1-2)*(n1-4)*(n2-2)*(n2-4))
T4=T41+T42+T412
K4=T4-3*T2^2
a=sqrt(T2*T4/(T4+K4))
b=ceiling(2*(1+(T4/K4))) #integer degrees of freedom
d=rt(10000,b)
delta.m=(b1-b2)+a*d
q2=quantile(delta.m,prob=c(.025,.975))
q2
#Welch Normal Approximation
zz=rnorm(10000)
u=(b1-b2)+zz*sqrt(T2)
mean.u=mean(u)
sd.u=sd(u)
qqnorm(u)
q3=quantile(u,prob=c(0.025,0.975))
q3
#Edgeworth expansion
library(distr)
aa=K4/(24*T2^2)
p <- function(x) (1/sqrt(2*pi) *(1/(exp(x^2/2)*
(1+aa*(x^4-6*x^2+3)))))
# probability density function
dist <-AbscontDistribution(d=p) # signature for a distribution with pdf ~ p
rdist <- r(dist) # function to create random variates from p
set.seed(1)
XX <- rdist(10000) # sample from X ~ p
x <- seq(-10,10, .01)
hist(XX, freq=F, breaks=50, xlim=c(-5,5))
lines(x,p(x),lty=2, col="red")
mean(XX)
sd(XX)
edgeworth=b1-b2+sqrt(T2)*XX
hist(edgeworth)
q4=quantile(edgeworth,prob=c(0.025,.975))
q4
#Averaging approximation based on Feller’s lemma
nu=n1+n2-4
f=rf(10000,n2-2,n1-2)
t=rt(10000,nu)
l=(s1ee/s2ee)*f
mean.l=mean(l)
denom=s1ee+mean.l*s2ee
A=s1xx/denom
B=mean.l*s2xx/denom
d.mean=(b1-b2)+ (sqrt((A+B)/(A*B))*t)/sqrt(nu)
q5=quantile(d.mean,prob=c(.025,.975))
q5
#Modal approximation
ff=rf(10000,n2-2,n1-2)
f=ff*s1ee*(n2-2)/s2ee*(n1-2)
m=(s1ee/s2ee)*(n2-4)/n1
nu=n1+n2-4
t=rt(10000,nu)
denom=s1ee+m*s2ee
AA=s1xx/denom
BB=m*s2xx/denom
d.mod=(b1-b2)+ (sqrt((AA+BB)/(AA*BB))*t)/sqrt(nu)
q6=quantile(d.mod,prob=c(.025,.975))
q6





