Open Journal of Statistics
Vol.06 No.04(2016), Article ID:69743,11 pages
10.4236/ojs.2016.64051
Quantifying the Microeconomic and Macroeconomic Impact of the Recent Crude Oil Price Fluctuations
Peng Xu, Utsav Adhikari, Lei Guo, Deepa Sathaye, Jihua Wang, Dongliang Yi, Yizhi Zhu
Department of Industrial and Enterprise Systems Engineering, University of Illinois, Urbana, IL, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 May 2016; accepted 1 June 2016; published 15 August 2016
ABSTRACT
This study analyzed the potential impact of the increased oil volatility on the industries and the global economy. Specifically, it separated the oil price fluctuations into positive and negative components, and modeled the return of industry portfolios with them. Next, the sensitivity of the airline industry to oil price was investigated to gauge the effectiveness of their hedging strategies, with the hope that the methodology can be extended to other industries. In addition, this paper explored the macroeconomic impact of oil price movements by examining the benchmarks such as GDP and CPI.
Keywords:
Crude Oil, Airline, Hedging, Asymmetric Effects, Microeconomics, Macroeconomics

1. Introduction
During the past 2 years, the crude oil price has undergone a drastic change: it has fallen from over $100 per barrel, to below $28, a 10-year low recorded in January 2016, and then bounced back to the current level of $45; Figure 1 visualized this ongoing trend. Effect of this oil price fluctuation on the economy is profound: Various industries have experienced the benefits and obstructions caused by the price shock; while consumers may gain from the lowering prices, disruptions in the financial market may come back and depress their confidence, as pointed out in a recent article [1] .
The goal of this article is to quantify the impact of the oil price in certain industries with the available historical data, and then analyze the impact of oil price changes on the current domestic and global market. In
Figure 1. Daily WTI Cushing spot price since 2010.
Section 2, return of several industries were investigated in order to measure their sensitivities to change of oil price. Afterwards, the analysis was narrowed down to the airline industry to look into the effectiveness of their hedging strategies on jet fuel. Finally, in Section 3, the effects of the recent oil price fluctuation on GDP of several countries and CPI of the United States were explored.
2. Microeconomic Analysis of the Impact
2.1. Sensitivity of Industry Return to Oil Price
Intuitively, certain businesses, such as oil refinery and transportation operator, are strongly impacted by the oil price fluctuations, since petroleum products are direct inputs to their operation. However, to others, such as apparel and computer software manufacturer, it is very difficult to judge whether their performances were affected by the oil price shock at all. The subsequent analyses in this section attempts to measure these potential impacts quantitatively.
The following model was selected to analyze the impact of oil price change on different industries:
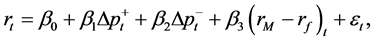 (1)
(1)
where r denotes the industry return, 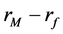 denotes the market risk-premium and p denotes the oil price. Additionally, we have included the following in the model:
denotes the market risk-premium and p denotes the oil price. Additionally, we have included the following in the model:
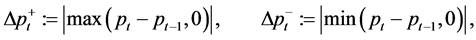
in order to capture the asymmetric effect of oil price movements. These variables represent the magnitudes of oil price increase and decline. In this way, 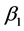 and
and  measure the sensitivity of industry return to the surge and shock of oil price. The significance of asymmetric effect is noted in many studies, such as [2] - [4] . This breakdown allows us to look at the different industry sensitivities more granularly so that we can estimate the sensitivity of oil price better.
measure the sensitivity of industry return to the surge and shock of oil price. The significance of asymmetric effect is noted in many studies, such as [2] - [4] . This breakdown allows us to look at the different industry sensitivities more granularly so that we can estimate the sensitivity of oil price better.
The analysis was conducted with the help of Kenneth R. French’s industry returns and market premium data. WTI Cushing spot price index obtained via Bloomberg terminal (Bloomberg terminal is a popular way to extract the latest real-time financial data in the field of finance) is used as the benchmark for oil price instead of others for its relevance to US market. The impact of oil price on stocks in various industries was estimated for all 1397 trading days between 2010-01-01 and 2015-07-31. It shall be noted though, that we did not adopt the popular Fama-French model for two reasons: first, some literatures (e.g. [5] ) advise against blindly expanding regression model; second, SMB (Small Minus Big) and HML (High Minus Low) factors are not always statistically significant (for example, SMB is insignificant in the analysis for the retail industry and HML is insignificant for the transportation industry) in the model; and even when they are, they barely affect the 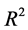 and other estimates.
and other estimates.
Various methods and tests, including Breusch-Pagan and Durbin-Watson, were applied to check the assumptions of our linear model. This paper found that model (1) does not suffer from autocorrelation, hetero- scedasticity, non-normal residuals, etc. Table 1A shows the regression results for various industries. In addition, the standard errors of 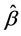 s, as a measurement of the “estimation risk”, are shown in Table 2A.
s, as a measurement of the “estimation risk”, are shown in Table 2A.
According to the results demonstrated, this model works reasonably well for most industries. Some industries, such as Agriculture, Automobiles, and Finance, have high p-value for their oil 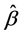 s (
s (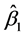 or
or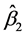 ), which suggests that these industries are not sensitive to the oil price increase or decrease, or at least a linear relationship between oil price and industry performance is not observed. On the other hand, some industries, such as Machinery and Transportation, experience opposite effects to the oil price movement such that there are losses when oil price increases and profits when the oil price declines, which intuitively makes sense because oil prices are direct inputs to the industry.
), which suggests that these industries are not sensitive to the oil price increase or decrease, or at least a linear relationship between oil price and industry performance is not observed. On the other hand, some industries, such as Machinery and Transportation, experience opposite effects to the oil price movement such that there are losses when oil price increases and profits when the oil price declines, which intuitively makes sense because oil prices are direct inputs to the industry.
In the next section, a further analysis was performed focusing on the air transportation industry for its transparency in sharing its cost structure, which enabled a more thorough study. The airline industry is ex- tremely competitive and the oil price shocks affect all the airlines. Hence its effects on each individual firms are not equivalent.
2.2. Hedging Effectiveness of Air Transportation Industry
The air transportation industry is a large consumer of petroleum products. According to IATA’s (International Air Transport Association) Annual Review 2015, fuel cost constitute on average approximately 29% of an airline's total operating cost in 2014, which means jet fuel price risk is economically significant to airlines. As a result, air transportation companies often choose to hedge in order to reduce their oil price risks.
In this section, the air transportation industry was used as an example to demonstrate a new method of comparing hedging strategies. Annual reports of several airlines were obtained via EDGAR (Electronic Data Gathering, Analysis, and Retrieval) and reviewed to determine their hedging status. The 10-K and 10-Q reports were used for US airlines while 20-F filings was used for the international airlines.
Most airlines use financial derivatives, such as swaps and options, to cover their oil price exposure. Other means to bypass the price risk includes fixed fee agreements and fuel surcharge programs, which pass the cost of oil upstream and downstream, respectively. Since airlines adopt various strategies to hedge oil price risks, it is difficult to evaluate the hedging effectiveness for the air transportation industry as a whole. Thus, six large companies (Table 1) were sampled from the US stock markets and paired together according to their market capitalization and hedging strategies, in order to analyze the efficiency of hedging strategies among airlines. Since the goal of hedging is to reduce the exposure to adverse price movement, this paper assumes that, for each pair, if one company's hedging strategy is indeed more effective than the other’s, their oil price sensitivities shall differ statistically, given that other factors are controlled.
For the comparison, model (1) was applied pairwise:
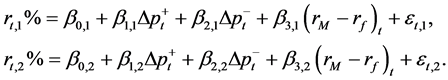 (2)
(2)
This time, however, the percentage return (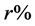 ) was used to scale the parameters by 100 times for the ease of the interpretation. For each airline, stock prices between 01-01-2014 and 12-31-2015 were pulled via Bloomberg Terminal, and their daily log-return was calculated. Again, WTI Cushing spot price index is used as the benchmark for oil price for its relevance. Further analysis shows that the returns of almost all airlines on 2014-11-28 were abnormal: the average return of sample airlines of the day reaches 6.4%, which is extremely
) was used to scale the parameters by 100 times for the ease of the interpretation. For each airline, stock prices between 01-01-2014 and 12-31-2015 were pulled via Bloomberg Terminal, and their daily log-return was calculated. Again, WTI Cushing spot price index is used as the benchmark for oil price for its relevance. Further analysis shows that the returns of almost all airlines on 2014-11-28 were abnormal: the average return of sample airlines of the day reaches 6.4%, which is extremely
Table 1. Selected companies for the analysis of hedging effectiveness.
high as it is almost 64 times of the mean return. It was deemed as an outlier and excluded from the data for the accuracy of our analysis. Table 2 reports the 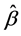 s of regression models after removing the outlier.
s of regression models after removing the outlier.
In order to determine whether the sensitivities of oil price really differ, this paper performed two-tailed tests for each pair of companies on the following hypotheses:
via Z-score proposed by [6] and permutation test (number of re-sampling is set to be 100,000). Table 3 shows the resulting p-values. They suggests that there is no strong evidence that one hedging strategy is more effective than the other except for Pair 2.
For the record, this paper also performed Chow’s test proposed by [7] on each pair of the regression model. The results shown in Table 4 are consistent with the analyses above; namely, it is difficult to tell the difference between strategies by companies in Pair 1 and 3.
For the first pair, the performances of hedging with financial derivatives and non-hedging were compared. The result shows that the coefficient of AAL’s return to oil price increase is insignificant, indicating that using financial derivative to hedge has no convincing effect. One reason is that since oil price kept decreasing in recent years, even if the oil price increase sometimes, most options are still out of money. The other reason is that the premium of derivatives and other cost may offset the benefit of hedging. We could also see the coefficient of AAL’s return to oil price decrease is marginally higher than the coefficient of LUV. If the difference does exist, AAL would be slightly more sensitive to oil price decrease and benefits more from the oil price shock. The unhedged companies could benefit directly from the oil price declines while hedging com- panies only benefit from their saved cost of unhedged exposure. All in all, it can be concluded that those without hedging have potential to outperform those who hedge during the oil price shock.
In the second pair, the sensitivities of FDX and DAL were compared in order to determine the effectiveness of surcharge programs versus financial derivatives. FDX’s service usually includes a fuel surcharge, so that the crude oil price risk was passed to their customers. For example, FDX adjusts its Express services surcharge percentage monthly, based on rounded average of the US Gulf Coast (USGC) spot price for a gallon of kerosene-type jet fuel. According to Table 2, the effect of both positive and negative oil price movements on FDX’s return are not significant, while DAL’s returns still subject to the oil price fluctuations. Thus, it can be inferred that the surcharge strategy of FDX was more efficient in reducing risk exposure and helped the company to keep a comparatively stable return.
In the third pair, the performances of SAVE and ALGT were used to analyze the effect of fixed fee agreement versus the financial derivatives. Fixed fee agreement is a type of contracts used by larger airlines or airports that outsource some of their routes and services to the smaller, regional airlines, as the two companies chosen in this pair. Fuel costs of the smaller airlines in the contract are often reimbursed, so their exposure to the risk of fuel price is effectively reduced. According to the regression coefficients, SAVE’s sensitivity to the positive oil price movement is less than that of ALGT, while SAVE could benefit more from the oil price decline, so obviously financial derivatives outperformed fixed fee agreement. Nevertheless, statistically it is difficult to distinguish them as revealed by the test results shown in Table 3. There are many reasons that explain the observation. For example, since ALGT’s agreement was signed with large airlines, the company has little bargaining power such that using agreement is not as flexible as using financial derivatives, which could impair the effectiveness. A more probable cause, however, is that other factors that affect the returns, such as cost structures, may not be
Table 2. Parameters estimates for model (2).
Table 3. Testing results of 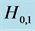
Table 4. Results of of Chow’s test.
well controlled for this study. This is further supported by the low 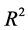
3. Macroeconomic Analysis of the Impact
As an input to almost all modern industries, the crude oil plays a critical role in today’s economy. Its promi- nence to the US market has soared in recent years. According to the data published by US Energy Information Administration, US exports of oil and petroleum products have increased by a factor of 3.6 from 2006 to 2015. On 12-18-2015, congress lifted a 40-year-old ban on crude oil export. Therefore, understanding the impact of recent oil price fluctuations to the economy as a whole is a topic of great importance.
Concerning the recent oil price shock, two widely used benchmarks were selected to measure its influence on the macroeconomy: GDP and CPI.
3.1. Impact of Oil Price Fluctuation on GDP
To examine the effect of the oil price fluctuations in the past two years on economy at a higher level, two linear models of average oil price on GDP growth rate were set up for the following countries: Japan, UK, USA, France, Germany, and Norway. More specifically, the models are:
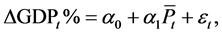
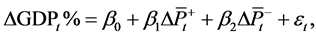
where 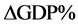
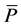
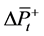
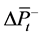
To counter the autocorrelations that are natural to the GDP data and that are introduced by the interpolation, the regressions were corrected with Heteroskedasticity and Autocorrelation Consistent (HAC) covariance estimation, followed [8] . Table 5 and Table 6 shows the result. The first table indicates that the estimators are significant when the selected country is a major oil producer (such as UK and Norway). This result is reasonable, as oil plays a vital role in these countries’growth. Nonetheless, the low R2s in both models suggest that they performed poorly, which in turn implies that oil prices cannot explain many variations in GDP. Two reasons may explain this observation. First, time lags may exist between the oil price fluctuations and their impact, so the change in oil price won’t be reflected on GDP instantly. Second, GDP often explains itself, i.e. it is highly autocorrelated, hence it is unlikely to undergo sudden increases or decreases as oil prices have.
3.2. Impact of Oil Price Fluctuation on CPI
This section investigated the relationship between Consumer Price Index (CPI) and changes in the crude oil prices. Again, two regression model were proposed. During the initial analysis, we noted that the first-order lag terms can improve the performance of the models, therefore they are included. Stepwise selection utilizing AIC was then applied on the model with lagged asymmetric price movements. Eventually the following models were chosen:
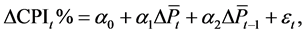
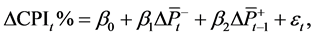
notations here are defined similarly as in Subsection 3.1. For this analysis, the US monthly CPI data in year 2013-2015 were collected from US Bureau of Labor Statistics, and monthly average oil prices were calculated based on WTI Cushing spot index. Concerning the potential bias of stepwise selection, as pointed out in [9] , LASSO was used on the model with asymmetric price movements, followed [10] . Incidentally, the simpler model (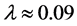
Table 5. Parameter estimates of model (3).
Table 6. Parameter estimates of model (4).
Table 7. Parameter estimates of model (5).
Table 8. Parameter estimates of model (6).
As mentioned above, the inclusion of the lag in the model significantly improves the model. One possible explanation for this behavior is that the effect of change in oil prices is not reflected immediately in CPI. Prices of many different goods and services, which are directly or indirectly related to the oil price changes, are included in the calculation of CPI. Some of the prices involved are relatively more sensitive to the oil price changes than others, so it will take some time before the impact of oil price fluctuations reaches each of them. Additionally, unlike crude oil prices which are continuously changing following the market dynamic, CPI is computed less frequently. Hence, the prices changes in the goods and services in the current period might only be seen in the next calculation of the CPI.
4. Conclusion
This paper examined the impact of the recent oil price shock; Subsection 2.1 provided a measure for the sensitivity of industry returns to change in oil price; Subsection 2.2 established a method to evaluate hedging effectiveness by analyzing the oil sensitivities of several airlines companies; in Section 3, the sensitivities of GDP and CPI with respect to oil price movement were analyzed. This paper found that the contemporary oil price change will affect the GDP of oil producing countries, but in general no strong link can be found. Finally, this paper concluded that the CPI is considerably affected by oil price change, and the reason is explicit since the oil price is indirectly involved in many parts of the CPI calculation.
Acknowledgements
The authors greatly appreciate the comments and suggestions from the editor-in-chief and anonymous reviewers which significantly improved the manuscript.
Cite this paper
Peng Xu,Utsav Adhikari,Lei Guo,Deepa Sathaye,Jihua Wang,Dongliang Yi,Yizhi Zhu, (2016) Quantifying the Microeconomic and Macroeconomic Impact of the Recent Crude Oil Price Fluctuations. Open Journal of Statistics,06,605-615. doi: 10.4236/ojs.2016.64051
References
- 1. Economist (2016) Who’s Afraid of Cheap Oil? Economist, 418, 9.
http://www.economist.com/news/leaders/21688854-low-energy-prices-ought-be-shot-arm-economy-think-again-whos-afraid-cheap - 2. Mork, K.A. (1989) Oil and the Macroeconomy When Prices Go Up and Down: An Extension of Hamilton’s Results. Journal of Political Economy, 97, 740.
http://dx.doi.org/10.1086/261625 - 3. Zhu, H.M., Guo, Y.W. and You, W.H. (2015) An Empirical Research of Crude Oil Price Changes and Stock Market in China: Evidence from the Structural Breaks and Quantile Regression. Applied Economics, 47, 6055-6074.
http://dx.doi.org/10.1080/00036846.2015.1064076 - 4. Christofi, A., Christofi, P. andAgacer, G. (2014) Oil Prices and U.S. Stock Prices. The International Journal of Finance, 26, 334-343.
- 5. Lewellen, J., Nagel, S. and Shanken, J. (2010) A Skeptical Appraisal of Asset Pricing Tests. Journal of Financial Economics, 96, 175-194.
http://dx.doi.org/10.1016/j.jfineco.2009.09.001 - 6. Clogg, C.C., Petkova, E. andHaritou, A. (1995) Statistical Methods for Comparing Regression Coefficients between Models. American Journal of Sociology, 100, 1261-1293.
http://dx.doi.org/10.1086/230638 - 7. Chow, G.C. (1960) Tests of Equality between Sets of Coefficients in Two Linear Regressions. Econometrica, 28, 591-605.
http://dx.doi.org/10.2307/1910133 - 8. Zeileis, A. (2004) Econometric Computing with HC and HAC Covariance Matrix Estimators. Journal of Statistical Software, 11, 1-17.
http://dx.doi.org/10.18637/jss.v011.i10 - 9. Steyerberg, E.W., Eijkemans, M.J.C. and Habbema. J.D.F. (1999) Stepwise Selection in Small Data Sets: A Simulation Study of Bias in Logistic Regression Analysis. Journal of Clinical Epidemiology, 52, 935-942.
http://dx.doi.org/10.1016/S0895-4356(99)00103-1 - 10. Friedman, J.H., Hastie, T. and Tibshirani. R. (2010) Regularization Paths for Generalized Linear Models via Coordinate Descent. Journal of Statistical Software, 33, 1-22.
http://dx.doi.org/10.18637/jss.v033.i01
Appendix
Table 1A. Parameters estimates for model (1).
Table 2A. Standard errors of estimates for model (1).
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/