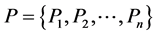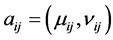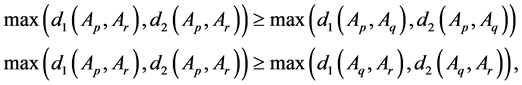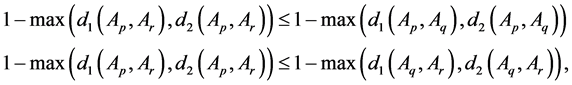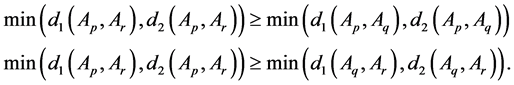Open Journal of Statistics
Vol.06 No.01(2016), Article ID:63437,6 pages
10.4236/ojs.2016.61005
A New Definition of Intuitionistic Fuzzy Similarity Degree
Qun Liu*, Changhuan Feng
College of Mathematics and Information, China West Normal University, Nanchong, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 December 2015; accepted 13 February 2016; published 16 February 2016
ABSTRACT
As far as the problem of intuitionistic fuzzy cluster analysis is concerned, this paper proposes a new formula of similarity degree with attribute weight of each index. We conduct a fuzzy cluster analysis based on the new intuitionistic fuzzy similarity matrix, which is constructed via this new weighted similarity degree method and can be transformed into a fuzzy similarity matrix. Moreover, an example is given to demonstrate the feasibility and validity of this method.
Keywords:
Intuitionistic Fuzzy Sets, Similarity Degree, Fuzzy Similarity Matrix, Clustering Analysis

1. Introduction
The fuzzy set theory has been widely used in various fields of modern society since it proposed by Zadeh [1] in the 1960s. The main idea of this theory is the extension from the characteristic function taking the value of 0 or 1 to the membership function which can take any value from the closed interval . However, in the increasingly complex socio-economic environment, there are different degrees of hesitation on comprehension and cognition, which can’t make a valid judgment. Therefore, the traditional fuzzy set cannot be used to completely describe all the information in such problems. Atanassov [2] expands Zadeh’s fuzzy set theory with the concept of intuitionistic fuzzy set (IFS), which is characterized by a membership function, a non-membership function and a hesitation function [3] . Since IFS can describe the uncertainty and the essence of fuzzy, it has been widely concerned and applied. The research on the application of intuitionistic fuzzy sets are mainly focused on the fields of multi-attribute decision making [4] [5] and pattern recognition [6] [7] . Many scholars have applied IFS to the cluster analysis, which generates the research of intuitionistic fuzzy cluster analysis (IFCA). At present, the research on the IFCA is still not perfect. In IFCA, the core of this problem is to obtain the proximity degree of two intuitionistic fuzzy vectors, which is the similarity degree in IFS. With the different forms, this paper discusses the problem of structuring similarity degree. Zhang [8] proposes an intuitionistic fuzzy similarity degree with an intuitionistic fuzzy number (IFN) and obtains the results by constructing intuitionistic fuzzy similarity matrix (IFSM), intuitionistic fuzzy equivalent matrix (IFEM) and l-cutting matrix of IFEM, while the similarity degree is not easy to calculate. Chen [9] proposes an intuitionistic fuzzy clustering method based on set valued statistics, and the similarity degree is represented by an IFN. The method is also complex in calculation.
. However, in the increasingly complex socio-economic environment, there are different degrees of hesitation on comprehension and cognition, which can’t make a valid judgment. Therefore, the traditional fuzzy set cannot be used to completely describe all the information in such problems. Atanassov [2] expands Zadeh’s fuzzy set theory with the concept of intuitionistic fuzzy set (IFS), which is characterized by a membership function, a non-membership function and a hesitation function [3] . Since IFS can describe the uncertainty and the essence of fuzzy, it has been widely concerned and applied. The research on the application of intuitionistic fuzzy sets are mainly focused on the fields of multi-attribute decision making [4] [5] and pattern recognition [6] [7] . Many scholars have applied IFS to the cluster analysis, which generates the research of intuitionistic fuzzy cluster analysis (IFCA). At present, the research on the IFCA is still not perfect. In IFCA, the core of this problem is to obtain the proximity degree of two intuitionistic fuzzy vectors, which is the similarity degree in IFS. With the different forms, this paper discusses the problem of structuring similarity degree. Zhang [8] proposes an intuitionistic fuzzy similarity degree with an intuitionistic fuzzy number (IFN) and obtains the results by constructing intuitionistic fuzzy similarity matrix (IFSM), intuitionistic fuzzy equivalent matrix (IFEM) and l-cutting matrix of IFEM, while the similarity degree is not easy to calculate. Chen [9] proposes an intuitionistic fuzzy clustering method based on set valued statistics, and the similarity degree is represented by an IFN. The method is also complex in calculation.
This paper constructs a new similarity degree that is based on the distance of the membership degree, non- membership degree and hesitation degree. Then, considering the risk factors [10] , the matrix is transformed from the IFSM with membership degree and non-membership degree to fuzzy similarity matrix with only membership degree. The advantage of this method is that the calculation is simple and it is easily operated. The attribute weights of each index are considered, which make the formula more scientific and reasonable. The correctness of the method is proved in theory, and the validity is demonstrated by an example.
2. Intuitionistic Fuzzy Set Theory
Definition 1 [3] . An IFS is an object having the following form:
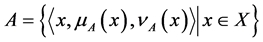
which is characterized by a membership function:
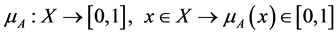
and a non-membership function:
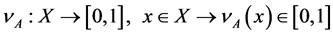 ,
,
with the condition:
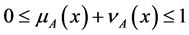 , for all
, for all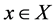 ,
,
where 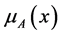 and
and 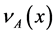 are called a membership degree and a non-membership degree of x in A.
are called a membership degree and a non-membership degree of x in A.
Moreover, for each IFS A in X, if
 , for all
, for all 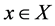
then  is called an hesitation degree of x to A. Obviously,
is called an hesitation degree of x to A. Obviously,
 , for all
, for all .
.
In particular, if
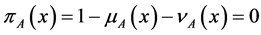 , for all
, for all 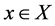
then A reduces to Zadeh’s fuzzy set. Thus, fuzzy sets are the special cases of IFSs.
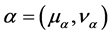
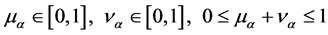
Let 
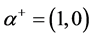
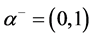
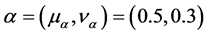
Atanassov proposed the inclusion relationship of two IFSs [3] .
Let 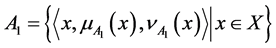
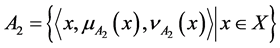
(1)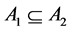
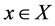
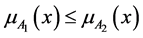
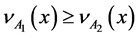
(2)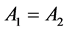
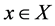
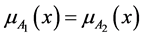
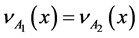
Definition 2 [3] . Let 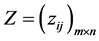
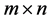
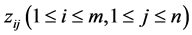
Definition 3 [8] . If 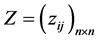
(1) Reflexivity: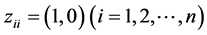
(2) Symmetry: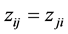
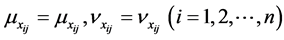
Definition 4 [9] . Let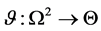
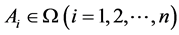
If 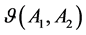
(1) 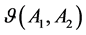
(2) 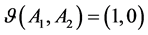
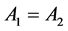
(3)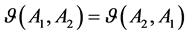
(4) If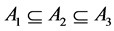
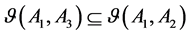
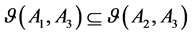
Then, 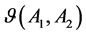
3. Fuzzy Clustering Analysis Based on IFSM
In the problem of multi-attribute decision making, 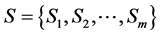
is an attribute set. The 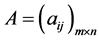
is the attribute value of scheme 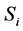
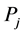
ation results. Let 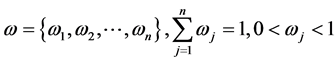
The attribute values of scheme 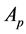
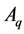
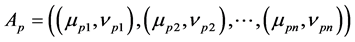
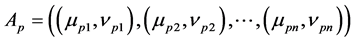
For convenience, the membership degree distance and non-membership degree distance between 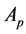
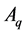
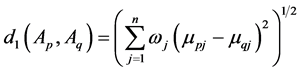
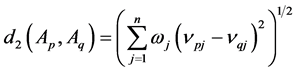
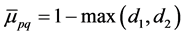
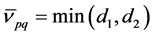
Theorem 1. Let 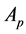
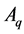
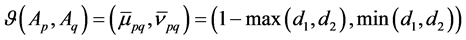
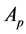
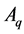
Proof: According to the 4 conditions in Definition 4, the process of this proof are as follows:
(1) Since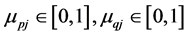
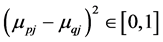
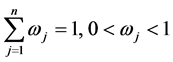
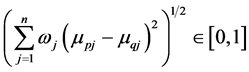
Hence, we have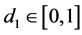

Thus, 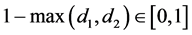
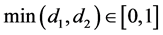
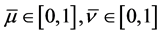
Since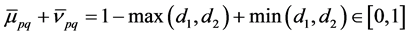
Therefore, 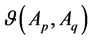
(2) When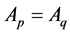
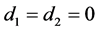
Therefore, we get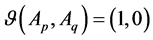
(3) Since 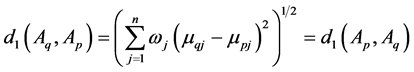
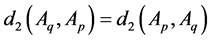
Thus, we have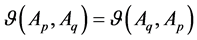
(4) If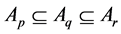
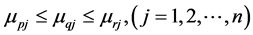
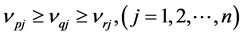
And since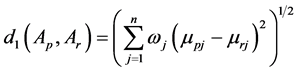
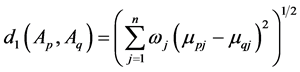
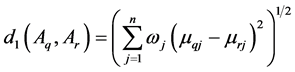
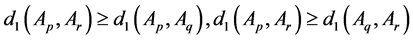
Similarly, we can obtain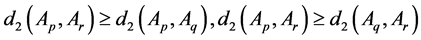
Thus,
i.e.,
and
Hence, we have 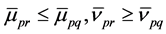
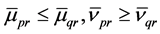
Thus, we can get 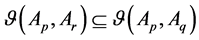
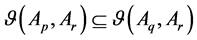
To sum up, the proof is completed.
Therefore, the intuitionistic fuzzy similarity degree between two schemes can be obtained by the Theorem 1, which can get the IFSM 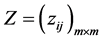
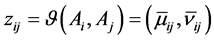
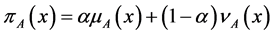
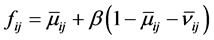
there into, 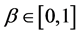
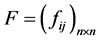
4. Empirical Analysis
In this paper, we select a case from Literature [8] , which is that a car market wants to classify the five kinds of different vehicles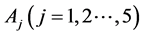
Table 1. Characteristic information for each car.
4.1. Constructing Intuitionistic Fuzzy Similarity Matrix
In the problem of multi-attribute decision making, the evaluation results are impacted by each attribute index on different extent, so it is necessary to give a reasonable weight coefficient for each index. The weights of the six evaluation factors are obtained via the intuitionistic fuzzy entropy calculating the weights’ method proposed by Szmidt Eulalia [11] . The weight of each index is 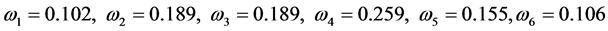
By the formula of Theorem 1, we can get a five orders IFSM with five different vehicles between each pair of similarity degree:
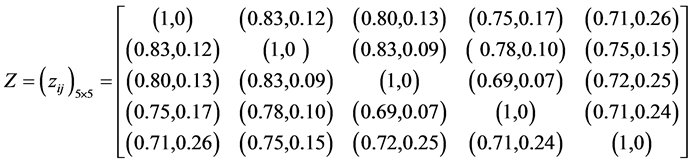
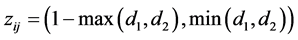
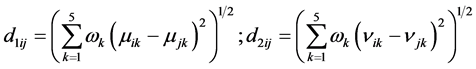
4.2. Fuzzy Clustering Analysis Based on IFSM
In order to make the IFCA more convenient, the value of similarity degree is transformed from IFN to fuzzy numbervia Equation (1):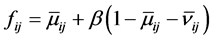
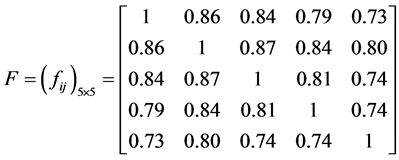
The results of the fuzzy clustering analysis through maximal tree method are shown in Figure 1.
The results of clustering analysis are as follows:
Cutting off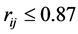
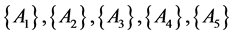
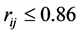
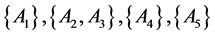
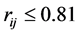
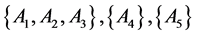
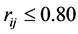
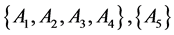
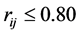
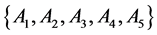
From the above results, it is clear that the clustering method proposed in this paper and the literature [10] are based on the intuitionistic fuzzy similarity formula, and the clustering results are represented for intuitionistic fuzzy similarity matrix. Although there are some differences in the corresponding values, the trend of elements in the matrix is same. The final clustering results are roughly the same as that of the literature [10] , which shows that the new similarity degree is effective. But the method proposed in this paper is more comprehensive and reasonable than the method in literature [8] , and it is simpler and easier to operate than the method in literature [10] .
Figure 1. The maximum tree cluster map.
4.3. Evaluation
To sum up, we can see that the new similarity degree proposed in this paper is correct and effective, and it has the following advantages:
(1) With the form of IFN, the information of the data is fully extracted;
(2) Taking into account the weight of the index attribute, the calculation results are more reasonable;
(3) The new similarity degree takes into account the membership degree and the non-membership degree, and it fully extracts the information provided by the intuitionistic fuzzy numbers;
(4) Computational process is simple and easy to operate.
5. Conclusion
This paper proposes a new method to compute intuitionistic fuzzy similarity degree. The formula is not only considered with the weight of each index attribute but also expressed by an IFN. It makes the information fully extracted. Meanwhile, the computational process is simple and convenient. Considering the risk factor, we obtain IFSM through the new similarity degree. Then, the IFSM is converted to a fuzzy similarity matrix. Finally, we get the result of cluster analysis through the method of maximum tree. In this paper, we prove the correctness of the new similarity degree and illustrate the validity and rationality of the method with an example. This method extends the research space of the intuitionistic fuzzy similarity degree.
Funding
Supported by China West Normal University special funding for basic scientific research business expenses (no.14C004), Social Science Programming general Program of Nan Chong city (no.NC2013B027).
Cite this paper
QunLiu,ChanghuanFeng, (2016) A New Definition of Intuitionistic Fuzzy Similarity Degree. Open Journal of Statistics,06,31-36. doi: 10.4236/ojs.2016.61005
References
- 1. Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, No. 8, 338-353.
http://dx.doi.org/10.1016/S0019-9958(65)90241-X - 2. Atanassov, K.T. (1986) Intuitionistic fuzzy Sets. Fuzzy Sets and Systems, 20, 87-96.
http://dx.doi.org/10.1016/S0165-0114(86)80034-3 - 3. Xu, Z.S. (2008) The Theory and Application of Intuitionistic Fuzzy Information Integration. Science Press, Beijing, 1-2.
- 4. Li, D.F. (2011) The GOWA Operator Based Approach to Multi-Attribute Decision Making Using Intuitionistic Fuzzy Sets. Mathematical and Computer Modeling, 53, 1182-1196.
http://dx.doi.org/10.1016/j.mcm.2010.11.088 - 5. Dymova, L.D. and Sevastjanov, P. (2010) An Interpretation of Intuitionistic Fuzzy Sets in Terms of Evidence Theory: Decision Making Aspect. Knowledge-Based Systems, 23, 772-782.
http://dx.doi.org/10.1016/j.knosys.2010.04.014 - 6. Guo, X.Z. and Li, J. (2009) Similarity Measure and Distance Measure of Intuitionistic Fuzzy Sets. Fuzzy Systems and Mathematics, 23, 124-130.
- 7. Xu, Z.S. (2007) On Similarity Measures of Interval-Valued Intuitionistic Fuzzy Sets and Their Application to Pattern Recognition. Journal of Southeast University, 23, 139-143. (In English)
- 8. Zhang, H.M., Xu, Z.S. and Chen, Q. (2007) Research on Clustering Method of Intuitionistic Fuzzy Sets. Control and Decision Making, 22, 882-888.
- 9. Chen, X.M. and Yao, Z.Q. (2011) Intuitionistic Fuzzy Clustering Based on Set Valued Statistics. Fuzzy Systems and Mathematics, 25, 100-108.
- 10. Li, P., Liu, S.F. and Zhu, J.J. (2013) Clustering Method Based on New Intuitionistic Fuzzy Similarity. Control and Decision Making, No. 28, 758-762.
- 11. Eulalia, S. and Kacprzyk, J. (2001) Entropy for Intuitionistic Fuzzy Sets. Fuzzy Sets and Systems, 118, 467-477.
http://dx.doi.org/10.1016/S0165-0114(98)00402-3
NOTES
*Corresponding author.