Open Journal of Statistics
Vol.05 No.03(2015), Article ID:56016,9 pages
10.4236/ojs.2015.53024
A Unified Approach for the Multivariate Analysis of Contingency Tables
Carles M. Cuadras1, Daniel Cuadras2
1Department of Statistics, University of Barcelona, Barcelona, Spain
2Statistical Service, Sant Joan de Deu Research Foundation, Barcelona, Spain
Email: cmcuadras@gmail.com, danicuadras@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 January 2015; accepted 22 April 2015; published 28 April 2015
ABSTRACT
We present a unified approach to describing and linking several methods for representing categorical data in a contingency table. These methods include: correspondence analysis, Hellinger distance analysis, the log-ratio alternative, which is appropriate for compositional data, and the non-symmetrical correspondence analysis. We also present two solutions working with cummulative frequencies.
Keywords:
Correspondence Analysis, Hellinger Distance, Log-Ratio Analysis, Generalized Pearson Contingency Coefficient, Correspondence Analysis with Cumulative Frequencies

1. Introduction
In multivariate analysis, it is usual to link several methods in a closed expression, which depends on a set of parameters. Thus, in cluster analysis, some criteria (single linkage, complete linkage, median), can be unified by using parametric coefficients. The biplot analysis on a centered matrix , is based on the singular value de- composition (SVD)
, is based on the singular value de- composition (SVD)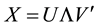 . The general solution is
. The general solution is 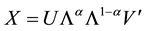 with
with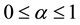 , providing the GH, JK, SQ and other biplot types depending on
, providing the GH, JK, SQ and other biplot types depending on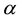 . Also, some orthogonal rotations in factor analysis (varimax, quartimax) are particular cases of an expression depending on one or two parameters.
. Also, some orthogonal rotations in factor analysis (varimax, quartimax) are particular cases of an expression depending on one or two parameters.
There are several methods for visualizing the rows and columns of a contingency table. These methods can be linked by using parameters and some well-known matrices. This parametric approach shows that correspon- dence analysis (CA), Hellinger distance analysis (HD), non-symmetric correspondence analysis (NSCA) and log-ratio analysis (LR), are particular cases of a general expression. In these methods, the decomposition of the inertia is used as well as a generalized version of Pearson contingency coefficient. With the help of triangular matrices, it is also possible to perform two analyses, Taguchi’s analysis (TA) and double accumulative analysis (DA), both based on cumulative frequencies. This paper unifies and extends some results by Cuadras and Green- acre [1] -[4] .
2. Weighted Metric Scaling
A common problem in data analysis consists in displaying several objects as points in Euclidean space of low dimension.
Let  be a set with
be a set with 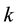 objects,
objects,  a distance function on
a distance function on 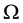 providing the
providing the  Eu- clidean distance matrix
Eu- clidean distance matrix , where
, where 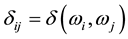 Let
Let 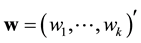 a weight vector such that
a weight vector such that 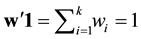 with
with  and
and  the column vector of ones.
the column vector of ones.
The weighted metric scaling (WMS) solution using 

where 








The 










The geometric variability of 


The geometric variability (also called inertia) can be interpreted as a generalized variance [6] .
If 








We should use the first m columns of 





3. Parametric Analysis of Contingency Tables
Let 











where 











A suitable choice of 
With this transformation, let us consider the following SVD depending on three parameters:

where 







However, different weights are used for the column representation, e.g.,

The first principal coordinates account for a relative high percentage of inertia, see Section 2. This parametric approach satisfies the principle of distributional equivalence and has been explored by Cuadras and Cuadras [2] and Greenacre [4] . Here we use Greenacre’s parametrization.
The geometric variability for displaying rows, is the average of the distances weighted by the row marginal frequencies:

where 

For measuring the dispersion in model (2), let us introduce the generalized Pearson contingency coefficient

Note that 


The unified approach for all methods (centered and uncentered) discussed below, are given in Table 1. It is worth noting that, from

the centered 

To give a WMS approach compatible with (1), we mainly consider generalized versions without right-
centering, i.e., post-multiplying 

Table 1. Four methods for representing rows and columns in a contingency table.
graph of rows without applying this post-multiplication. To do this compute the SVD 





4. Testing Independence
Suppose that the rows and columns of 












vergence is in law.
To prove this asymptotic result, suppose 



But



If 


5. Correspondence Analysis
In this and the following sections, we present several methods of representation, distinguishing, when it is necessary, the centered from the uncentered solution. The inertia is given by the geometric variability and the generalized Pearson coefficient, respectively.
Centered and Uncentered

1) Chi-square distance between rows:
2) Rows and columns coordinates:
3) Inertia:
Some authors considered CA the most rational method for analyzing contingency tables, because its ability to display in a meaningful way the relationships between the categories of two variable [8] -[10] . For the history of CA, see [11] , and for a continuous extension, see [12] [13] . CA can be understood as the first order approxima- tion to the alternatives HD and LR given below [3] . Besides, LR would be a limiting case of parametric CA [14] .
6. Hellinger Distance Analysis
Centered
1) Hellinger distance between rows:
2) Rows and columns coordinates:
3) Inertia:

Although the distances between rows are the same, the principal coordinates in the centered and uncentered
solutions are distinct. Note that 

HD is suitable when we are comparing several multinomial populations and the column profiles should not have influence on the distance. See [15] [16] .
7. Non-Symmetric Correspondence Analysis
Centered and Uncentered

1) Distance between rows:
2) Rows and columns coordinates:
3) Inertia:
Note that 


The numerator of 
8. Log-Ratio Analysis
Centered
1) Log-ratio distance between rows:
2) Rows and columns coordinates:

3) Inertia:

In spite of having the same distances, the principal coordinates (centered and uncentered) are different. Note that
The inertia and the geometric variability in these four methods, as well as Taguchi’s method given in Section 2, are summarized in Table 2. For a comparison between CA, HD, and LR see [3] [21] . Besides, by varying the parameters there is the possibility of a dynamic presentation linking these methods [22] .
9. Double-Centered Log-Ratio Analysis
In LR analysis Lewi [23] and Greenacre [4] considered the weighted double-centered solution

called “spectral map”. The unweighted double-centered solution, called “variation diagram”, was considered by Aitchison and Greenacre [20] . They show that log-ratio and centered log-ratio biplots are equivalent. In this solution the role of rows and columns is symmetric.
10. Analysis Based on Cumulative Frequencies
Let 





and cumulative column proportions

The Taguchi’s statistic [24] , is given by

Table 2. Inertia expressions for five methods for representing rows in contingency tables. In CA and NSCA the geometric variability coincides with the contingency coefficient. This coefficient does not apply in TA.
where 


on 
The so-called Taguchi’s inertia 
By using 


then 




As it occurs in CA, where the inertia is the trace 



From (4), centering is not necessary here




1) Distance between rows:
2) Rows and columns coordinates:

3) Inertia:

where
There is a formal analogy between 






11. Double Acumulative Frequencies
More generally, the analysis of a contingency table 

where 



Finally, from

all (uncentered) methods CA, HD, NSCA, LR, TA and DA can be unified by means of the SVD

as it is reported in Table 3. If



12. An Example
The data in Table 4 is well known. This table combines the hair and eye colour of 5383 individuals. We present the first two principal coordinates (centered solution) of the five hair colour categories for CA, HD, LR and NSCA. We multiply the NSCA solution (denoted by
These four solutions are similar.
Finally, we show the first two coordinates for Taguchi’s and double accumulative solutions
Table 3. Correspondence analysis, Hellinger analysis, non-symmetric correspondence analysis, log-ratio analysis and two solutions based on cumulative frequencies. The right column suggests the type of categorical data.
Table 4. Classification of a large sample of people combining the hair colour and the eye colour.

Both solutions are quite distinct from the previous ones.
References
- Cuadras, C.M. (2002) Correspondence Analysis and Diagonal Expansions in Terms of Distribution Functions. Journal of Statistical Planning and Inference, 103, 137-150. http://dx.doi.org/10.1016/S0378-3758(01)00216-6
- Cuadras, C.M. and Cuadras, D. (2006) A Parametric Approach to Correspondence Analysis. Linear Algebra and its Applications, 417, 64-74. http://dx.doi.org/10.1016/j.laa.2005.10.029
- Cuadras, C.M., Cuadras, D. and Greenacre, M. (2006) A Comparison of Different Methods for Representing Categorical Data. Communications in Statistics-Simulation and Computation, 35, 447-459. http://dx.doi.org/10.1080/03610910600591875
- Greenacre, M. (2009) Power Transformations in Correspondence Analysis. Computational Statistics and Data Analysis, 53, 3107-3116. http://dx.doi.org/10.1016/j.csda.2008.09.001
- Cuadras, C.M. and Fortiana, J. (1996) Weighted Continuous Metric Scaling. In: Gupta, A.K. and Girko, V.L., Eds., Multidimensional Statistical Analysis and Theory of Random Matrices, VSP, The Netherlands, 27-40.
- Cuadras, C.M., Fortiana, J. and Oliva, F. (1997) The Proximity of an Individual to a Population with Applications in Discriminant Analysis. Journal of Classification, 14, 117-136. http://dx.doi.org/10.1007/s003579900006
- Goodman, L.A. (1993) Correspondence Analysis, Association Analysis, and Generalized Nonindependence Analysis of Contingency Tables: Saturated and Unsaturated Models, and Appropriate Graphical Displays. In: Cuadras, C.M. and Rao, C.R., Eds., Multivariate Analysis: Future Directions 2, Elsevier, Amsterdam, 265-294.
- Beh, E.J. (2004) Simple Correspondence Analysis: A Bibliographic Review. International Statistical Review, 72, 257-284.
- Benzecri, J.-P. (1976) L’Analyse des Donnees. II. L’Analyse des Correspondances. Deuxieme Edition. Dunod, Paris.
- Greenacre, M.J. (1984) Theory and Applications of Correspondence Analysis. Academic Press, London. http://www.carme-n.org/?sec=books5
- Lebart, L. and Saporta, G. (2014) Historical Elements of Correspondence Analysis and Multiple Correspondence Analysis. In: Blasius, J. and Greenacre, M., Eds., Visualization and Verbalization of Data, CRC Press, Taylor & Francis Group, New York, 31-44.
- Cuadras, C.M., Fortiana, J. and Greenacre, M. (2000) Continuous Extensions of Matrix Formulations in Correspondence Analysis, with Applications to the FGM Family of Distributions. In: Heijmans, R.D.H., Pollock, D.S.G. and Satorra, A., Eds., Innovations in Multivariate Statistical Analysis, Kluwer Academic Publishers, Dordrecht, 101-116. http://dx.doi.org/10.1007/978-1-4615-4603-0_7
- Cuadras, C.M. (2014) Nonlinear Principal and Canonical Directions from Continuous Extensions of Multidimensional Scaling. Open Journal of Statistics, 4, 132-149. http://dx.doi.org/10.4236/ojs.2014.42015
- Greenacre, M. (2010) Log-Ratio Analysis Is a Limiting Case of Correspondence Analysis. Mathematical Geosciences, 42, 129-134. http://dx.doi.org/10.1007/s11004-008-9212-2
- Domenges, D. and Volle, M. (1979) Analyse Factorielle Spherique: Une Exploration. Annales de L’INSEE, 35, 3-84.
- Rao, C.R. (1995) A Review of Canonical Coordinates and an Alternative to Correspondence Analysis Using Hellinger Distance. Questiio, 19, 23-63.
- Beh, E.J. and D’Ambra, L. (2009) Some Interpretative Tools for Non-Symmetrical Correspondence Analysis. Journal of Classification, 26, 55-76. http://dx.doi.org/10.1007/s00357-009-9025-0
- Kroonenberg, P.M. and Lombardo, R. (1999) Nonsymmetric Correspondence Analysis: A Tool for Analyzing Contingency Tables with a Dependence Structure. Multivariate Behavioral Research, 34, 367-396. http://dx.doi.org/10.1207/S15327906MBR3403_4
- Lauro, N. and D’Ambra, L. (1984) L’analyse non symetrique des correspondances. In: Diday, E., Jambu, M., Lebart, L., Pages, J. and Tomassone, R., Eds., Data Analysis and Informatics III, North Holland, Amsterdam, 433-446.
- Aitchison, J. and Greenacre, M. (2002) Biplots of Compositional Data. Applied Statistics, 51, 375-392. http://dx.doi.org/10.1111/1467-9876.00275
- Greenacre, M. and Lewi, P. (2009) Distributional Equivalence and Subcompositional Coherence in the Analysis of Contingency Tables, Ratio-Scale Measurements and Compositional Data. Journal of Classification, 26, 29-54. http://dx.doi.org/10.1007/s00357-009-9027-y
- Greenacre, M. (2008) Dynamic Graphics of Parametrically Linked Multivariate Methods Used in Compositional Data Analysis. Universitat Pompeu Fabra, Barcelona. http://www.econ.upf.edu/en/research/onepaper.php?id=1082
- Lewi, P.J. (1976) Spectral Mapping, a Technique for Classifying Biological Activity Profiles of Chemical Compounds. Arzneimittel Forschung―Drug Research, 26, 1295-1300.
- Taguchi, G. (1974) A New Statistical Analysis for Clinical Data, the Accumulating Analysis in Contrast with the Chi-Square Test. Saishin Igaku (The New Medicine), 20, 806-813.
- Nair, V.N. (1987) Chi-Square Type Tests for Ordered Categories in Contingency Tables. Journal of the American Statistical Association, 82, 283-291. http://dx.doi.org/10.1080/01621459.1987.10478431
- Beh, E.J., D’Ambra, L. and Simonetti, B. (2011) Correspondence Analysis of Cumulative Frequencies Using a Decomposition of Taguchi’s Statistic. Communications in Statistics-Theory and Methods, 40, 1620-1632. http://dx.doi.org/10.1080/03610921003615880












