Open Journal of Statistics
Vol.05 No.01(2015), Article ID:53677,10 pages
10.4236/ojs.2015.51005
Implicit Hypotheses Are Hidden Power Droppers in Family-Based Association Studies of Secondary Outcomes
Jean Gaschignard1,2*, Quentin B. Vincent1,2, Jean-Philippe Jaïs1,2,3, Aurélie Cobat1,2, Alexandre Alcaïs1,2,4
1Laboratoire de Génétique des Maladies Infectieuses, Institut National de la Santé et de la Recherche Médicale, Paris, France
2Université Paris Descartes, Sorbonne Paris Cité, Institut Imagine, Paris, France
3Biostatistique et Informatique Médicale, Hôpital Necker, Paris, Farnce
4URC, CIC, Necker and Cochin Hospitals, Paris, France
Email: *jean.gaschignard@inserm.fr, alexandre.alcais@inserm.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 January 2015; accepted 26 January 2015; published 30 January 2015
ABSTRACT
Family-based tests of association between a genetic marker and a disease constitute a common design to dissect the genetic architecture of complex traits. The FBAT software is one of the most popular tools to perform such studies. However, researchers are also often interested in the genetic contribution to a more specific manifestation of the phenotype (e.g. severe vs. non-severe form) known as a secondary outcome. Here, what we demonstrate is the limited power of the classical formulation of the FBAT statistic to detect the effect of genetic variants that influence a secondary outcome, in particular when these variants also impact on the onset of the disease, the primary outcome. We prove that this loss of power is driven by an implicit hypothesis, and we propose a derivation of the original FBAT statistic, free from this implicit hypothesis. Finally, we demonstrate analytically that our new statistic is robust and more powerful than FBAT for the detection of association between a genetic variant and a secondary outcome.
Keywords:
Family-Based Association Test, FBAT, Genetic Association Studies, Null Hypothesis, Secondary Outcome, Homogeneity Test

1. Introduction
The aim of genetic epidemiological studies is to identify the genetic factors influencing the development of common diseases. Genetic epidemiology combines classical epidemiological data (assessment of risk factors known to affect the expression of the phenotype studied) and genetic information (familial relationships, typing of genetic marker) and proposes a large range of tools to address the initial question, the use of one depending on the nature of your sample and the size of your wallet. Over the past ten years, however, our understanding of the pattern of genetic variation at the genome scale, coupled to an unprecedented decrease in the cost of measuring this variation, has put (genome-wide) association studies at the front. Although the vast majority of genetic association study designs are derived from usual case-control retrospective epidemiological studies (i.e. that compare the distribution of allelic/genotypic frequencies between a group of cases and a group of controls), one is quite specific to the field of genetic epidemiology and relies on the collection and analysis of families. Such family-based tests of association between a genetic item (allele, genotype...) and the disease under study offer interesting features as compared to case-control designs (Laird and Lange [1] ; Chen and Abecasis [2] ). They are robust against population stratification, allow the inference of both haplotype phase and missing genotypes (Chen and Abecasis [2] ; Burdick et al. [3] ), and can identify peculiar allelic segregation, for example, due to imprinting effect (Vincent et al. [4] ).
The Transmission Desequilibrium Test (TDT) has emerged as the first popular family-based test of associa- tion (Spielman et al. [5] ). It tests whether the transmission of a given allele from a heterozygote parent to an affected child is different from what is expected in the absence of any association between the genetic marker and the disease under study. The null hypothesis is written as p = 0.5 where p is the proportion of a given allele that has been transmitted to affected children by heterozygote parents. Whereas the TDT could only analyze binary traits in samples of pure trios (i.e. two parents and a single affected child), Laird et al. [6] proposed a more comprehensive approach designed to handle binary, quantitative or censored traits, multiple genetic models (e.g. additive, dominant or recessive) and more complex family structures (e.g. families with multiple children). This approach uses a natural measure of association between two variables, i.e. the covariance between phenotypes and genotypes, and relies on a score-test. It has been implemented in the popular Family Based Association Test software (FBAT, Laird et al. [6] ; Rabinowitz and Laird [7] ; Lange and Laird [8] ). In this context of familial samples, FBAT has proved very efficient in identifying alleles associated with many phenotypes, whether binary or quantitative (e.g. Mira et al. [9] ; Cobat et al. [10] ).
Although developed to handle a large variety of tests according to the nature of both the traits and their genetic determinants, it is intrinsically designed to test primary outcomes (e.g. affected vs. unaffected) as the null hypothesis is based on the same underlying principles as the TDT (i.e. p = 0.5). However, in many cases researchers are interested in the genetic contribution to a more specific phenotype (e.g. severe vs. non-severe form), here denoted as a secondary outcome. Here, what we demonstrate is the limited power of the classical formulation of the FBAT statistic to detect the effect of genetic variants that influence a secondary outcome, in particular when these variants also impact on the onset of the disease, the primary outcome. We prove that this loss of power is driven by an implicit hypothesis and we propose a derivation of the original FBAT statistic, free from this implicit hypothesis. Finally, we demonstrate analytically that our new statistic is robust and more powerful than FBAT for the detection of association between a genetic variant and a secondary outcome.
2. Original FBAT Statistic
For sake of simplicity and without major loss of generality, we consider the analysis of a diallelic marker in a sample of trios with no missing parental data under an additive genetic model. Using the same notations as in the original FBAT paper (Laird et al. [6] ),
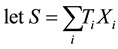
in which
 represents the genotype at the locus being tested and
represents the genotype at the locus being tested and
 the phenotype of the child of family
the phenotype of the child of family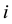 . The expectation of
. The expectation of
 is calculated conditioned on the parental genotypes under the null hypothesis of no association.
is calculated conditioned on the parental genotypes under the null hypothesis of no association.
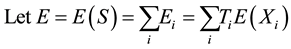
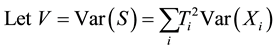
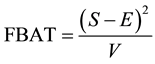
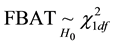
Under an additive model,
 is the number of copy of the allele under study (0, 1 or 2). As the most common way to code the phenotype is
is the number of copy of the allele under study (0, 1 or 2). As the most common way to code the phenotype is
 for affected individuals and
for affected individuals and
 for unaffected ones. In a sample with no missing parental data, unaffected individuals do not contribute to the statistic; however, in the presence of missing parental data, such unaffected individuals will indirectly impact on the statistic as they can be used to infer missing parental genotypes under some conditions (Knapp [11] ). S is generally written as:
for unaffected ones. In a sample with no missing parental data, unaffected individuals do not contribute to the statistic; however, in the presence of missing parental data, such unaffected individuals will indirectly impact on the statistic as they can be used to infer missing parental genotypes under some conditions (Knapp [11] ). S is generally written as:
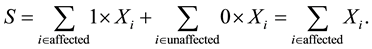
The null hypothesis of no association between the phenotype and a given allele is the random transmission of this allele from heterozygote parents to (affected) children. By noting
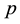 the transmission probability of this allele, the null
the transmission probability of this allele, the null
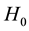 and alternate
and alternate
 hypotheses can be written as:
hypotheses can be written as:
The tested allele will be considered “at risk” or “protective” for the disease, if


3. FBAT Statistic to Test Secondary Outcomes
It is common practice to study a “primary” phenotype (e.g. disease yes/no) but as stated in the introduction, researchers are often interested in the genetic contribution to a “secondary” phenotype (e.g. severe vs. non-severe form of the disease). At first glance, FBAT could be used to test this hypothesis by computing the original statistic independently in the two modalities of the secondary outcome (e.g. severe and non-severe). Denoting


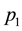



However, because of the bivariate nature of the phenotype under study (i.e. disease AND severe form or disease AND non-severe form), rejection of the null hypothesis cannot distinguish between alleles associated with the disease per se (i.e. independently of its severity) or alleles specifically associated with the severity of the disease. FBAT offers no immediate solution to study such secondary outcomes, i.e. to distinguish between alleles impacting the primary (e.g. disease per se) or the secondary (e.g. severe vs. non-severe) outcome. Below we propose two new tests denoted as FBAThet and FBAThet free that can be used to directly assess the association between a marker allele and a secondary outcome.
3.1. The FBAThet Test
A first straightforward idea is to perform a homogeneity test of the allelic transmission rate between the two subgroups


FBAThet = FBAT with the phenotypes coded as


 and
and : the software then calculates, for each allele, an offset
: the software then calculates, for each allele, an offset
 used to transform the phenotypic values in
used to transform the phenotypic values in
 and
and
 that minimizes the variance of the statistics. We show in Appendix B that using the offset option is equivalent to coding
that minimizes the variance of the statistics. We show in Appendix B that using the offset option is equivalent to coding
 and
and , thus testing for secondary outcome. Here, one should not code unaffected individuals as 0 but as missing to avoid that the controls interfere in the calculation of the statistics. FBAT software can be downloaded from: http://www.biostat.harvard.edu/fbat/fbat.htm.
, thus testing for secondary outcome. Here, one should not code unaffected individuals as 0 but as missing to avoid that the controls interfere in the calculation of the statistics. FBAT software can be downloaded from: http://www.biostat.harvard.edu/fbat/fbat.htm.
Indeed,
The two hypotheses can then be written as:
Note that under an additive genetic model and in a sample of trios with no missing parental data, coding






of heterozygote parents of children with phenotype


3.2. The FBAThet free Test
A somewhat hidden/under evaluated constraint of FBAThet is that the null hypothesis forces the transmission probabilities in both groups to be 0.5. Although valid and likely efficient in quite a number of practical situations, this can dramatically impact the power of the test in the study of a secondary outcome. A simple example being that carrying one copy of the allele is sufficient to develop the disease per se but that carrying two alleles will be associated with developing a severe form of the disease.
We propose a new statistic denoted as FBAThet free that relaxes this 0.5 constraint. Consider a diallelic locus (A and



their children with phenotype



from



Whereas in the above-mentioned FBAT and FBAThet tests the expected transmission of the allele of interest
under the null hypothesis of no association is 0.5, in FBAThet free it is


for FBAT, FBAThet and FBAThet free. The contribution to
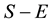





and variance of a trio including two heterozygote parents are twice those of a trio with only one heterozygote
parent. Symmetrically,








It is shown in Appendix C that FBAThet free is a Pearson’s chi-squared test. In summary, the hypotheses of the FBAThet free test can be written as:
As opposed to FBAT and FBAThet, the implicit/hidden 0.5 constraint has disappeared.
3.3. Comparison of FBAThet and FBAThet free
To illustrate the magnitude of the differential power of FBAThet and FBAThet free, we could have gone for large simulation studies. However, we show analytically in Appendix D that:
Figure 1. Contribution of a trio to FBAT, FBAThet and FBAThet free according to the number of heterozygote parents. In a trio with one (left panel) and two (right panel) heterozygote parents, the expected genotypes aa, Aa and AA of the child will vary according to the statistics used. In FBAT and FBAThet, the transmission probability of an allele A from an heterozygote parent is



The distribution of ρ according to

with an affected child (150


sion of allele A is 0.7 in







When there is an equivalent number of transmissions of alleles
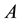


to their children,


Figure 2. Distribution of











4. Discussion
Family-based association studies have gained popularity to dissect the genetic architecture of complex traits and FBAT is likely the most popular tool to perform such studies. We have shown that at first glance it can be conveniently used to test for secondary outcomes, e.g. genetic heterogeneity between severe and non-severe forms of a disease. As an example, in a sample of trios, one can weight each “sub-phenotype” (severe and non-severe) by the inverse of the variance of each statistic. We called this test FBAThet, for which the null and
alternative hypotheses are



However, in the previous test, the transmission probabilities under the null hypothesis are fixed to 0.5 in both groups. This may not be optimal in the context of secondary outcomes when the transmission of the tested allele has already been found to significantly differ from 0.5 with respect to the primary outcome. We show that it is possible to relax this constraint by modifying the expectation in the FBAThet statistic so that the test is defined as



For sake of simplicity, we have derived our main statistic FBAThet free in the context of the analysis of a diallelic marker under an additive genetic model in a sample of trios with no missing parental data. However, generalization to other genetic models and more complex family structures should be possible by using, for a given marker, the estimated mean transmission of the allele under study among affected individuals, in preference to the actual 0.5 that prevents testing
Acknowledgements
We thank Laurent Abel, Jean-Laurent Casanova and all members of the Epidemiological Group for their support
Figure 3. Power of FBAThet vs. FBAThet free according to the mean transmission rate of the tested allele among the affected children.
and constructive criticism. JG is funded by the Fondation pour la Recherche Médicale, and QV by the Institut Imagine. This work was supported by the Programme Blanc de l’Agence National de la Recherche.
References
- Laird, N.M. and Lange, C. (2006) Family-Based Designs in the Age of Large-Scale Gene-Association Studies. Nature Reviews Genetics, 7, 385-394. http://dx.doi.org/10.1038/nrg1839
- Chen, W.M. and Abecasis, G.R. (2007) Family-Based Association Tests for Genomewide Association Scans. American Journal of Human Genetics, 81, 913-926. http://dx.doi.org/10.1086/521580
- Burdick, J.T., Chen, W.M., Abecasis, G.R. and Cheung, V.G. (2006) In Silico Methods for Inferring Genotypes in Pedigrees. Nature Genetics, 38, 1002-1004. http://dx.doi.org/10.1038/ng1863
- Vincent, Q., Alcais, A., Alter, A., Schurr, E. and Abel, L. (2006) Quantifying Genomic Imprinting in the Presence of Linkage. Biometrics, 62, 1071-1080. http://dx.doi.org/10.1111/j.1541-0420.2006.00610.x
- Spielman, R.S., McGinnis, R.E. and Ewens, W.J. (1993) Transmission Test for Linkage Disequilibrium: The Insulin Gene Region and Insulin-Dependent Diabetes Mellitus (IDDM). American Journal of Human Genetics, 52, 506-516.
- Laird, N.M., Horvath, S. and Xu, X. (2000) Implementing a Unified Approach to Family-Based Tests of Association. Genetic Epidemiology, 19, S36-S42. http://dx.doi.org/10.1002/1098-2272(2000)19:1+<::AID-GEPI6>3.0.CO;2-M
- Rabinowitz, D. and Laird, N. (2000) A Unified Approach to Adjusting Association Tests for Population Admixture with Arbitrary Pedigree Structure and Arbitrary Missing Marker Information. Human Heredity, 50, 211-223. http://dx.doi.org/10.1159/000022918
- Lange, C. and Laird, N.M. (2002) Power Calculations for a General Class of Family-Based Association Tests: Dichotomous Traits. American Journal of Human Genetics, 71, 575-584. http://dx.doi.org/10.1086/342406
- Mira, M.T., Alcais, A., Van Thuc, N., Moraes, M.O., Di Flumeri, C., Hong Thai, V., Chi Phuong, M., Thu Huong, N., Ngoc Ba, N., Xuan Khoa, P., et al. (2004) Susceptibility to Leprosy Is Associated with PARK2 and PACRG. Nature, 427, 636-640. http://dx.doi.org/10.1038/nature02326
- Cobat, A., Gallant, C.J., Simkin, L., Black, G.F., Stanley, K., Hughes, J., Doherty, T.M., Hanekom, W.A., Eley, B., Jais, J.P., et al. (2009) Two Loci Control Tuberculin Skin Test Reactivity in an Area Hyperendemic for Tuberculosis. Journal of Experimental Medicine, 206, 2583-2591. http://dx.doi.org/10.1084/jem.20090892
- Knapp, M. (1999) The Transmission/Disequilibrium Test and Parental-Genotype Reconstruction: The Reconstruction- Combined Transmission/Disequilibrium Test. American Journal of Human Genetics, 64, 861-870. http://dx.doi.org/10.1086/302285
Appendix A. Proof That Coding




Let


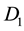







Let


For FBAT and FBAThet,


Given that




For FBAThet free,


Then coding




Appendix B. Proof That

Let

With the same notations as in Appendix A,
For FBAT,


and

For FBAThet free,


and

Appendix C. Proof That FBAThet free Is a Pearson’s
With the notations of the manuscript, let us write the table of contingency of the transmission of alleles A and a in two phenotypic groups.
Appendix D. Proof That FBATfree = ρFBAThet free
With the notations used in the main text, for FBAThet ,
with
NOTES
*Corresponding author.
1More precisely, in the general case, the null hypothesis of FBAT is “no association OR no linkage” and therefore the alternate hypothesis is “association AND linkage”. H0 can be written as a composite hypothesis: “no association AND no linkage” ∪ “no association AND linkage” ∪ “association AND no linkage”. In the particular case of a sample limited to trios, there is no linkage information, and the hypotheses are: H0 = association, H1 = no association.
2FBAThet can be implemented in FBAT by using the offset option “-o” while coding











































