Received 8 September 2014; revised 6 October 2014; accepted 2 November 2014

ABSTRACT

Theoretical results related to properties of a regularized recursive algorithm for estimation of a high dimensional vector of parameters are presented and proved. The recursive character of the procedure is proposed to overcome the difficulties with high dimension of the observation vector in computation of a statistical regularized estimator. As to deal with high dimension of the vector of unknown parameters, the regularization is introduced by specifying a priori non-negative covariance structure for the vector of estimated parameters. Numerical example with Monte-Carlo simulation for a low-dimensional system as well as the state/parameter estimation in a very high dimensional oceanic model is presented to demonstrate the efficiency of the proposed approach.

Keywords:

Linear Model, Regularization, Recursive Algorithm, Non-Negative Covariance Structure, Eigenvalue Decomposition

1. Introduction

In [1] a statistical regularized estimator is proposed for an optimal linear estimator of unknown vector in a linear model with arbitrary non-negative covariance structure

(1)

where 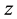is the p-vector observation, 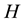is the 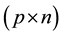observation matrix, 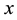is the n-vector of unknown parameters to be estimated, 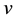is the p-vector representing the observation error.

It is assumed

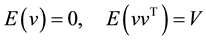(2)

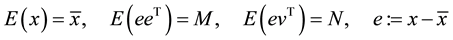(3)

where 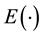is the mathematical expectation operator. Throughout this paper let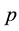, 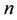be any positive inte-

gers, the covariance matrix of the joint vector 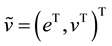may be singular (and hence the model (1)-(3) is called a linear model with arbitrary non-negative covariance structure).

No particular assumption is made regarding the probability density function of 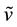and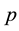, 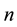are any positive integers.

In [1] the optimal linear estimator for the unknown vector 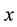in the model (1)-(3) is defined as

(4)

where is the transpose of, denotes the pseudo-inversion of .

As in practice all the matrices and the observation vector are given only approximately, instead of data set we are given their -approximations

(5)

hence the resulting estimate.

As shown in [1] , there are situations when the error between the “true” estimate and its perturbed may be very large even for small data error. The regularization procedure has been proposed in [1] to overcome this difficulty.

In this paper we are interested in obtaining a simple recursive algorithm for computation of subject to the situation when or or/and, may be very high.

This problem is very important for many practical applications. As example, consider data assimilation problems in meteorology and oceanography [2] . For typical data set in oceanography, at each assimilation instant we have the observation vector with,. Under such conditions it is unimaginable to compute the estimate (4) using standard numerical methods. We will show that there exists a simple algorithm to overcome these difficulties by exploiting a recursive character of the algorithm with an appropriate regularization in the form of the priori covariance matrix for the vector of unknown parameters.

2. Simple Recursive Method for Estimating the Vector of Parameters

2.1. Problem Statement: Free-Noise Observations

First consider the model (1) and assume that. We have then the system of linear equations

(6)

and for the noise-free observations.

Suppose that the system (6) is compatible, i.e. there exists such that. In what follows let

, , i.e. is the component of, is the row-vector of.

The problem is to obtain a simple recursive procedure to compute a solution of the system (6) when the dimension of is very high.

2.2. Iterative Procedure

To find a solution to Equation (6), let us introduce the following system of recursive equations

(7a)

(7b)

(7c)

Mention that the system is compatible if where is a linear space spanned by the columns of. Throughout of the paper, for definiteness, let,.

Theorem 1. Suppose the system (6) is compatible. Then for any finite and symmetric positive definitive (SPD) matrix we have.

In order to prove Theorem 1 we need

Lemma 1. The following equalities hold

(8)

Proof. By induction. We have for,

since.

Let the statement be true for some. We show now that it is true also for. As the statement is true for, it implies,. We have to prove

Substituting into, taking into account the form of one sees that as, it implies, (End of Proof).

Lemma 2. The following equalities hold

(9)

Proof. By induction. We have for,. As, it is evident that.

Let the statement be true for some. We show now that it is true also for. As the statement is true for, it implies,. We have to prove,. From the definition of,

However from Lemma 1, as, for all. (End of Proof).

Proof of Theorem 1.

Theorem follows from Lemma 2 since under the conditions of Theorem, from Equation (9) for it follows, or. (End of Proof).

Corollary 1. Suppose the rows of are linearly independent. Then under conditions of Theorem 1,.

Proof. By induction. The fact that for, implies at least the null subspace of has one nonzero element hence. We show now that it is impossible that.

Suppose that, For simplicity, let. It means that there exist linearly independent vectors such that any element from the subspace can be represented on the basis of these elements. As to the matrix

its subspace has the dimension 1 hence any element from can be represented on the basis of some vector. Thus any element from the subspace with can be represented as a linear combination of elements. On the other hand, as is non-singular, any element of must be represented as a linear combination of linearly independent vectors. It contradicts the fact that any element from could be written as a linear combination of linearly

independent elements. We conclude that it is impossible hence. The same argument is true for.

Suppose now Corollary is true for and we have to prove that it holds for. For

we have,. From Lemma 1 it follows, hence the null subspace has the dimension (as all the rows of are linearly independent). It follows that the dimension of the subspace is at least less or equal to.

By the same way as proved for one can show that it is impossible hence (End of Proof).

Comment 1. By verifying the rank of, Corollary 1 allows us to check if the computer code is correct. In particular if is non-singular, at the end of the iterative procedure the matrix should be zero. The recursive Equations (7a)-(7c) then yield the unique solution of the equation after iterations.

Using the result (8) in Lemma 1, it is easy to see that:

Corollary 2. Suppose is linearly dependent on. Then in (7),.

Corollary 3. Suppose are linearly independent, is linearly dependent on. Then under the conditions of Theorem 1,

Corollary 3 follows from the fact that when is linearly dependent on from Corollary 2, and hence by Corollary 1,.

Comment 2. Equation (7c) for is similar to that given in (3.14.1) in [3] since from Corollary 2 it follows automatically if is linearly dependent on. Their difference is that in (7c) the initial may be any SPD matrix whereas in (3.14.1) of [3] it is assumed.

In the next section we shall show that the fact may be any SPD matrix is important to obtain the optimal in mean squared estimator for.

3. Optimal Properties of the Solution of (7)

3.1. Regularized Estimate

Theorem 1 says only that Equations (7a)-(7c) give a solution to (1). We are going now to study the question on whether a solution of Equations (7a)-(7c) is optimal, and if yes, in what sense? Return to Equations (1)-(3) and assume that,. The optimal estimator (4) is then given in the form

(10)

where is the pseudo-inversion of. Consider first the equation. In this case, (10) yields the optimal estimator (obtained on the basis of the first observation)

(11a)

and one can prove also that the mean square error for is equal to

(11b)

If we apply Equation (3.14.1) in [3] , then instead of we have

(12)

For simplicity, let. Comparing Equation (12) with Equation (11) shows that if is the orthogonal projection of onto the subspace spanned by, the estimate belongs to the subspace spanned by. Thus the algorithm (11) takes into account the fact that we known a priori belongs to the space. This fact is very important when the number of observations is much less than the number of the estimated parameters as it happens in oceanic data assimilation: today usually,.

In [4] a similar question has been studied which concerns the choice of adequate structure for the Error Covariance Matrix (ECM).

We prove now a more strong result saying that all the estimates, are projected onto the space.

Theorem 2. Consider the algorithm (7). Suppose. Then all the estimates, belong to the space spanned by the columns of, i.e..

Proof. For the statement is evident as shown above.

Suppose the statement is true for some. We will show that it is true also for.

Really as, it is sufficient to show that From, , as it follows that. But hence the columns of must belong to. Again from the equation for in Equation (7) we have. It proves since (End of proof).

Theorem 2 says that by specifying the algorithm (7) will produce the estimates belonging to the subspace. Specification of the priori matrix plays the most important task if we want the algorithm (7) to produce the estimate with high quality.

Comment 3

1) If does not belong to, by considering in place of Theorem 3 remains valid for the algorithm (7) written for. In this case at the first iteration, as represents the priori error for, it is natural for the algorithm to seek the correction (i.e., the estimate for the error) belonging to the space. In what follows, unless otherwise stated, for simplicity we assume.

2) Theorem 2 says that there is a possibility to regularize the estimate when the number of observations is less than the number of estimated parameters by choosing. Thus the algorithm can be considered as that which finds the solution under the constraint. In the procedure in Albert (1972) putting means that there is no constraint on hence the best way to do is to project orthogonally onto subspace of.

3.2. Minimal Variance Estimate

Suppose is a random variable having the mean and covariance matrix. We have then the following result.

Theorem 3. Suppose is a random variable having the mean and the covariance matrix. Then generated by the recursive Equation (7) is an unbiased and minimum variance estimate for in the class of all unbiased estimates linearly dependent on and.

Proof. Introduce for the system (6),

(13)

and the class of all estimates linearly dependent on and.

The condition for unbiasedness of is

or

from which follows. Substituting this relation into leads to

(14)

It means that all the estimate in Equation (14) is unbiased.

Consider the minimization problem

We have

Taking the derivative of with respect to implies the following equation for finding,

from which follows one of the solutions

If now instead of Equation (13) we consider the system

(15)

and repeat the same proof, one can show that the unbiased minimum variance estimate for is given by

(16a)

(16b)

Using the properties of the pseudo-inverse (Theorem 3.8 [3] ), one can prove that

(17)

Thus for a very small the estimate is unbiased minimum variance which can be made as close as possible to.

On the other hand, applying Lemma 1 in [5] for the case of uncorrelated sequence, one can show that

, (18a)

, (18b)

(18c)

(18d)

Letting one comes to in (7) (End of proof).

3.3. Noisy Observations

The algorithm (18a)-(18d) thus yields an unbiased minimal variance (UMV) estimates for in the situation when represents the observation noise variance. We want to stress that these algorithms produce the UMV estimates only if where is the true covariance of the error before arriving,.

3.4. Very High Dimension of: Simplified Algorithms

In the field of data assimilation in meteorology and oceanography usually the state vector is of very high dimension, the orders of [2] . This happens because is a collection of several variables defined in the three dimensional grid. If the algorithm (7) allows to overcome the difficulties with the high dimension of the observation vector (each iteration involves one component of), due to high dimension of , it is impossible to handle Equation (7c) to evaluate the matrices (with the number of elements). This section is devoted to the question on how one can overcome such difficulties.

Let us consider the eigen-decomposition for [6]

(19)

In (19) the columns of are the eigenvectors of and is diagonal with the elements at the diagonal?the eigen-values of. Let,. If we put in the algorithms (7) or (18), then the algorithm (7), for example, will yield the best estimate for projected in the subspace. Let has the dimension,. Let

.

3.4.1. Main Theoretical Results

Theorem 4

Consider two algorithms of the type (7) subject to two matrices

where the columns of consist of leading eigenvectors of,. Then the following inequalities hold

(20)

is the estimate produced by the algorithm (7) subject to, where the strict inequality takes place if.

Proof

Write the representation of in the terms of decomposition of on the basis of its eigenvectors (for simplicity, let),

(21)

where is of zero mean and has the covariance matrix.

Let is a sample of. Theorem 3 states that for all, the algorithm (7) will yield the estimate with the minimal variance.

In what follows we introduce the notation:

?the true ECM of;

?a truncated covariance coming from;

?the initialized ECM in the algorithm (7a)-(7c).

The samples of are coming from a variable having zero mean and covariance.

?sample coming from a variable having zero mean and covariance.

There are the following different cases

1): By Theorem 3 the algorithm (7) will produce the estimates of minimal variance for all; This is true also if Equation (7) is applied to.

2):

a) For samples belonging to: The estimates will be of minimal variance.

b) For samples belonging to (i.e. belonging to but not to): The estimates will not be of minimal variance.

Thus in the mean sense

(22)

3) Consider two initializations and, ,. In the same way we have

a):

i): the estimates are of minimal variance;

ii): the estimates are not of minimal variance.

b): The algorithm (7) will produce the estimates

i) of minimal variance for;

ii) of minimal variance for;

iii) not of minimal variance for.

Thus in the mean sense

(23)

3.4.2. Simplified Algorithm

Theorem 5

Consider the algorithm (7) subject to, ,.

Then this algorithm can be rewritten in the form

, (24a)

(24b)

, (24c)

(24d)

It is seen that in the algorithm (24a)-(24d), the estimate belongs to the linear space of dimension. In data assimilation, it happens that the dimension of may be very high but there is only some leading directions (leading eigenvectors of representing the directions of most rapid growth of estimation error) to be captured. Thus the algorithm (24a)-(24d) is quite adapted for solving such problems: first the initial covariance is constructed from physical considerations or numerical model, and next to decompose it (numerically) to obtain an approximated decomposition

Mention that the version (24a)-(24d) is very closed to that studied in [7] for ensuring a stability of the filter.

4. Numerical Example

Consider the system (1) subject to the covariance,

(25)

Here we assume that the 1st and 3rd components of is observed, i.e.

(26)

Numerical computation of eigendecomposition of yields

(27)

(28)

The algorithm (24a)-(24d) is applied subject to three covariance matrices,. They are denoted as ALG(m).

In Figure 1 we show the numerical results obtained from the Monte-Carlo simulation.

There are 100 samples simulating the true which are generated by a random generator distributed according to the normal distribution. The curves in Figure 1 represent rms of the estimation error obtained by different algorithms. Here the curves, , correspond to the three algorithms ALG(1), ALG(2), ALG(3).

The curve denotes the 4th algorithm ALG (4) which is run subject to?identity matrix. This is equivalent to the orthogonal projection (using the pseudo-inversion of) of into the subspace.

As seen from Figure 1, the estimation error is highest in ALG (1). There is practically no difference between ALG (2) and ALG (3) which are capable of decreasing considerably the estimation error (50%) compared to ALG (1). As to the ALG (4), its performance is situated between ALG (1) and ALG (2). This experiment confirms the theoretical results and demonstrates that if we are given a good priori information on the estimated parameters, there exists a simple way to improve the quality of the estimate by appropriately introducing the priori information in the form of the regularization matrix.

The results produced by ALG (1) and ALG (4) show also that when the priori information is insufficiently rich, the algorithm naturally produces the estimates of poor quality. In such situation, simple applying orthogonal projection can yield a better result. For the present example, the reason is that using the 2nd mode allows to capture the important information contained in the second observation. Ignoring it (as does ALG (1)) is equivalent to ignoring the second observation. As to the third mode, it has a weak impact on the estimation since the corresponding eigenvalue is small. That explains why ALG (2) and ALG (3) have produced almost the same results.

5. Experiment with Oceanic MICOM Model

5.1. MICOM Model

In this section we will show importance of the regularization factor in the form of the priori covariance in the design of a filter for systems of very high dimension.

The numerical model used in this experiment is the MICOM (Miami Isopycnic Coordinate Ocean Model) which is exactly as that presented in [8] . We recall only that the model configuration is a domain situated in the North Atlantic from to and to. The grid spacing is about in longitude and in latitude, requiring the horizontal mesh;. The distance between two points,. The number of layers in the model. We note that the state of the model where is the thickness of the layer, , are two velocity components. The “true” ocean is simulated by running the model from “climatology” during two years. Each ten days the sea-surface height (SSH) are stored at the grid points; which are considered as observations in the assimilation experiment. The sequence of true states will be available and allows us to compute the estimation errors. Thus the observation operator is constant at all assimilation instants.

The assimilation experiment consists of using the SSH to correct the model solution, which is initialized by some arbitrarily chosen state resulting from the control run.

5.2. Different Filters

The different filters are implemented to estimate the oceanic circulation. It is well known that determining the filter gain is one of the most important tasks in the design of a filter. As for the considered problem it is impossible to apply the standard Kalman filter [9] since in the present experiment, and the number of elements in the ECM is of order. At each assimilation instant, the estimate for the system state in all filters is computed in the form (10) with the corresponding ECM. As the number of observations is largely inferior to the dimension of the system state, the choice of as a regularization factor has a great impact on the quality of the produced estimates. In this assimilation experiment the following filters will be employed. First the Prediction Error Filter (PEF) whose ECM is obtained on the basis of leading real Schur vectors [8] . Parallelly two other filters, one is the Cooper-Haines filter (CHF) [10] and another is an EnOI (Ensemble based Optimal Interpolation) filter [11] will be used. Mention that the ECM in the CHF is obtained on the basis of the principle of a vertical rearrangement of water parcels (see also [8] ). The method conserves the water masses and maintains geostrophy. The main difference between PEF and EnOI is lying in the way to generate the ensembles of Prediction Error (PE) samples. In the PEF, the ensemble of PE samples is generated using the sampling procedure described in [8] (and it will be denoted as En(PEF)). As for the EnOI, the ensemble of background errors samples (the term used in [8] ) and will be denoted by En(EnOI)) will be used. The elements of En(EnOI) are constructed according to the method in [11] . It consists of using 2-year mean of true states as the background field and the error samples are calculated as differences between individual 10-day true states during this period and the background.

According to Corollary 4.1 in [4] , using the hypothesis on separable vertical-horizontal structure for the ECM, we represent where, are the ECM of vertical and horizontal variables respectively. In the case of sea-surface height observations, from the representation, the gain filter can be represented in the form

where denotes the Kronecker product. The gain allows the correction available at the surface to propagate into all vertical subsurface layers. As to, it represents an operator of (horizontal) optimal interpolation which interpolates the observations over all horizontal grid points at the surface. Mention that the elements of and the correlation length parameter in are estimated by minimizing the mean distance between the data matrix and using a simultaneous perturbation stochastic approximation algorithm [12] . The data matrix is obtained from samples of the leading real Schur vectors as described in [8] .

Figure 2 shows the estimated vertical coefficients, obtained on the basis of the ECM spanned by the elements of En(PEF). It is seen that the estimates converge quite quickly. The estimated vertical gain coefficients computed on the basis of the ECM from two ensembles En(PEF), En(EnOI) at the iteration are

(29a)

(29b)

We remark that all the gain coefficients in two filters are of identical sign but the elements of are of much less magnitudes than that of. It means that the EnOI will make less correction (compared to the PEF) to the forecast estimate. Two gains in (29a), (29b) will be used in the two filters PEF and EnOI to assimilate the observations.

The vertical gain coefficients for the CHF are taken from [8] and are equal to

(30)

5.3. Numerical Results

In Figure 3 we show the instantaneous variances of the SSH innovation produced by three filters EnOI, CHF and PEF. It is seen that initialized by the same initial state, if the innovation variances in EnOI, CHF have a tendency to increase, this error remains stable for the PEF during all assimilation period. At the end of assimilation, the PE in the CHF is more than two times greater than that produced by the PEF. The EnOI has produced poor estimates, with error about two times greater than the CHF has done.

For the velocity estimates, the same tendency is observed as seen from Figure 4 for the surface velocity PE

errors. These results prove that the choice of ECM as a regularization factor on the basis of members of the En(PEF) allows to much better approach the true system state compared to that based on the samples taken from En(EnOI) or to that constructed on the basis of the physical consideration as in the CHF. The reason is that the members of En(PEF) by construction [8] are samples of the directions along which the prediction error increases most rapidly. In other words, the correction in the PEF is designed to capture the principal important components in the decomposion of the covariance of the prediction error.

6. Conclusion

We have presented some properties of an efficient recursive procedure for computation of a statistical regularized estimator for the optimal linear estimator in a linear model with arbitrary non-negative covariance structure. The main objective of this paper is to obtain an algorithm which allows overcoming the difficulties concerned with high dimensions of the observation vector as well as that of the estimated vector of parameters. As it was seen, the recursive nature of the proposed algorithm allows dealing with high dimension of the observation vector. By initialization of the associated matrix equation by a low rank approximation covariance which accounts for only first leading components of the eigenvalue decomposition of the priori covariance matrix, the proposed algorithm permits to reduce greatly the number of estimated parameters in the algorithm. The efficiency of the proposed recursive procedure has been demonstrated by numerical experiments, with the systems of small and very high dimension.

References