Open Journal of Statistics
Vol.04 No.09(2014), Article ID:50502,15 pages
10.4236/ojs.2014.49066
Confirmatory Methods, or Huge Samples, Are Required to Obtain Power for the Evaluation of Theories
Irene Klugkist1*, Laura Post1, Freek Haarhuis1, Floryt van Wesel2,3
1Department of Methodology and Statistics, Faculty of Social and Behavioural Sciences, Utrecht University, Utrecht, The Netherlands
2Department of Educational Neuroscience, Faculty of Psychology and Education, VU University Amsterdam, Amsterdam, The Netherlands
3Department of Methodology, Faculty of Psychology and Education, VU University Amsterdam, Amsterdam, The Netherlands
Email: *i.klugkist@uu.nl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 August 2014; revised 8 September 2014; accepted 16 September 2014
ABSTRACT
Experimental studies are usually designed with specific expectations about the results in mind. However, most researchers apply some form of omnibus test to test for any differences, with follow up tests like pairwise comparisons or simple effects analyses for further investigation of the effects. The power to find full support for the theory with such an exploratory approach which is usually based on multiple testing is, however, rather disappointing. With the simulations in this paper we showed that many of the common choices in hypothesis testing led to a severely underpowered form of theory evaluation. Furthermore, some less commonly used approaches were presented and a comparison of results in terms of power to find support for the theory was made. We concluded that confirmatory methods are required in the context of theory evaluation and that the scientific literature would benefit from a clearer distinction between confirmatory and exploratory findings. Also, we emphasis the importance of reporting all tests, significant or not, including the appropriate sample statistics like means and standard deviations. Another recommendation is related to the fact that researchers, when they discuss the conclusions of their own study, seem to underestimate the role of sampling variability. The execution of more replication studies in combination with proper reporting of all results provides insight in between study variability and the amount of chance findings.
Keywords:
Confirmatory Research, Exploratory Research, Power, Theory Evaluation

1. Introduction
Experimental studies are usually designed with specific expectations about the results in mind. Van den Hout and colleagues, for instance, designed a study to investigate differences in performance between interventions for posttraumatic stress disorder [1] . While it has been shown that Eye Movement Desensitization and Reprocessing (EMDR) is an effective treatment, recently, therapists sometimes replace eye movements (EMs) by alternating beep tones. To investigate if the intervention based on beep tones was: 1) effective at all, and 2) equally effective as the intervention using EMs, patients were randomized over three groups: recall only, recall with EMs, or recall with beep tones. Three competing expectations for the outcome were formulated:
H1: beep tones are as effective as EMs.
H2: beep tones are not effective at all.
H3: beep tones are effective, but not as effective as EMs.
In terms of the three conditions, this can also be expressed as:
H1: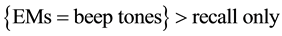 .
.
H2: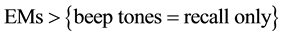 .
.
H3: .
.
The main goal of this experiment was to evaluate for which of these three competing hypotheses the data provided most support.
Another illustration of research with specific expectations about the results is presented by [2] . In a study on the effect of stereotype threats on the math performance of women and men, they hypothesized that on a relative simple math test there would be no differences in performance between men and women, but on a difficult test where they expected both men and women to perform worse than on the simple test, they did also expect men to score better than women. Let
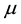 denote the mean performance and the subscripts w = women, m = men, s = simple and d = difficult. The expectations can be expressed as:
denote the mean performance and the subscripts w = women, m = men, s = simple and d = difficult. The expectations can be expressed as: .
.
This is an example of a factorial design but the hypothesis of interest is not formulated as, nor approached by, (default) testing for main or interaction effects, but instead expresses the specific theory of the researcher in one hypothesis.
Both examples show that research expectations are often expressed using order constraints on the model parameters (e.g. means in experimental groups). Hypotheses in terms of such constraints are denoted ordered, inequality constrained, or informative hypotheses [3] . We prefer the last term for two reasons. First, the hypothesis of interest can include order/inequality constraints (<, >), but also equality constraints (=) and unconstrained parts (denoted using a comma, e.g.
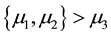 states that both
states that both
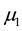 and
and
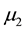 are greater than
are greater than , but there is no constraint with respect to the mutual relation of
, but there is no constraint with respect to the mutual relation of
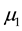 and
and ). Second, it emphasizes that the hypothesis is informative in the sense that it captures the information the researcher is interested in (i.e., the theory or explicit expectation).
). Second, it emphasizes that the hypothesis is informative in the sense that it captures the information the researcher is interested in (i.e., the theory or explicit expectation).
A review of empirical literature shows that many research articles contain such hypotheses, that is, in the introduction of the paper the authors clearly state what their expectations with respect to (part of) the outcomes are. This is especially the case in experimental studies. Despite such prespecified expectations or theories, most researchers apply some form of omnibus test to test for any differences, with follow up tests like pairwise comparisons or simple effects analyses for further investigation of the effects. The power to find full support for the theory with such an approach is, however, rather disappointing.
To illustrate this consider the hypothesis expressing the expectation that four means are of increasing magnitude, that is, the hypothesis states what is called a simple ordering of four means: .
.
After assuring that all assumptions to perform an analysis of variance (ANOVA) are met, we believe that the majority of researchers would approach this hypothesis by first testing the omnibus F-test to see if there is evidence for any differences between the four means. After rejection of the null hypothesis “all means equal”, one would probably investigate the pairwise comparisons to determine which means differ from each other. Throughout the paper,
 will be used to determine statistical significance.
will be used to determine statistical significance.
Full support for the theory could be claimed if 1) the omnibus F-test is statistically significant, 2) the sample means are in the hypothesized order, and 3) the pairwise comparisons testing ,
,
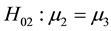 , and
, and
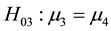 are statistically significant. Note that other approaches to decide on full support for Hinformative are available and several will be discussed and investigated in the next section.
are statistically significant. Note that other approaches to decide on full support for Hinformative are available and several will be discussed and investigated in the next section.
In a small simulation study, with population means in the hypothesized order, an effect size that can be labeled as medium (Cohen’s


From these numbers it is clear that the power for an omnibus ANOVA and the power to find support for a specific expectation about a pattern of means can deviate substantially. Similar results and conclusions were previously reported in [4] , although not in the context of testing informative (order constrained) hypotheses but in the general context of multiple testing. In [4] it was argued that multiple testing causes studies to be underpowered and that this leads to inconsistencies in the published literature. Multiple testing is also the main explanation for the low power in our illustration.
This paper has two main goals. We will show that many of the common choices in hypothesis testing lead to a severely underpowered form of theory evaluation. Furthermore, we will compare the results with available but less commonly used approaches and discuss when each of them could serve as a valuable and more powerful alternative.
In the next section six approaches are described that can be used in the context of a one-way ANOVA when the hypothesis of interest is a simple ordering of k means. For a variety of populations, two questions are investigated: “What is the power to find full support given that the power for the omnibus test is 80%?”, and “What is the required sample size to obtain 80% full support power for the specific expectations?”. In Section 3, the results are reported of simulation studies meant to investigate the specific interaction hypothesis in the two-way design of the math performance example just introduced. The paper is concluded with a discussion of results and possible implications for psychological research.
2. One-Way Analysis of Variance
In the context of a one-way ANOVA with k groups, six approaches are presented that researchers could employ when evaluating the explicit research hypothesis that the means are increasing, that is:

In Section 2.1, we present three approaches that are frequently seen in published research papers. However, these methods are not the best choice for theory evaluation, that is, for testing explicit hypotheses. Therefore, in Section 2.2, three alternative approaches are presented that may be better suited to evaluate pre-specified explicit hypotheses, but that are probably less familiar to some researchers. Sections 2.3, 2.4, and 2.5 present the results of several simulation studies.
2.1. Three Omnibus Test Based Approaches
The first three approaches are based on performing an omnibus ANOVA, despite the fact that the hypothesis of interest is more specific than the hypothesis evaluated with the omnibus test:




Additionally, to evaluate the actual research hypothesis (i.e., to be able to claim full support), three different follow-up procedures are considered.
I. Omnibus ANOVA + sample means in hypothesized order
To claim support for the research hypothesis, the omnibus test must be statistically significant (p < 0.05) and the sample means

II. Omnibus ANOVA + sample means in hypothesized order + all pairwise tests for subsequent means significantly different (with
If the omnibus test is significant (p < 0.05), researchers often continue with pairwise comparisons to further investigate which means differ significantly from each other. Full support for the hypothesis can only be claimed if all subsequent pairs of means (i.e.,






Since we are now applying multiple tests (each with


III. Omnibus ANOVA + sample means in hypothesized order + all pairwise tests for subsequent means significantly different (with Bonferonni corrected
In the third approach, the Bonferonni




2.2. Three Alternative Approaches
To do justice to the confirmatory nature of research, for

IV. Multiple planned contrasts (one-sided)
Planned contrast testing is an alternative to omnibus testing and can be used whenever pre-specified hypotheses are available (e.g., [6] ). In case of a simple order of





This provides, for example,



V. Linear contrast test (one-sided)
For hypotheses imposing a simple order on a sequence of means, the linear contrast is a close approximation. The linear contrast weights for
This provides, for example,















VI. Bayesian approach developed specifically for the evaluation of informative hypotheses
Another method that will be evaluated is a Bayesian procedure specifically designed for the evaluation of informative hypotheses (see, for instance, [3] and [7] ). With this model selection approach the support in the data for any hypothesis of interest is quantified with so-called Bayesian probabilities. Bayesian probabilities are numbers between zero and one reflecting the relative support for each hypothesis in a predefined set. In the simulation studies where the main interest is in a specific order constrained hypothesis, the set of models that will be compared consists of the null hypothesis


2.3. Simulation Studies
2.3.1. Defining the Populations
We investigated hypotheses expressing a simple ordering of








2.3.2. Power and Sample Sizes
From each population presented in Table 1, 10,000 data sets were sampled and subsequently analyzed with approaches I-V. The results for the Bayesian approach are based on 1000 data sets due to its intensive computation time. The sample sizes of the data sets are based on a power analysis using the following assumptions: 1) nowadays, it is more or less standard practice to start a research project with a power analysis to determine the number
Table 1. Population parameter values used for the simulation studies.
of required participants to obtain power of 0.80; 2) we expect that most researchers perform their power analysis for the omnibus test (i.e., for the one-way ANOVA) and that they do not take possible follow-up analyses and/or alpha corrections for multiple testing into account in the power analysis. Therefore, for each population, the required sample size to have 0.80 power for the omnibus ANOVA was determined and used in the simulations (numbers are reported in Table 2).
Additionally, for each of the six approaches, the approximate sample sizes required to obtain 0.80 full support power, as defined by the approach at hand and for the informative hypothesis of interest, are determined.
2.3.3. Results
In Table 2, the results for the six approaches are presented. The sample sizes used are provided in the first column and are based on a power analysis to obtain 0.80 power for the omnibus ANOVA. Note that all reported sample sizes are group sizes (

The results in column I show that, even if the only requirement is that the observed sample means should be in the hypothesized order, the power to find full support diminishes fast with an increasing number of means in the ordered hypothesis (approximately 0.70 for k = 3, 0.50 for k = 4, and 0.10 for k = 6). The power to find full support for the true order using the requirement that additional pairwise tests (one-sided or two-sided, and, with or without alpha corrections) should be significant reduces the power to zero in most cases (only for k = 3, full support power ranges between 0.02 - 0.15; see columns II-IV). Stated differently, with 10,000 replications from the same population, the true effect in the population was, with these methods, never fully confirmed.
The last two columns show that with the two confirmatory methods that do not rely on multiple tests, the power to find support for the ordered hypothesis is in almost all cases higher than the power of the omnibus test (ranging from 0.74 to 0.98). Further, it shows that for small effect sizes the linear contrast test has higher power than the Bayesian model selection approach, but that for medium and large effect sizes this is the other way around.
In Table 3, for the six approaches, the approximate required group sample sizes to obtain 0.80 full support power are provided. The numbers are obtained by running a sequence of simulations for each population (i.e., combination of


Table 2. Full support power for the six approaches for group sample sizes Nj that provide 0.80 power for the omnibus ANOVA (for several number of groups k and effect sizes ES).
*Sample sizes Nj that provide 0.80 power for the ANOVA were determined using Gpower 3.1 [11] .
Table 3. Approximate required group sample sizes Nj to obtain 0.80 full support power for each of the six approaches.
The results show that huge samples are required to have reasonable full support power to detect a small ES with any of the approaches I-IV (ranging from 360 to >1000 per group). Approach V is, for small ES, most powerful (


The required sample sizes to find full support for medium effect sizes vary greatly between the approaches as well as between different numbers of subgroups. For







Overall, the numbers in Table 2 and Table 3 clearly show that confirmatory methods that do not suffer from multiple testing issues (that is, approaches V and VI) are needed to have a good chance―with feasible sample sizes―to find full support for the true order of the means.
2.3.4. Additional Results for the Bayesian Approach
The Bayesian analysis for comparing










In Table 2, the reported proportions (the “power” of the Bayesian approach) were based on counting how often, in 1000 replications,



From Table 4, we can see that in 7% to 9% of the samples the null hypothesis is favored over the ordered hypothesis, leading to a wrong conclusion. Note that this information was also presented in Table 2, where the “power of the Bayesian approach” was defined as finding


2.3.5. Non-Linear True Effects
A hypothesis stating a simple ordering of means is not equal to a hypothesis stating a non-zero linear effect. It is interesting to see if the power of approach V also holds when the population means are ordered from small to large, but not linearly, and how this power compares to approach VI that explicitly states the expected order.
A small simulation study was performed for k = 3, 4, 6, with


The results show that the power of the Bayesian approach is higher for k = 3 and k = 4 and that the differences between approaches V and VI are largest for


3. An Illustration of a Two-Way Analysis of Variance
Often, ANOVA tests are done in the context of factorial designs, that is, with two or more factors and an interest in main and/or interaction effects. The example provided in the introduction will be used as an illustration. The researchers investigated stereotypes and gender differences in math performance in three subsequent studies [2] . In their first study, a group of highly selected respondents (see [2] for details) consisting of 28 men and 28 women, was randomized over easier and difficult math tasks. The goal of this study was to investigate if a specifically described expected interaction pattern was found. They formulated their expectation, for the studied population, as: “women underperform on difficult tests but perform just as well on easier test” ( [2] , page 9).
The hypothesized outcome, assuming general lower performance on the difficult test compared to the simple test, is represented in Figure 1. Formulated as an informative hypothesis, the expectation is:

The tests executed and reported in [2] , however, not directly address this expectation. They report F-tests for two main effects and an interaction effect (all p < 0.05), as well as posthoc pairwise comparisons of means. Therefore, multiple tests were required to come to the conclusion that, indeed, their expectation was supported.
A simulation study was designed to investigate the power to find full support for this specific expectation assuming different effect sizes and using several different approaches for the evaluation of the hypothesis. In Section 3.1 the approaches are presented and in Section 3.2 the design and results of the simulation study are provided.
Table 4. Proportions of different Bayes factors for k = 3, 4, 6 groups, medium effect size, and group sample sizes Nj providing power of 0.80 for the omnibus ANOVA.
Table 5. Comparison of the power of approaches V and VI when population means are increasing non-linearly.
Figure 1. Hypothesized results for the study on stereotypes and gender diffe- rences in mathematics [2] , with math performance on the y-axis.
3.1. Approaches
3.1.1. Factorial Approach
Most researchers would analyze these data with a two way ANOVA, testing for both main effects and the interaction effect. Different follow-up strategies could be considered, leading to three approaches described below. To limit the number of variations only results for two-sided tests and without alpha corrections are reported.
A. To conclude support for the theory, both main effects as well as the interaction effect should be statistically significant and the sample means




B. To conclude support for the theory, in approach B the three omnibus tests should be significant and the sample means in the right order (as in A) but also the simple main effects should support the theory. This implies finding a significant result for the test


C. Following [2] , as a follow-up to the requirements of approach A, we tested all pairwise comparisons of means. The results should be non-significant for
3.1.2. One Way Approach
Since the factorial approach is rather exploratory (testing for any main effect and any interaction and not for the specific, expected patterns), the omnibus tests could be skipped and instead planned comparisons on the four subgroup means could be executed and interpreted. Note that this implies ignoring the factorial structure in the design. Two approaches are included in the simulations:
D. The first approach is based on planned comparisons on specific contrasts. The ordering






E. The Bayesian approach for informative hypotheses can evaluate the expected pattern directly. In the simulation we will evaluate how often the informative hypothesis






3.2. Simulation Study and Results
For the simulation study, several populations were specified with means in agreement with the informative hypothesis of [2] . The residual variance was always one, and the differences between the means were increasing form relatively small to larger differences. The population means in five simulations are presented in Table 6. Results are also found in the table and are based on drawing 10,000 (1000 for approach E) samples with a sample size of 50 per group.
The results show, once again, that the power to find full support for a specific expectation dramatically decreases when several multiple tests are involved, as in approach A, B and―most of all―C. The power of approach D is already much higher. This can be explained by the fact that, here, only two tests were involved of which the first contrast specifically represents the order of interest and was evaluated with a one-sided

4. Discussion
Attention for limitations of null hypothesis testing in general, e.g., [13] - [15] , and problems with power, lack of replication, and multiple testing specifically, e.g., [4] [16] , is widespread in both statistical and applied research literature. In the past two decades, a Bayesian approach for the evaluation of informative hypothesis was presented as an alternative, confirmatory approach, e.g., [7] [17] [18] . In these papers it is often claimed that with the formulation and evaluation of informative hypotheses more powerful methods are obtained. In a few papers, some examples are provided to support this claim with numbers, e.g., [19] [20] . However, so far, no systematic study of the power of different―exploratory and confirmatory―approaches was reported and this is, therefore, the main contribution of this paper.
We presented several simulations in the context of evaluating a simple ordering of


Results in this paper show that the approaches that are mostly found in the research literature, that is, analysis of variance omnibus tests with multiple follow-up comparisons of means, have very limited power to detect the true pattern of means. Approaches that are specifically designed for the evaluation of prespecified expectations like planned contrast testing or the Bayesian approach for informative hypotheses do much better. Typical differences observed in the simulations for the one-way design were power levels between 0% - 15% for approaches based on multiple testing, whereas the power of the confirmatory approaches reached power levels between 80% - 100%.
Additional simulations were done to investigate what sample sizes would be needed to have reasonable power with the commonly used approaches. The main conclusion from these simulations is that it is practically unfeasible to detect the true pattern of means with such approaches if the effect size is small, and that it still requires huge group sample sizes to detect medium effects (

Table 6. Comparison of the power of approaches A-E when population means are in agreement with the hypothesis of interest with increasing differences between the means (Nj = 50).
The results lead to a couple of recommendations. First of all, if specific expectations are formulated beforehand, as is, for instance, often the case in psychological experiments like those described in the paper, we strongly recommend considering approaches that use as few multiple tests as possible. Planned contrasts have much more power to detect the true patterns than omnibus ANOVA’s with several follow-up tests, and so does the Bayesian approach. Whenever the expectation can be formulated in one contrast (e.g., the linear contrast we used in the one-way design to reflect the simple ordering of means), the differences in power between the contrast testing approach and the Bayesian approach are negligible for the effect sizes and numbers of groups investigated in this paper. A potential advantage of the Bayesian approach is flexibility in terms of the types of hypotheses that can be formulated and evaluated. Any expected pattern that can be expressed using a combination of smaller than (<), bigger than (>), equal to (=), and/or, no mutual constraint (,) can be evaluated using the Bayesian approach. An example where planned contrast testing required two tests and therefore resulted in less power to detect the true pattern than the Bayesian method was provided in the context of a factorial design and specific expectations about the interaction effect of the two factors.
The results of this paper also show how variable different samples from the same population can be. Although sampling variability is a concept known to all researchers that are familiar with data analysis and NHT, published literature shows that many researchers do often underestimate the size and consequences of sampling variability in their own study. Not finding a specific expected difference between two means, for instance, is often explained by substantive arguments. The fact that this could very likely be a type 2 error, due to limited power, is hardly ever mentioned, especially when some other interesting comparisons did reach statistical significance. Likewise, the finding of a significant difference between certain means that was not a priori expected often receives considerable attention. However, in the context of multiple testing the probability of finding at least one significant difference is large and therefore it might just as well be a chance finding (inflated type 1 error due to multiple testing). It seems that, significant and non-significant results are too often interpreted as rather certain indicators of the true effects. With this paper, we hope to contribute to the awareness that results from a single study can only provide conclusions with very limited certainty and that replication studies are crucial.
Another recommendation relates to the publication process, where a clearer distinction could be made between confirmatory and exploratory analyses. When specific theories or expectations are specified a priori and confirmatory methods are used to evaluate the expectations, conclusions can be relatively strong, although the need for replication studies will always remain. Other findings, or when no specific hypotheses were formulated, should be reported acknowledging the exploratory nature of the results. One can conclude that interesting findings were seen in this particular data set but replications with new data, and preferably confirmatory methods, are required before it can be concluded if they reflect real effects or chance findings.
5. Conclusion
The need for replication leads to a final recommendation, which is not at all original, but crucial to the accumulation of scientific knowledge. All results of all tests within a study should be properly reported, irrespective of their statistical significance, including the appropriate sample statistics (e.g. means, standard deviations, group sample sizes). This holds not only for non-significant findings within a study but also for studies where no significant results were found at all and that are currently often hard to get published. Only when these types of publication bias are avoided, replication studies can be properly synthesized and results judged for what they are worth. If such a publication culture could be established we can work towards accumulation of knowledge in a truly scientific way.
References
- Van den Hout, M.A., Rijkeboer, M.M., Engelhard, I.M., Klugkist, I., Hornsveld, H., Toffolo, M. and Cath, D.C. (2012) Tones Inferior to Eye Movements in the EMDR Treatment of PTSD. Behaviour Research and Therapy, 50, 275-279. http://dx.doi.org/10.1016/j.brat.2012.02.001
- Spencer, S.J., Steele, C.M. and Quinn, D.M. (1999) Stereotype Threat and Women’s Math Performance. Journal of Experimental Social Psychology, 35, 4-28. http://dx.doi.org/10.1006/jesp.1998.1373
- Hoijtink, H. (2012) Informative Hypotheses: Theory and Practice for Behavioral and Social Scientists. Chapman and Hall/CRC, London.
- Maxwell, S.E. (2004) The Persistence of Underpowered Studies in Psychological Research: Causes, Consequences, and Remedies. Psychological Methods, 9, 147-163. http://dx.doi.org/10.1037/1082-989X.9.2.147
- Williams, L.J. and Abdi, H. (2010) Fisher’s Least Significant Difference (LSD) Test. In: Salkind, N., Ed., Encyclopedia of Research Design, Sage, Thousand Oaks. http://dx.doi.org/10.4135/9781412961288.n154
- Rosenthal, R., Rosnow, R.L. and Rubin, D.B. (2000) Contrasts and Effect Sizes in Behavorial Research. A Correlation Approach. Cambridge University Press, Cambridge.
- Klugkist, I., Laudy, O. and Hoijtink, H. (2005) Inequality Constrained Analysis of Variance: A Bayesian Approach. Psychological Methods, 10, 477-493. http://dx.doi.org/10.1037/1082-989X.10.4.477
- Béland, S., Klugkist, I., Raîche, G. and Magis, D. (2012) A Short Introduction into Bayesian Evaluation of Informative Hypotheses as an Alternative to Exploratory Comparisons of Multiple Group Means. Tutorials in Quantitative Me- thods for Psychology, 8, 122-126.
- Klugkist, I., Van Wesel, F. and Bullens, J. (2011) Do We Know What We Test and Do We Test What We Want to Know? International Journal of Behavioral Development, 35, 550-560. http://dx.doi.org/10.1177/0165025411425873
- Van de Schoot, R., Mulder, J., Hoijtink, H., van Aken, M.A.G., Dubas, J.S., de Castro, B.O., Meeus, W. and Romeijn, J.-W. (2011) An Introduction to Bayesian Model Selection for Evaluating Informative Hypotheses. European Journal of Developmental Psychology, 8, 713-729. http://dx.doi.org/10.1080/17405629.2011.621799
- Faul, F., Erdfelder, E., Lang, A.G. and Buchner, A. (2007) G*Power 3: A Flexible Statistical Power Analysis Program for the Social, Behavioral, and Biomedical Sciences. Behavior Research Methods, 39, 175-191. http://dx.doi.org/10.3758/BF03193146
- Kass, R.E. and Raftery, A. (1995) Bayes Factors. Journal of the American Statistical Association, 90, 773-795. http://dx.doi.org/10.1080/01621459.1995.10476572
- Nickerson, R.S. (2000) Null Hypothesis Significance Testing: A Review of an Old and Continuing Controversy. Psychological Methods, 5, 241-301. http://dx.doi.org/10.1037/1082-989X.5.2.241
- Cohen, J. (1994) The Earth Is Round (p < .05). American Psychologist, 49, 997-1003. http://dx.doi.org/10.1037/0003-066X.49.12.997
- Royall, R.M. (1997) Statistical Evidence. A Likelihood Paradigm. Chapman & Hall, New York.
- Cumming, G. (2008) Replication and p Intervals: p Values Predict the Future Only Vaguely, but Confidence Intervals Do Much Better. Perspectives on Psychological Science, 3, 286-300. http://dx.doi.org/10.1111/j.1745-6924.2008.00079.x
- Mulder, J., Hoijtink, H. and Klugkist, I. (2010) Equality and Inequality Constrained Multivariate Linear Models: Objective Model Selection Using Constrained Posterior Priors. Journal of Statistical Planning and Inference, 140, 887- 906. http://dx.doi.org/10.1016/j.jspi.2009.09.022
- Van Wesel, F., Hoijtink, H. and Klugkist, I. (2010) Choosing Priors for Inequality Constrained Normal Linear Models: Methods Based on Training Samples. Scandinavian Journal of Statistics, 38, 666-690. http://onlinelibrary.wiley.com/doi/10.1111/j.1467-9469.2010.00719.x/full http://dx.doi.org/10.1111/j.1467-9469.2010.00719.x
- Kuiper, R.M. and Hoijtink, H. (2010) Comparisons of Means Using Exploratory and Confirmatory Approaches. Psychological Methods, 15, 69-86. http://dx.doi.org/10.1037/a0018720
- Van de Schoot, R., Hoijtink, H., Mulder, J., Van Aken, M.A.G., Orobio de Castro, B., Meeus, W. and Romeijn, J.W. (2011) Evaluating Expectations about Negative Emotional States of Aggressive Boys Using Bayesian Model Selection. Developmental Psychology, 47, 203-212. http://dx.doi.org/10.1037/a0020957
Appendix A: Tests Used in Approaches I-V (Section 2) and A-D (Section 3)
Notations used for one-way design:








Approach I
The ANOVA test result is determined using:
with:




and evaluated using the

Approaches II and III
The pairwise


and evaluated using the




Approach IV
Each planned contrast


and evaluated using the

Approach V
Denoting the linear contrast weight for



with:



and evaluated using the

Notations used for two-way design:














Approach A
The ANOVA test results are determined using:
with:








and evaluated using the

Approach B
Two t-tests are used for the simple main effects:

and evaluated using the

Approach C
All pairwise



and evaluated using the

Approach D
Denoting the contrast weights for


and evaluated using the



Appendix B: A Short Summary of the Bayesian Method in Approach VI (Section 2) and E (Section 3)
Note that this appendix was previously published as an appendix to the paper by Klugkist, Van Wesel, Bullens (2011).
Here, we will shortly outline the Bayesian approach applied in this paper for the analysis of variance (ANOVA) model:
where











The ANOVA model has the following likelihood:
where



Prior based on training data
The method and software used for the Bayesian analysis is based on Van Wesel, Hoijtink and Klugkist, (2011). In this paper, a thorough investigation of different priors that can be used for the analysis of informative hypotheses


where


The specification of the unconstrained prior


The general form of the ACPP is:
where


Posterior
The posterior distribution based on the ACPP is:
Bayes factors
The Bayes factor comparing two hypotheses is the ratio of two marginal likelihoods. A marginal likelihood, for instance

Subsequently, Klugkist and Hoijtink (2007) derived that in the context of encompassing priors (i.e., the constrained model is nested in the unconstrained), the Bayes factor comparing an informative hypothesis





Note that in this approach each





Posterior model probabilities
Using a uniform prior on the model space, the posterior model probabilities for



NOTES
*Corresponding author.













