Open Journal of Statistics
Vol.04 No.08(2014), Article ID:49942,13 pages
10.4236/ojs.2014.48056
Parameter Estimations for Some Modifications of the Weibull Distribution
Soumaya Ghnimi1, Soufiane Gasmi2
1Faculty of Sciences of Tunis, University of Tunis El Manar, Tunis, Tunisia
2Tunis National Higher School of Engineering, University of Tunis, Tunis, Tunisia
Email: soufiane.kasmi3@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 May 2014; revised 26 June 2014; accepted 12 July 2014
ABSTRACT
Proposed by the Swedish engineer and mathematician Ernst Hjalmar Waloddi Weibull (1887- 1979), the Weibull distribution is a probability distribution that is widely used to model lifetime data. Because of its flexibility, some modifications of the Weibull distribution have been made from several researches in order to best adjust the non-monotonic shapes. This paper gives a study on the performance of two specific modifications of the Weibull distribution which are the exponentiated Weibull distribution and the additive Weibull distribution.
Keywords:
Exponentiated Weibull Distribution, Additive Weibull Distribution, Maximum Likelihood Estimation, Kolmogorov-Smirnov Test, Simulation

1. Introduction
The Weibull distribution [1] is the most life-time probability distribution used in the reliability engineering discipline. Due to its wide applications [2] , many researchers have developed various extensions and modified forms of the Weibull distribution with a number of parameters ranging from 2 to 5. These distributions have several desirable properties and nice physical interpretations. The literature that studies the various modifications of the Weibull distributions is extensive, for example: the two-parameter flexible Weibull extension of Bebbington et al. [3] . Zhang and Xie [4] studied the characteristics and application of the truncated Weibull distribution which has a bathtub shaped hazard function.
A three-parameter model, called exponentiated Weibull distribution, was introduced by Mudholkar and Srivastave [5] . The modified Weibull distribution of Sarhan and Zaindin [6] was studied by Gasmi and Berzig [7] in the case of type I censored data. Another three-parameter model was developed by Marshall and Olkin [8] and is called the extended Weibull distribution. Xie et al. [9] proposed a three-parameter modified Weibull extension with a bathtub shaped hazard function. Lai et al. [10] have described the modified Weibull (MW) distribution. A four-parameter additive Weibull distribution (AddW) was proposed by Xie and Lai [11] . A second four-parameter beta Weibull distribution was proposed by Famoye et al. [12] . Cordeiro et al. [13] introduced another four-parameter distribution called the Kumaraswamy Weibull distribution. A five-parameter modified Weibull distribution was introduced by Phani [14] . The beta modified Weibull distribution was introduced by Silva et al. [15] and further studied by Cordeiro et al. [16] . Recently, an extensive review of some discrete and continuous versions of the modifications of the Weibull distribution was introduced by Almalki and Nadarajah [17] . The main objective of this article is in first step to estimate the three unknown parameters of the exponentiated Weibull distribution and the four unknown parameters of the additive Weibull distribution. Therefore, we use the maximum likelihood method to derive such estimates. In the second step, we study whether these distributions fit a set of real data of Aarset [18] better than other distributions. Two criteria are used for this purpose: the first one is the mean square distance MSD and the next one is the Kolmogorov-Smirnov test statistic. A real data set is analyzed and it is observed that the present distributions provide better fit than many existing well-known distributions. This paper will be organized as follows. In Section 2 we present the exponentiated Weibull distribution and the additive Weibull distribution. In Section 3, an application to real data is provided and different types of goodness-of-fit are applied to test the compatibility of the exponentiated Weibull distribution and the additive Weibull distribution in comparison to some other models. Mainly we use the mean square distance MSD and the Kolmogorov-Smirnov (K-S) test as a non-parametric test to illustrate how one can compare the exponentiated Weibull distribution and the additive Weibull distribution with some sub-models. Finally we conclude the paper in Section 4.
2. Parameter Estimates of EW and AddW Distributions
2.1. Exponentiated Weibull Distribution
The exponentiated Weibull (EW) distribution is proposed by Mudholkar and Srivastava [5] and studied first by Mudholkar et al. [19] and further by Mudholkar and Hutson [20] .
The cumulative distribution function (CDF) and the survival function of the EW distribution, denoted by 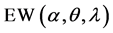 are respectively:
are respectively:
 , where
, where 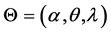 and
and 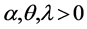 (1)
(1)
and
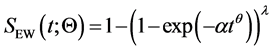 (2)
(2)
The 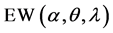 distribution generalizes the following distributions: 1) exponential distribution
distribution generalizes the following distributions: 1) exponential distribution 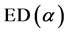 by setting
by setting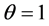 ,
,  , 2) Rayleigh distribution
, 2) Rayleigh distribution 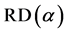 by setting
by setting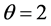 ,
,  , 3) generalized exponential distribution
, 3) generalized exponential distribution 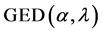 [21] by setting
[21] by setting 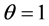 and 4) Weibull distribution
and 4) Weibull distribution  [22] [23] by setting
[22] [23] by setting .
.
Figure 1 represents the cumulative distribution function and the survival function of the 



The probability density function of the 

The corresponding hazard function has the form:

Figure 2 shows respectively the probability density function and the hazard rate function of the
Figure 1. Plots of cumulative distribution function and survival function of
Figure 2. Plots of probability density function and hazard rate function of the
distribution for different values of


2.1.1. Data Simulations of the 
By setting the three parameters








where

Figure 3 illustrate the empirical cdf, the cdf and the 95% lower and upper confidence bounds for the cdf of 100 simulated data by setting


2.1.2. Parameter Estimation
To estimate the parameters of the 





The log-likelihood function has the following form:

After calculating the first partial derivatives of 



To get the MLE of the parameters







Figure 3. Cdf and empirical cdf of the 
Table 1 gives the estimated parameters of 
2.2. Additive Weibull Distribution
The additive Weibull (AddW) distribution has four parameters




The cumulative distribution function of the 
Table 1. Parameter estimates of






The corresponding survival function is:

The 







Figure 4 shows respectively the cumulative distribution function and the survival function of the additive Weibull distribution for different values of



The probability density function of the 

The corresponding hazard function has the form:

Figure 5 shows the probability density function and the hazard rate function of the 




2.2.1. Data Simulations of the 
By setting the four parameters








where

Figure 6 illustrates the empirical cdf, the cdf and the 95% lower and upper confidence bounds for the cdf of the 100 simulated data by setting



2.2.2. Parameter Estimation
Now, we introduce the estimation of the model parameters by using the method of maximum likelihood. Let
Figure 4. Plots of cumulative distribution function and survival function of the
Figure 5. Plots of probability density function and hazard rate function of the
Figure 6. Cdf and empirical cdf of the







The log-likelihood function has the following form:

After calculating the first partial derivatives of 




To get out the MLE of the unknown parameters, we have to solve the above system of four non-linear equations with respect to



We obtain the second partial derivatives of 
Table 2 gives the estimated parameters of 10 simulations and the mean square error of each parameter.
3. Analysis of a Real Data Set
In this section, we analyze a real data set to demonstrate the performance of the EW and AddW distributions in practice. A sample of 50 components taken from Aarset [18] has been studied. For this data set, we compare at first the results of the fits of the EW distribution (EWD) against ED, GED, RD and WD which are sub-models of the EW distribution. In the second step the fits of the AddW distribution (AddWD) will be compared against WD, MWD, and LRFD which are sub-models of the AddW distribution. Table 3 gives the often used lifetimes of 50 devices introduced by Aarset. Table 4 and Table 5 show the MLE of the parameters, the log-likelihood function values and the MSD on the one hand for the ED, RD, GED, WD, EWD and on the other hand for the WD, MWD, LRFD, and the AddW models. Table 6 and Table 7 show the observed K-S test statistic values for each models EWD and AddWD and their correspondent sub-models and the p-value for each one. Figure 7 and Figure 8 show the plots of the empirical and fitted scaled TTT-Transforms, the empirical and parametric cumulative density functions, the empirical and fitted hazard and probability density functions for the models EWD, AddWD and their correspondent submodels.
However in Figure 9 we have a comparison between the two models EW and AddW. We note that for comparison purpose, we use the mean square difference between the empirical cdf and the fitted cdf, denoted by MSD. The MSD is computed by the following relation:

where 


Based on the results shown in Table 4 and Table 5, we could deduce that:
· compared with the MSD of the ED and the WD, the EWD is not the best fit of the Aarset data;
· the MSD of the AddWD has the lowest value compared with each sub-models, so the AddWD is the best in fitting the Aarset data;
· the MSD of the AddWD is smaller than the MSD of the EWD which indicates that the AddWD fits the given data better than the EWD.
Table 2. Parameter estimates of



Table 3. Lifetimes of 50 devices, Aarset.
Table 4. MLE of the parameter(s), log-likelihood function values and the MSD of sub-mod- els of the EWD.
Table 5. MLE of the parameter(s), log-likelihood function values and the MSD of sub-mod- els of the AddWD.
Table 6. The MLE of the parameter(s), K-S values and the associated p-values.
Table 7. The MLE of the parameter(s), K-S values and the associated p-values.
Figure 7. (a) The empirical and estimated scaled TTT-Transform plots of the ED, RD, GED, WD and EWD models; (b) The empirical and estimated cumulative density function of the ED, RD, GED, WD and EWD models; (c) Empirical and estimated hazard rate functions of the ED, RD, GED, WD and EWD models; (d) Empirical and estimated PDF of the ED, RD, GED, WD and EWD models, for Aarset data.
Figure 8. (a) The empirical and estimated scaled TTT-Transform plots of the WD, LRFD, MWD and AddWD models; (b) The empirical and estimated cumulative density function of the WD, LRFD, MWD and AddWD models; (c) Empirical and estimated hazard rate functions of the WD, LRFD, MWD and AddWD models; (d) Empirical and estimated pdf of the WD, LRFD, MWD and AddWD models, for Aarset data.
Figure 9. (a) The empirical and estimated scaled TTT-Transform plots of the EWD and AddWD models; (b) The empirical and estimated cumulative density function of the EWD and AddWD models; (c) Empirical and estimated hazard rate functions of the EWD and AddWD models; (d) Empirical and estimated PDF of the EWD and AddWD models, for Aarset data.
We perform in the next step at first the test of the following null hypotheses:
1) H0:

2) H0:

3) H0:
4) H0:
in favor of the alternative hypothesis Ha: the data follow the EWD “Exponentiated Weibull distribution”.
And on the other hand the test of the following null hypotheses.
1) H0:
2) H0:

3) H0:

in favor of the alternative hypothesis Ha: the data follow the AddWD “Additive Weibull distribution”.
In the following, we use a non parametric test statistics, Kolmogorov-Smirnov (K-S) test with a level of significance equal to 0.05, to test the null hypothesis mentioned below against Ha. We accept H0 with the p-value under the condition p-value > 0.05.
If we compare the EWD model with the sub-models ED, RD, GED and WD, we can conclude from Table 6 that:
· only the RD is rejected at level
· all H0’s excepted the RD are not rejected at
· the EWD is the best model among those discussed here, to fit the current data set because it has the biggest p-value (0.4732) and the lowest K-S value (0.1490).
Similarly, when we compare the AddWD model with the sub-models WD, LRFD and MWD, we can conclude from Table 7 that:
· none of H0’s is rejected at level
· the AddWD is the best model among those discussed here, to fit the current data set because it has the biggest p-value (0.7089) and the lowest K-S value (0.1230);
· the AddWD is the best model among the EWD model to fit the current data set because it has the lowest K-S value (0.1230).
We can immediately observe from Figure 7, Figure 8 and Figure 9 that: 1) the data set has a bathtub shaped hazard rate, 2) one can see the closeness of the fitted pdf using the AddWD model, 3) the AddWD fits the data set better than all other distributions used here, because its fitted curve is closer to the empirical curve.
4. Conclusion
In this paper, we show the performance of two models called the exponentiated Weibull distribution and the additive Weibull distribution by using an empirical comparison with the sub-models of each one such as the exponential distribution, the Rayleigh distribution, the generalized Weibull distribution, the linear failure rate distribution, the Weibull distribution and the modified Weibull distribution. The maximum likelihood estimations of the unknown parameters for these distributions are discussed. A real data set of Aarset is studied by using the EW and the AddW distributions. The results of the comparisons showed that the additive Weibull distribution provided a better fit for the Aarset data set than some of the often-used distributions.
References
- Weibull, W. (1951) A Statistical Distribution Function of Wide Applicability. Journal of Applied Mechanics, 18, 293-297.
- Murthy, D.N.P., Xie, M. and Jiang, R. (2003) Weibull Models. John Wiley & Sons, New York. http://dx.doi.org/10.1002/047147326X
- Bebbington, M., Lai, C.D. and Zitikis, R. (2007) A Flexible Weibull Extension. Reliability Engineering and System Safety, 92, 719-726. http://dx.doi.org/10.1016/j.ress.2006.03.004
- Zhang, T. and Xie, M. (2011) On the Upper Truncated Weibull Distribution and Its Reliability Implications. Reliability Engineering and System Safety, 96, 194-200. http://dx.doi.org/10.1016/j.ress.2010.09.004
- Mudholkar, G.S. and Srivastava, D.K. (1993) Exponentiated Weibull Family for Analyzing Bathtub Failure-Rate Data. IEEE Transactions on Reliability, 42, 299-302. http://dx.doi.org/10.1109/24.229504
- Sarhan, A.M. and Zaindin, M. (2009) Modified Weibull Distribution. Applied Sciences, 11, 123-136.
- Gasmi, S. and Berzig, M. (2011) Parameters Estimation of the Modified Weibull Distribution Based on Type I Censored Samples. Applied Mathematical Sciences, 59, 2899-2917.
- Marshall, A.W. and Olkin, I. (1997) A New Method of Adding a Parameter to a Family of Distributions with Application to the Exponential and Weibull Families. Biometrika, 84, 641-652. http://dx.doi.org/10.1093/biomet/84.3.641
- Xie, M., Tang, Y. and Goh, T.N. (2002) A Modified Weibull Extension with Bathtub-Shaped Failure Rate Function. Reliability Engineering and System Safety, 76, 279-285. http://dx.doi.org/10.1016/S0951-8320(02)00022-4
- Lai, C.D., Xie, M. and Murthy, D.N.P. (2003) Modified Weibull Model. IEEE Transactions on Reliability, 52, 33-37. http://dx.doi.org/10.1109/TR.2002.805788
- Xie, M. and Lai, C.D. (1996) Reliability Analysis Using an Additive Weibull Model with Bathtub Shaped Failure Rate Function. Reliability Engineering & System Safety, 52, 87-93. http://dx.doi.org/10.1016/0951-8320(95)00149-2
- Famoye, F., Lee, C. and Olumolade, O. (2005) The Beta-Weibull Distribution. Journal of Statistical Theory and Appli- cations, 4, 121-138.
- Cordeiro, G.M., Ortega, E.M. and Nadarajah, S. (2010) The Kumaraswamy Weibull Distribution with Application to Failure Data. Journal of the Franklin Institute, 347, 1399-1429. http://dx.doi.org/10.1016/j.jfranklin.2010.06.010
- Phani, K.K. (1987) A New Modified Weibull Distribution Function. Communications of the American Ceramic Society, 70, 182-184.
- Silva, G.O., Ortega, E.M. and Cordeiro, G.M. (2010) The Beta Modified Weibull Distribution. Lifetime Data Analysis, 16, 409-430. http://dx.doi.org/10.1007/s10985-010-9161-1
- Cordeiro, G.M., Nadarajah, S. and Ortega, E.M. (2013) General Results for the Beta Weibull Distribution. Journal of Statistical Computation and Simulation, 83, 1082-1114. http://dx.doi.org/10.1080/00949655.2011.649756
- Almalki, S.J. and Nadarajah, S. (2014) Modifications of the Weibull Distribution: A Review. Reliability Engineering and System Safety, 124, 32-55. http://dx.doi.org/10.1016/j.ress.2013.11.010
- Aarset, M.V. (1987) How to Identify Bathtub Hazard Rate. IEEE Transactions on Reliability, 36, 106-108. http://dx.doi.org/10.1109/TR.1987.5222310
- Mudholkar, G.S., Srivastava, D.K. and Freimer, M. (1995) The Exponentiated Weibull Family: A Reanalysis of the Bus-Motor-Failure Data. Technometrics, 37, 436-445. http://dx.doi.org/10.1080/00401706.1995.10484376
- Mudholkar, G.S. and Hutson, A.D. (1996) The Exponentiated Weibull Family: Some Properties and a Flood Data Application. Communications Statistical Theory Methods, 25, 3059-3083. http://dx.doi.org/10.1080/03610929608831886
- Gupta, R.D. and Kundu, D. (2007) Generalized Exponential Distribution: Existing Results and Some Recent Developments. Journal of Statistical Planning and Inference, 137, 3537-3547. http://dx.doi.org/10.1016/j.jspi.2007.03.030
- Gasmi, S., Love, C.E. and Kahle, W. (2003) A General Repair, Proportional-Hazards, Framework to Model Complex Repairable Systems. IEEE Transactions on Reliability, 52, 26-32. http://dx.doi.org/10.1109/TR.2002.807850
- Gasmi, S. (2011) Parameter Estimation in an Alternating Repair Model. Journal of Statistical Planning and Inference, 141, 3605-3616. http://dx.doi.org/10.1016/j.jspi.2011.05.013






























