Open Journal of Statistics
Vol.4 No.4(2014), Article
ID:47081,5
pages
DOI:10.4236/ojs.2014.44027
Probability Brainteasers for College Students
Sahand Rabbani1, Hossein Shahmohamad2
1Independent, Rochester, USA
2School of Mathematical Sciences, Rochester Institute of Technology, Rochester, USA
Email: hxssma@rit.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 April 2014; revised 26 April 2014; accepted 16 May 2014
ABSTRACT
We present eleven interesting problems in probability along with their solutions. These problems can be used as challenging and entertaining questions for high school or first-year college students.
Keywords:Probability, Statistics

1. Introduction
Quantitative brainteasers are more than just fascinating. They are parts of the natural pastime in engineering and science. The exact solution to a few may require greater computing power, but a satisfactory response without computer aid is provided in this paper. Two excellent references for material leading to these problems can be found in [1] or [2] .
1.1. Triangle
A stick of length L is randomly cut in two places. What is the probability that the three resulting pieces can form a triangle?
Solution: By depicting the event space as an l-by-l square in (x, y)-space, where the point (x, y) represents cuts at distances X and Y along the stick, it becomes evident that the probability is equal to the portion of the area bounded by certain linear constraints that ensure a triangle can be formed. This probability is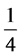 .
.
1.2. Disorganized Meet-Up
Two people have agreed to meet at a particular location between the hours of noon and 1 PM. Each individual will arrive uniformly and independently at a random time in this interval. If an individual arrives and the other is not there, the arriving party will wait for 20 minutes. If the other does not arrive within these 20 minutes, the waiting parting will leave. What is the probability that the two people will meet?
Solution: Plotting the event space on a 1 hr-by-1 hr grid and applying constraints that bound the area in which the two people meet reveals that the probability is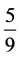 .
.
1.3. Collect Them All
Consider a brand of cereal that advertises a special prize in each of its cereal boxes. Suppose that there are n possible prizes and that any box of cereal contains each of these n prizes with equal probability, but which prize it contains is unknown until the box is opened. What is the expected number of cereal boxes that one must open to obtain all n prizes?
Solution: Define the random variable 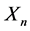 as the number of trials, or cereal box openings, until all n prizes are obtained. We seek
as the number of trials, or cereal box openings, until all n prizes are obtained. We seek . Consider the random variables
. Consider the random variables 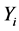 for
for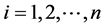 , where
, where 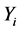 only has significance after n - i prizes have been obtained. The random variable
only has significance after n - i prizes have been obtained. The random variable 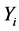 is the number of trials required to obtain one of the i remaining prizes. We can thus write
is the number of trials required to obtain one of the i remaining prizes. We can thus write 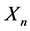 as
as
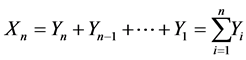
By the linearity of expectation, we have

We note that each 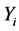 is a geometric random variable where the probability of success
is a geometric random variable where the probability of success ![]() is
is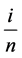 . The simplest case is
. The simplest case is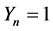 . When none of the prizes have been obtained, the expected number of trials to obtain one of the
. When none of the prizes have been obtained, the expected number of trials to obtain one of the  prizes is deterministic: open one cereal box and you have one of these n prizes. In general, the expected value of a geometric random variable with probability of success
prizes is deterministic: open one cereal box and you have one of these n prizes. In general, the expected value of a geometric random variable with probability of success ![]() is
is![]() . Thus, the expected value of
. Thus, the expected value of 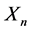 is
is
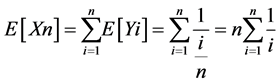
1.4. The Cuckoo Train
There are n passengers who have booked a seat on a full-capacity train ride. They are lined up to board the train, each passenger with a designated seat. Without loss of generality, we say that the nth passenger in line is assigned the nth seat. The first passenger to board, however, is an irrational man with no regard for Kants categorical imperative. Instead of sitting at his assigned seat, he randomly picks among the n seats. Each subsequent passenger to board, then, first looks to see if his assigned seat is available. If it is, he sits there. Otherwise, he picks randomly from the remaining seats. What is the probability that the last passenger will sit in his assigned seat?
Solution: Let us call the probability that the final passenger sits in his assigned seat![]() . Also, let us define the useful quantity
. Also, let us define the useful quantity![]() , which is the probability that the last person will sit in his assigned seat given an i-person subtrain with the initial person picking a random seat. Clearly,
, which is the probability that the last person will sit in his assigned seat given an i-person subtrain with the initial person picking a random seat. Clearly,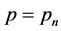 . Now, consider that when the first person boards, there is a probability
. Now, consider that when the first person boards, there is a probability 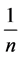 that he will pick his own seat, resulting in proper boarding with the final passenger sitting in his assigned seat as well. With probability
that he will pick his own seat, resulting in proper boarding with the final passenger sitting in his assigned seat as well. With probability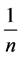 , he will pick the second person’s seat, after which the second passenger sees that his seat is taken and must then pick a random seat. In general, with the same probability
, he will pick the second person’s seat, after which the second passenger sees that his seat is taken and must then pick a random seat. In general, with the same probability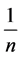 , the first passenger will pick the
, the first passenger will pick the ![]() th seat, after which boarding will proceed normally until the
th seat, after which boarding will proceed normally until the 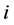 th passenger finds that his seat is taken, and he must pick a random seat:
th passenger finds that his seat is taken, and he must pick a random seat:
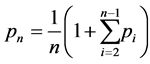
Thus,
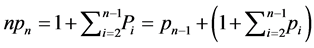
Also, 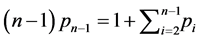 which implies
which implies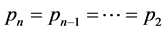 .
.
Clearly,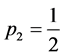 . This is the case where there are two seats and the first person randomly picks between his own seat and the seat of the last (second) passenger. Thus,
. This is the case where there are two seats and the first person randomly picks between his own seat and the seat of the last (second) passenger. Thus, . The final passenger will sit in his assigned seat with probability
. The final passenger will sit in his assigned seat with probability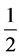 . Another solution considers that the only relevant event is whether a passenger sits in the first man’s seat, in which case the last man will get his seat, or sits in the last man’s seat, in which case the last man will not get his seat. If a passenger sits in any other seat, the same consideration is then deferred to the next boarding passenger. Since the probability of a man sitting in either the first man’s seat or the last man’s seat is equal, the probability of the last man getting his seat is equal to the probability of the last man not getting his seat, i.e.,
. Another solution considers that the only relevant event is whether a passenger sits in the first man’s seat, in which case the last man will get his seat, or sits in the last man’s seat, in which case the last man will not get his seat. If a passenger sits in any other seat, the same consideration is then deferred to the next boarding passenger. Since the probability of a man sitting in either the first man’s seat or the last man’s seat is equal, the probability of the last man getting his seat is equal to the probability of the last man not getting his seat, i.e.,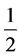 .
.
1.5. Heads, I Win
There is a two-headed coin and fifteen fair coins. One coin is chosen at random and flipped, coming up heads. What is the probability that this coin is the two-headed coin?
Solution: This is a simple application of Bayes rule: there are 17 head faces, two of which belong to the twoheaded coin. The conditional probability of a head face belonging to the two-headed coin is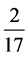 .
.
1.6. Tails, You Lose
1) There is a loaded coin that flips tails with probability![]() , where
, where ![]() is known only to be distributed uniformly on the interval [0,1]. The coin is flipped five times, each time turning up tails. What is the best estimate of
is known only to be distributed uniformly on the interval [0,1]. The coin is flipped five times, each time turning up tails. What is the best estimate of![]() ?
?
Solution: This is another application of Bayes rule:
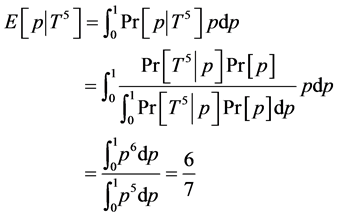
2) In general, what is the best estimate of p conditional on flipping the coin n times and observing exactly m tails?
Solution: The general solution is
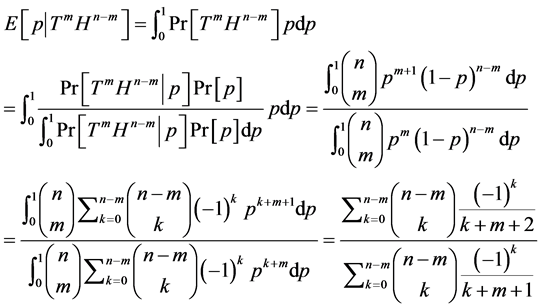
1.7. Metropolitan Transit Authority
There are ![]() sequentially numbered bus routes in a city. Knowing only that
sequentially numbered bus routes in a city. Knowing only that ![]() is uniformly distributed on
is uniformly distributed on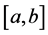 , one randomly observes a bus route numbered
, one randomly observes a bus route numbered . What is the best estimate of N based on this observation?
. What is the best estimate of N based on this observation?
Solution: Let  be the distribution of
be the distribution of ![]() conditional on
conditional on ![]() and let
and let 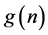 be the distribution of
be the distribution of![]() . Assume that
. Assume that ![]() and
and ![]() are continuous random variables for simplicity. The conditional expectation of
are continuous random variables for simplicity. The conditional expectation of ![]() given
given ![]() is
is
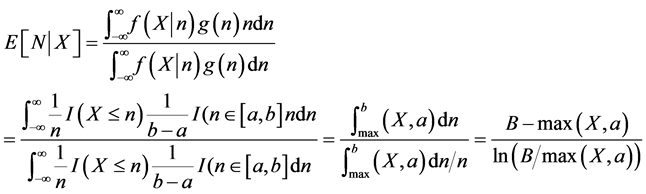
1.8. Bulls Eyes
There is an unusual dart board that has two equally sized non-overlapping circles of radius  whose centers are separated by some distance
whose centers are separated by some distance . In this dart game, if a dart lands inside of any of the circles, one point is scored; otherwise, no points are scored.
. In this dart game, if a dart lands inside of any of the circles, one point is scored; otherwise, no points are scored.
1) Where should you aim? Assume that the distribution around your aim is a zero-mean circular Gaussian with variance .
.
Solution: Roughly, for small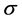 , you should aim at the center of one of the circles, and for large
, you should aim at the center of one of the circles, and for large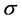 , you should aim between the two circles.
, you should aim between the two circles.
2) Having determined that the optimal aim point is a function of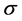 , is this function discontinuous such that there exists some
, is this function discontinuous such that there exists some  above which you should aim between the circles and below which you should aim at one of the centers?
above which you should aim between the circles and below which you should aim at one of the centers?
Solution: Based on numerical solutions for the one-dimensional case, the optimal aim is a continuous function of 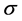 but may be non-differentiable at the point of smallest
but may be non-differentiable at the point of smallest  for which the optimal aim point is the center of one of the circles.
for which the optimal aim point is the center of one of the circles.
1.9. Synthetic Bet
There is a seven-game series sports event between Team A and Team B where the series winner is the first team to win four games. Single bets exist for each individual game with fair payout ![]() for Team A to win, but there is no bet available for the outcome of the entire series. Considering that bets for each individual game can be entered at any time prior to that game and can be placed in any amount, is there a betting strategy that pays fair-odds on the outcome of the entire series, and what is that strategy?
for Team A to win, but there is no bet available for the outcome of the entire series. Considering that bets for each individual game can be entered at any time prior to that game and can be placed in any amount, is there a betting strategy that pays fair-odds on the outcome of the entire series, and what is that strategy?
Solution: The possible paths and outcomes of this series can be depicted with a binomial tree. The desired payouts (or cash position) at the leaves of the tree are determined from the odds of Team A winning the entire series. The necessary cash position  and the quantity
and the quantity ![]() of the required bet at any intermediate node can be determined by the required cash position of the two possible succeeding nodes. Let a be the required cash position if Team A wins the game at the current node and b be the required cash position if Team B wins the game at the current node. These cash positions can be achieved exactly if the cash position at the current node is
of the required bet at any intermediate node can be determined by the required cash position of the two possible succeeding nodes. Let a be the required cash position if Team A wins the game at the current node and b be the required cash position if Team B wins the game at the current node. These cash positions can be achieved exactly if the cash position at the current node is
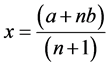 and a bet for Team A to win is placed in the amount of
and a bet for Team A to win is placed in the amount of . Using these formulas, the required cash position and required betting amount can be populated for every node in the binomial tree. Arguably the more challenging part of the problem is to determine the fair odds for Team A to win the entire series. In general, these odds are not n:1. The favored team wins the series with a higher probability than it wins an individual game. This problem is in some ways analogous to the discrete-time binomial pricing of derivatives contracts. At each stage, a replicating portfolio of cash and a risky instrument (a bet on the outcome of the next game) is maintained and subject to dynamic re-balance.
. Using these formulas, the required cash position and required betting amount can be populated for every node in the binomial tree. Arguably the more challenging part of the problem is to determine the fair odds for Team A to win the entire series. In general, these odds are not n:1. The favored team wins the series with a higher probability than it wins an individual game. This problem is in some ways analogous to the discrete-time binomial pricing of derivatives contracts. At each stage, a replicating portfolio of cash and a risky instrument (a bet on the outcome of the next game) is maintained and subject to dynamic re-balance.
1.10. A Good Deal
A standard deck of 52 cards contains 26 black cards and 26 red cards. You have the opportunity to play a game wherein you may flip over cards from the randomized deck one at a time. At any point, you may stop, and you receive $1 for every black card and pay $1 for every red card that has been turned over. What strategy achieves the maximum expected profit for this game and what is that profit?
Solution: Let 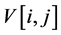 represent the expected profit from the optimal strategy in a game where the deck contains
represent the expected profit from the optimal strategy in a game where the deck contains ![]() black cards and
black cards and 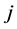 red cards. This function can be defined recursively. Under the optimal strategy, the expected profit of the
red cards. This function can be defined recursively. Under the optimal strategy, the expected profit of the 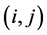 game is
game is
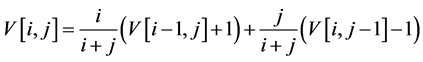
In the degenerate case where there are i black cards and no red cards, the value of the game is clearly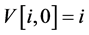 , since the optimal strategy is to turn over all the cards. In the converse where there are
, since the optimal strategy is to turn over all the cards. In the converse where there are 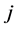 red cards and no black cards, the optimal strategy is not to turn over any cards:
red cards and no black cards, the optimal strategy is not to turn over any cards: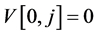 . Given the boundary conditions and the recursive formula, the entire grid of V can be easily populated to establish that the expected profit from the optimal strategy for a standard 52-card deck is approximately $2.6245. The optimal strategy is to flip over cards as long as
. Given the boundary conditions and the recursive formula, the entire grid of V can be easily populated to establish that the expected profit from the optimal strategy for a standard 52-card deck is approximately $2.6245. The optimal strategy is to flip over cards as long as 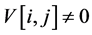 when in the
when in the 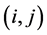 game.
game.
1.11. Adverse Selection
You have the opportunity to submit a single bid  on an object. You know that its intrinsic value
on an object. You know that its intrinsic value 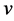 is uniformly distributed on
is uniformly distributed on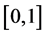 . If
. If , you win the object and pay
, you win the object and pay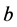 . If
. If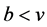 , you do not win the object and pay nothing. If you obtain the object, you can perform a costless modification that multiplies its value by
, you do not win the object and pay nothing. If you obtain the object, you can perform a costless modification that multiplies its value by  and then proceed to sell the object for
and then proceed to sell the object for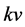 . What bidding strategy as a function of
. What bidding strategy as a function of  maximizes expected profits?
maximizes expected profits?
Solution: The conditional expected value of 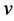 given that
given that  is a winning bid is
is a winning bid is . The conditional profit given that
. The conditional profit given that 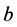 is a winning bid is then
is a winning bid is then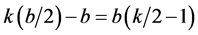 . The probability that
. The probability that 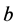 is a winning bid is b, so the expected profit of a bid b is
is a winning bid is b, so the expected profit of a bid b is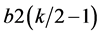 . For
. For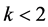 , this number is non-positive, so the optimal bid is 0. For
, this number is non-positive, so the optimal bid is 0. For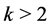 , this number is positive and maximized for the highest bid
, this number is positive and maximized for the highest bid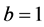 . For
. For , the expected profit is always 0, so any bid will do.
, the expected profit is always 0, so any bid will do.
References
- Evans, J.R. (2007) Statistics, Data Analysis, & Decision Modeling. Pearson/Prentice Hall, Upper Saddle River.
- Christensen, H.B. (1992) Introduction to Statistics. Saunders/HBJ, Orlando.

