Open Journal of Statistics
Vol.04 No.03(2014), Article ID:45274,12 pages
10.4236/ojs.2014.43020
Process Capability Indices for Shape Parameter of Weibull Distribution
Suboohi Safdar1, Ejaz Ahmed2
1Department of Statistics, University of Karachi, Karachi, Pakistan
2College of Computer Science and Information Systems, Institute of Business Management, Karachi, Pakistan
Email: suboohisafdar@yahoo.com, eahmed@iobm.edu.pk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 February 2014; revised 10 March 2014; accepted 17 March 2014
ABSTRACT
Process capability analysis is used to determine the process performance as capable or incapable within a specified tolerance. Basic indices Cp, Cpk, Cpm, Cpmk initially developed for normally distributed processes showed inappropriate for processes with non-normal distributions. A number of authors worked on non-normal distributions which were most notably those of Clements, Pearn and Chen, Montgomery and Johnson-Kotz-Pearn (JKP). Obtaining PCIs based on the parameters of non-normal distributions are completely disregarded and ignored. However parameters of some non-normal distributions have significance for knowing the status of process as capable or incapable. In this article we intend to work on the shape parameter of Weibull distribution to calculate PCIs. We work on two data sets for verification and validation purpose. Efficacy of the technique is assessed by bootstrapping the results of estimate and standard error of shape parameter.
Keywords:
Regression Coefficient; Non-Normal Distribution; Delta Method; Bootstrapping

1. Introduction
Process capability indices (PCIs) reflect the potential of a process performance by a unit-less measure. These indices have been used to check a statistical controlled process capability of producing items that meets the quality condition predetermined by the product designer, basic indices as Cp by Juran [1] , Cpk by Kane [2] , Cpm by Chan et al. [3] , and Cpmk by Pearn et al. [4] . For detailed description see Johnson and Kotz [5] . Vannman [6] constructed a superstructure for the generalization of these basic indices. These basic indices developed and designed for normal processes give flawed results for non-normal processes. Gunter [7] presented a series of four papers based on non-normal indices; Boyles [8] worked for asymmetric tolerance; and Zwick [9] proposed a hybrid method for fitting of distribution and many more methods are designed and modified for estimating PCIs for non-normal distributions. Most of the indices designed for non-normal processes are based on transformation or percentile method. Johnson [10] proposed Johnson transformation system based on moment method. Box and Cox [11] presented a family of power transformations for analysis of non-normal data. Clements’ [12] using Pearson family of curves proposed a percentile-based method. English and Taylor [13] discussed expected loss for process measurement arising from normal and non-normal distributions. Pearn and Kotz [14] worked on Clements method for calculating second and third generation process capability indices for non-normal Pearsonian populations. Schneider and Pruett [15] used the capability indices for the supplier certification process. Castagliola [16] approach is based on calculating the probability of non-conforming data using Burr distribution for non-normal population. Montgomery [17] discussed the indices for non-normal population. Kotz and Lovelace [18] constructed tables of standardized tails of Pearson curves. Tong and Chen [19] discussed the lower confidence limit for non-normal distributions. Choi and Bai [20] developed a weighted variance (WV) method for skewed population. Liu and Chen [21] suggested that the accuracy of estimated PCI for non-normal data can be improved by using Burr distribution instead of Pearson curve percentiles. Chang, Chen and Hsieh [22] developed an index that could be used for non-normal populations efficiently and many more. We may note that work on parameters of non-normal distribution is always ignored by quality practitioners. The purpose of this article is to report the results of PCIs based on Weibull shape parameter using the regression method of two data sets and consider its shape parameter as a quality characteristic of a statistical controlled process. The proposed procedure reflects accurately the significance of Weibull shape parameter.
This article is organized as follows. In Section 2, we describe few special features of Weibull distribution; propose procedure to obtain process parameters of Weibull shape parameter to estimate PCIs from earlier proposed superstructure forms. In Section 3, we analyze the two data sets and observe the effect of shape parameter on PCIs. In Section 4, we conclude the proposed procedure and in Section 5, we discuss some applications of Weibull distribution.
2. Research Methodology
2.1. Weibull Distribution EV-III
The Weibull distribution is first applied by Swedish Physicist W. Weibull in the 1930s in studying material strength in tension and fatigue. This distribution is extensively used in reliability and lifetime modeling fatigue and survival analysis and to model an extensive range of failure rates because of its flexible shape.
The two parameter Weibull distribution has density function as;
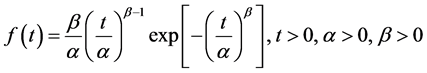 (1)
(1)
where 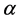 is the scale and
is the scale and 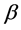 is the shape parameter of Weibull distribution
is the shape parameter of Weibull distribution
The cumulative distribution function of Weibull distribution is as
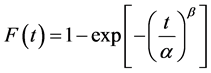 (2)
(2)
Equation (2) becomes the cumulative distribution function of exponential distribution for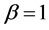 . Confidence limits on the value of
. Confidence limits on the value of  for sample of size n can be determined as
for sample of size n can be determined as
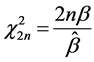 (3)
(3)
If  is greater than 1, the distribution is significantly different from the exponential.
is greater than 1, the distribution is significantly different from the exponential.
The different 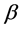 values are sensitive to the shape of the distribution and increasing
values are sensitive to the shape of the distribution and increasing  reduces the skewness of Weibull distribution. For
reduces the skewness of Weibull distribution. For 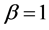 the distribution reduce to exponential, for
the distribution reduce to exponential, for 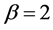 the distribution is Rayleigh and resemble to normal for
the distribution is Rayleigh and resemble to normal for . For higher values of
. For higher values of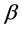 , the curves tends to become symmetrical. Variety of scale parameter
, the curves tends to become symmetrical. Variety of scale parameter  has no effect, for the fact the scale parameter
has no effect, for the fact the scale parameter 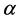 set to 1, in simulation studies.
set to 1, in simulation studies.
Figure 1 shows the behavior of various values of shape parameter 

Aleksander and Thierry [23] developed the stress gradient effect on fatigue life of structural components. In their approach the shape coefficient of the Weibull distribution becomes a function of a local damage parameter. The function also observed relationship between the shape of the fatigue life distribution and the stress level. Zhang, Xie and Tang [24] used Weibull shape parameter as a measure of reliability and compared various estimators based on different assumptions. The Weibull shape parameter has significance to determine the behavior of the failure rate of the product or system in measuring time to failure in any electrical or mechanical system. The log-normal shape parameter affects the skewness and kurtosis-increase (decrease) in this parameter results in larger (smaller) skewness and kurtosis values.
We may thus conclude that the variation in shape parameter is sensitive for measuring the process capability.
2.2. Sampling Distribution of Shape Parameter of Weibull Distribution
There are many methods proposed for estimation of parameters of known theoretical distribution as maximum likelihood estimation method, method of moments, regression methods etc. For our capability index based on Weibull shape parameter we prefer regression method. This method is easy and straight forward even for obtaining the standard errors of the parameters without involving iterative procedures as required for other methods of estimation see Ahmed and Safdar [25] . Once the sampling distribution (estimate and standard error) of parameter is recognized the behavior (normal or non-normal) of the parameter is easy to determine.
The simple linear regression model with only one independent variable (regressor) is

This model has two regression parameters 







Figure 1. Weibull probability density function.

Suppose that 




Taking 


For plotting position

mator) is used for an efficient approximation of complete samples. Here i is the rank of the data in ascending order, n is number of items in data and 
Comparing Equation (8) with Equation (4) we have 





One may note the estimator of 
Now we have


The estimate and standard error for Weibull shape parameter using the above method are estimated using the nls function based on delta method in R-console version 3.0.1 [28] .
2.3. PCIs for Shape Parameter of Weibull Distribution
The sampling distribution of regression coefficients of a linear regression model follows t-distribution. The histogram and the box plot for the estimated parameter for different size (or bootstrap) showed the symmetrical behavior (see Figure 2 and Figure 3). In this present paper data sets has specification limits for the non-normal





Figure 2. Histogram and box plot of beta for boot parameters B = 20, 30, 40, 50, 100 of annual minimum daily flow.
processes but for parameters (shape and scale) we do not have any set specification limits. Based on the sampling distribution of regression parameters we may estimate the limits by
We check the normality by histogram with density curve and box plot. We drew sample of size 50 to obtain the sampling distribution of shape parameter 


We have used the following superstructures earlier proposed by numerous authors for normal and non-normal populations to estimate PCIs for Weibull shape parameter
(Normal) Vannman [5] superstructure assuming Normal 
Clements [12] and Pearn and Chan [29] 





Figure 3. Histogram and box plot of beta fir boot parameters B = 20, 30, 40, 50 and 100 of Pearn and Chan measurements.
(PC) Pearn and Chan [29] where estimates are based on sample percentiles, Chang and Lu [30]

(PKJ) Pearn and Kotz [14] , and Pearn and Chen [31] applied Clements method [12] to estimate indices

Table 1. PCIs of Weibull shape parameter for annual minimum daily flow.
Table 2. PCIs of Weibull shape parameter for Pearn and Chan measurement.
3. Data Sets from Weibull Distribution
To illustrate how to calculate the PCIs based on shape parameter of Weibull distribution, we used two data sets and obtain the results of indices given in Equations (11a)-(11d).
3.1. Annual Minimum Daily Flow
The data consisting of 22 annual minimum mean daily flows, given in m3/s, were recorded at the proposed diversion site in the Hasdo subcatchment of the Mahanadi basin in India pp-236 [26] .
Assuming annual minimum flow follows two parameter Weibull distributions with shape parameter 2.29 and scale parameter 2.67. These parameters are estimated from the mean and variance of the given data sets.
Table 1 comprises the results of PCIs of Weibull shape parameter based on four different superstructures with various sample sizes.
The reason for estimating PCIs for annual minimum daily flow is the notice on the variation when we vary the magnitude of shape parameter in either direction. It is observed that the probability that an annual minimum low flow will be less than 2 m3/s over a two-year period is 0.40. This probability decreases by increasing the magnitude of the shape parameter from 2.29 and increases by decreasing the magnitude. So the stability of annual minimum low flow may analyzed by obtaining PCIs based on the shape parameter of the Weibull distribution.
Figure 2 shows the graphical variation with sample size for each bootstrap sample of annual minimum low flow data.
We may observe from the analysis a single conclusion that Weibull shape parameter may use in the place of measurements coming from Weibull distribution. So in any industrial or mechanical production of process follows Weibull distribution with known parameters, capability indices using the proposed procedures can be obtained in a very straightforward way along with statistical process control tools.
3.2. Pearn and Chan Used Rubber Edge Measurements [29]
Pearn and Chan used rubber edge measurements to exemplify his proposed generalization of basic indices to cover non-normal distributions. Rubber edge of a speaker woofer driver is one of the key components which reflect the sound quality of the driver units, such as musical image and clarity of the sound. One characteristic of the rubber edge is weight which is considered here as a quality characteristic. Since the sound quality is time dependent for any life-time system so use of this data as Weibull distribution is justified. We used a sample of size 80 from Pearn and Chen measurements [29] .
The shape and scale parameter based on mean and standard deviation are found 259.1926 and 8.681957. The probability that process produce the weight of rubber edge on target (T = 8.7) at these parameters is found to be 0.819, if beta is increased by 10 the probability becomes 0.826 and 0.813 by decreasing the beta to 10. These variations in probabilities justified the use of PCIs for the shape parameter of the Weibull distribution.
Table 2 comprises the results of PCIs of Weibull shape parameter on four superstructures with sample sizes.
Figure 3 shows graphical variation of sample size for each bootstrap sample of Pearn and Chan measurements.
For the data set of Pearn and edge measurements if shape parameter which should be the function of weight selected by process designer increases the chance that process producer the rubber edge of speaker woofer driver on target might be increases for this case.
4. Concluding Remarks
In this research paper we are the first who discussed the PCIs based on shape parameter of Weibull distribution that have been disregarded always. The importance of shape parameter cannot be ignored in making a process behavior symmetrical or skewed. Some other non-normal distributions as Gumbel (EVI) or fatigue reliability distribution can also be assessed using this technique. In studying of estimating the PCIs for the shape parameter of Weibull distribution for the data sets (discussed in Section 3.1 and 3.2), we noted that the process stability depended on the parameters of the distribution. One can show that the annual minimum low flow as stable or instable and the quality of woofer speaker as good or bad might be the functions of the magnitude of the shape parameter. We also observed that the size of the sample has no one-to-one influence on capability of a process. We used the three popular generalizations by Clements [12] , Pearn and Kotz [14] and Pearn and Chen [29] proposed for non-normal distribution to estimate the PCIs. Our task is to estimate the PCIs of the shape parameter of the non-normal distribution, but not to propose modifying the developed procedures for estimating PCIs.
In studying of estimating the PCIs for the shape parameter of Weibull distribution for two data sets, we noted that the process stability also depended on shape parameters of the distribution. We also observed that the size of the sample has no significant effect on capability of a process.
5. Application for Weibull Distribution
This distribution provides the close approximation to the probability laws of many natural phenomena as estimation of low flows, time to failure for an electrical and mechanical system(s), earthquakes or floods breaking strengths in censored or truncated situations and many more. Few examples are Lieblein and Zelen [32] investigated fatigue life of ball bearing. Kao [33] characterized lifetime of electron tubes. Milkolaj [34] suggested environmental application on Beach tar deposition process. Piotrovskii [35] used Weibull distribution for drug molecules in vivo absorption times. Padgett and Spurrier [36] used Shewhart type control charts for strength distributions. Bracho [37] discussed the application of Weibull Model to describe the vacuum pulse osmotic dehydration of sardine sheets. Basu et al. [38] discussed the strength distribution of certain structural ceramic and glass material using Weibull distribution. Guo and Wang [39] constructed the control charts for monitoring the Weibull shape parameter based on Type II censored sample.
Acknowledgements
The authors thank the Editor-in-Chief Prof. Qihua Wang (Chinese Academy of Sciences, China) and the anonymous referees for their careful reading of the paper and their suggestions which improved the paper.
References
- Juran, J.M. (1974) Juran’s Quality Control Handbook. 3rd Edition. McGraw-Hill, New York.
- Kane, V.E. (1986) Process Capability Indices. Journal of Quality Technology, 18, 41-52.
- Chan, L.K., Cheng, S.W. and Spiring, F.A. (1988) A New Measure of Process Capability: Cpm. Journal of Quality Technology, 20, 162-175.
- Pearn, W.L., Kotz, S. and Johnson, N.L. (1992) Distributional and Inferential Properties of Process Capability Indices. Journal of Quality Technology, 24, 216 -231.
- Kotz, S. and Johnson, N.L. (1993) Process Capability Indices. Chapman & Hall, Suffolk.
- Vannman, K. (1995) A Unified Approach to Capability Indices. Statistica Sinica, 5, 805-820.
- Gunter, B.H. (1989) The Use and Abuse of Cpk. Quality Progress, 22, 108-109.
- Boyles, R.A. (1994) Process Capability with Asymmetric Tolerance. Communications in Statistics: Simulations and Computation, 23, 615-643. http://dx.doi.org/10.1080/03610919408813190
- Zwick, D. (1995) A Hybrid Method for Fitting Distributions to Data and It Use in Computing Process Capability Indices. Quality Engineering, 7, 601-613. http://dx.doi.org/10.1080/08982119508918806
- Johnson, N.L. (1949) System of Frequency Curves Generated by Translation. Biometrika, 36, 149-176.
- Box, G.E.P. and Cox, D.R. (1964) An Analysis of Transformation. Journal of Royal Statistical Society, 26, 211-243.
- Clements, J.A. (1989) Process Capability Calculations for Non-Normal Distributions. Quality Progress, 22, 95-100.
- English, J.R. and Taylor, G.D. (1993) Process Capability Analysis—A Robustness Study. International Journal of Production Research, 31, 1621-1635. http://dx.doi.org/10.1080/00207549308956813
- Pearn, W.L. and Kotz, S. (1994) Application of Clements’ Method for Calculating Second and Third Generation Process Capability Indices for Non-Normal Pearsonian Populations. Quality Engineering, 7, 139-145. http://dx.doi.org/10.1080/08982119408918772
- Schneider, H. and Pruett, J. (1995) Uses of Process Capability Indices in the Supplier Certification Process. Quality Engineering, 9, 225-235. http://dx.doi.org/10.1080/08982119508904621
- Castagliola, P. (1996) Evaluation of Non-Normal Process Capability Indices Using Burr’s Distributions. Quality Engineering, 8, 587-593. http://dx.doi.org/10.1080/08982119608904669
- Somerville, S.E. and Montgomery, D.C. (1996-1997) Process Capability Indices and Non-Normal Distributions. Quality Engineering, 19, 305-316. http://dx.doi.org/10.1080/08982119608919047
- Kotz, S. and Lovelace, C.R. (1998) Process Capability Indices in Theory and Practice. Arnold, London.
- Tong, L.I. and Chen, J.P. (1998) Lower Confidence Limits of Process Capability Indices for Non-Normal Process Distribution. International Journal of Quality and Reliability Management, 15, 907-919. http://dx.doi.org/10.1108/02656719810199006
- Bai, D.S., Chang, Y.S. and Choi, S.I. (2002) Process Capability Indices for Skewed Populations. Quality and Reliability Engineering International, 18, 383-393. http://dx.doi.org/10.1002/qre.489
- Liu, P.H. and Chen, F.L. (2006) Process Capability Analysis of Non-Normal Process Data Using the Burr XII Distribution. International Journal of Advanced Manufacturing Technology, 27, 975-984. http://dx.doi.org/10.1007/s00170-004-2263-8
- Chang, L., Chen, S.C. and Hsieh, C.Y. (2007) Capability Indices for Non-Normal Populations. Journal of Statistics and Management Systems, 10, 183-193. http://dx.doi.org/10.1080/09720510.2007.10701247
- Aleksander, K. and Thierry, P.L. (2013) Modeling of Stress Gradient Effect of Fatigue Life Using Weibull Based Distribution Function. Journal of Theoretical and Applied Mechanics, 51, 297-311.
- Yavuz, A.A. (2013) Estimation of the Shape Parameter of the Weibull Distribution Using Linear Regression Methods: Non-Censored Samples. Quality and Reliability Engineering, 29, 1207-1219. http://dx.doi.org/10.1002/qre.1472
- Ahmed, E. and Safdar, S. (2010) Process Capability Analysis for Non-Normal Data. Pakistan Business Review, 234- 243.
- Kottegoda, N.T. and Renzo, R. (1997) Statistics, Probability and Reliability for Civil and Environmental Engineers. McGraw Hill International Editions, New York, 216-217.
- Kendall, M.G. and Stuart, A. (1977) The Advanced Theory of Statistics. Macmillan, New York, Vol. 1, 168.
- R Core Team (2013) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna. http://www.R-project.org/
- Pearn, W.L. and Chen, K.S. (1997) Capability Indices for Non-Normal Distributions with an Application in Electrolytic Capacitor Manufacturing. Microelectronics Reliability, 37, 1853-1858. http://dx.doi.org/10.1016/S0026-2714(97)00023-1
- Chang, P.L. and Lu, K.H. (1994) PCI Calculations for Any Shape of Distribution with Percentile. Quality World, Tech- nical Section, 20, 110-114.
- Pearn, W.L. and Chen, K.S. (1995) Estimating Process Capability Indices for Non-Normal Pearsonian Populations. Quality and Reliability Engineering International, 11, 386-388. http://dx.doi.org/10.1002/qre.1472
- Lieblein, J. and Zelen, M. (1956) Statistical Investigation of the Fatigue Life of Deep-Groove Ball Bearings. Journal of Research of the National Bureau of Standards, 57, 273-315. http://dx.doi.org/10.6028/jres.057.033
- Kao, J. (1959) A Graphical Estimation of Mixed Weibull Parameters in Life-Testing of Electron Tubes. Technometrics, 1, 389-407. http://dx.doi.org/10.1080/00401706.1959.10489870
- Milkolaj, G. (1972) Environmental Applications of the Weibull Distribution Function. Oil Pollution Science, 176, 1019-1021.
- Piotrovskii, V.K. (1987) The Use of Weibull Distribution to Describe the in Vivo Absorption Kinetics. Journal of Pharmacokinetics and Pharmacodynamics, 15, 681-686. http://dx.doi.org/10.1007/BF01068420
- Padgett, W.J. and Spurrier, J.D. (1990) Shewhart-Type Charts of Percentiles of Strength Distributions. Journal of Qua- lity Technology, 22, 283-288.
- Corzo, O. and Bracho, N. (2008) Application of Weibull Distribution Model to Describe the Vacuum Pulse Osmotic Dehydration of Sardine Sheets. LWT-Food Science and Technology, 41, 1108-1115.
- Basu, B., Tiwari, D., Kundu, D. and Prasad, R. (2009) Is Weibull Distribution the Most Appropriate Statistical Stren- gth Distribution for Brittle Materials? Ceramics International, 35, 237-246. http://dx.doi.org/10.1016/j.ceramint.2007.10.003
- Guo, B.C. and Wang, B.X. (2012) Control Charts for Monitoring the Weibull Shape Parameter Based on Type-II Censored Sample. Quality and Reliability Engineering International, 30, 13-24. http://dx.doi.org/10.1002/qre.1473





