Open Journal of Statistics
Vol.4 No.2(2014), Article ID:43295,18 pages DOI:10.4236/ojs.2014.42015
Nonlinear Principal and Canonical Directions fromContinuous Extensions of Multidimensional Scaling
Carles M. Cuadras
Department of Statistics, University of Barcelona, Barcelona, Spain
Email: ccuadras@ub.edu
Copyright © 2014 Carles M. Cuadras. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Carles M. Cuadras. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 26, 2013; revised January 26, 2014; accepted February 4, 2014
ABSTRACT
A continuous random variable is expanded as a sum of a sequence of uncorrelated random variables. These variables are principal dimensions in continuous scaling on a distance function, as an extension of classic scaling on a distance matrix. For a particular distance, these dimensions are principal components. Then some properties are studied and an inequality is obtained. Diagonal expansions are considered from the same continuous scaling point of view, by means of the chi-square distance. The geometric dimension of a bivariate distribution is defined and illustrated with copulas. It is shown that the dimension can have the power of continuum.
Keywords: Statistical Distances; Orthogonal Expansions; Principal Directions of Random Variables; Diagonal Expansions; Copulas; Uncountable Dimensionality
1. Introduction
Let ![]() be a random variable on a probability space
be a random variable on a probability space  with range
with range , absolutely continuous cdf
, absolutely continuous cdf 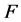 and density
and density 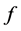 w.r.t. the Lebesgue measure. Our main purpose is to expand (a function of)
w.r.t. the Lebesgue measure. Our main purpose is to expand (a function of) ![]() as
as
 (1)
(1)
where 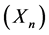 is a sequence of uncorrelated random variables, which can be seen as a decomposition of the so-called geometric variability
is a sequence of uncorrelated random variables, which can be seen as a decomposition of the so-called geometric variability 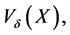 defined below, a dispersion measure of
defined below, a dispersion measure of ![]() in relation with a suitable distance function
in relation with a suitable distance function  Here orthogonality is synonymous with a lack of correlation.
Here orthogonality is synonymous with a lack of correlation.
Some goodness-of-fit statistics, which can be expressed as integrals of the empirical processes of a sample, have expansions of this kind [1-3]. Expansion (1) is obtained following a similar procedure, except that we have a sequence of uncorrelated rather than independent random variables. Finite orthogonal expansions appear in analysis of variance and in factor analysis. Orthogonal expansions and series also appear in the theory of stochastic processes, in martingales in the wide sense ([4], Chap. 4; [5], Chap. 10), in non-parametric statistics [6], in goodness-of-fit tests [7,8], in testing independence [9] and in characterizing distributions [10].
The existence of an orthogonal expansion and some classical expansions is presented in Section 2. A continuous extension of matrix formulations in multidimensional scaling (MDS), which provides a wide class of expansions, is presented in Section 3. Some interesting expansions are obtained in Section 4 for a particular distance as well as additional results, such as an optimal property of the first dimension. Section 5 contains an inequality concerning the variance of a function. Section 6 is devoted to diagonal expansions from the continuous scaling point of view. Sections 7 and 8 are devoted to canonical correlation analysis, including a continuous generalization. This paper extends the previous results on continuous scaling [11-14], and other related topics [15,16].
2. Existence and Classical Expansions
There are many ways of obtaining expansion (1). Our aim is to obtain some explicit expansions with good properties from a multivariate analysis point of view. However, before doing this, let us prove that a such expansion exists and present some classical expansions.
Theorem 1. Let ![]() be an absolutely continuous r.v. with density
be an absolutely continuous r.v. with density  and support
and support 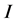 and
and 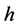 a measurable function such that
a measurable function such that 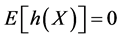 and
and 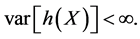 Then there exists a sequence
Then there exists a sequence 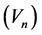 of uncorrelated r.v.’s such that
of uncorrelated r.v.’s such that
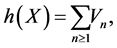 (2)
(2)
with  where the series
where the series 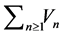 converges in the mean square as well as almost surely.
converges in the mean square as well as almost surely.
Proof. Consider the Lebesgue spaces  and
and  of measurable functions
of measurable functions 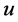 on
on 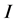 such that
such that 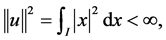 and
and 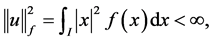 respectively. Obviously,
respectively. Obviously,  and
and 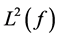 are separable Hilbert spaces with quadratic-norms
are separable Hilbert spaces with quadratic-norms ![]() and
and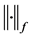 , respectively. Moreover
, respectively. Moreover  given by
given by 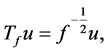
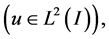 is a linear isometry of
is a linear isometry of 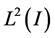 onto
onto 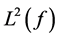 i.e.,
i.e., 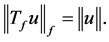
Let 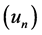 be an orthonormal basis for
be an orthonormal basis for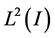 . Accordingly,
. Accordingly,  given by
given by
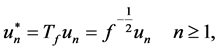
is an orthonormal basis for . The assumption
. The assumption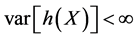 , together with
, together with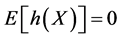 , is equivalent to
, is equivalent to . In fact,
. In fact, 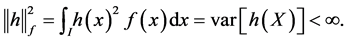 Hence
Hence 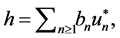 where
where 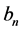 are the Fourier coefficients and
are the Fourier coefficients and  Letting
Letting 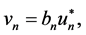 we deduce that
we deduce that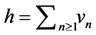 , where the series converges in
, where the series converges in 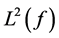 and
and 
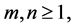 where
where 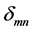 is Kronecker’s delta. Replacing
is Kronecker’s delta. Replacing 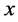 by
by![]() , and defining
, and defining , we obtain
, we obtain 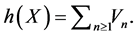
This series converges almost surely, since the series 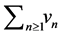 converges in
converges in 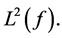 We may suppose
We may suppose 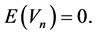 Next, for
Next, for , we have cov
, we have cov 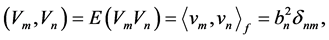 as asserted. Finally, note that
as asserted. Finally, note that 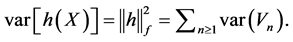 In particular, the series in (2) converges also in the mean square. W Some classical expansions for
In particular, the series in (2) converges also in the mean square. W Some classical expansions for ![]() or a function of
or a function of ![]() are next given.
are next given.
2.1. Legendre Expansions
Let 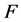 be the cdf of
be the cdf of ![]() An all-purpose expansion can be obtained from the shifted Legendre polynomials
An all-purpose expansion can be obtained from the shifted Legendre polynomials 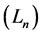 on
on 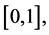 where
where 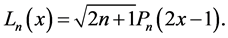 The first three are
The first three are

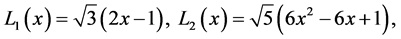
Note that 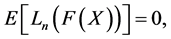
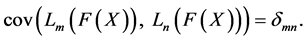 Thus we may consider the orthogonal expansion
Thus we may consider the orthogonal expansion
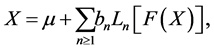
where  and
and 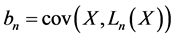 are the Fourier coefficients. This expansion is quite useful due to the simplicity of these polynomials, is optimal for the logistic distribution, but may be improved for other distributions, as it is shown below.
are the Fourier coefficients. This expansion is quite useful due to the simplicity of these polynomials, is optimal for the logistic distribution, but may be improved for other distributions, as it is shown below.
2.2. Univariate Expansions
A class of orthogonal expansions arises from
 (3)
(3)
where both 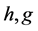 are probability density functions. Then
are probability density functions. Then 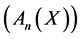 is a complete orthonormal set w.r.t.
is a complete orthonormal set w.r.t. ![]()
2.3. Diagonal Expansions
Lancaster [17] studied the orthogonal expansions
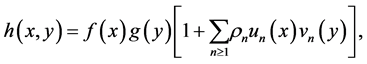 (4)
(4)
where  is a bivariate probability density with marginal densities
is a bivariate probability density with marginal densities 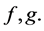 Then
Then 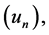
 are complete orthonormal sets w.r.t
are complete orthonormal sets w.r.t 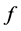 and
and ![]() respectively. Moreover
respectively. Moreover 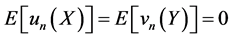 and
and 
 where
where 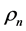 is the n-th canonical correlation between
is the n-th canonical correlation between ![]() and
and ![]()
Expansion (4) can be viewed as a particular extension of Theorem 3, proved below, when the distance is the so-called chi-square distance. This is proved in [18]. See Section 6.
3. Continuous Scaling Expansions
In this section we propose a distance-based approach for obtaining orthogonal expansions for a r.v.![]() , which contains the Karhunen-Loève expansion of a Bernoulli process related to
, which contains the Karhunen-Loève expansion of a Bernoulli process related to ![]() as a particular case. We will prove that we can obtain suitable expansions using continuous multidimensional scaling on a Euclidean distance.
as a particular case. We will prove that we can obtain suitable expansions using continuous multidimensional scaling on a Euclidean distance.
Let 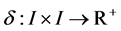 be a dissimilarity function, i.e.,
be a dissimilarity function, i.e., 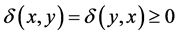 and
and 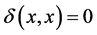 for all
for all 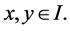
Definition 1. We say that ![]() is a Euclidean distance function if there exists an embedding
is a Euclidean distance function if there exists an embedding 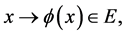
where 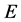 is a real separable Hilbert space with quadratic norm
is a real separable Hilbert space with quadratic norm![]() , such that
, such that 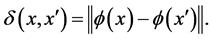
We may always view the Hilbert space 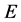 as a closed linear subspace of
as a closed linear subspace of  In this case, we may identify
In this case, we may identify  with
with 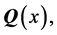 where for
where for 
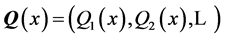 is a vector in
is a vector in  Accordingly, for
Accordingly, for 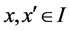
 (5)
(5)
Definition 2.  is called a Euclidean configuration to represent
is called a Euclidean configuration to represent 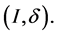 The geometric variability of
The geometric variability of ![]() w.r.t.
w.r.t. ![]() is defined by
is defined by
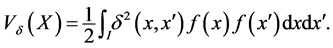
The proximity function of 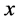 to
to ![]() is defined by
is defined by
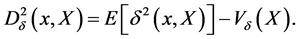 (6)
(6)
The double-centered inner product related to ![]() is the symmetric function
is the symmetric function
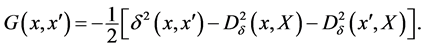 (7)
(7)
These definitions can easily be extended to random vectors. For example, if  is
is 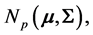
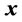 is an observation of
is an observation of 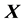 and
and ![]() is the Euclidean distance in
is the Euclidean distance in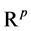 , then
, then 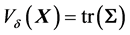 and
and 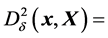
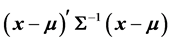 is the Mahalanobis distance from
is the Mahalanobis distance from  to
to ![]()
The function ![]() is symmetric, semi-definite positive and satisfies
is symmetric, semi-definite positive and satisfies
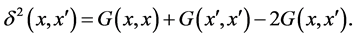 (8)
(8)
It can be proved [19], that there is an embedding 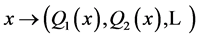 of
of 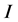 into
into ![]() such that
such that
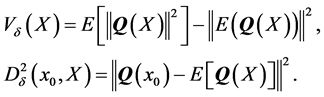
G is the continuous counterpart of the centered inner product matrix computed from a  distance matrix and used in metric multidimensional scaling [20,21]. The Euclidean embedding or method of finding the Euclidean coordinates from the Euclidean distances was first given by Schoenberg [22]. The concepts of geometric variability and proximity function, were originated in [23] and are used in discriminant analysis [19], and in constructing probability densities from distances [24]. In fact,
distance matrix and used in metric multidimensional scaling [20,21]. The Euclidean embedding or method of finding the Euclidean coordinates from the Euclidean distances was first given by Schoenberg [22]. The concepts of geometric variability and proximity function, were originated in [23] and are used in discriminant analysis [19], and in constructing probability densities from distances [24]. In fact, 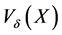 is a variant of Rao’s quadratic entropy [25]. See also [14,26].
is a variant of Rao’s quadratic entropy [25]. See also [14,26].
In order to obtain expansions, our interest is on 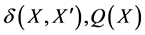 and
and 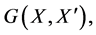 i.e., we substitute
i.e., we substitute  by the r.v.
by the r.v. ![]()
For convenience and analogy with the finite classic scaling, let us use a generalized product matrix notation (i.e., a “multivariate analysis notation”), following [18]. We write 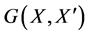 as
as  where
where 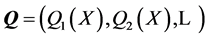 is a Euclidean centered configuration to represent
is a Euclidean centered configuration to represent  according to (5), (8), i.e., we substitute
according to (5), (8), i.e., we substitute 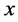 by
by ![]() in
in 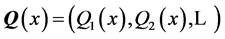 and suppose that each
and suppose that each 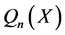 has mean 0. The covariance matrix of
has mean 0. The covariance matrix of 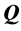 is
is 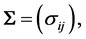 where for
where for 
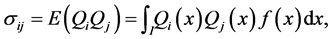 and may be expressed as
and may be expressed as
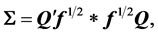
where 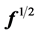 stands for the continuous diagonal matrix
stands for the continuous diagonal matrix 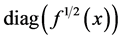 and the row × column multiplication, denoted by
and the row × column multiplication, denoted by ![]() is evaluated at
is evaluated at ![]() and then follows an integration w.r.t.
and then follows an integration w.r.t. 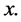
In the theorems below, 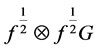 and
and  stands for
stands for 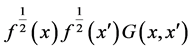 and
and 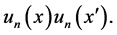
Theorem 2. Suppose that for a Euclidean distance ![]() the geometric variability
the geometric variability  is finite. Define
is finite. Define  Then:
Then:
1. 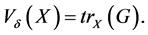
2.  is a Hilbert-Schmidt kernel, i.e.,
is a Hilbert-Schmidt kernel, i.e.,
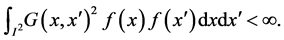
Proof. Let  be i.i.d. and write
be i.i.d. and write  From (7)
From (7) 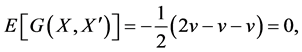 and hence using (8),
and hence using (8),
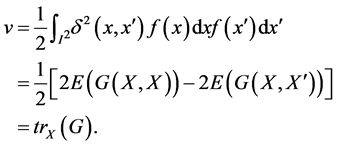
This proves 1). Next, ![]() is p.s.d., so for
is p.s.d., so for  the
the 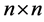 matrix with entries
matrix with entries  is p.s.d. In particular, for
is p.s.d. In particular, for ![]() with
with 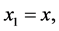
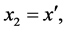 the determinant
the determinant

is non-negative. Thus

Integrating this inequality over ![]() gives
gives

and 2) is also proved. W Theorem 3. Suppose that 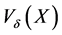 for a Euclidean distance
for a Euclidean distance ![]() is finite. Then the kernel
is finite. Then the kernel 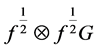 admits the expansion
admits the expansion
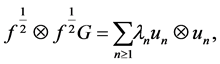 (9)
(9)
where 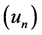 is a complete orthonormal set of eigenfunctions in
is a complete orthonormal set of eigenfunctions in . Let
. Let
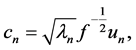 (10)
(10)
and  Then
Then 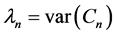 and
and  is a sequence of centered and uncorrelated r.v.’s, which are principal components of
is a sequence of centered and uncorrelated r.v.’s, which are principal components of  where
where 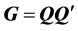 and
and
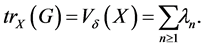
Proof. The eigendecomposition (9) exists because  is a Hilbert-Schmidt kernel and
is a Hilbert-Schmidt kernel and 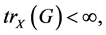 by Theorem 2. Next, (9) and (10) can be written as
by Theorem 2. Next, (9) and (10) can be written as
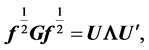 (11)
(11)
i.e., 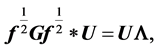 and
and 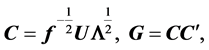 where
where 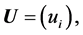
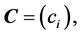
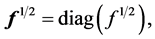
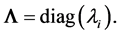 Thus, for all
Thus, for all 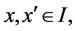
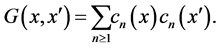
Next, for ![]() we have
we have 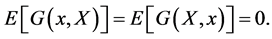 In particular, since
In particular, since
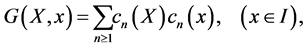
we have 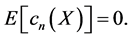 Moreover, from (10) we also have
Moreover, from (10) we also have
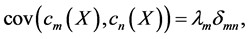
where  is Kronecker’s delta, showing that the variables
is Kronecker’s delta, showing that the variables 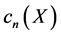 are centered and uncorrelated.
are centered and uncorrelated.
Recall the product matrix notation. The principal components of 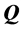 such that
such that 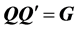 are
are 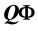 where
where
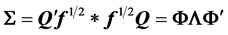 (12)
(12)
is the spectral decomposition of ![]() Premultiplying (12) by
Premultiplying (12) by 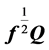 and postmultiplying by
and postmultiplying by ![]() we obtain
we obtain 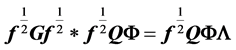 and therefore
and therefore
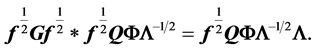
Thus the columns of  are eigenfunctions of
are eigenfunctions of  This shows that
This shows that  see
see
(11), and 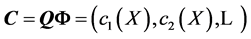 contains the principal components of
contains the principal components of 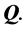 The rows in
The rows in ![]() may be accordingly called the principal coordinates of distance
may be accordingly called the principal coordinates of distance![]() . This name can be justified as follows.
. This name can be justified as follows.
Let us write the coordinates 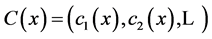 and suppose that
and suppose that 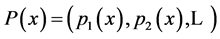 is another Euclidean configurations giving the same distance
is another Euclidean configurations giving the same distance![]() . The linear transformation
. The linear transformation 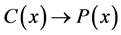 is orthogonal and
is orthogonal and 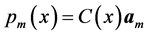 with
with  Then the r.v.’s
Then the r.v.’s  are uncorrelated and
are uncorrelated and
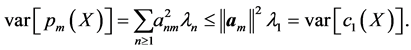
Thus 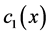 is the first principal coordinate in the sense that
is the first principal coordinate in the sense that  is maximum. The second coordinate
is maximum. The second coordinate  is orthogonal to
is orthogonal to 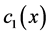 and has maximum variance, and so on with the others coordinates. W The following expansions hold as an immediate consequence of this theorem:
and has maximum variance, and so on with the others coordinates. W The following expansions hold as an immediate consequence of this theorem:
 (13)
(13)
 (14)
(14)
 (15)
(15)
where ![]() and
and 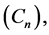
 , with
, with 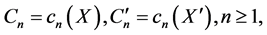 are sequences of centered and uncorrelated random variables, which are principal components of
are sequences of centered and uncorrelated random variables, which are principal components of . We next obtain some concrete expansions.
. We next obtain some concrete expansions.
4. A Particular Expansion
If ![]() is a continuous r.v. with finite mean and variance,
is a continuous r.v. with finite mean and variance, 
 say, and
say, and ![]() is the ordinary Euclidean distance
is the ordinary Euclidean distance , then it is easy to prove that
, then it is easy to prove that 
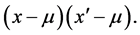 Then from (14) and taking
Then from (14) and taking  we obtain
we obtain 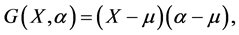 which provides the trivial expansion
which provides the trivial expansion ![]() A much more interesting expansion can be obtained by taking the square root of
A much more interesting expansion can be obtained by taking the square root of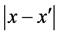 .
.
4.1. The Square Root Distance
Let us consider the distance function
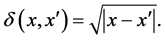 (16)
(16)
The double-centered inner product 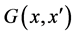 is next given.
is next given.
Definition 3. Let 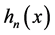 be defined as
be defined as  where
where 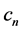 is defined in (10).
is defined in (10).
We immediately have the following result.
Proposition 1. The function ![]() satisfies:
satisfies:
1. 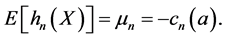
2. 
3. 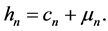
Proposition 2. Assuming 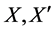 i.i.d., if
i.i.d., if , then
, then
 (17)
(17)
Proof. From 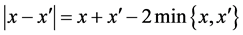 and combining (7) and (6), we obtain
and combining (7) and (6), we obtain 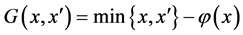
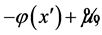 where
where 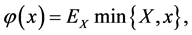 which satisfies
which satisfies 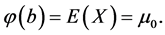
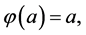 Hence
Hence 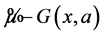
 and (17) holds. W Proposition 3. The following expansion holds
and (17) holds. W Proposition 3. The following expansion holds
 (18)
(18)
Proof. Using (17) and expanding  and setting
and setting 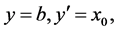 we get (18). W Replacing
we get (18). W Replacing 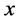 by
by ![]() we have the expansion
we have the expansion
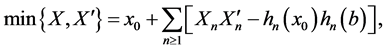 (19)
(19)
and, as a consequence [12]:
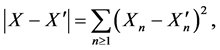
where ![]() is distributed as
is distributed as ![]() and
and 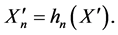 This expansion also follows from (15).
This expansion also follows from (15).
If 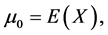
 from (19) we can also obtain the expansions
from (19) we can also obtain the expansions
 (20)
(20)
as well as
 (21)
(21)
where the convergence is in the mean square sense [27].
4.2. Principal Components
Related to the r.v. ![]() with cdf
with cdf  let us define the stochastic process
let us define the stochastic process 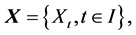 where
where 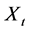 is the indicator of
is the indicator of  and follows the Bernoulli
and follows the Bernoulli  distribution with
distribution with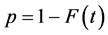 . For the distance (16), the relation between
. For the distance (16), the relation between![]() , the Bernoulli process
, the Bernoulli process 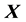 and
and ![]() is
is
 (22)
(22)
where 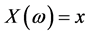 and
and  is a realization of X. Thus X is a continuous configuration for
is a realization of X. Thus X is a continuous configuration for ![]() Note that, if
Note that, if 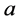 is finite, then
is finite, then
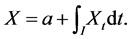
The covariance kernel 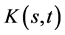 of X is given by
of X is given by  Let us consider the integral operator
Let us consider the integral operator ![]() with kernel
with kernel ![]()

where ![]() is an integrable function on
is an integrable function on  Let
Let  be the countable orthonormal set of eigenfunctions of
be the countable orthonormal set of eigenfunctions of  i.e.,
i.e., 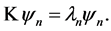 We may suppose that
We may suppose that 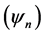 constitutes a basis of
constitutes a basis of  and the eigenvalues
and the eigenvalues 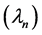 are arranged in descending order. As a consequence of Mercer’s theorem, the covariance kernel
are arranged in descending order. As a consequence of Mercer’s theorem, the covariance kernel  can be expanded as
can be expanded as
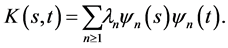 (23)
(23)
Theorem 4. The functions 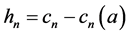 (see definition 3), satisfy:
(see definition 3), satisfy:
1. 
2. 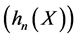 is a countable set of uncorrelated r.v.’s such that
is a countable set of uncorrelated r.v.’s such that 
3.  are principal coordinates for the distance
are principal coordinates for the distance  i.e.,
i.e.,
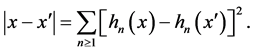
Proof. To prove 1), let us use the multiplication “*” and write  as
as 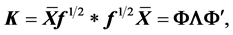 where
where
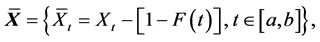
i.e., 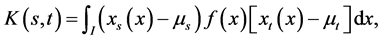 with
with 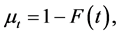 where
where 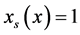 if
if 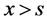 and 0 otherwise. Then
and 0 otherwise. Then 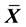 is a centered continuous configuration for
is a centered continuous configuration for ![]() and clearly
and clearly 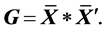 Arguing as in Theorem 3, the centered principal coordinates are
Arguing as in Theorem 3, the centered principal coordinates are  i.e.,
i.e.,
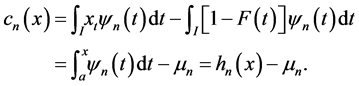
2) is a consequence of Theorem 3. An alternative proof follows by taking  in the formula for the covariance [28]:
in the formula for the covariance [28]:
 (24)
(24)
where  See Theorem 6.
See Theorem 6.
To prove 3), let 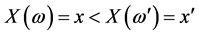 and
and 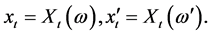 Then
Then  and
and 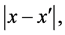 see (22), is
see (22), is

This proves that  are principal coordinates for the distance
are principal coordinates for the distance 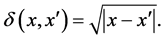 W The above results have been obtained via continuous scaling. For this particular distance, we get the same results by using the Karhunen-Loève (also called Kac-Siegert) expansion of X, namely,
W The above results have been obtained via continuous scaling. For this particular distance, we get the same results by using the Karhunen-Loève (also called Kac-Siegert) expansion of X, namely,
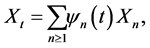 (25)
(25)
where 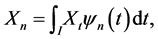 i.e.,
i.e., 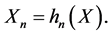 Thus each
Thus each 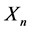 is a principal component of X and the sequence
is a principal component of X and the sequence  constitutes a countable set of uncorrelated random variables.
constitutes a countable set of uncorrelated random variables.
4.3. The Differential Equation
Let  where
where 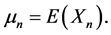 It can be proved [12] that the means
It can be proved [12] that the means 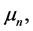 eigenvalues
eigenvalues ![]() and functions
and functions 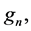 satisfy the second order differential equation
satisfy the second order differential equation
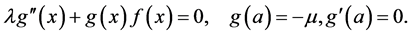 (26)
(26)
The solution of this equation is well-known when ![]() is
is 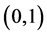 uniform.
uniform.
Examples of eigenfunctions 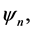 principal components
principal components 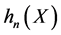 and the corresponding variances
and the corresponding variances ![]() are [12,27,29]:
are [12,27,29]:
1. ![]() is
is  uniform:
uniform: 
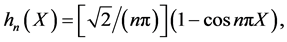
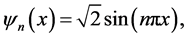
2. ![]() is exponential with unit mean. If
is exponential with unit mean. If 

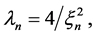 where
where ![]() is the n-th positive root of
is the n-th positive root of ![]() and
and 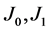 are the Bessel functions of the first order.
are the Bessel functions of the first order.
3. ![]() is standard logistic
is standard logistic 
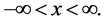 If
If 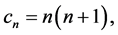

 (27)
(27)
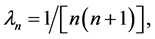 where
where  are the shifted Legendre polynomials on
are the shifted Legendre polynomials on 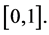
4. ![]() is Pareto with
is Pareto with 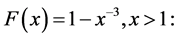
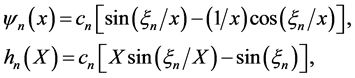
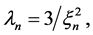 where
where
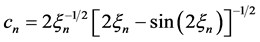
and 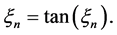
Note that the change of variable  transforms
transforms ![]() in
in  and (26) in
and (26) in
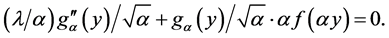
Hence 
 and
and  providing solutions for the variable
providing solutions for the variable  For instance, we immediately can obtain the principal dimensions of the Pareto distribution with cdf
For instance, we immediately can obtain the principal dimensions of the Pareto distribution with cdf 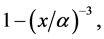
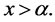
4.4. A Comparison
The results obtained in the previous sections can be compared and summarized in Table 1, where ![]() is a random variable with absolutely continuous cdf
is a random variable with absolutely continuous cdf 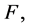 density
density 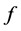 and support
and support  The continuous scaling expansion is found w.r.t. the distance (16). Note that we reach the same orthogonal expansions (we only include two), but this continuous scaling approach is more general, since by changing the distance we may find other
The continuous scaling expansion is found w.r.t. the distance (16). Note that we reach the same orthogonal expansions (we only include two), but this continuous scaling approach is more general, since by changing the distance we may find other
principal directions and expansions. This distance-based approach may be an alternative to the problem of finding nonlinear principal dimensions [30].
4.5. Some Properties of the Eigenfunctions
In this section we study some properties of the eigenfunctions  and their integrals
and their integrals 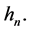
Proposition 4. The first eigenfunction ![]() is strictly positive and satisfies
is strictly positive and satisfies
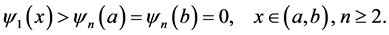
Proof. ![]() is positive, so
is positive, so ![]() is also positive (Perron-Frobenius theorem). On the other hand
is also positive (Perron-Frobenius theorem). On the other hand 
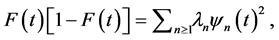 which satisfies
which satisfies  W Clearly, if
W Clearly, if ![]() is positive,
is positive, 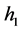 is increasing and positive. Moreover, any
is increasing and positive. Moreover, any ![]() satisfies the following bound.
satisfies the following bound.
Proposition 5. If 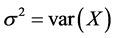 is finite then
is finite then 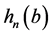 is also finite and
is also finite and
 (28)
(28)
Proof.  is an eigenfunction and from (24)
is an eigenfunction and from (24)
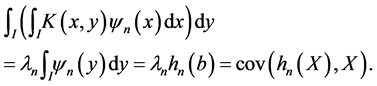
Hence 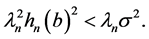 W Proposition 6. The principal components
W Proposition 6. The principal components 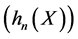 of
of  constitutes a complete orthogonal system of
constitutes a complete orthogonal system of 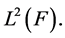
Proof. The orthogonality has been proved as a consequence of (24). Let  be a continuous function such that
be a continuous function such that 
![]() Suppose that
Suppose that 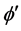 exists. As
exists. As 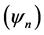 is a complete system
is a complete system  and integrating, we have
and integrating, we have 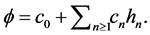 But
But 
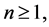 which shows that
which shows that  must be constant. W
must be constant. W
4.6. The First Principal Component
In this section we prove two interesting properties of  and the first principal component
and the first principal component  see [10].
see [10].
Proposition 7. The increasing function 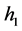 characterizes the distribution of
characterizes the distribution of ![]()
Proof. Write  Then
Then 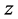 satisfies the differential equation (see (26))
satisfies the differential equation (see (26))
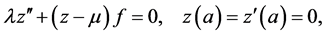 (29)
(29)
where 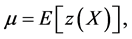
 When the function
When the function 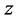 is given,
is given, ![]() and
and ![]() may be obtained by solving the equations
may be obtained by solving the equations

and the density of ![]() is
is 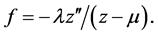 W Proposition 8. For a fixed
W Proposition 8. For a fixed 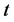 let
let 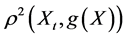 denote the squared correlation between
denote the squared correlation between  and a function
and a function 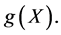 The average of
The average of 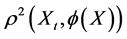 weighted by
weighted by 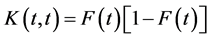 is maximum for
is maximum for  i.e.,
i.e.,

Proof. Let us write (see Proposition 6) 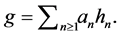 Then
Then  and we can suppose
and we can suppose 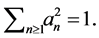 From (25)
From (25)
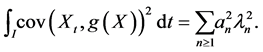
As  we have
we have
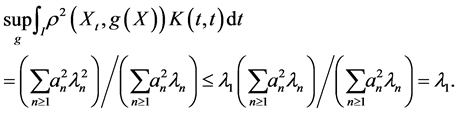
Thus the supreme is attained at  W
W
5. An Inequality
The following inequality holds for ![]() with the normal
with the normal 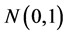 distribution [31,32]:
distribution [31,32]:
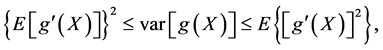
where ![]() is an absolutely continuous function and
is an absolutely continuous function and 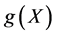 has finite variance. This inequality has been extended to other distributions by Klaassen [33]. Let us prove a related inequality concerning the function of a random variable and its derivative.
has finite variance. This inequality has been extended to other distributions by Klaassen [33]. Let us prove a related inequality concerning the function of a random variable and its derivative.
If  is the first principal dimension, then
is the first principal dimension, then 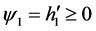 and
and 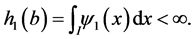 We can define the probability density
We can define the probability density 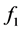 with support
with support  given by
given by
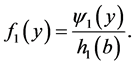
Theorem 5. Let 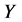 be a r.v. with pdf
be a r.v. with pdf 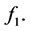 If
If ![]() is an absolutely continuous function and
is an absolutely continuous function and 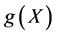 has finite variance, the following inequality holds
has finite variance, the following inequality holds
 (30)
(30)
with equality if ![]() is
is 
Proof. From Proposition 6, we can write 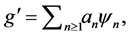 where
where  Then
Then 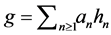 and
and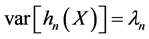 , so
, so
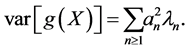
From Parseval’s identity 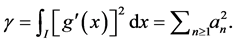 Thus we have
Thus we have
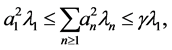
proving (30). Moreover, if  we have
we have  and
and  W Inequality (30) is equivalent to
W Inequality (30) is equivalent to
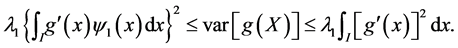 (31)
(31)
Some examples are next given.
5.1. Uniform Distribution
Suppose ![]() uniform
uniform  Then
Then 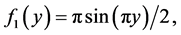
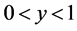 and
and 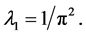 We obtain
We obtain
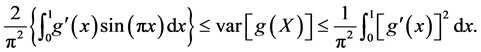
5.2. Exponential Distribution
Suppose ![]() exponential with mean 1. Then
exponential with mean 1. Then 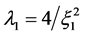 and
and
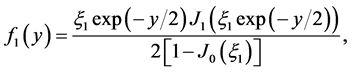
where  satisfies
satisfies 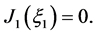 Inequality (31) is
Inequality (31) is
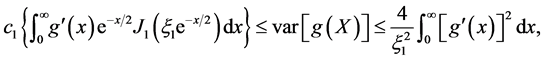
where 
5.3. Pareto Distribution
Suppose ![]() with density
with density 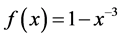 for
for ![]() Then
Then 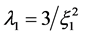 and
and
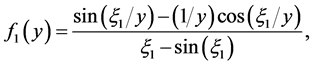
where 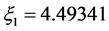 satisfies
satisfies 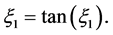 Inequality (31) is
Inequality (31) is
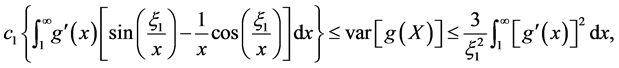
where 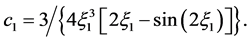
5.4. Logistic Distribution
Suppose that ![]() follows the standard logistic distribution. The cdf is
follows the standard logistic distribution. The cdf is

and the density is 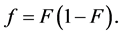
This distribution has especial interest, as the two first principal components are  i.e., proportional to the cdf and the density, respectively. Note that
i.e., proportional to the cdf and the density, respectively. Note that 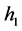 can be obtained directly, as if we write
can be obtained directly, as if we write  then
then 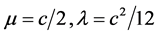 and (29) gives
and (29) gives
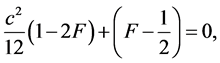
so  Similarly, we can obtain
Similarly, we can obtain 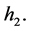 Besides
Besides
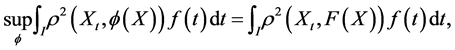
i.e., the expectation of 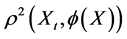 w.r.t.
w.r.t. 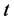 with density
with density 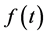 is maximum for
is maximum for 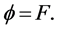
Now  and
and 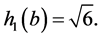 The density
The density 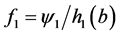 is just
is just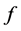 , therefore inequality (30) for the logistic distribution reduces to
, therefore inequality (30) for the logistic distribution reduces to
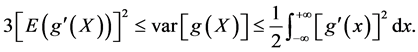
In general, if 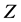 is logistic with variance
is logistic with variance 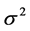 then
then ![]() with
with 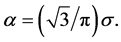 Noting that the functions
Noting that the functions 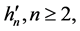 are orthogonal to
are orthogonal to 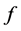 and using (24), we obtain
and using (24), we obtain
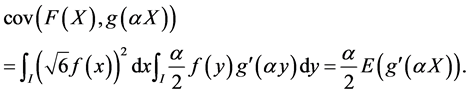
As  the Cauchy-Schwarz inequality proves that
the Cauchy-Schwarz inequality proves that
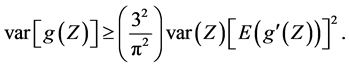
6. Diagonal Expansions
Correspondence analysis is a variant of multidimensional scaling, used for representing the rows and columns of a contingency table, as points in a space of low-dimension separated by the chi-square distance. See [15,34]. This method employs a singular value decomposition (SVD) of a transformed matrix. A continuous scaling expansion, viewed as a generalization of correspondence analysis, can be obtained from (3) and (4).
6.1. Univariate Case
Let 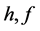 be two densities with the same support
be two densities with the same support ![]() Define the squared distance
Define the squared distance
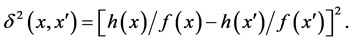
The double-centered inner product is given by
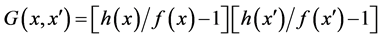
and the geometric variability is
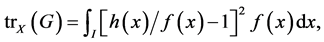
which is a Pearson measure of divergence between 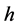 and
and ![]() If
If  is an orthonormal basis for
is an orthonormal basis for 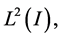 we may consider the expansion
we may consider the expansion

and defining 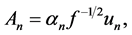 then
then

and
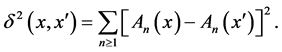
However, 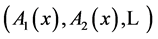 are not the principal coordinates related to the above distance. In fact, the continuous scaling dimension is 1 for this distance and it can be found in a straightforward way.
are not the principal coordinates related to the above distance. In fact, the continuous scaling dimension is 1 for this distance and it can be found in a straightforward way.
6.2. Bivariate Case
Let us write (4) as
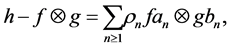 (32)
(32)
where 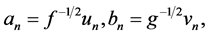
 are the canonical functions and
are the canonical functions and  is the sequence of canonical correlations. Note that
is the sequence of canonical correlations. Note that 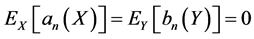 and
and 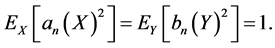
Suppose that  is absolutely continuous w.r.t.
is absolutely continuous w.r.t. 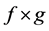 and let us consider the Radom-Nikodym derivative
and let us consider the Radom-Nikodym derivative
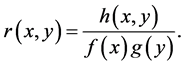
The so-called chi-square distance between  is given by
is given by
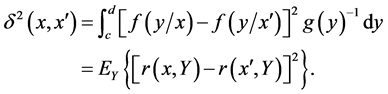
Let 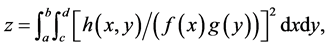 the Pearson contingency coefficient is defined by
the Pearson contingency coefficient is defined by

The geometric variability of the chi-square distance is 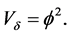 In fact
In fact
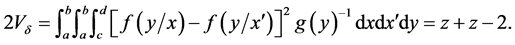
The proximity function is
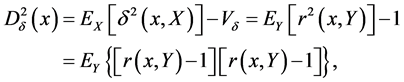
and the double-centered inner product is

We can express (32) as
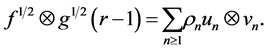
This SVD exists provided that 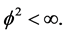 Multiplying
Multiplying 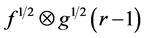 by himself and integrating w.r.t.
by himself and integrating w.r.t. ![]() we readily obtain
we readily obtain

Comparing with (9) we have the principal coordinates 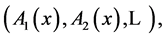 where
where 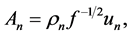 which satisfy
which satisfy
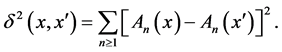
Then
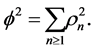
See [18] for further details.
Finally, the following expansion in terms of cdf’s holds [35]:
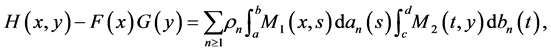 (33)
(33)
where 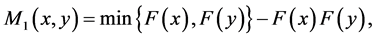
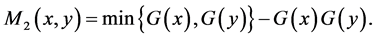 Using a matrix notation, this diagonal expansion can be written as
Using a matrix notation, this diagonal expansion can be written as

where 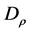 stands for the diagonal matrix with the canonical correlations, and
stands for the diagonal matrix with the canonical correlations, and 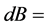

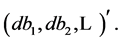
7. The Covariance between Two Functions
Here we generalize the well-known Hoeffding’s formula
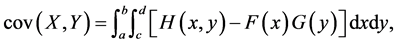
which provides the covariance in terms of the bivariate and univariate cdf’s. The proof of the generalization below uses Fubini’s theorem and integration by parts, being different from the proof given in [28].
Let us suppose that the supports of 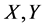 are the intervals
are the intervals 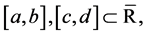 respectively, although the results may also hold for other subsets of
respectively, although the results may also hold for other subsets of ![]() We then have
We then have
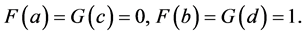
Theorem 6. If 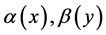 are two functions defined on
are two functions defined on  respectively, such that:
respectively, such that:
1. Both functions are of bounded variation.
2. 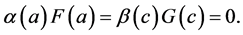
3. The expectations 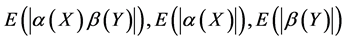 are finite.
are finite.
Then:
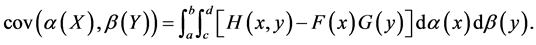 (34)
(34)
Proof. The covariance exists and is

where 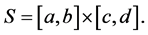 Integration by parts gives
Integration by parts gives
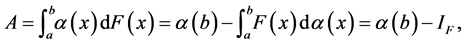
and similarly 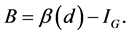 By Fubini’s theorem for transition probabilities
By Fubini’s theorem for transition probabilities

where 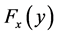 is the cdf of
is the cdf of 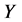 given
given![]() , we can write
, we can write

We first integrate with respect to ![]() Setting
Setting 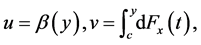 to find
to find 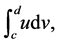 integration by parts gives
integration by parts gives
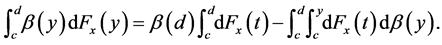
Since 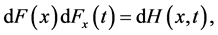 setting
setting 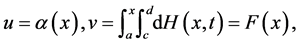 we find
we find

and setting 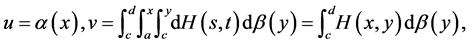 again integration by parts gives
again integration by parts gives

where  Therefore
Therefore
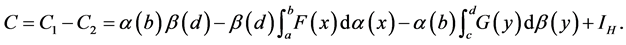
A last simplification shows that 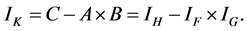 W
W
8. Canonical Analysis
Given two sets of variables, the purpose of canonical correlation analysis is to find sets of linear combinations with maximal correlation. In Section 6.2 we studied, from a multidimensional scaling perspective, the nonlinear canonical functions of ![]() and
and ![]() with joint pdf
with joint pdf 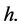 Here we find the canonical correlations and functions for several copulas.
Here we find the canonical correlations and functions for several copulas.
Let  be a bivariate random vector with cdf
be a bivariate random vector with cdf , where
, where ![]() and
and ![]() are
are 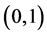 uniform. Then
uniform. Then ![]() is a cdf called copula [36]. Let us suppose
is a cdf called copula [36]. Let us suppose ![]() symmetric. Then
symmetric. Then  Therefore, in finding the canonical functions, we can suppose
Therefore, in finding the canonical functions, we can suppose 
Let us consider the symmetric kernels
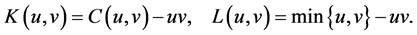
We seek the canonical functions 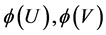 and the corresponding canonical correlations, i.e.,
and the corresponding canonical correlations, i.e.,
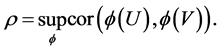 (35)
(35)
Definition 4. A generalized eigenfuction of ![]() w.r.t.
w.r.t.  with eigenvalue
with eigenvalue ![]() is a function
is a function ![]() such that
such that
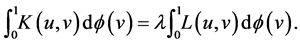 (36)
(36)
From the theory of integral equations, we have
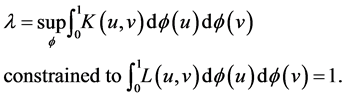 (37)
(37)
Definition 5. On the set of functions in 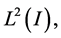 with
with 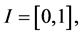 we define the inner products
we define the inner products
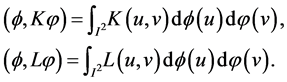
Clearly, see Theorem 6, if 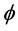 is eigenfunction of
is eigenfunction of ![]() w.r.t.
w.r.t. 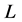 with eigenvalue
with eigenvalue ![]() we have the covariance
we have the covariance 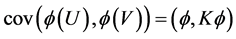 and the variance
and the variance 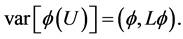 Therefore the correlation between
Therefore the correlation between 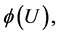
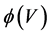 is:
is:

Thus the canonical correlations of  are the eigenvalues of
are the eigenvalues of ![]() w.r.t.
w.r.t. ![]()
Justified by the embedding in a Euclidean or Hilbert space via the chi-square distance, the geometric dimension of a copula ![]() is defined as the cardinal of the set
is defined as the cardinal of the set  of canonical correlations. The dimension can be finite, infinite countable (cardinality of
of canonical correlations. The dimension can be finite, infinite countable (cardinality of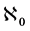 ) or uncountable (cardinality of the continuum
) or uncountable (cardinality of the continuum![]() ).
).
We next illustrate these results with some copulas. Since 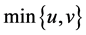 is a copula, the so-called FréchetHoeffding upper bound, we firstly suggest a procedure for constructing copulas and performing canonical analysis. This procedure is based on the expansion (23) for the logistic distribution.
is a copula, the so-called FréchetHoeffding upper bound, we firstly suggest a procedure for constructing copulas and performing canonical analysis. This procedure is based on the expansion (23) for the logistic distribution.
For this distribution, if 
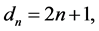 we have [27]:
we have [27]:
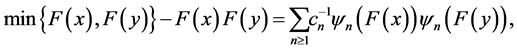
where  is given in (27). With the change
is given in (27). With the change 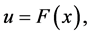
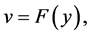 we find:
we find:
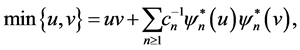 (38)
(38)
with  and
and
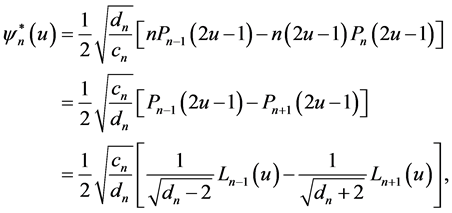
where ![]() are Legendre polynomials and
are Legendre polynomials and 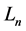 are shifted Legendre polynomials on
are shifted Legendre polynomials on . Thus
. Thus 

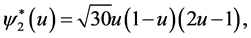
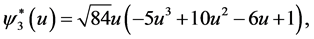 etc.
etc.
8.1. FGM Copula
If we consider only 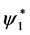 in (38), we obtain the Farlie-Gumbel-Morgenstern copula:
in (38), we obtain the Farlie-Gumbel-Morgenstern copula:

Then 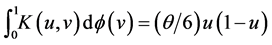 and
and 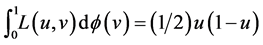 if
if 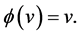 Thus
Thus ![]() is an eigenfunction with eigenvalue
is an eigenfunction with eigenvalue  Then
Then 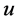 and
and ![]() are the canonical functions with canonical correlation
are the canonical functions with canonical correlation  The geometric dimension is one.
The geometric dimension is one.
8.2. Extended FGM Copula
By taking more terms in expansion (38), we may consider the following copula

where  The canonical correlations are
The canonical correlations are  The canonical functions are
The canonical functions are 
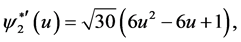
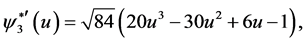 respectively. This copula has dimension 3.
respectively. This copula has dimension 3.
Clearly 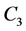 reduces to the FGM copula if
reduces to the FGM copula if  When the dimension is 2, i.e.,
When the dimension is 2, i.e., 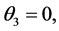 we have a copula with cubic sections [37]. A generalization is given in [38].
we have a copula with cubic sections [37]. A generalization is given in [38].
8.3. Cuadras-Augé Copula
The Cuadras-Augé family of copulas [39] is defined as the weighted geometric mean of  and
and 

For this copula, the canonical correlations constitute a continuous set. If 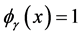 for
for ![]() and 0 otherwise, it can be proved [40] that the set
and 0 otherwise, it can be proved [40] that the set 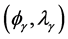 of eigenpairs of
of eigenpairs of 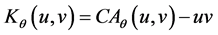 w.r.t.
w.r.t. 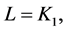 is given by
is given by
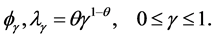
Thus, the set of canonical functions and correlations for the Cuadras-Augé copula is the uncountable set 
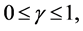 with dimension of the power of the continuum. In particular, the maximum correlation is the parameter
with dimension of the power of the continuum. In particular, the maximum correlation is the parameter ![]() with canonical function the Heaviside distribution
with canonical function the Heaviside distribution  The maximum correlation
The maximum correlation ![]() was obtained by Cuadras [28].
was obtained by Cuadras [28].
[1] REFERENCES
[2] T. W. Anderson and M. A. Stephens, “The Continuous and Discrete Brownian Bridges: Representation and Applications,” Linear Algebra and Its Applications, Vol. 264, 1996, pp. 145-171. http://dx.doi.org/10.1016/S0024-3795(97)00015-3
[3] J. Durbin and M. Knott, “Components of Cramér-von Mises Statistics. I,” Journal of the Royal Statistical Society: Series B, Vol. 34, 1972, pp. 290-307.
[4] J. Fortiana and C. M. Cuadras, “A Family of Matrices, the Discretized Brownian Bridges and Distance-Based Regression,” Linear Algebra and Its Applications, Vol. 264, 1997, pp. 173-188. http://dx.doi.org/10.1016/S0024-3795(97)00051-7
[5] J. L. Doob, “Stochastic Processes,” Wiley, New York, 1953.
[6] M. Loève, “Probability Theory,” 3rd Edition, Van Nostrand, Princeton, 1963.
[7] G. K. Eagleson, “Orthogonal Expansions and U-Statistics,” Australian Journal of Statistics, Vol. 21, No. 3, 1979, pp. 221-237. http://dx.doi.org/10.1111/j.1467-842X.1979.tb01141.x
[8] C. M. Cuadras and D. Cuadras, “Orthogonal Expansions and Distinction between Logistic and Normal,” In: C. Huber-Carol, N. Balakrishnan, M. S. Nikulin and M. Mesbah, Eds., Goodness-Of-Fit Tests and Model Validity, Birkhäuser, Boston, 2002, pp. 327-339. http://dx.doi.org/10.1007/978-1-4612-0103-8_24
[9] J. Fortiana and A. Grané, “Goodness-Of-Fit Tests Based on Maximum Correlations and Their Orthogonal Decompositions,” Journal of the Royal Statistical Society: Series B, Vol. 65, No. 1, 2003, pp. 115-126. http://dx.doi.org/10.1111/1467-9868.00375
[10] C. M. Cuadras, “Diagonal Distributions via Orthogonal Expansions and Tests of Independence,” In: C. M. Cuadras, J. Fortiana and J. A. Rodriguez-Lallena, Eds., Distributions with Given Marginals and Statistical Modelling, Kluwer Academic Press, Dordrecht, 2002, pp. 35-42. http://dx.doi.org/10.1007/978-94-017-0061-0_5
[11] C. M. Cuadras, “First Principal Component Characterization of a Continuous Random Variable,” In: N. Balakrishnan, I. G. Bairamov and O. L. Gebizlioglu, Eds., Advances on Models, Characterizations and Applications, Chapman and Hall/CRC, London, 2005, pp. 189-199. http://dx.doi.org/10.1201/9781420028690.ch12
[12] C. M. Cuadras and J. Fortiana, “Continuous Metric Scaling and Prediction,” In: C. M. Cuadras and C. R. Rao, Eds., Multivariate Analysis, Future Directions 2, Elsevier Science Publishers B. V. (North-Holland), Amsterdam, 1993, pp. 47-66.
[13] C. M. Cuadras and J. Fortiana, “A Continuous Metric Scaling Solution for a Random Variable,” Journal of Multivariate Analysis, Vol. 52, No. 1, 1995, pp. 1-14. http://www.sciencedirect.com/science/article/pii/S0047259X85710019 http://dx.doi.org/10.1006/jmva.1995.1001
[14] C. M. Cuadras and J. Fortiana, “Weighted Continuous Metric Scaling,” In: A. K. Gupta and V. L. Girko, Eds., Multidimensional Statistical Analysis and Theory of Random Matrices, VSP, Zeist, 1996, pp. 27-40.
[15] C. M. Cuadras and J. Fortiana, “The Importance of Geometry in Multivariate Analysis and Some Applications,” In: C. R. Rao and G. Szekely, Eds., Statistics for the 21st Century, Marcel Dekker, New York, 2000, pp. 93-108.
[16] C. M. Cuadras and D. Cuadras, “A Parametric Approach to Correspondence Analysis,” Linear Algebra and Its Applications, Vol. 417, No. 1, 2006, pp. 64-74. http://www.sciencedirect.com/science/article/pii/S0024379505005203 http://dx.doi.org/10.1016/j.laa.2005.10.029
[17] C. M. Cuadras and D. Cuadras, “Eigenanalysis on a Bivariate Covariance Kernel,” Journal of Multivariate Analysis, Vol. 99, No. 10, 2008, pp. 2497-2507. http://www.sciencedirect.com/science/article/pii/S0047259X08000754 http://dx.doi.org/10.1016/j.jmva.2008.02.039
[18] H. O. Lancaster, “The Chi-Squared Distribution,” Wiley, New York, 1969.
[19] C. M. Cuadras, J. Fortiana and M. J. Greenacre, “Continuous Extensions of Matrix Formulations in Correspondence Analysis, with Applications to the FGM Family of Distributions,” In: R. D. H. Heijmans, D. S. G. Pollock and A. Satorra, Eds., Innovations in Multivariate Statistical Analysis, Kluwer Academic Publisher, Dordrecht, 2000, pp. 101-116. http://dx.doi.org/10.1007/978-1-4615-4603-0_7
[20] C. M. Cuadras, J. Fortiana and F. Oliva, “The Proximity of an Individual to a Population with Applications in Discriminant Analysis,” Journal of Classification, Vol. 14, No. 1, 1997, pp. 117-136. http://dx.doi.org/10.1007/s003579900006
[21] K. V. Mardia, J. T. Kent and J. M. Bibby, “Multivariate Analysis,” Academic Press, London, 1979.
[22] T. F. Cox and M. A. Cox, “Multidimensional Scaling,” Chapman and Hall, London, 1994.
[23] I. J. Schoenberg, “Remarks to Maurice Fréchet’s Article ‘Sur la définition axiomtique d’une classe d’espaces vectoriels distanciés applicables vectoriellment sur l’espace de Hilbert’,” Annals of Mathematics, Vol. 36, No. 3, 1935, pp. 724-732. http://dx.doi.org/10.2307/1968654
[24] C. M. Cuadras, “Distance Analysis in Discrimination and Classification Using Both Continuous and Categorical Variables,” In: Y. Dodge, Ed., Statistical Data Analysis and Inference, Elsevier Science Publishers B. V. (North-Holland), Amsterdam, 1989, pp. 459-473.
[25] C. M. Cuadras, E. A. Atkinson and J. Fortiana, “Probability Densities from Distances and Discriminant Analysis,” Statistics and Probability Letters, Vol. 33, No. 4, 1997, pp. 405-411. http://dx.doi.org/10.1016/S0167-7152(96)00154-X
[26] C. R. Rao, “Diversity: Its Measurement, Decomposition, Apportionment and Analysis,” Sankhyā: The Indian Journal of Statistics, Series A, Vol. 44, No. 1, 1982, pp. 1-21.
[27] Z. Liu and C. R. Rao, “Asymptotic Distribution of Statistics Based on Quadratic Entropy and Bootstrapping,” Journal of Statistical Planning and Inference, Vol. 43, No. 1-2, 1995, pp. 1-18. http://dx.doi.org/10.1016/0378-3758(94)00005-G
[28] C. M. Cuadras and Y. Lahlou, “Some Orthogonal Expansions for the Logistic Distribution,” Communications in Statistics— Theory and Methods, Vol. 29, No. 12, 2000, pp. 2643-2663. http://dx.doi.org/10.1080/03610920008832629
[29] C. M. Cuadras, “On the Covariance between Functions,” Journal of Multivariate Analysis, Vol. 81, No. 1, 2002, pp. 19-27. http://www.sciencedirect.com/science/article/pii/S0047259X01920007 http://dx.doi.org/10.1006/jmva.2001.2000
[30] C. M. Cuadras and Y. Lahlou, “Principal Components of the Pareto Distribution,” In: C. M. Cuadras, J. Fortiana and J. A. Rodriguez-Lallena, Eds., Distributions with Given Marginals and Statistical Modelling, Kluwer Academic Press, Dordrecht, 2002, pp. 43-50. http://dx.doi.org/10.1007/978-94-017-0061-0_6
[31] E. Salinelli, “Nonlinear Principal Components, II: Characterization of Normal Distributions,” Journal of Multivariate Analysis, Vol. 100, No. 4, 2009, pp. 652-660. http://dx.doi.org/10.1016/j.jmva.2008.07.001
[32] H. Chernoff, “A Note on an Inequality Involving the Normal Distribution,” Annals of Probability, Vol. 9, No. 3, 1981, pp. 533-535. http://dx.doi.org/10.1214/aop/1176994428
[33] T. Cacoullos, “On Upper and Lower Bounds for the Variance of a Function of a Random Variable,” Annals of Probability, Vol. 10, No. 3, 1982. pp. 799-809. http://dx.doi.org/10.1214/aop/1176993788
[34] C. A. J. Klaassen, “On an Inequality of Chernoff,” Annals of Probability, Vol. 13, No. 3, 1985, pp. 966-974. http://dx.doi.org/10.1214/aop/1176992917
[35] M. J. Greenacre, “Theory and Applications of Correspondence Analysis,” Academic Press, London, 1984.
[36] C. M. Cuadras, “Correspondence Analysis and Diagonal Expansions in Terms of Distribution Functions,” Journal of Statistical Planning and Inference, Vol. 103, No. 1-2, 2002, pp. 137-150. http://dx.doi.org/10.1016/S0378-3758(01)00216-6
[37] R. B. Nelsen, “An Introduction to Copulas,” 2nd Edition, Springer, New York, 2006.
[38] R. B. Nelsen, J. J. Quesada-Molina and J. A. Rodriguez-Lallena, “Bivariate Copulas with Cubic Sections,” Journal of Nonparametric Statistics, Vol. 7, No. 3, 1997, pp. 205-220. http://dx.doi.org/10.1080/10485259708832700
[39] C. M. Cuadras and W. Daz, “Another Generalization of the Bivariate FGM Distribution with Two-Dimensional Extensions,” Acta et Commentationes Universitatis Tartuensis de Mathematica, Vol. 16, No. 1, 2012, pp. 3-12. http://math.ut.ee/acta/16-1/CuadrasDiaz.pdf
[40] C. M. Cuadras and J. Augé, “A Continuous General Multivariate Distribution and Its Properties,” Communications in Statistics—Theory and Methods, Vol. 10, No. 4, 1981, pp. 339-353. http://dx.doi.org/10.1080/03610928108828042
[41] C. M. Cuadras, “Continuous Canonical Correlation Analysis,” Research Letters in the Information and Mathematical Sciences, Vol. 8, 2005, pp. 97-103. http://muir.massey.ac.nz/handle/10179/4454


