ABSTRACT

Geographically weighted regression models with the measurement error are a modeling method that combines the global regression models with the measurement error and the weighted regression model. The assumptions used in this model are a normally distributed error with that the expectation value is zero and the variance is constant. The purpose of this study is to estimate the parameters of the model and find the properties of these estimators. Estimation is done by using the Weighted Least Squares (WLS) which gives different weighting to each location. The variance of the measurement error is known. Estimators obtained are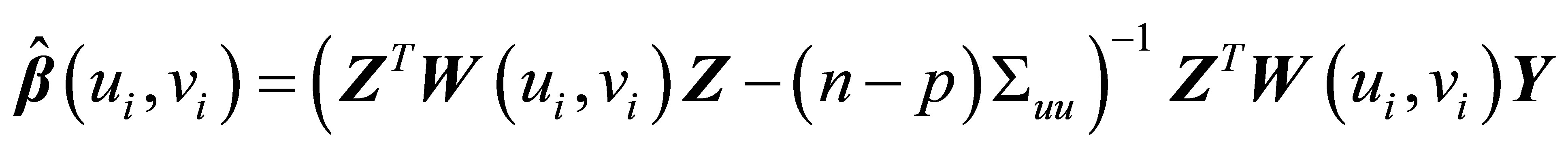. The properties of the estimator are unbiased and have a minimum variance.

1. Introduction

The measurement error is the error appeared when a recorded value isn’t exactly equal to the true value in terms of a measurement process, so that the true value of the explanatory variables is represented by a value that is obtained through a measurement process that isn’t necessarily correspond to the true value.

[1] says that the measurement errors affect the slope of the regression curve. [2] say that the measurement errors can lead to bias in the regression estimator and also lead to a model that is not built right or not representative of the population. The presence of the measurement error causes biased and inconsistent parameter estimates and leads to erroneous conclusions [3]. In addressing these issues, we use the measurement error models.

There are many researches that have been discussed about parametric regression models with the measurement error, including [2,4]. Nonparametric regression models with the measurement errors have been developed by [5]. They discussed a nonparametric regression function estimator which is constructed to reflect the fact that there are errors in variables. The result of their study shows that the convergence rates of all possible estimators have a lower bound possessed by the kernel estimators. In addition, [6] have conducted a study to estimate the parameters in the measurement error model with the modified spline method.

Some researches have been done on the nonlinear regression model with the measurement errors such as [7] in the logistic regression model of the development of heart disease. In their study, they introduced a bias-adjusted estimator. [8] conducted a study of the measurement error in the generalized linear model (GLM). The results of the computational methods offered an informative plot, called the measurement error trace which graphically illustrates the effect of the measurement error on the estimated parameters. [9] estimated the parameters of the proportional hazard models.

According to [10], spatial data are prone to the measurement error in the covariates, so that the research for spatial regression models with the measurement errors begins to develop, because in practice there are variables that can’t be measured directly or can’t be measured precisely in accordance with the true value as well as the spatial effect. [10] used a model of the conditional auto-regressive (CAR) in the study of spatial linear mixed model. The results of their research show that the naive estimators of the regression coefficients are attenuated while the naive estimators of the variance components are inflated, if the measurement error is ignored.

Beside CAR, there are several ways to analyze the spatial data. One of them is the geographically weighted regression model [11]. The geographically weighted regression model (GWR) is a development of the classical linear regression model. In the linear regression model only valid parameter estimators are produced globally, whereas in the GWR model it produced the model parameter estimators that are local to each observation location.

Based on the problems and the development of the research before, in this case, we are interested in examining the GWR model with the measurement error. So that, the purpose of this study is to determine the parameter estimators β and to examine the statistical properties of the resulting on the GWR model with the measurement error.

2. Model

GWR Model is a regression model of global development of the basic idea which is taken from the nonparametric regression [12]. This Model is a locally linear regression that generates a local model parameter estimates to each point or the region where the data is collected.

GWR Model can be written as follows [11]:

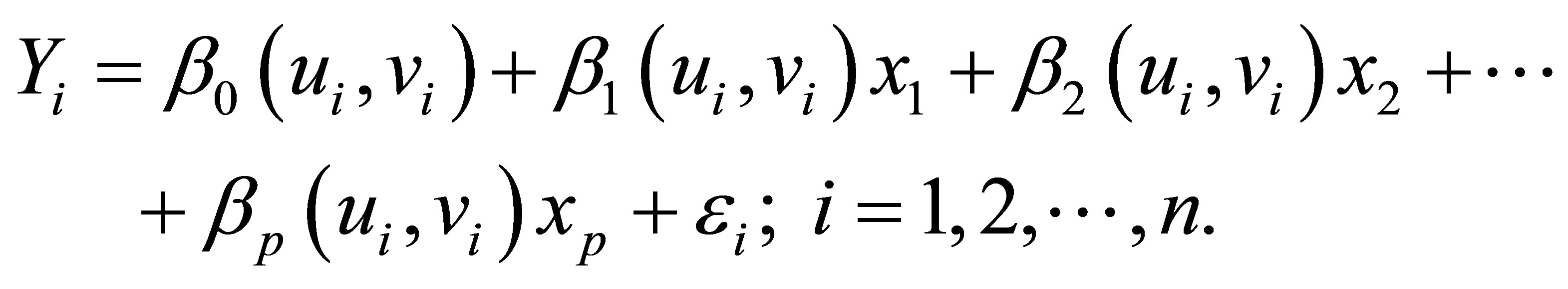(2.1)

with 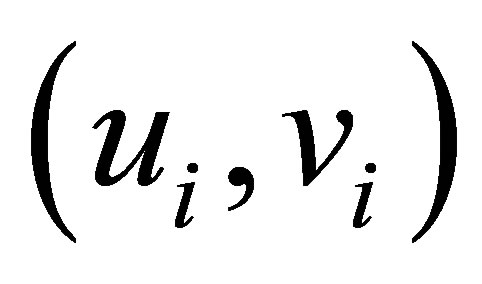states the point of coordinates (latitude, longitude) region is the value of a random variable and x_i is the value of a fixed variable which is known and does not contain errors. This means that x_i can be observed directly.

If x_i can’t be observed directly, it will be observed variables z_i. In this case, there has been a measurement error of the x_i. Measurement error is referred to as an error on the variables x_i. Measurement error models are:

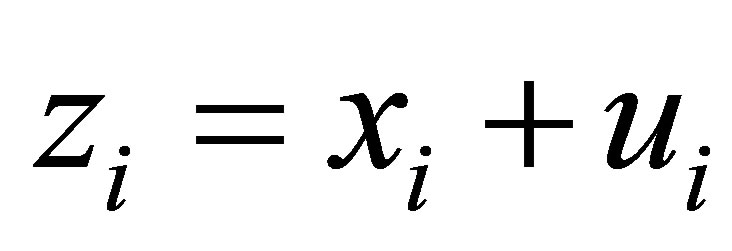(2.2)

where 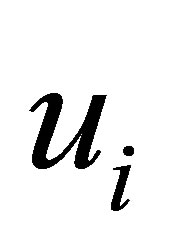is a random variables. The observed random variables called indicator variables, and unobserved variables 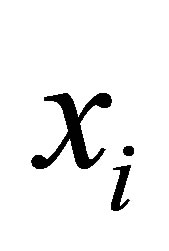referred to as latent variables.

So that from Equations (2.1) and (2.2) the regression model becomes:

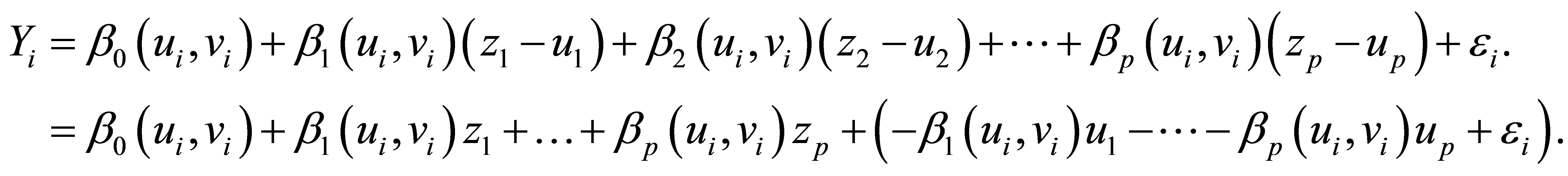
3. Estimation

The first step from this model approach is forming a weighting matrix for each observation (location). Weighting matrix is used to estimate the parameters in the location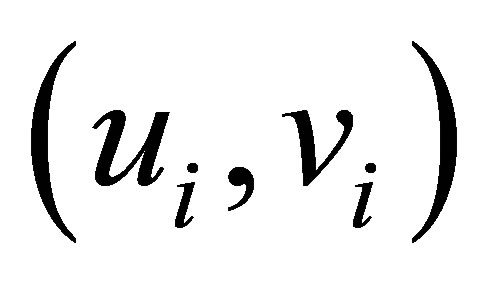. Suppose the weight for each location

is, , then the location parameter allegedly by adding the element weighting 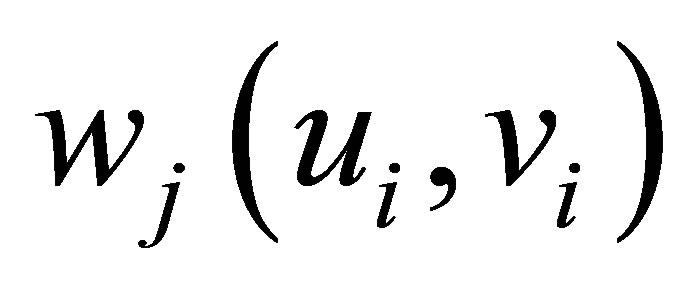in Equation (2.1).

(3.1)

Suppose is the element of the i-th row of the matrix 𝑿. Then the value of y at the location of the observation 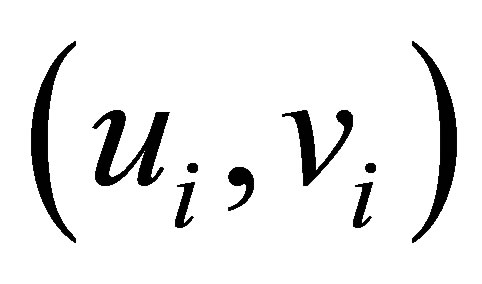can be written as follows:

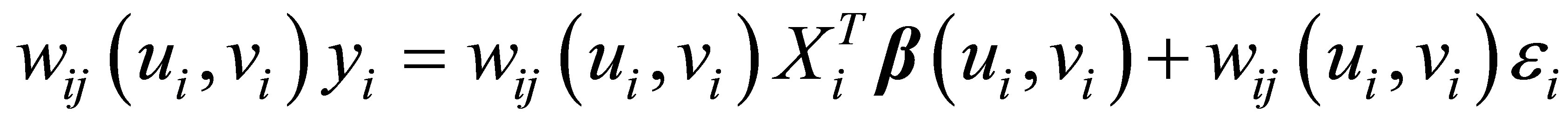
We let 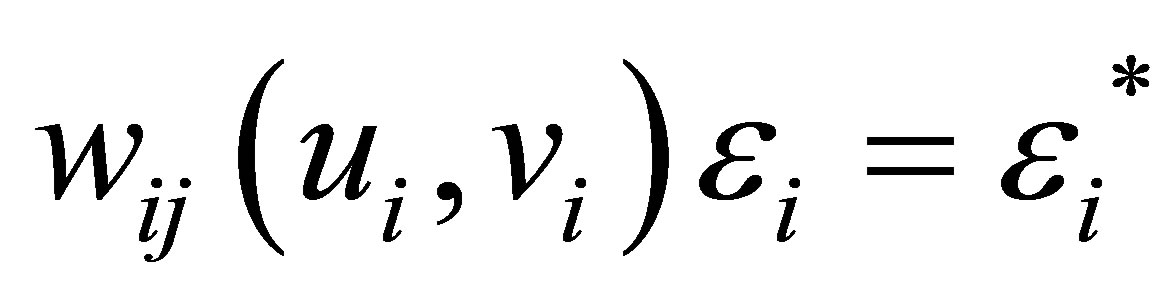then

, (3.2)

If 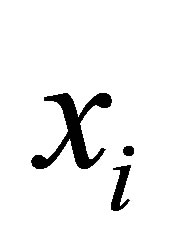can’t be directly observed or experienced 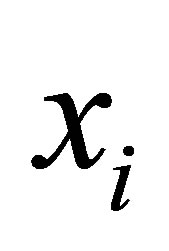measurement error, then the Equation (3.1) becomes:

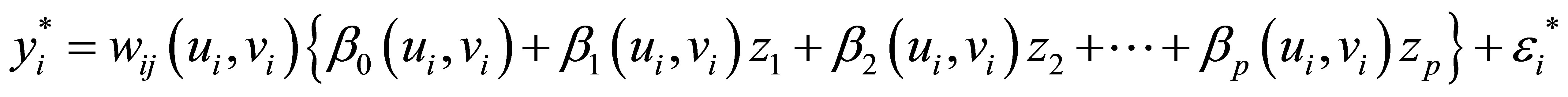
In Equation (3.2) it is assumed that has mean 0 and constant variance.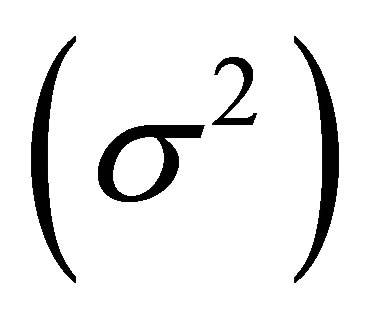

Means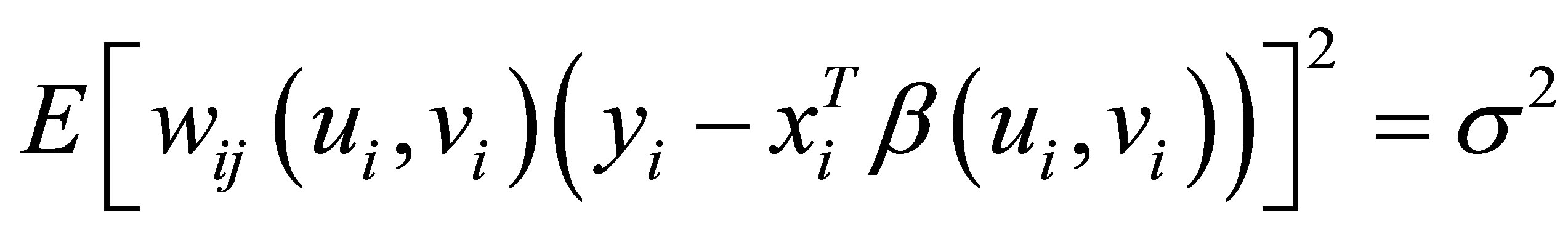, so that

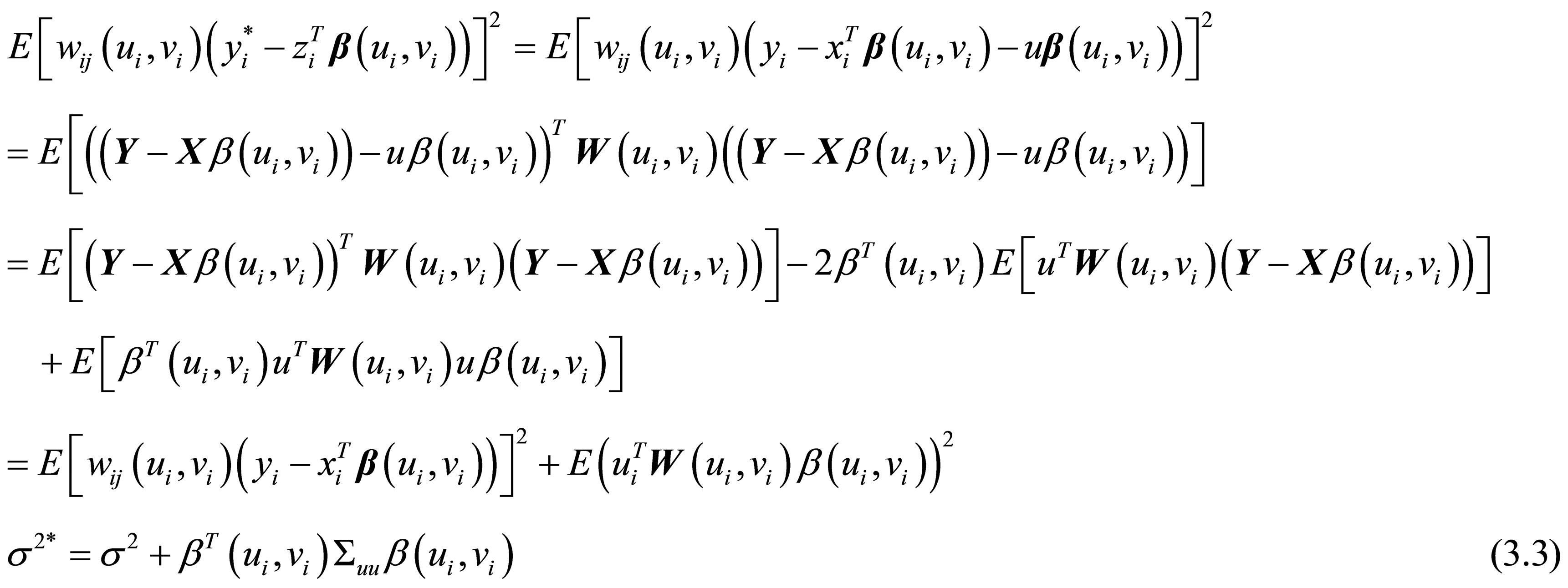
where

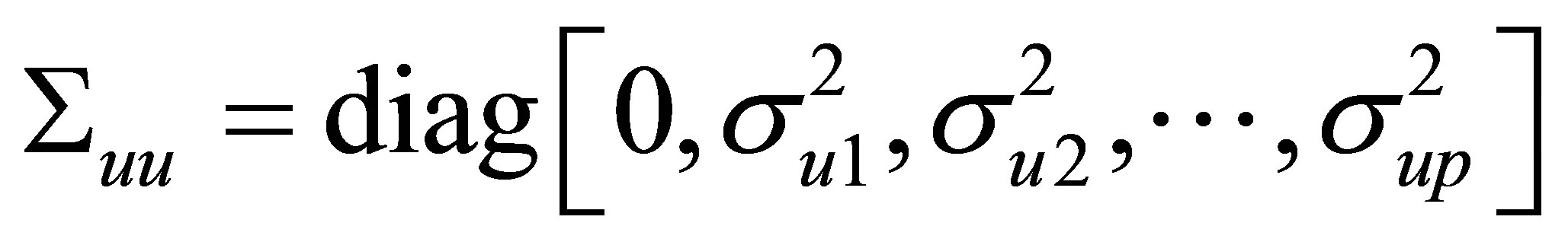
From Equation (3.3) with

^,

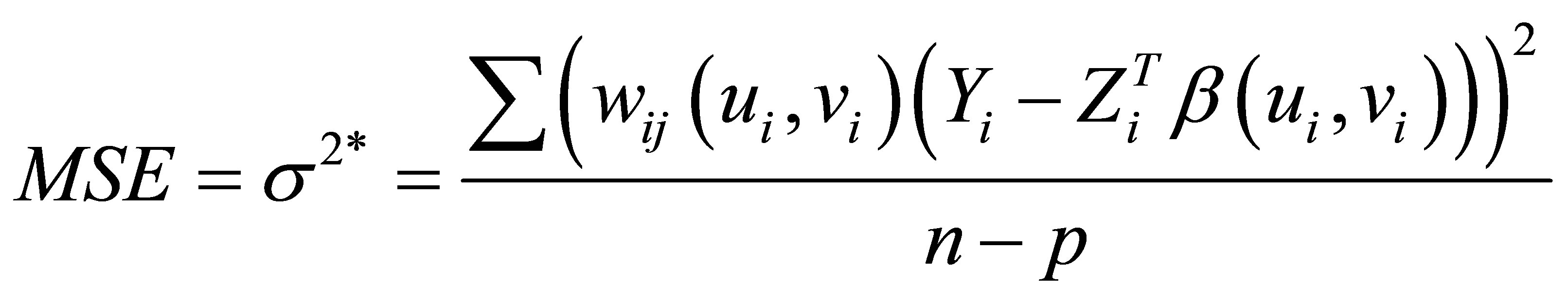obtained

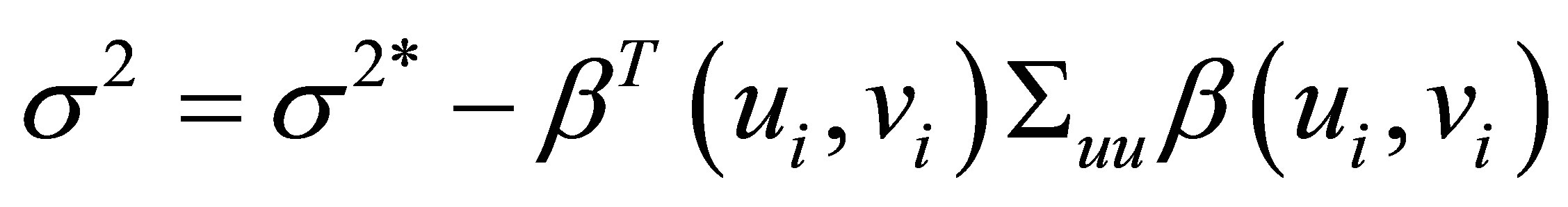
so

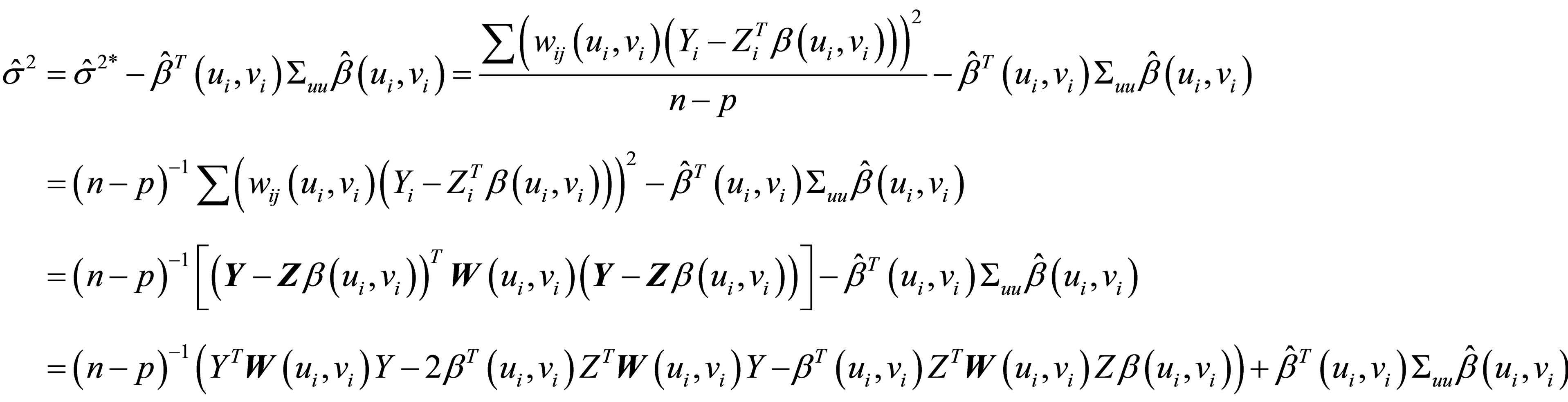(3.4)

If Equation (3.4) derived to and the result equated to zero then obtain parameter estimators

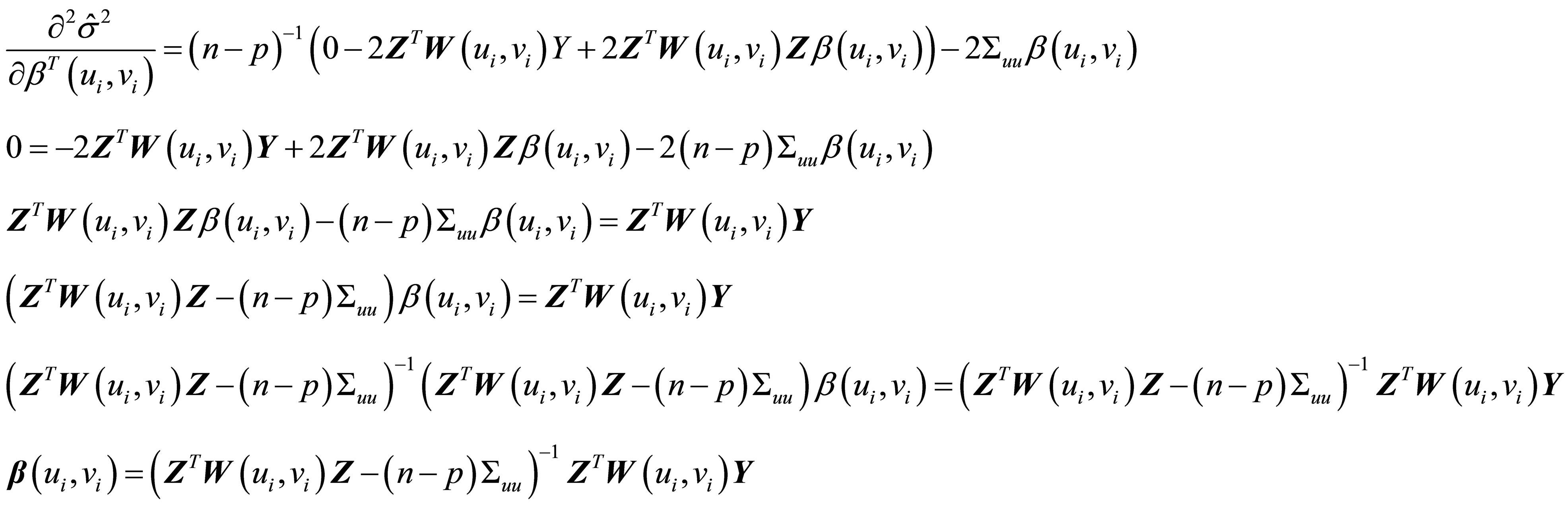
The parameter estimation of geographically weighted regression models with the measurement error for each location is

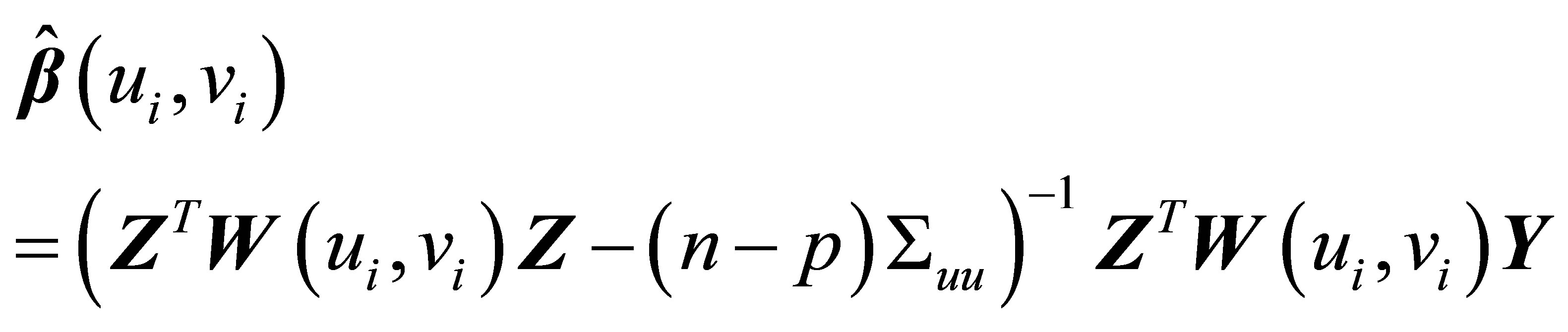(3.5)

4. Statistical Properties

After obtaining the estimators 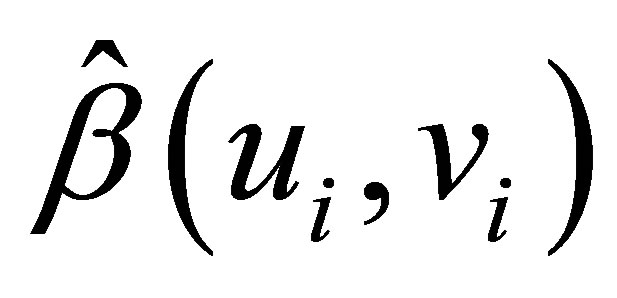it will look for the properties of the estimator in Equation (3.5). From Equation (2.1), weighted regression with measurement errors obtained:

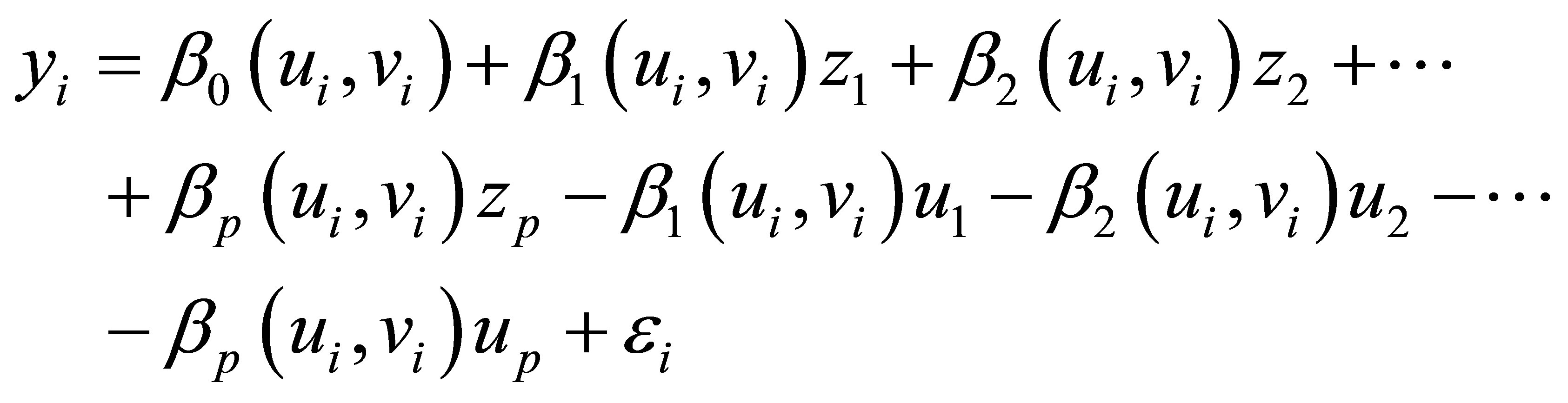
which can also be written as

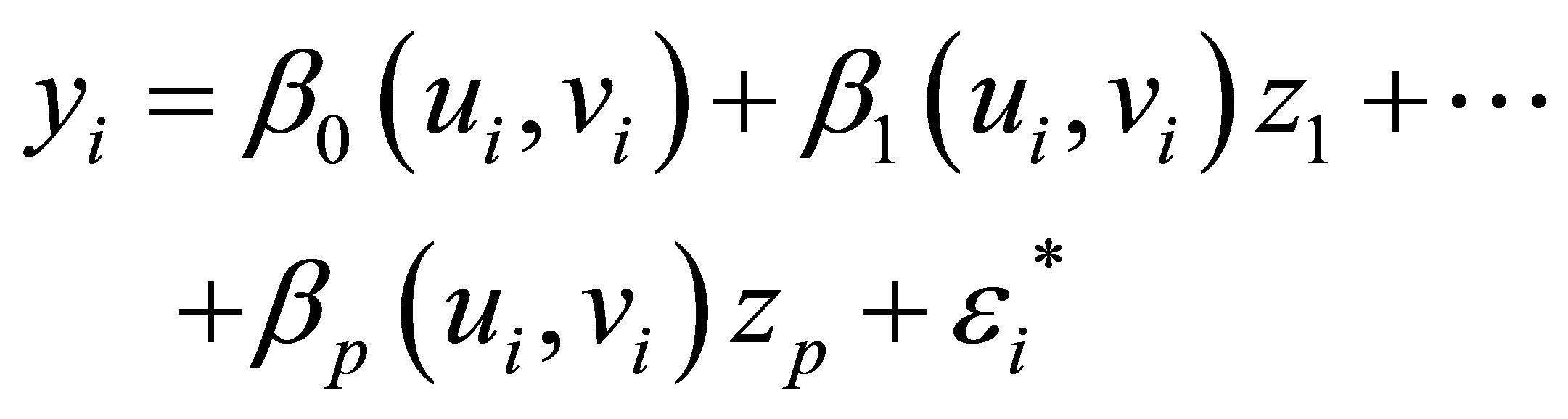(4.1)

where

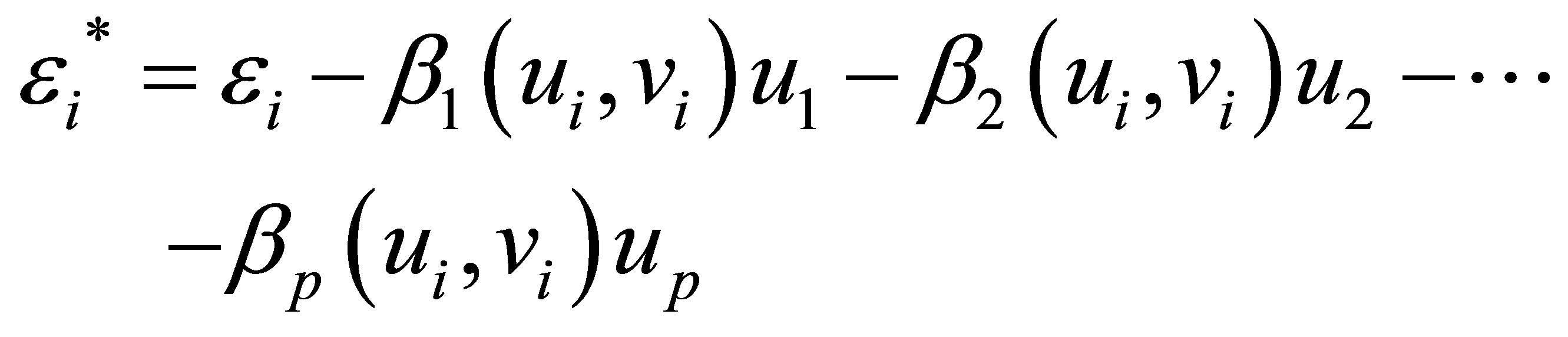
In matrix notation, the regression Equation (4.1) is

(4.2)

Estimating the parameters obtained from the weighted

From the above Equation we can see that

so that the estimator is a biased estimator for.

[13] found that the instrumental variable method provided unbiased estimates in linear models. To prove the unbiasedness, we use a linear model with covariates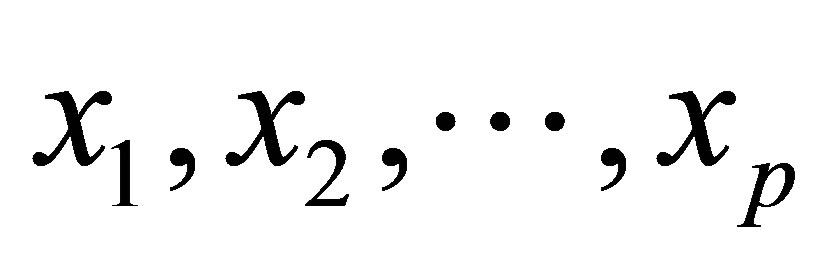. Suppose 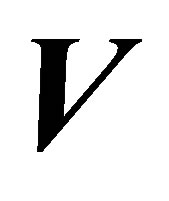is the matrix containing the instrumental variables and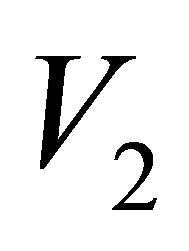, i.e.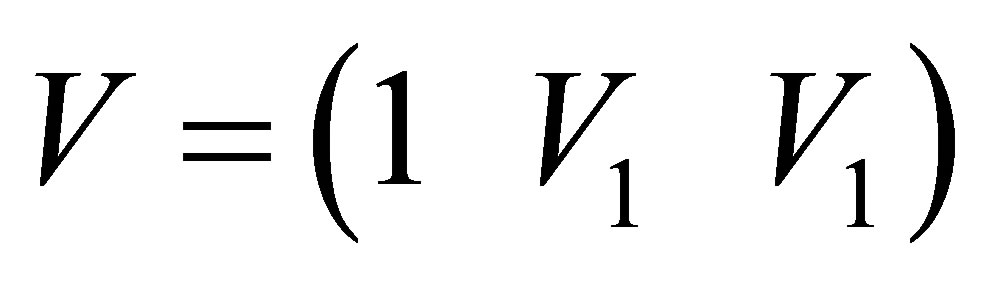, where “1” indicates the vector of ones which is needed for the intercept. According to the definition of instrumental variables [2], V and 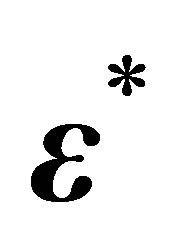are independent. Therefore,

To obtain the parameter estimates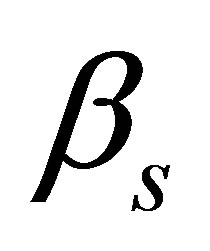, we create a “quasi” normal Equation by pre-multiplying both sides of Equation (4.2) with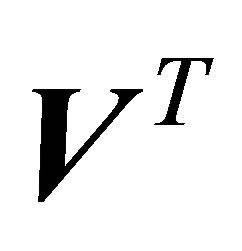, and hence, we obtain

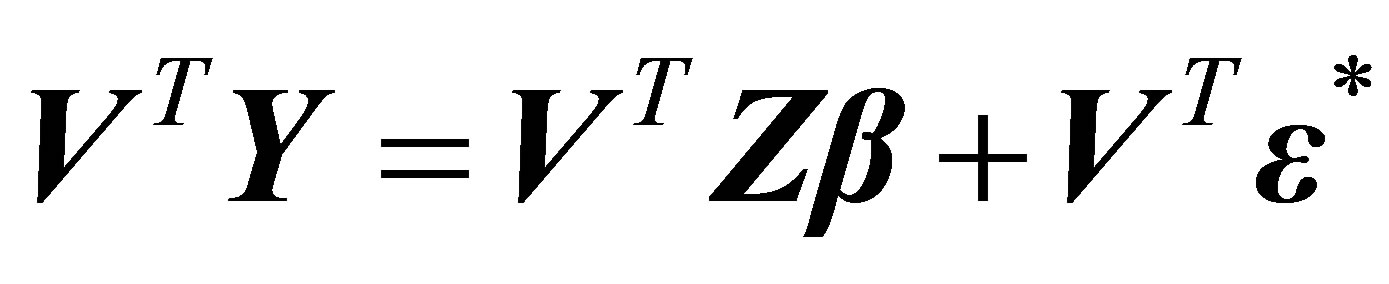(4.3)

Since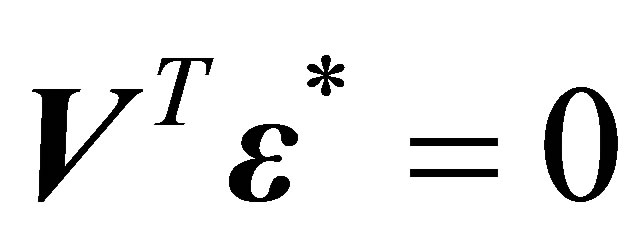, Equation (4.3) above becomes

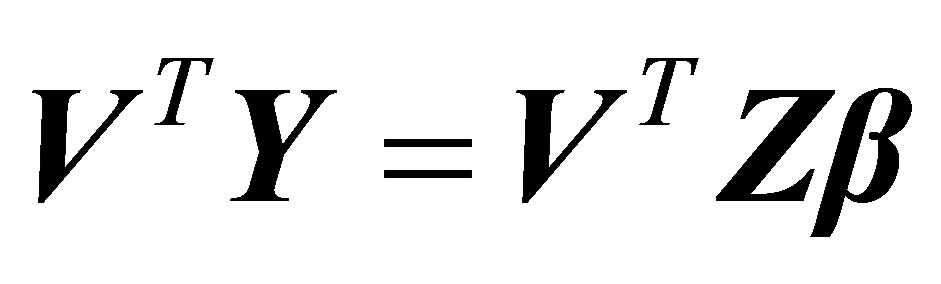
Therefore, the unbiased estimates 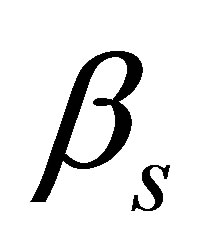obtained by the instrumental variable technique are

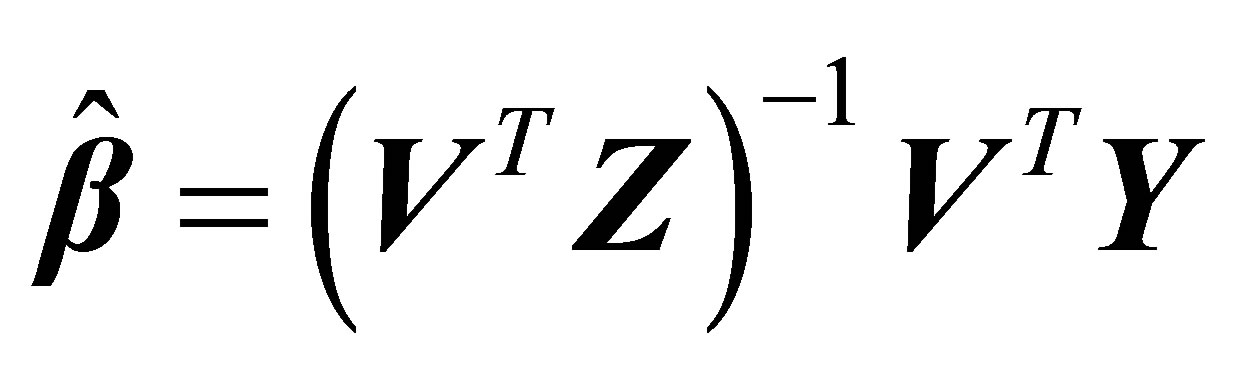
Despite the fact that it is sometimes difficult to find variables serving purely as instrumental variables [14], this technique is a good option to overcome the problems of measurement error [13]. In addition, [15] proposed an instrumental variable technique as a method to estimate the reliability coefficient of covariates that are difficult to measure.

To prove whether 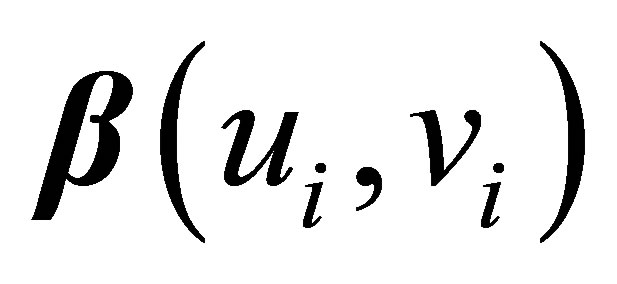is an efficient estimator is

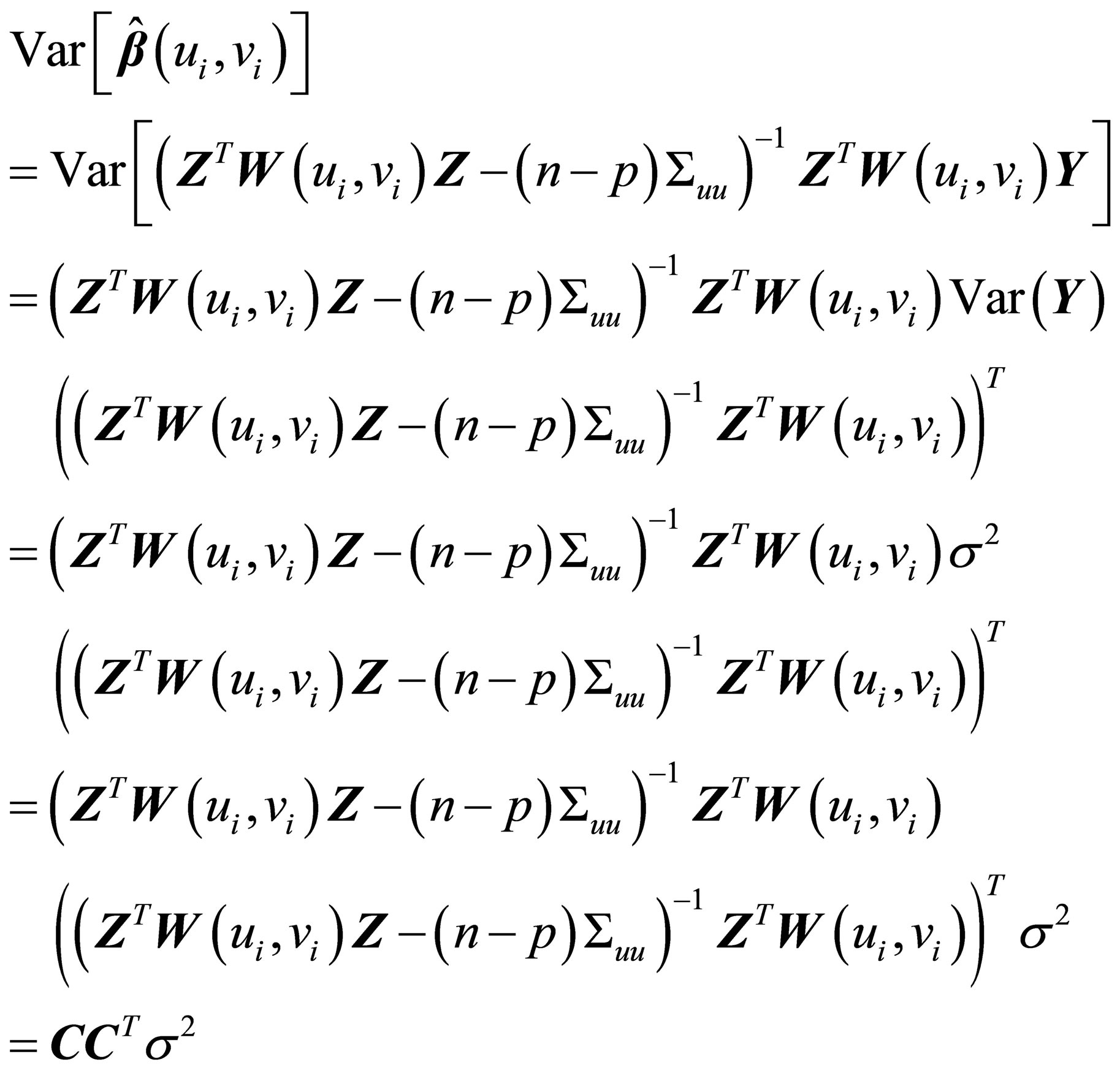
with

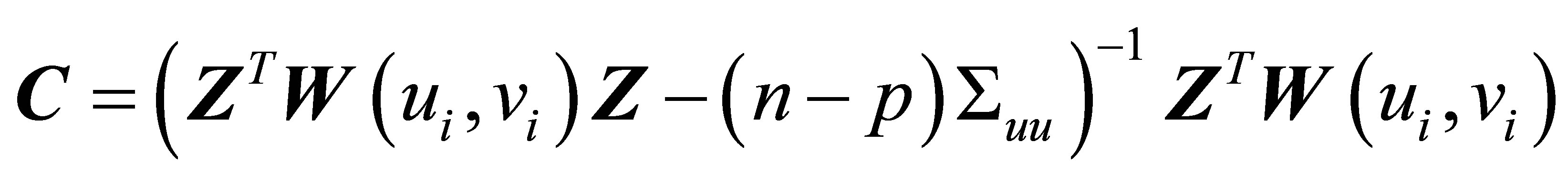
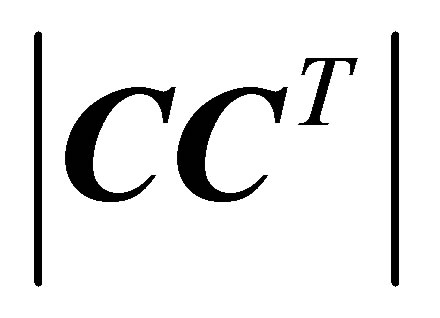should be as small as possible so that efficient estimator.

5. Summary

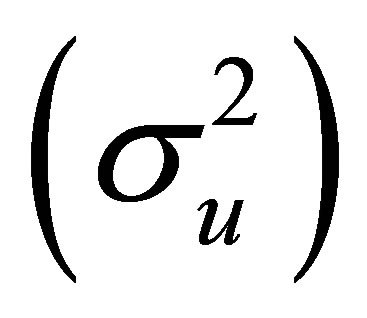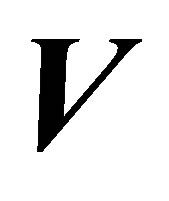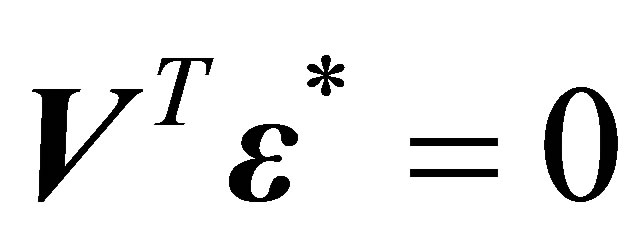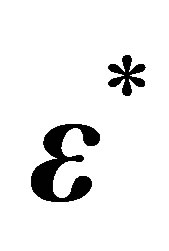In this paper, we assume that the variance of the measurement error is known. Assumptions used in this model are the errors normally distributed with that expected value is zero and the variance is constant. Geographically weighted regression models with the measurement error use the instrumental variable method. gives the unbiased estimation in the linear model, with terms. and are independent. The properties of estimators of geographically weighted regression models with the measurement error are an efficient estimator if 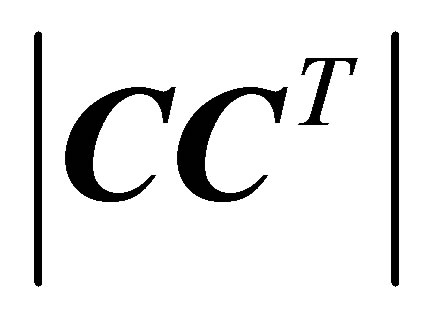should be as small as possible.

REFERENCES