ABSTRACT

One of the important fields in statistics is testing hypothesis of correlation coefficient. The extension of the idea of testing correlation to fuzzy hypothesis is of great interesting. In this study, we examined the use of fuzzy hypothesis testing approach for the Sequential Probability Ratio Test (SPRT) of correlation coefficient. Use of fuzzy hypothesis testing for correlation coefficient with SPRT is illustrated by an example.

1. Introduction

Correlation coefficient (ρ) is found to have applications in some area such as medicine, genetics, psychology, numerical taxonomy and quality control [1]. In these areas, the data is obtained sequentially. Thus it is advantageous to use sequential tests.

Wald [2] proposed SPRT which is designed to decide between two simple hypotheses. SPRT require substantially fewer observations than fixed sample size test.

The SPRT for the correlation coefficient has been investigated by Choi [3], Kowalski [1] and Pradhan and Sathe [4]. Choi [3] developed a SPRT which is essentially a test for the Cauchy parameter. Kowalski [1] derived a SPRT under the bivariate normal distribution.

Pradhan and Sathe [4] proposed an unbiased estimator of correlation coefficient. This estimator suggested a SPRT for 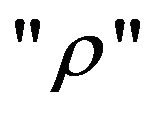which reduces to an SPRT for the Bernoulli parameter, which is a simple function of, but two pairs of observations need each step. Pradhan and Sathe’s SPRT is more efficient than Kowalski’s and Choi’s tests [4].

There are several components for making decisions in traditional statistics such as crispness of data, random variables, hypothesis testing, decision rules and so on. There have been several attempts to analyze above situations with fuzzy set theory developed by Zadeh [5]. One of them is fuzzy hypothesis testing procedure. In fuzzy hypothesis testing the sample data and hypotheses are either crisp or fuzzy. In this study we focus on fuzzy hypothesis with crisp observations.

Several authors have proposed SPRT for fuzzy case. Neyman Pearson lemma for fuzzy hypothesis testing was given by Taheri and Behboodian [6]. Torabi and Behboodian [7] gave the SPRT for fuzzy hypothesis testing with fuzzy observations. Talukdar and Baruah [8] have fuzzified SPRT. Torabi and Mirhosseini [9] introduced a SPRT for fuzzy hypothesis testing. They developed fuzzy SPRT for testing the mean of Normal distribution with known variance and the parameter of Bernoulli distribution 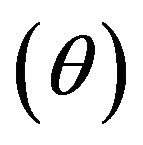Akbari [10] proposed a new approach for SPRT of fuzzy hypothesis under density probability function. Testing hypothesis concerning correlation coefficient with fuzzy data was investigated by Leu et al. [11].

In this study, we apply SPRT to test fuzzy hypothesis for the correlation coefficient of a bivariate normal distribution. Then this method is demonstrated by an example.

This paper is organized as follows: in Section 2, SPRT for the correlation coefficient [4] is given. In Section 3, some of the basic concepts of fuzzy hypothesis testing are defined and reviewed. In Section 4, Torabi and Mirhosseini’s SPRT approach for Bernoulli parameter is given [9]. In addition we apply this fuzzy SPRT to test fuzzy hypothesis for the correlation coefficient. Then an example and conclusion are presented in Sections 5 and 6.

2. Sequential Test for the Correlation Coefficient

Let the independent random variable 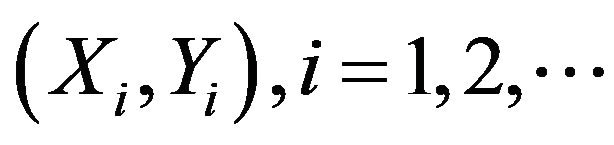be from bivariate normal distribution. Than the correlation coefficient is given as

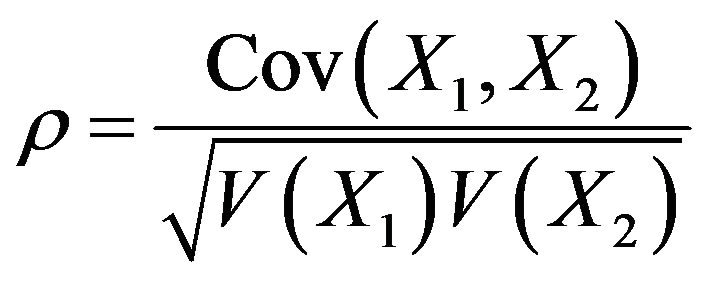(1)

Let the hypothesis to be tested be

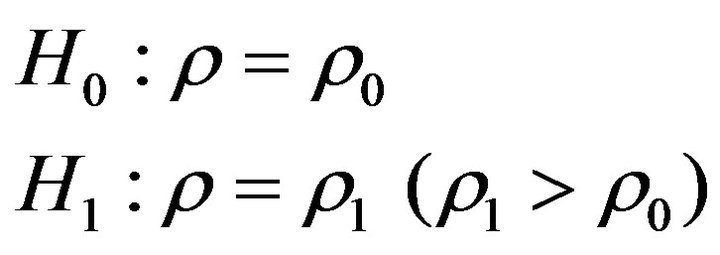(2)

where 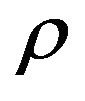is a positive or negative constant

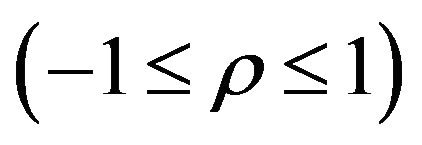. Pradhan and Sathe [4] gave Theorem 1 which establishes a basic relationship between correlation coefficient 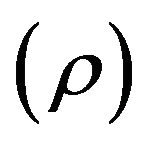and the Bernoulli parameter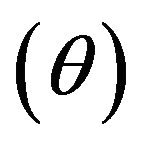

Theorem 1: Let the independent random variables 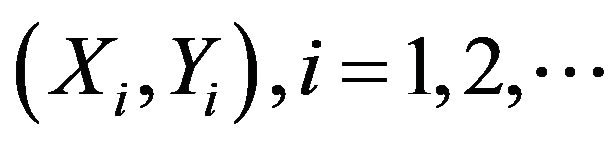be from bivariate Normal distribution

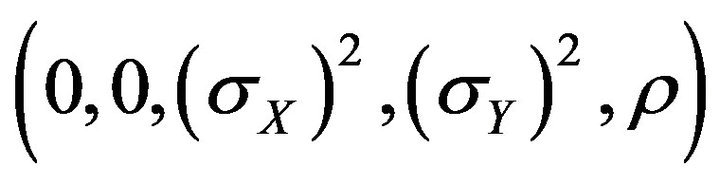. Then,

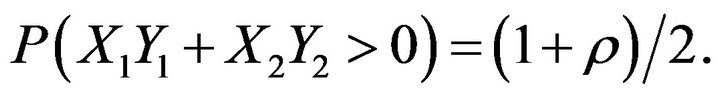(3)

In the sequential testing procedure, it is taken two pairs of observations at each step. At the ith step it is defined as,

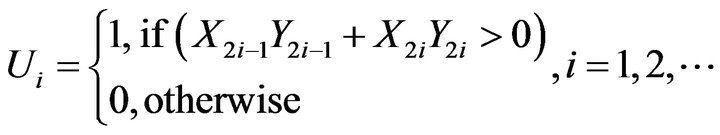(4)

Then 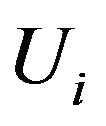follows Bernoulli distribution with

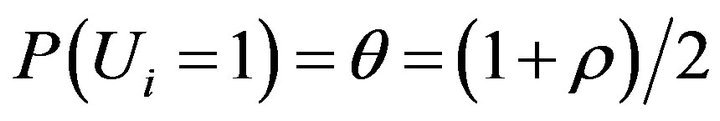. (5)

Hence hypotheses for the correlation coefficient (2) can be written as,

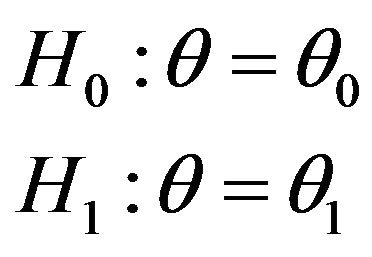(6)

and SPRT for the Bernoulli parameter can be applied [2].

For testing 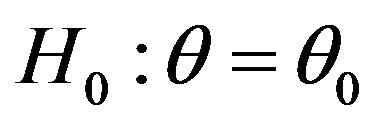versus 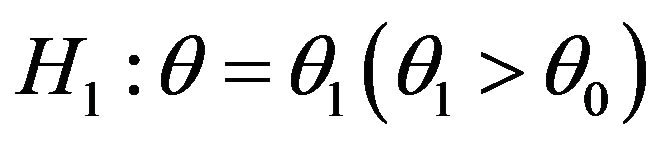SPRT is defined as follows:

Let 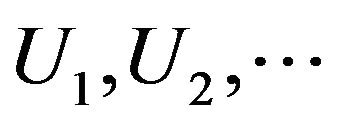be a sequence i.i.d. rv’s from Bernouilli distribution Ber 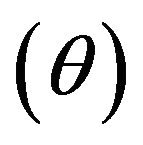where,

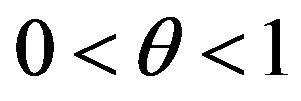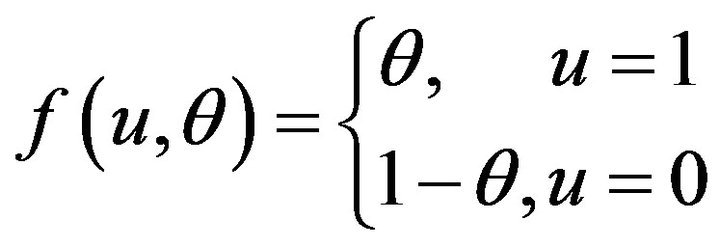(7)

then the likelihood ratio is,

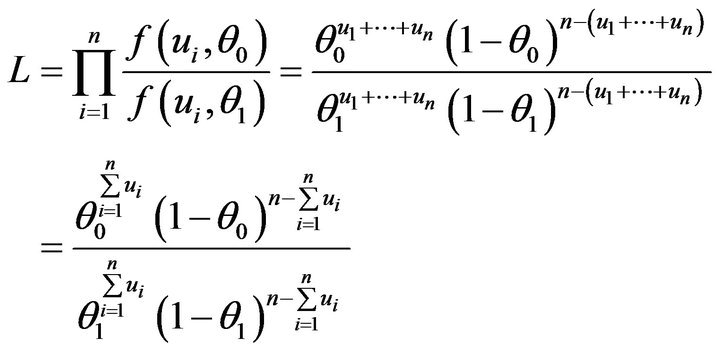(8)

By taking logarithm and simplifying, Equation (8) can be written as,

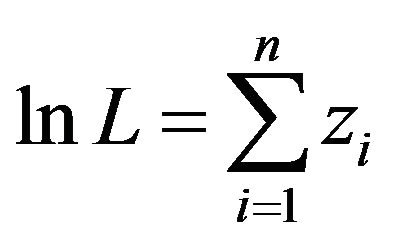(9)

where is taken as following

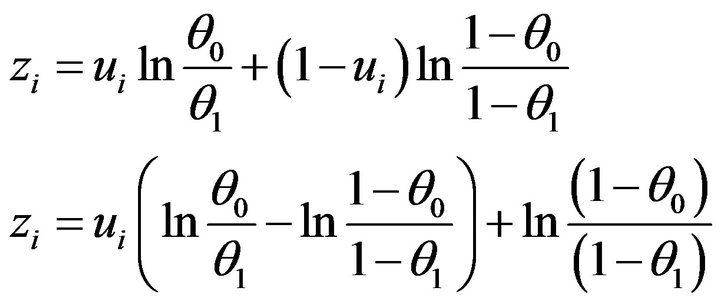(10)

Hence

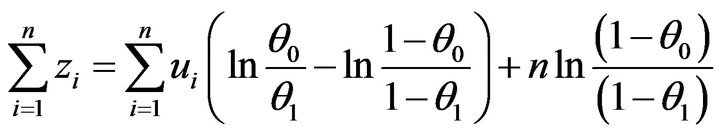. (11)

After each observation is computed the 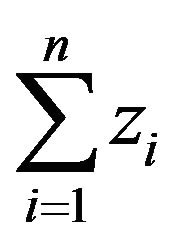and compared with 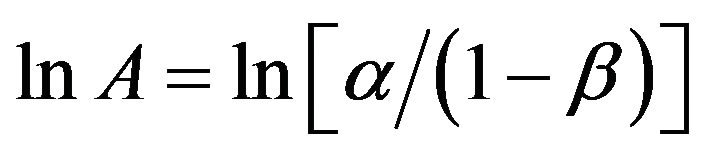and

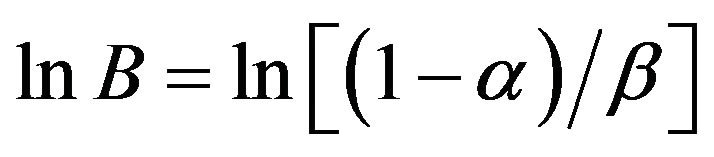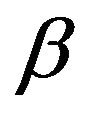, where is the type I and is the type II error probability. Then one of the following decisions is reached 1) If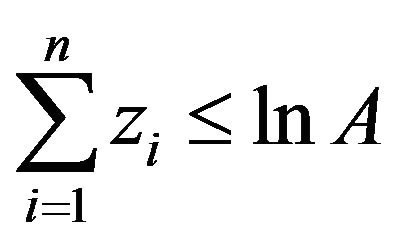, reject 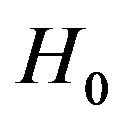and stop sampling.

2) If 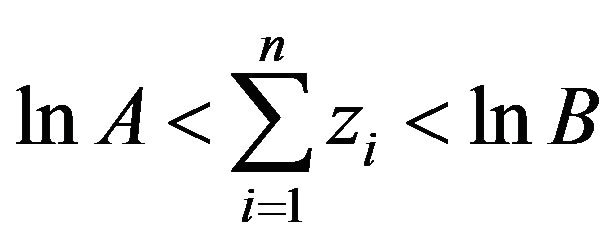continue sampling.

3) If 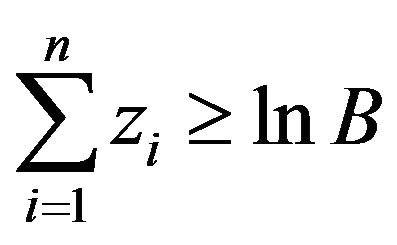accept 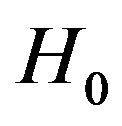and stop sampling.

Let 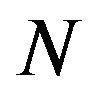be the random variable denoting the sample size of the SPRT. The SPRT with and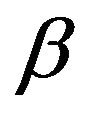, expected sample size when the 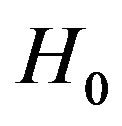is true,

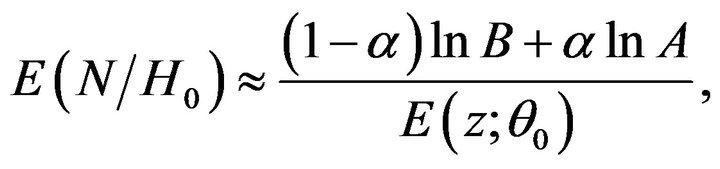(12)

otherwise, when 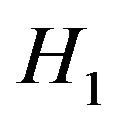is true,

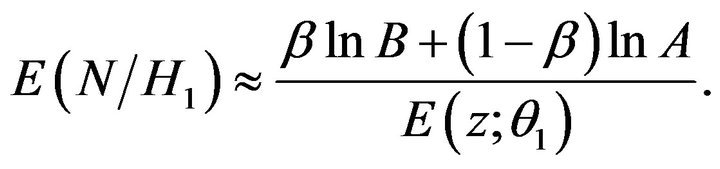(13)

where 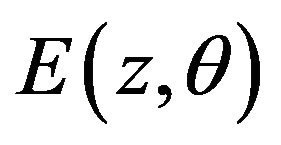is defined as from Equation (10) ()

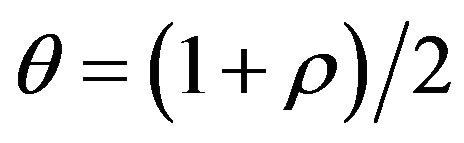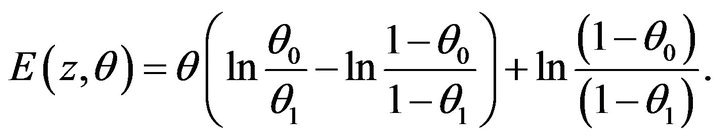(14)

Pradhan-Sathe’s [4] SPRT need two pairs of observations each step. Therefore, the expected sample size of this SPRT is given by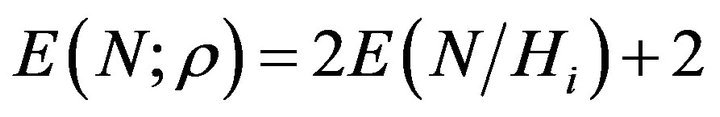, for.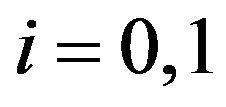

3. Fuzzy Hypothesis Testing

We may face a fuzzy hypothesis in practice in many areas [6,9,12]. Hence, in this section we briefly introduce some definitions about fuzzy hypothesis testing (FHT).

Preliminaries

Some preliminaries are given below for testing fuzzy hypotheses.

Definition 3.1 Any hypothesis of the form “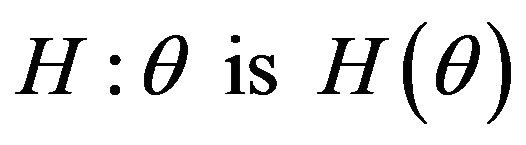” is called fuzzy hypothesis (FH), where “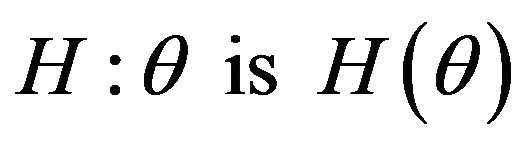” implies that is in a fuzzy set of (the parameter space) with membership function 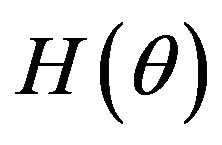i.e. a function from to.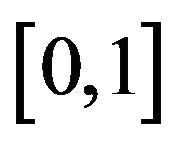

Note that the ordinary hypothesis 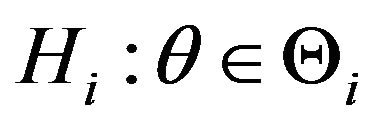is a fuzzy hypothesis with membership function 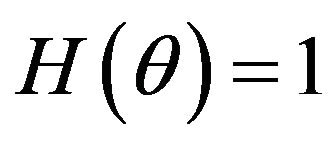at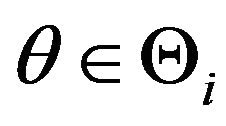, and zero otherwise, i.e., the indicator function of the crisp set 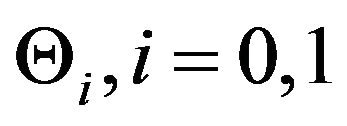[6,7]

Definition 3.2 In FHT with crisp data, the main problem is testing

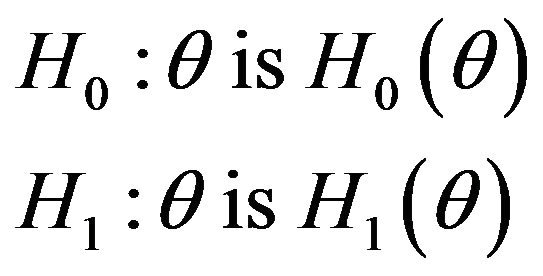(15)

according to a random sample 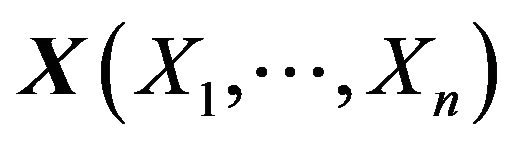from a parametric population with the probability density function (PDF)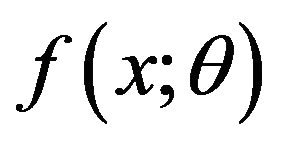. It follows that the PDF of the random sample X is [12]

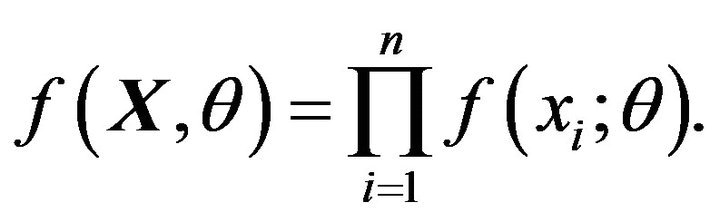(16)

Definition 3.3 The pseudo-membership function of 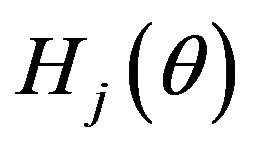is defined by

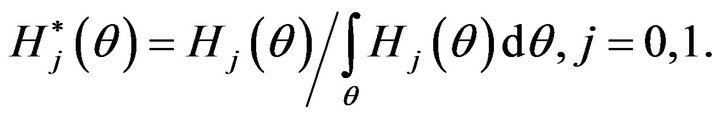(17)

Substitute ∫ by 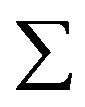in discrete cases; i.e. in the case that has just uncountable values [9].

Definition 3.4 Let X be a random variable with PDF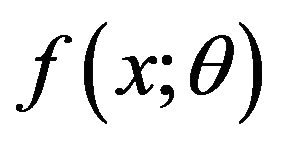. Under the hypothesis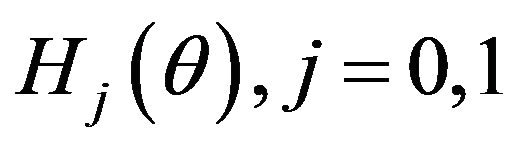, the weighted probability density function (WPDF) of X is defined by

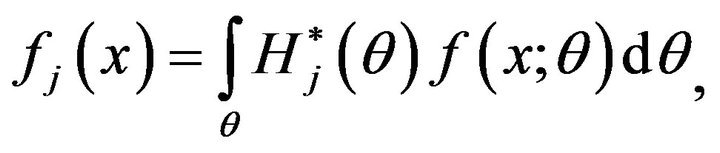(18)

i.e., the expected value of 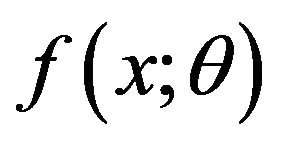over

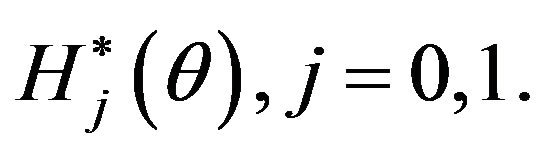If X is a random sample from PDF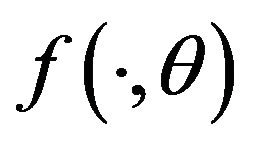, then the joint WPDF of X is defined by

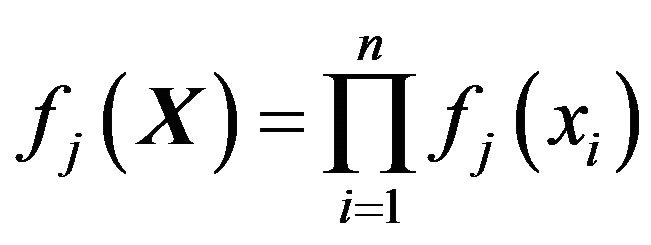. (19)

Then the weighted likelihood ration is defined as [6]

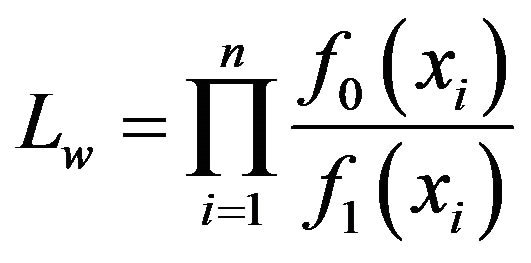. (20)

4. Fuzzy Hypothesis Testing for the Sequential Probability Ratio Test of Correlation Coefficient

It is known that correlation coefficient is related to the Bernoulli parameter 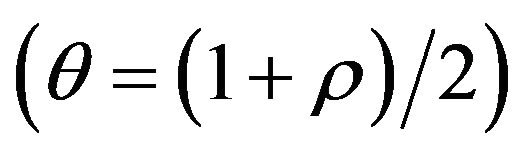[4]. In the sense of this information which is given in Section 1 with Theorem 1, hypothesis testing for correlation coefficient with Equation (2) can be written as

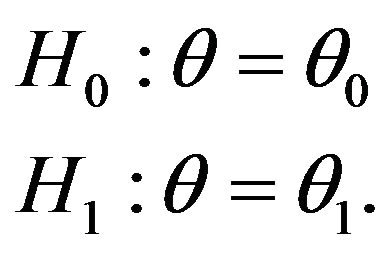(21)

Therefore, Torabi and Mirhosseini’s [9] fuzzy SPRT for the Bernoulli parameter can be applied. For testing (21) fuzzy SPRT is defined as follows:

Let 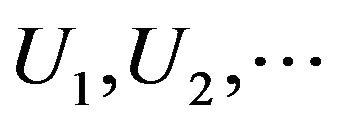be a sequence of i.i.d. r.v.’s from Bernoulli distribution,

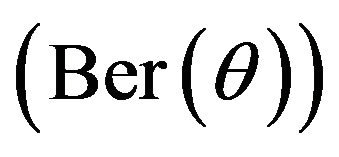. (22)

We want to test

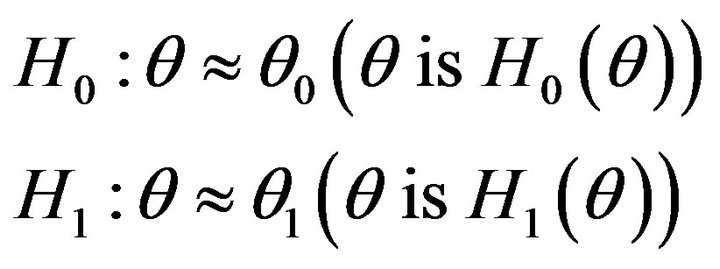(23)

with the membership functions [9]

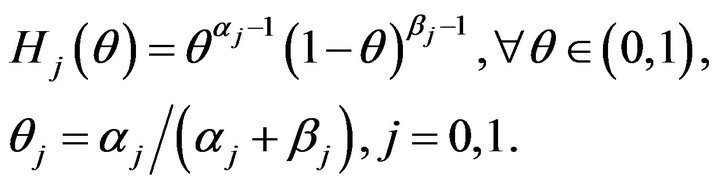(24)

The pseudo-membership function of 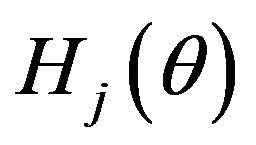is defined from Definition 3.3,

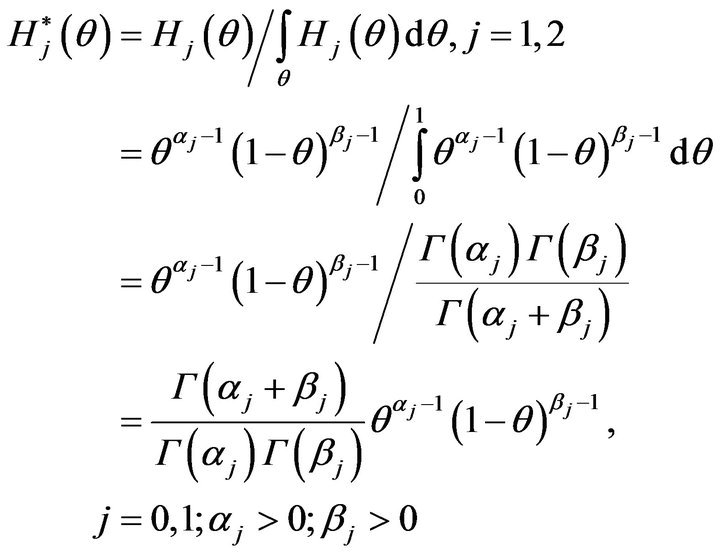(25)

Hence 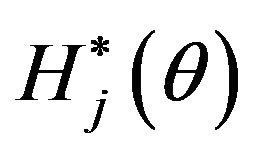is Beta distribution. The weighted probability density function of is defined by (Definition 3.4)

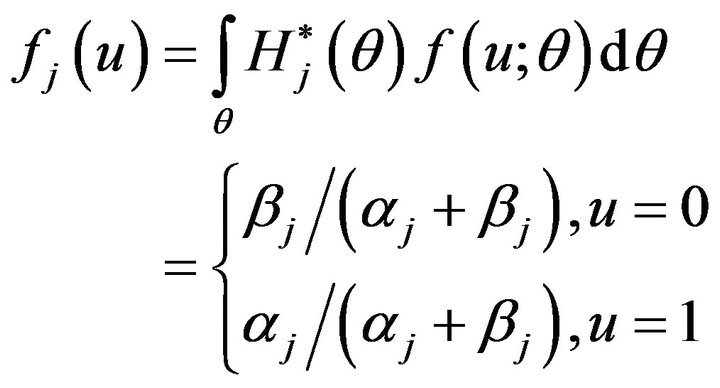(26)

Hence the FHT (Equations (23)) is equivalent to

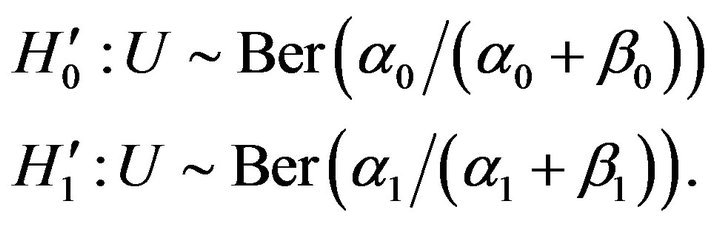(27)

Thus, test statistics for the sequential FHT weighted probability density function can be defined as

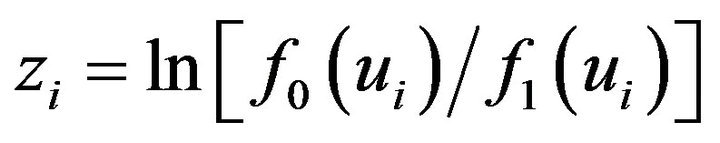. (28)

Then SPRT test statistic defined in Section 2 can be obtained as

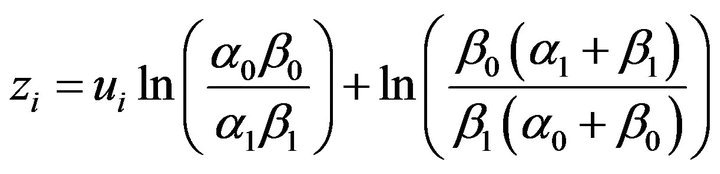. (29)

Hence,

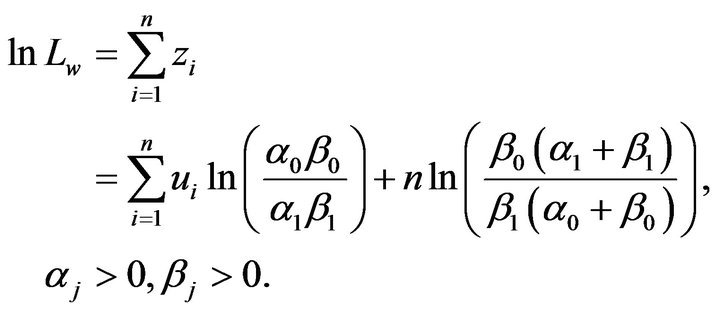(30)

Expected value of and 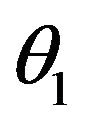is defined as

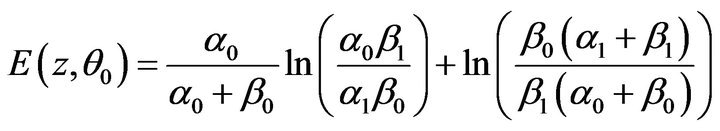(31)

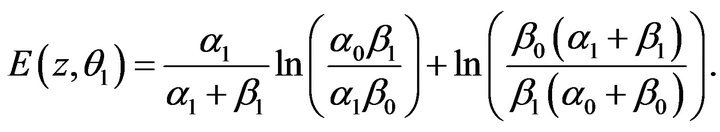(32)

Let N be the random variable denoting the sample size of the fuzzy SPRT. The fuzzy SPRT with and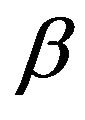, the expected sample size when 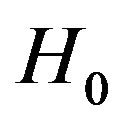is true,

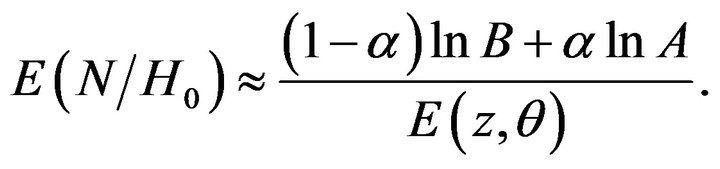(33)

Otherwise, when 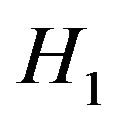is true,

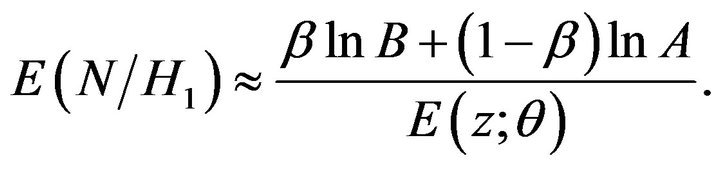(34)

As it is mention in Section 2, SPRT’s observation equation which is 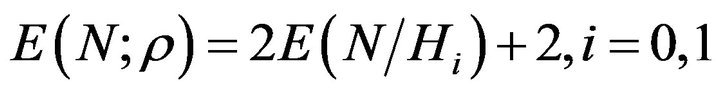is still valid for the FHT of correlation coefficient.

Therefore in this study we showed that fuzzy hypothesis testing for correlation coefficient can be applied using Torabi and Mirhosseini’s [9] SPRT.

5. Example

In this section we present an example to clarify the method so far. Let 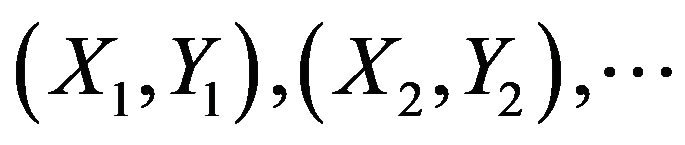be a sequence from iid r.v.’s from Bivariate Normal distribution. We want to test

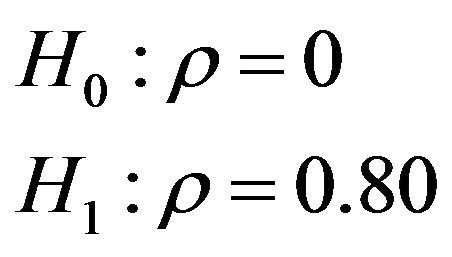(35)

It is possible to write this hypothesis as follows according to the information given with Theorem 1 in Section 2

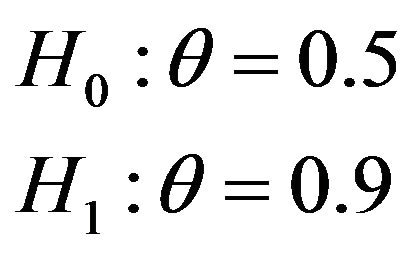(36)

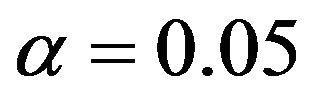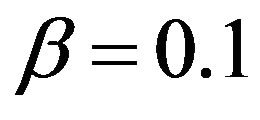Let and then we calculate

and. It is known that Prathan-Sathe’s [4] SPRT needs two pair of observations each step. Therefore the expected sample size of this SPRT is given by

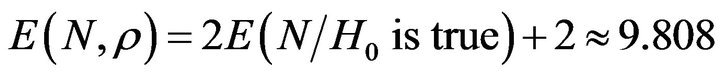. These results are obtained by applying classical hypothesis testing procedure which is assumed that both the underlying hypotheses are crisp. However, we want to test if the correlation coefficient is nearly zero or nearly 0.8. Because fuzzy approaches are extremely popular in real life situations and it ensures to obtain closer values to real results [6,8,11]. Hence crisp hypothesis turns into fuzzy hypothesis given below

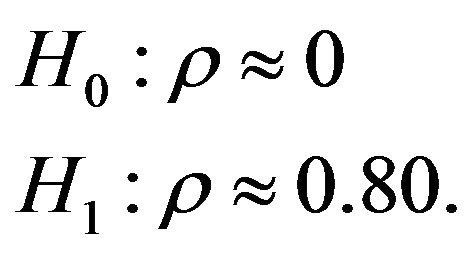(37)

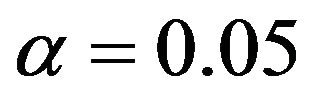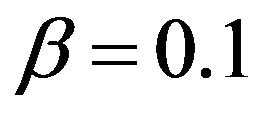It is known that and. Then we write this hypothesis with Equation 38 by combining the information given in Section 2 and Section 3 as

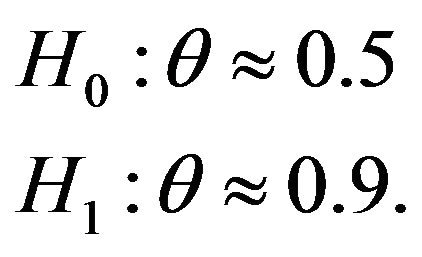(38)

In addition, we determined,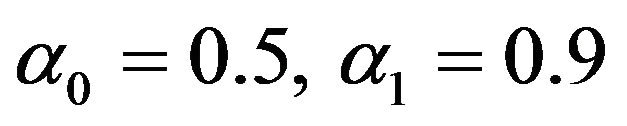

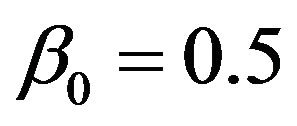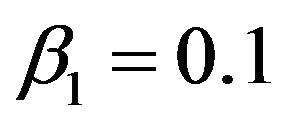,. Then, membership functions can also be defined as

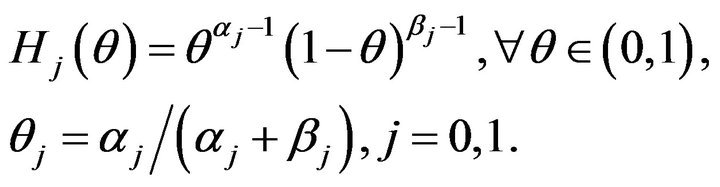(39)

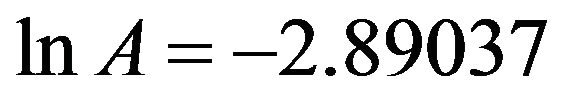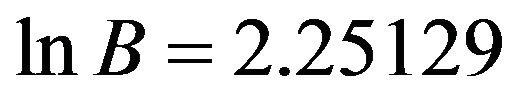Afterwards we calculate and

, and

Hence we obtain

and

.

6. Conclusion

In this study, the use of SPRT to test fuzzy hypothesis concerning the correlation coefficient for the bivariate normal distribution is examined. It is known that one can develop SPRT for simple fuzzy hypothesis for correlation coefficient. However, in real world, we may confront with fuzzy hypothesis. According to recent studies, the methods taking into account the statistical hypothesis with fuzzy approaches can be so worthwhile. Thus, in this study, we showed that fuzzy hypothesis testing procedure can be used for SPRT of correlation coefficient.

REFERENCES