Open Journal of Statistics
Vol. 2 No. 1 (2012) , Article ID: 17141 , 9 pages DOI:10.4236/ojs.2012.21005
A New Method of Construction of Robust Second Order Rotatable Designs Using Balanced Incomplete Block Designs
Department of Statistics, Acharya Nagarjuna University, Guntur, India
Email: victorsugnanam@yahoo.co.in
Received December 8, 2011; revised December 30, 2011; accepted January 12, 2012
Keywords: Response Surface Designs; Rotatability; Second Order Rotatable Designs (SORD); Robust SORD; Robustness; Balanced Incomplete Block Designs
ABSTRACT
Das [1,2] studied robust second order rotatable designs (RSORD) and constructed second order rotatable designs with correlated errors (SORDWCE) under the auto correlated structure using central composite design. In this paper, a new method of construction of RSORD using balanced incomplete block designs (BIBD) is suggested. In this method the number of design points required is in some cases less than the number required in Das [1,2] method of construction of robust rotatable central composite designs (RRCCD). We may point out here that this RSORD using BIBD has 113 design points for 7-factors where as the corresponding RRCCD obtained by Rajyalakshmi and Victorbabu [3] needs 157 design points. Thus the new method leads to a 7-factor RSORD in less number of design points than the corresponding RRCCD. Here we also obtained the variance of the estimated response for the factors 3 ≤ v ≤ 8.
1. Introduction
In response surface methodology, rotatability is a natural and highly desirable property. This was introduced and developed by Box and Hunter [4], assuming the errors to be uncorrelated and homoscedastic. Das and Narasimham [5], constructed second order rotatable designs (SORD) through balanced incomplete block designs (BIBD). Panda and Das [6] studied first order rotatable designs with correlated errors. Further, Rajyalakshmi and Victorbabu [3] extended the work of Das [1,2] and constructed RRCCD for 3 ≤ v ≤ 17.
In order to study the nature of robust rotatable designs, rotatability conditions for second order regression designs have been derived, assuming the errors to be correlated. These conditions have been further studied under different variance covariance structures of errors. Here we derive conditions for rotatability for a general correlated errors structure and specialize then to the autocorrelated structure.
In this paper, a new method of construction of RSORD using BIBD is suggested and also obtained the variance of the estimated response for factors 3 ≤v ≤ 8.
2. Conditions of SORDWCE
Assuming that the response surface is of second order, we adopt the model:
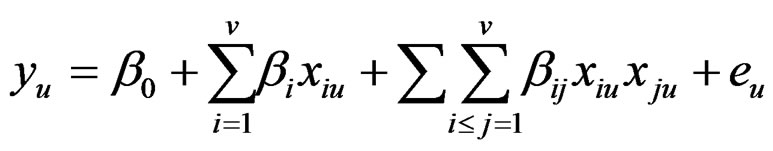 (1)
(1)
where Y is the vector of recorded observations on the study variable y, β’s are the vector of regression coefficients, eu are random errors with correlated errors.
2.1. Conditions of Rotatability
The estimated response at x is given by
 (2)
(2)
The variance of estimated response at  is given by
is given by
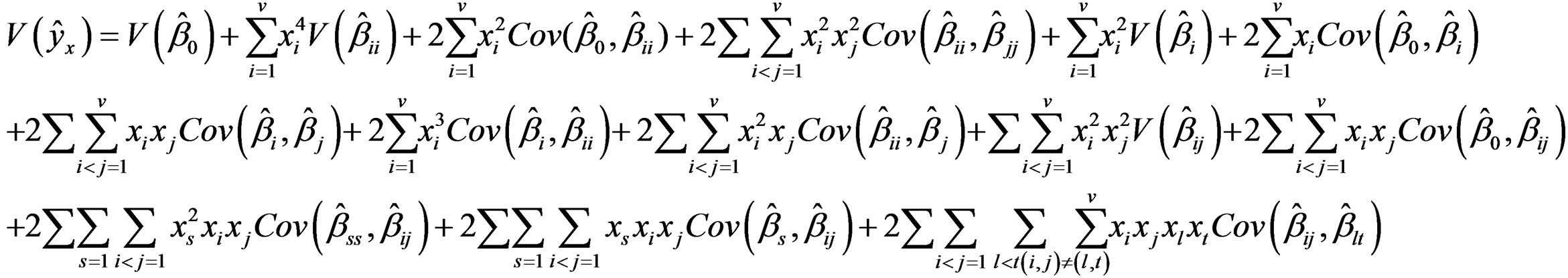 (3)
(3)

(4)
The variance function in (3) will be a function of 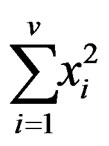
for rotatability for all x if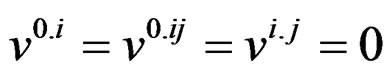 ; 1 ≤ i ≠ j ≤ v;
; 1 ≤ i ≠ j ≤ v;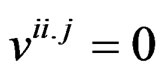 ; 1≤ i, j ≤ v;
; 1≤ i, j ≤ v;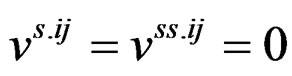 ; 1 ≤ s, i < j ≤ v;
; 1 ≤ s, i < j ≤ v;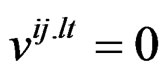 ; 1 ≤ i, l < j, t ≤ v, (i, j) ≠ (l, t);
; 1 ≤ i, l < j, t ≤ v, (i, j) ≠ (l, t);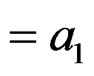
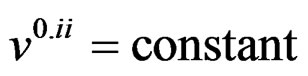 , say; 1≤ i ≤ v;
, say; 1≤ i ≤ v;  = constant = e, say; 1≤ i ≤ v;
= constant = e, say; 1≤ i ≤ v; , say; 1 ≤ i ≠ j ≤ v;
, say; 1 ≤ i ≠ j ≤ v; 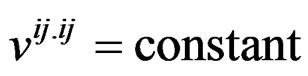
 , say; 1 ≤ i < j ≤ v; and
, say; 1 ≤ i < j ≤ v; and ; 1 ≤ i
; 1 ≤ i
≤ v.
Below are given equivalent conditions for rotatability in second order regression designs with correlated errors model (1) in terms of the elements of the moment matrix:
(I): (i)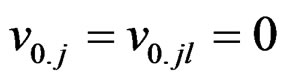 ; 1 ≤ j < l ≤ v
; 1 ≤ j < l ≤ v
(ii)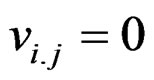 ; 1 ≤ i ≠ j ≤ v
; 1 ≤ i ≠ j ≤ v
(iii) (1)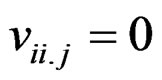 ; 1 ≤ i, j ≤ v
; 1 ≤ i, j ≤ v
(2)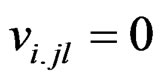 ; 1 ≤ i, j < l ≤ v
; 1 ≤ i, j < l ≤ v
(3)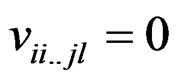 ; 1 ≤ i, j < l ≤ v
; 1 ≤ i, j < l ≤ v
(4)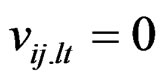 ; 1 ≤ i, l< j, t ≤ v, (i, j) ≠ (l, t)
; 1 ≤ i, l< j, t ≤ v, (i, j) ≠ (l, t)
(II): (i) , say; 1 ≤ j ≤ v
, say; 1 ≤ j ≤ v
(ii) , say; 1 ≤ i ≤ v
, say; 1 ≤ i ≤ v
(iii)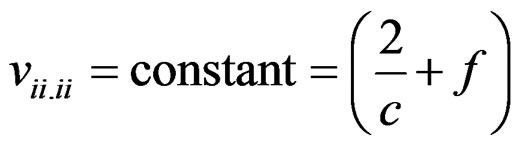 , say; 1 ≤ i ≤ v
, say; 1 ≤ i ≤ v
(III): (i) ; 1 ≤ i ≠ j ≤v
; 1 ≤ i ≠ j ≤v
(ii)  ; 1 ≤ i < j ≤v
; 1 ≤ i < j ≤v
(IV):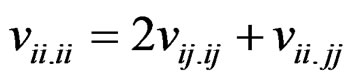 ; 1 ≤ i < j ≤ v (5)
; 1 ≤ i < j ≤ v (5)
2.2. Variance Function of SORDWCE
The estimated response at x is given by
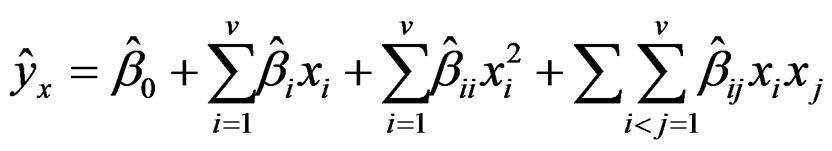 (6)
(6)
The variance function of a SORDWCE is given by
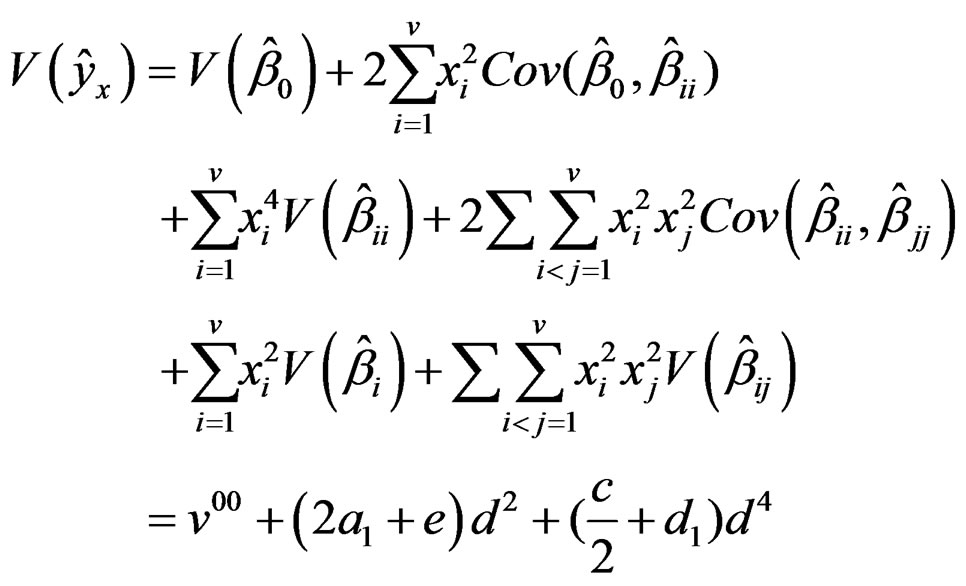 (7)
(7)

Note: When the errors are homoscedastic, (5) and (7) reduce respectively to the usual second order rotatability conditions, non-singularity condition and variance function.
2.3. Conditions for Exact Rotatability
Following (4), necessary and sufficient conditions for second order rotatability under auto-correlated structure, it is simplifies to

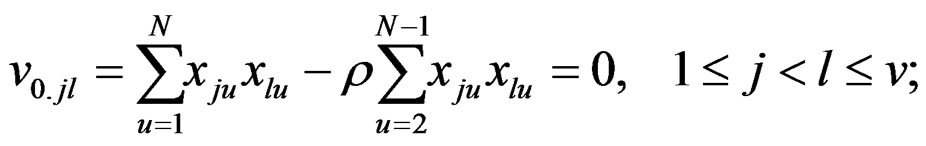
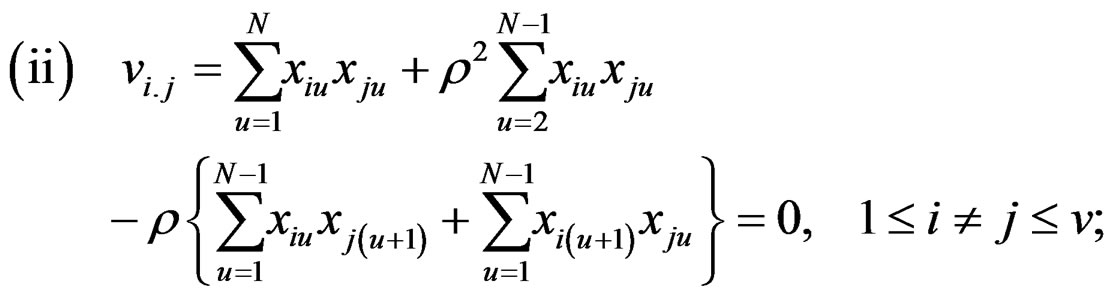

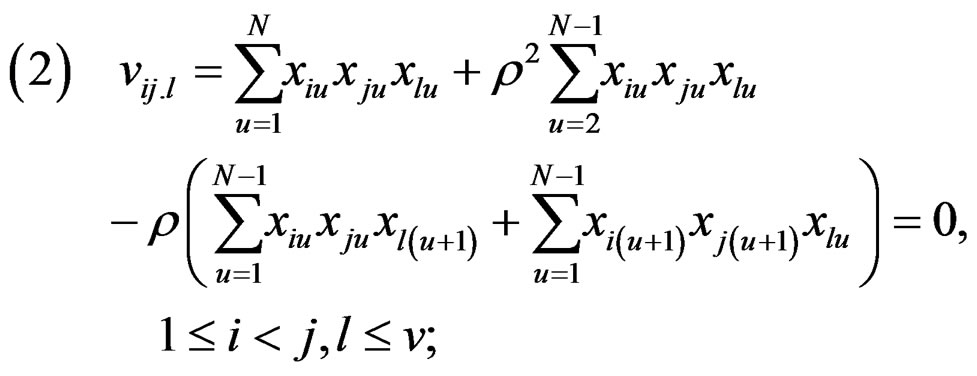
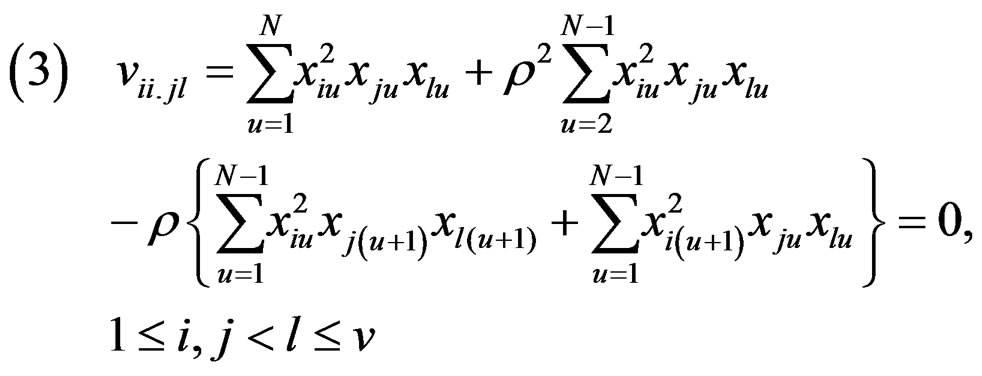

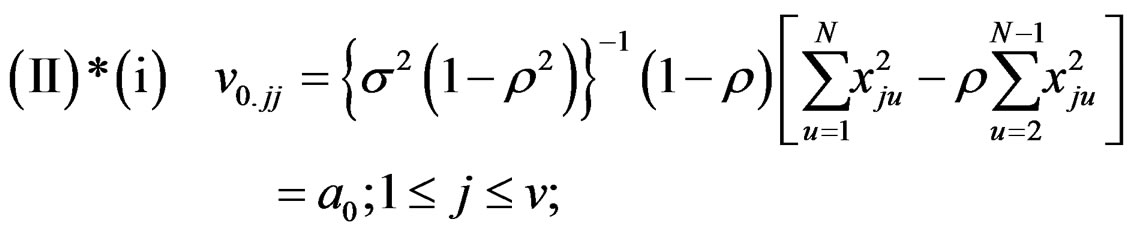

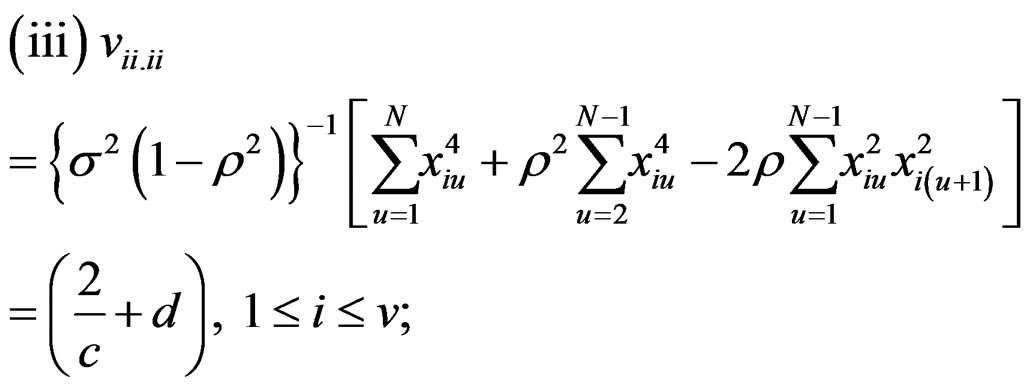
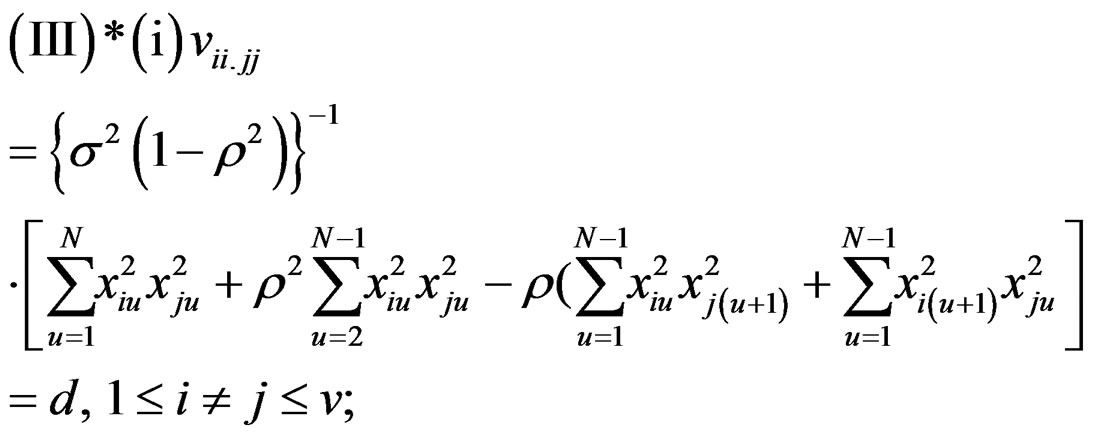
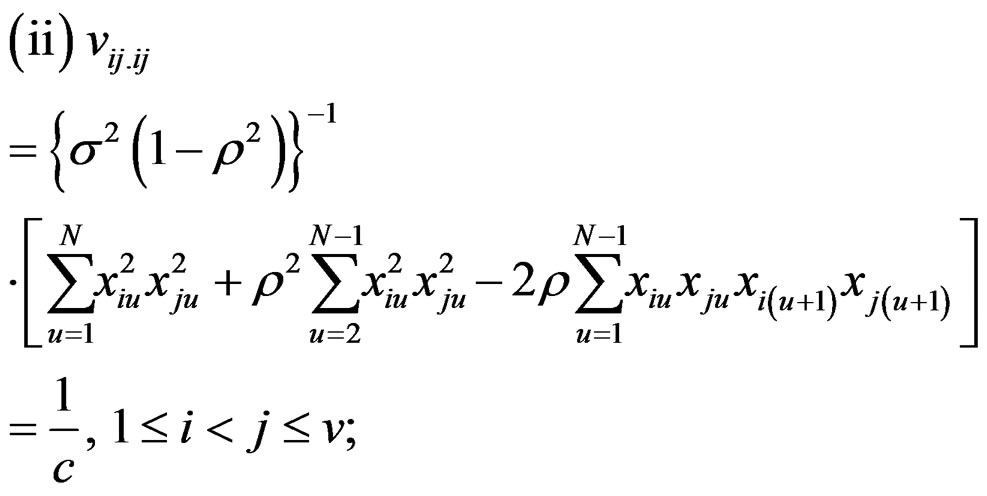
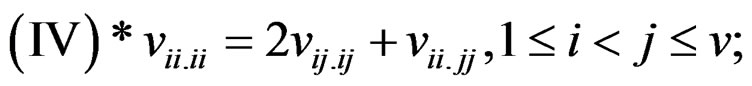 (8)
(8)
where 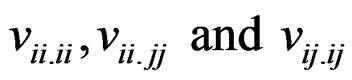 are as in (II)*(iii) and (III)*(i), (ii).
are as in (II)*(iii) and (III)*(i), (ii).
The condition for non-singularity is given by(V)* :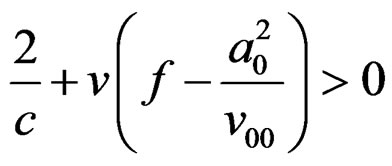 (9)
(9)
where 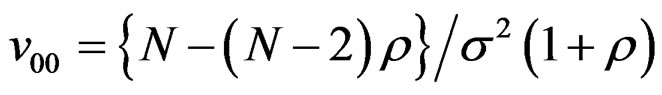 and
and 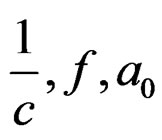
are as in (6).
Note: The conditions for exact rotatability, as stipulated above, are hard to satisfy in practice since ρ is unknown unless special efforts are made regarding choice of the underlying robust design. Towards this, tremendous simplification obtains whenever all odd moments of various types vanish. These are listed below for ready reference,
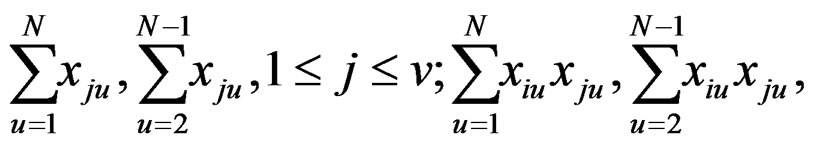
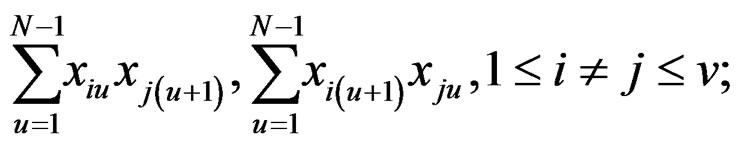

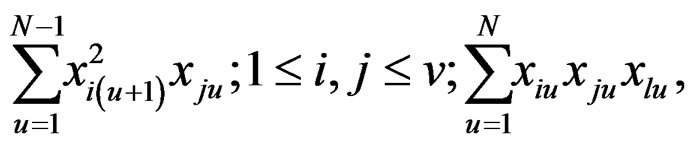
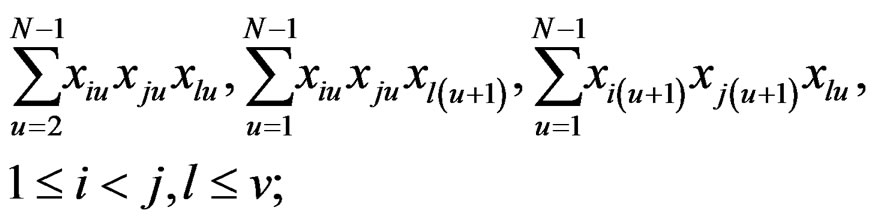
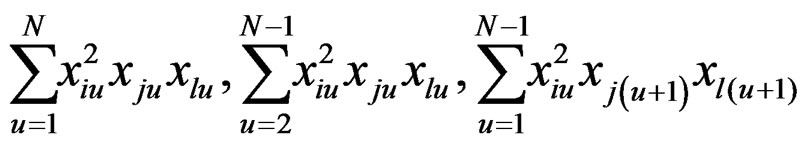
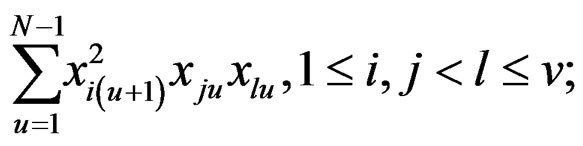
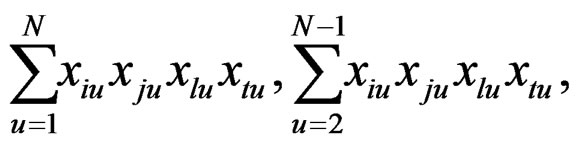

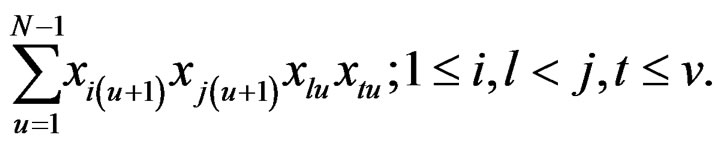 (10)
(10)
As to the even order moments (up to order 4) mere constancy of such moments (of various types) suffices to ensure exact rotatability. Specially, we desire to have each of the following terms independent of i and j:
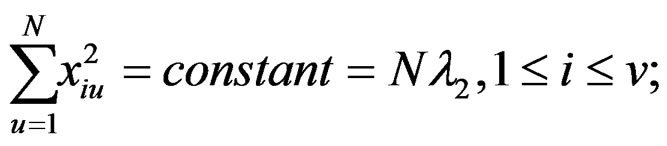
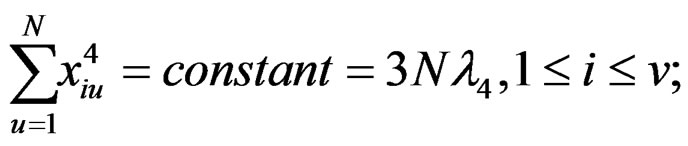
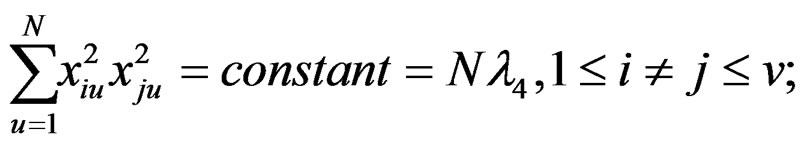
Using the above relations, for the newly constructed design, we get the following:
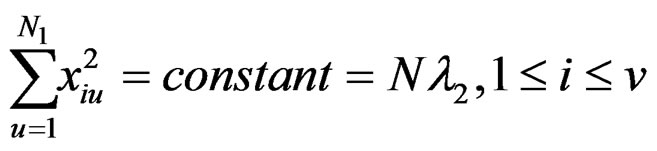

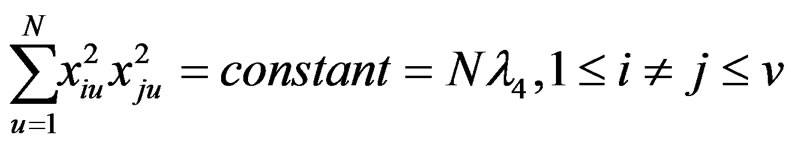 (11)
(11)
Thus, a design satisfying the conditions mentioned above may be successfully utilized as a rotatable design under violation of the homoscedasticity assumption subject to the covariance structure being of the type (conditions of exact rotatability). Such a design is, therefore, robust, where c, N, N1, 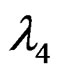 ,
,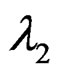 are constants.
are constants.
3. New Method of Construction of RSORD Using Balanced Incomplete Block Design
Here we start with usual SORD using BIBD having “n” non-central design points involving v-factors. The set of n design points can be extended to (2n + 1) points by incorporating (n + 1) central points in the following way.
One central point is placed in between each pair of noncentral design points in the sequence, resulting thereby in (n – 1) such central points. The other two central points are placed one at the beginning and one at the end.
If the number of central points of the usual SORD with which we started is greater than (n + 1), the remaining central points are placed in any manner, if the number is less, we need to include the requisite number of additional central points. Here we examine the non-singularity for the original design and the newly constructed design.
Let N be the number of design points of the original design (SORD) with which we started. Out of N, let n be the number of non-central design points and m be the number of central points i.e., N = n + m. In general m < n + 1, Let N1 be the number of design points of the newly constructed design, Where N1 = 2n + 1 > N. For the original design with which we started, the following are the moment relations:
Let (v, b, r, k, λ) denote a BIBD. 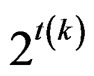 denote a fractional replicate of 2k in ±1 levels, in which no interaction with less than five factors is confounded and m be the number of central points in the design.
denote a fractional replicate of 2k in ±1 levels, in which no interaction with less than five factors is confounded and m be the number of central points in the design.
The design points for the newly constructed design are obtained as follows:
3.1. Method I: When r < 3λ
Here, 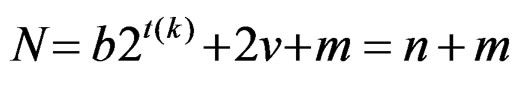 and N1 = 2n + 1, where
and N1 = 2n + 1, where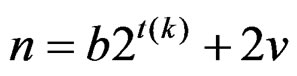 .
.
From the design points generated from the BIBD, simple symmetry conditions (10) and (11) are true. Conditions (10) are true obviously. Conditions (11) are true as follows:
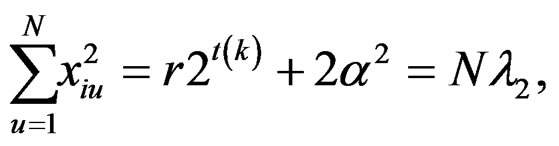
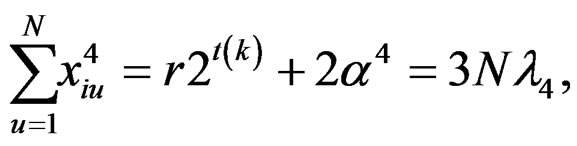
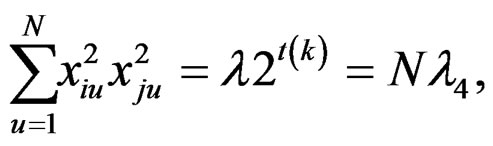
Using the above relations, for the newly constructed design, we get the following:
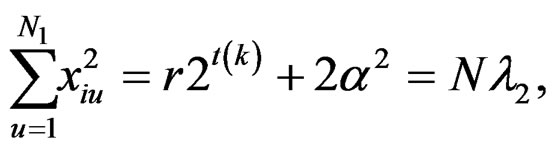
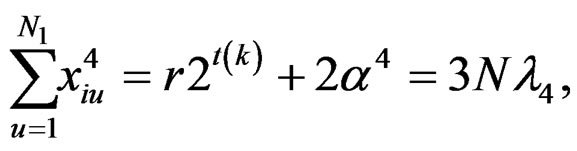
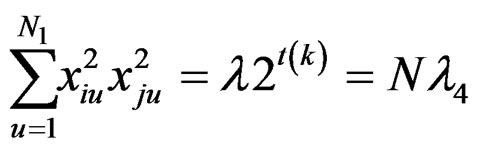 (12)
(12)
The results are given in Table 1.
3.2. Method II: When r = 3λ
Here, 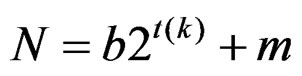 = n + m and N1 =2n + 1, where n=
= n + m and N1 =2n + 1, where n=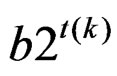 .
.
From the design points generated from the BIBD simple symmetry conditions (10) and (11) are true. Conditions (10) are true obviously. Conditions (11) are true as follows:
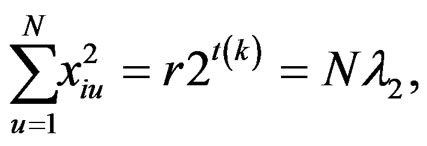

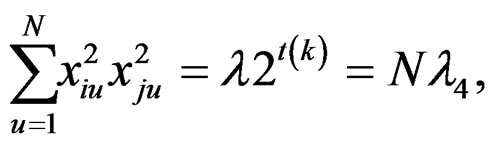
Using the above relations, for the newly constructed design, we get the following:
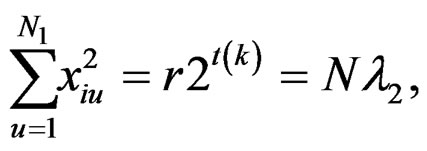
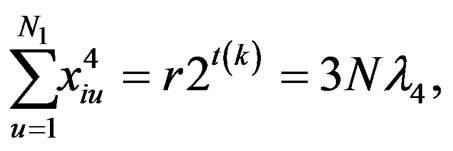
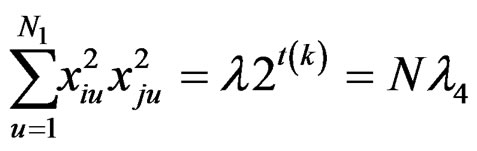 (13)
(13)
The results are given in Table 2.
3.3. Method III: When r > 3λ
Here,  = n + m and N1 = 2n + 1, Where n =
= n + m and N1 = 2n + 1, Where n = 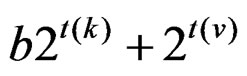
From the design points generated from the BIBD simple symmetry conditions (10) and (11) are true. Conditions (10) are true obviously. Conditions (11) are true as follows:
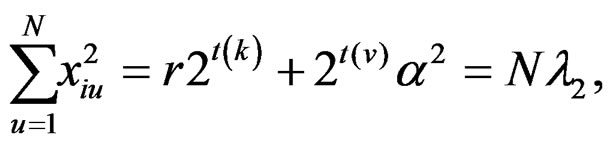


Table 1. Variance of the estimated response for the factors 3 ≤ v ≤ 8, when r < 3λ.

Table 2. Variance of the estimated response for the factors 3 ≤ v ≤ 8 , when r = 3λ.
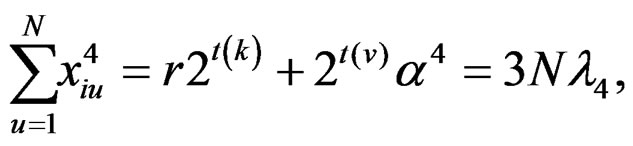
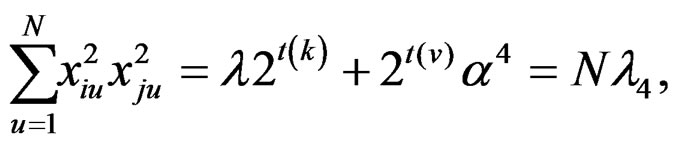
Using the above relations, for the newly constructed design, we get the following:
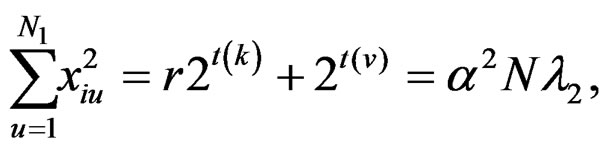
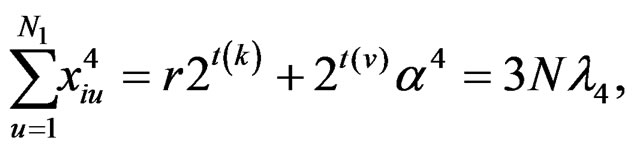
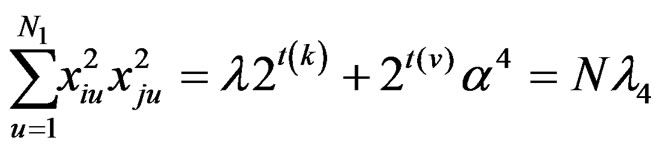 (14)
(14)
The results are given in Table 3.
(These expression follow easily from the definition of points sets generated from BIBD and their consequent multiplication with factorial combinations as explained in Raghavarao [7], pp. 298-300)
Using (5) and (12), (13), (14) the design parameters of the newly constructed design are the following:
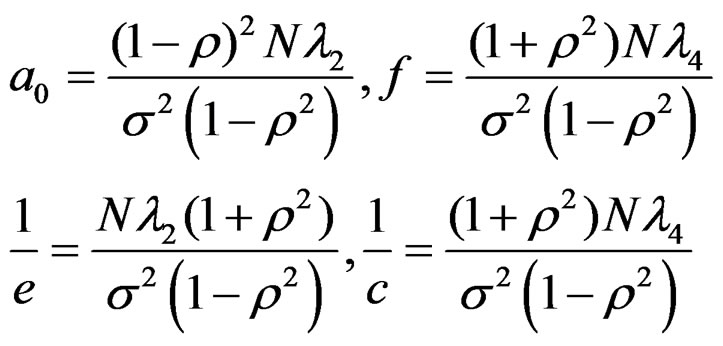 (15)
(15)
Using (15) and noting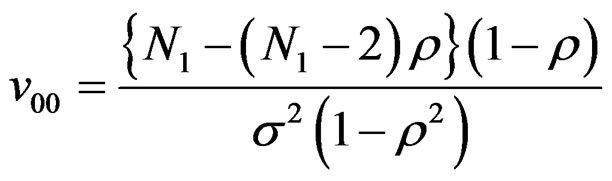 , the expression
, the expression 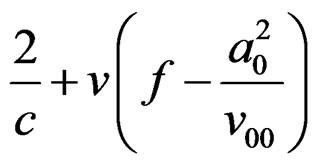 simplifies to
simplifies to
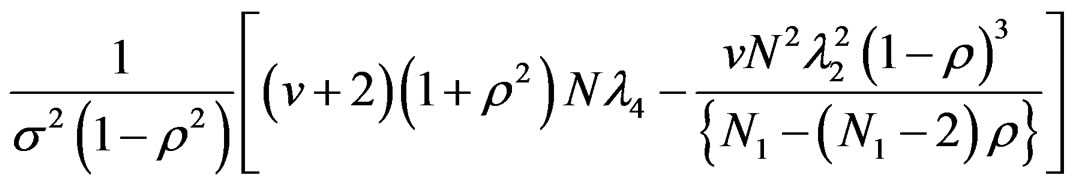
Hence the non-singularity condition of the above design is
 (16)
(16)
Let f (N, N1, ρ) =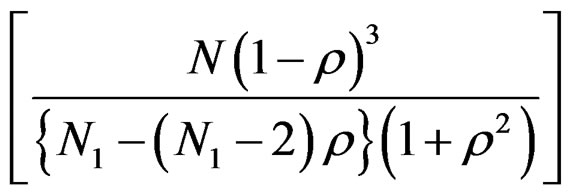

Table 3. Variance of the estimated response for the factors 3 ≤ v ≤ 8 , when r > 3λ.
It is readily seen that
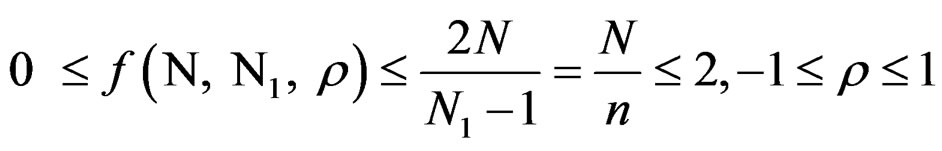
We now argue as follows, the design, to start with, is a SORD in the usual sense so that .
.
This condition indeed does satisfy the revised condition (16) derived here for ρ ≥ 0. To take care of all values of ρ, including negative values, it is enough to demand
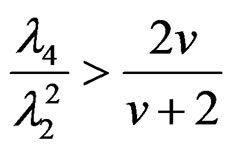 .
.
3.4. Variance Function
The variance function of SORDWCE under the autocorrelated structure constructed by the above method is obtained by using (7), and (16) and noting the following:
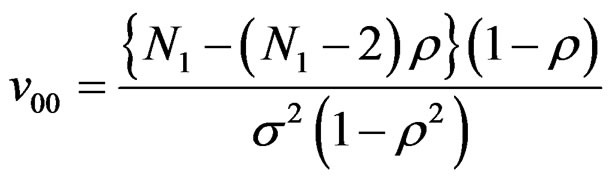
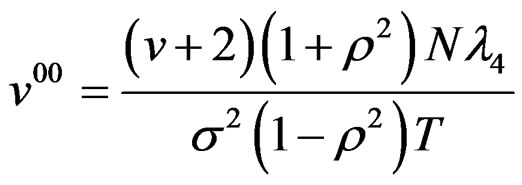
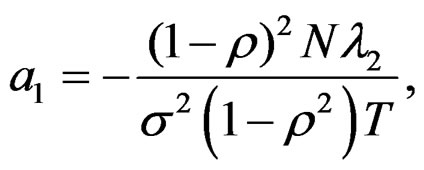
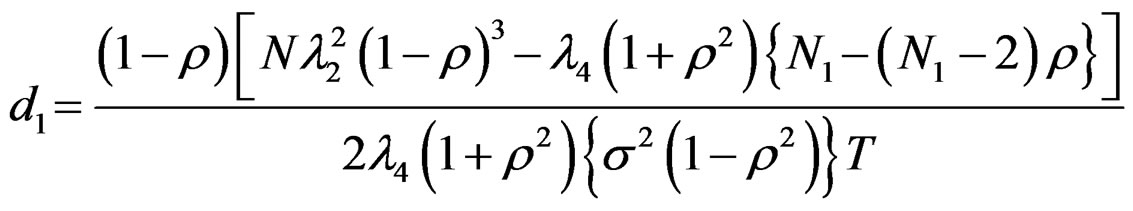
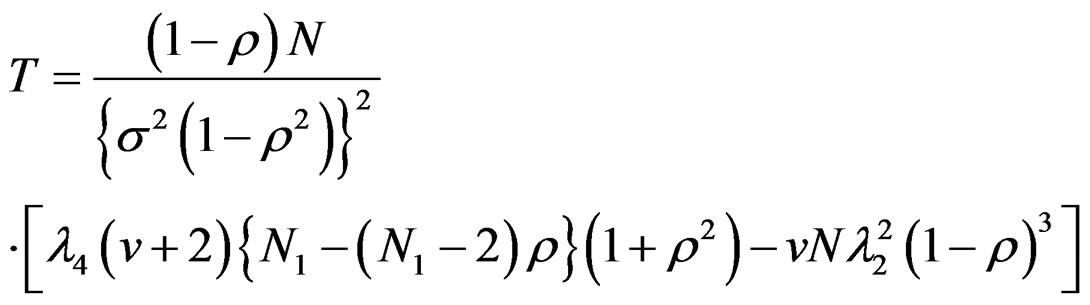
(17)
Hence the variance function is given by,
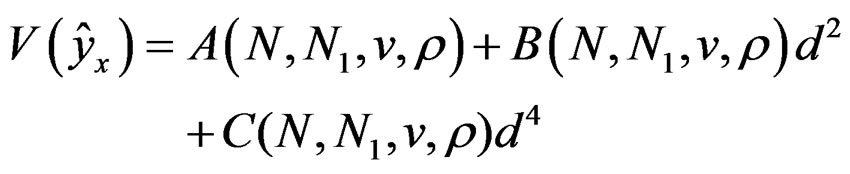 saywhere,
saywhere,
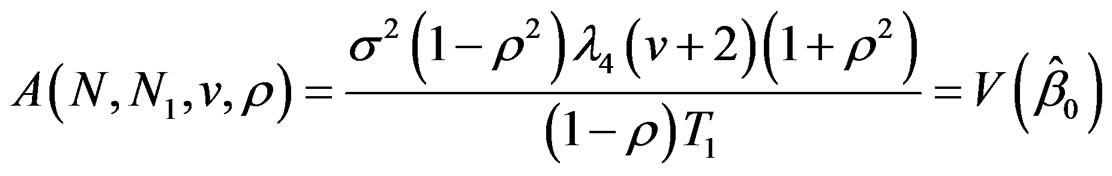
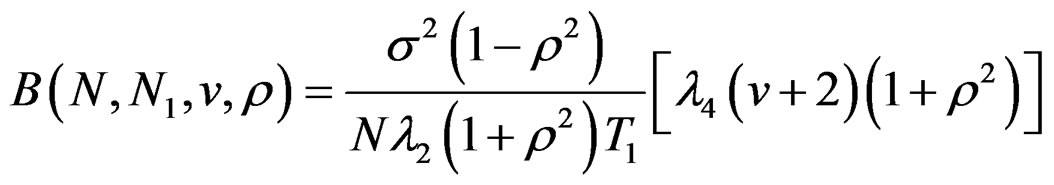


where
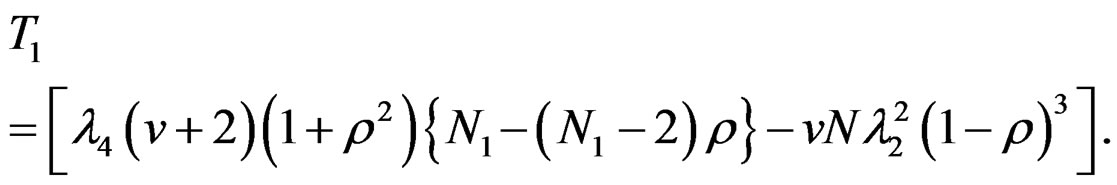
Example: We illustrate the above method with the construction of RSORD for 7-factors with the help of BIBD. Consider the BIBD (v = 7, b = 7, r = 3, k = 3, λ = 1). Here we have, N = 57, N1 = 113, n = 56, m = 1.
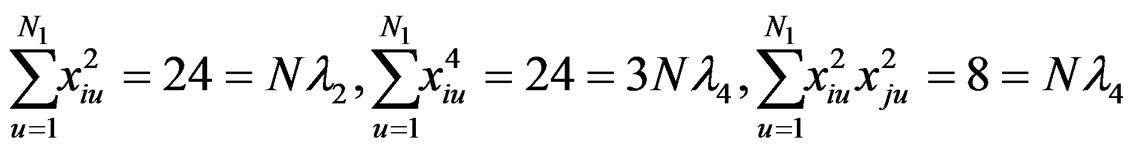
Plan of BIBD:
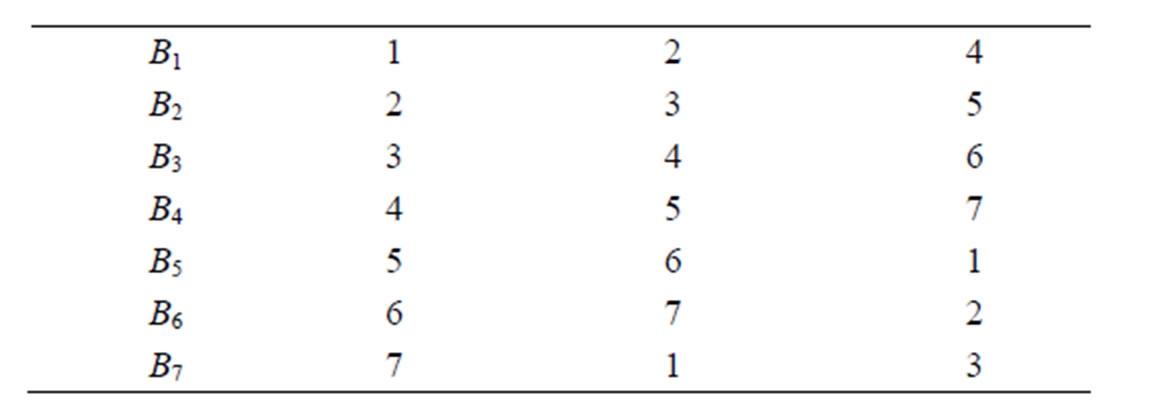
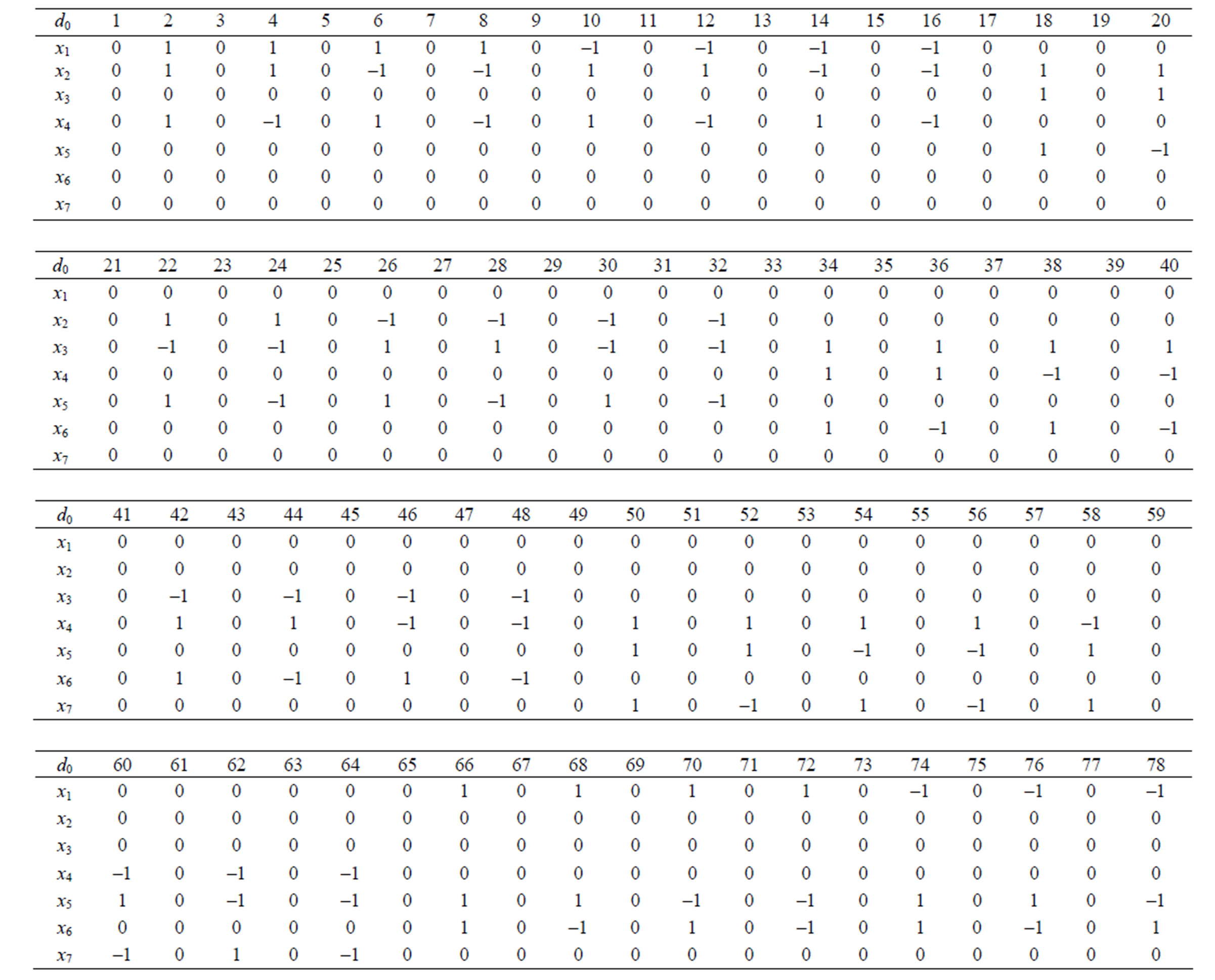
The design (denoted by d0) is displayed here for ready reference (column being runs).

As regards the non-singularity condition for this design, we note that 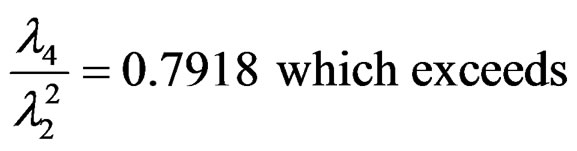
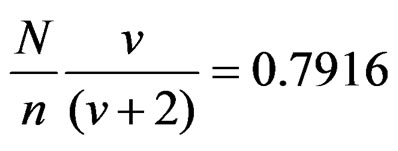 .
.
Hence the analysis of variance of estimated response for various factors 3 ≤ v ≤ 8 and it is achieved for all values of ρ, –1 ≤ ρ ≤ 1.
We may point out here that this RSORD has 113 design points for 7-factors where as the corresponding RRCCD obtained by Rajyalakshmi and Victorbabu [3] needs 157 design points. Thus the new method leads to a 7-factor RSORD in less number of design points than the corresponding RRCCD.
4. Acknowledgements
The authors are thankful to the referee and the editor for the valuable suggestions which helped in improving the quality of the paper.
REFERENCES
- R. N. Das, “Robust Second Order Rotatable Designs (Part I),” Calcutta Statistical Association Bulletin, Vol. 47, 1997, pp. 199-214.
- R. N. Das, “Robust Second Order Rotatable Designs (Part II),” Calcutta Statistical Association Bulletin, Vol. 49, 1999, pp. 65-78.
- K. Rajyalakshmi and B. Re, “Victorbabu, Robust Rotatable Central Composite Designs,” Paper Communicated for the Possible Publication, 2011.
- G. E. P. Box and J. S. Hunter, “Multifactor Experimental Designs for Exploring Response Surfaces,” Annals of Mathematical Statistics, Vol. 28, No. 1, 1957, pp. 195- 241. doi:10.1214/aoms/1177707047
- M. N. Das and V. L. Narasimham, “Construction of Rotatable Designs through Balanced Incomplete Block Designs,” Annals of Mathematical Statistics, Vol. 33, No. 4, 1962, pp. 1421-1439. doi:10.1214/aoms/1177704374
- R. N. Panda and R. N. Das, “First Order Rotatable Designs with Correlated Errors,” Calcutta Statistical Association Bulletin, Vol. 44, 1994, pp. 83-101.
- D. Raghavarao, “Construction and Combinatorial Problems in Design of Experiments,” John Wiley, New York. 1971.

