Open Journal of Statistics
Vol.1 No.3(2011), Article ID:8069,11 pages DOI:10.4236/ojs.2011.13020
Estimation of the Unknown Parameters for the Compound Rayleigh Distribution Based on Progressive First-Failure-Censored Sampling
Department of Mathematics, Umm Al-Qura University, Makkah Al-Mukarramah, KSA
E-mail: tabushal@yahoo.com
Received August 2, 2011; revised September 5, 2011; accepted September 17, 2011
Keywords: Compound Rayleigh Distribution, Progressive First-Failure Censored Scheme, Bayesian and Non-Bayesian Estimations, Approximate Confidence Intervals
Abstract
This article considers estimation of the unknown parameters for the compound Rayleigh distribution (CRD) based on a new life test plan called a progressive first failure-censored plan introduced by Wu and Kus (2009). We consider the maximum likelihood and Bayesian inference of the unknown parameters of the model, as well as the reliability and hazard rate functions. This was done using the conjugate prior for the shape parameter, and discrete prior for the scale parameter. The Bayes estimators have been obtained relative to both symmetric (squared error) and asymmetric (LINEX and general entropy (GE) loss functions. It has been seen that the symmetric and asymmetric Bayes estimators are obtained in closed forms. Also, based on this new censoring scheme, approximate confidence intervals for the parameters of CRD are developed. A practical example using real data set was used for illustration. Finally, to assess the performance of the proposed estimators, some numerical results using Monte Carlo simulation study were reported.
1. Introduction
There are many scenarios in life-testing and reliability experiments whose units are lost or removed from experimentation before failure. The loss may occur unintentionally, or it may have been designed so in the study. However, in many situations, the removal of units prior to failure is preplanned in order to provide saving in terms of time and cost associated with testing. There are many types of censored test, the most common censoring schemes are type-I and type-II censoring, but using this types of censoring can not allow for units to be removed from the test at any other point than the final termination point. However, if an experimenter desires to remove surviving units at points other than the final termination point of the life test, these two traditional censoring schemes will not be of use to the experimenter. The allowance of removing surviving units from the test before the final termination point is desirable, as in the case of studies of wear, in which the study of the actual aging process requires units to be fully disassembled at different stages of the experiment. In addition, when a compromise between the reduced time of experimentation and the observation of at least some extreme lifetimes is sought, such an allowance is also desirable. These reasons lead us into the area of progressive censoring.
It is well known that one of the primary goals of progressive censoring is to save some live units for other tests, which is particularly useful when the units being tested are very expensive. [1] mentioned that the inference is feasible, and practical when the sample data are gathered according to a Type-II progressively censored study experimental scheme. Statistical inferences on the parameters of failure time distributions under progressive censoring have been studied by several authors such as [1-12]. A recent account on progressive censoring schemes can be found in the book by [13], or in the excellent review by [14].
[15] described a life test in which the experimenter might decide to group the test units into several sets, each as an assembly of test units, and then run all the test units simultaneously until occurrence the first failure in each group. Such a censoring scheme is called first-failure censoring. [16] discussed a sampling plan for a bearing manufacturer. The bearing test engineer decided to save test time by testing 50 bearings in sets of 10 each, and the first-failure times from each group were observed. [17,18] discussed some inferences based on firstfailure-censored sampling from both the Gompertz distribution and Burr-XII distribution, respectively. Also see [19,20]. Note that a first-failure-censoring scheme is terminated when the first failure in each set is observed. If an experimenter desires to remove some sets of test units before observing the first failures in these sets this life test plan is called a progressive first-failure-censoring scheme which recently introduced by [21].
The two-parameter compound Rayleigh distribution (which is denoted by CRD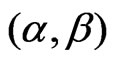 ) provides a population model which is useful in several areas of statistics, including life testing and reliability. The probability density function
) provides a population model which is useful in several areas of statistics, including life testing and reliability. The probability density function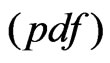 , and the cumulative distribution function
, and the cumulative distribution function 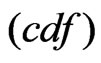 of CRD
of CRD 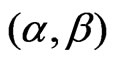 are given, respectively, by
are given, respectively, by
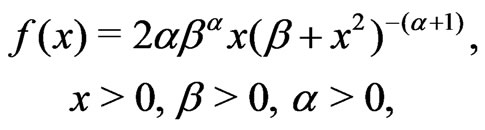 (1)
(1)
 , (2)
, (2)
and the reliability and failure rate functions, at some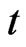 , are
, are
 ,
, 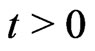 , (3)
, (3)
 ,
,  , (4)
, (4)
where 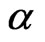 and
and 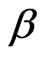 are the shape and the scale parameter respectively.
are the shape and the scale parameter respectively.
The compound Rayleigh distribution (CRD) is a special case of the 3- parameter Burr type XII distribution, which has a PDF of the form. The 2- parameter version of this distribution (with) was studied by several authors, such as [22-26], among others.
The main aim of this article is to focus on the designing problem of a progressive first-failure censoring life test with a compound Rayleigh failure time distribution. The rest of this article is organized as follows. In Section 2, the formulation of a progressive first-failure-censoring scheme is described. The ML estimations with the approximate confidence intervals of the parameters are obtained in Section 3. Bayesian estimations of the parameters, reliability and hazard rate functions of CRD based on progressive first-failure-censoring scheme are investigated in Section 4. In Section 5, for illustrative purposes, we performed a real data analysis. A simulation study in order to give an assessment of the performance of the estimation methods are presented in Section 6. Finally we conclude the paper in Section 7.
2. A Progressive First-Failure-Censoring Scheme
In this section, first-failure-censoring scheme is combined with the progressive censoring scheme as in [21]. Suppose that 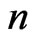 independent groups with
independent groups with  items within each group are put in a life test,
items within each group are put in a life test, 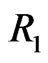 groups and the group in which the first failure is observed are randomly removed from the test as soon as the first failure (say
groups and the group in which the first failure is observed are randomly removed from the test as soon as the first failure (say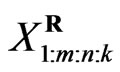 ) has occurred,
) has occurred, 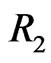 groups and the group in which the second first failure is observed are randomly removed from the test when the second failure (say
groups and the group in which the second first failure is observed are randomly removed from the test when the second failure (say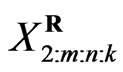 ) has occurred, and finally
) has occurred, and finally 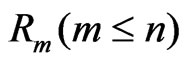 groups and the group in which the
groups and the group in which the 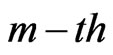 first failure is observed are randomly removed from the test as soon as the
first failure is observed are randomly removed from the test as soon as the 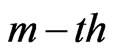 failure (say
failure (say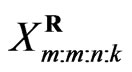 ) has occurred. The
) has occurred. The 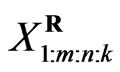
 are called progressively firstfailure-censored order statistics with the progressive censoring scheme
are called progressively firstfailure-censored order statistics with the progressive censoring scheme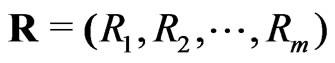 . It is clear that
. It is clear that  . If the failure times of the
. If the failure times of the  items originally in the test are from a continuous population with distribution function
items originally in the test are from a continuous population with distribution function 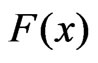 and probability density function
and probability density function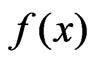 , the joint probability density function for
, the joint probability density function for 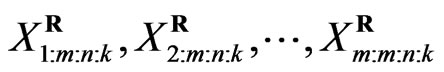 is given by
is given by
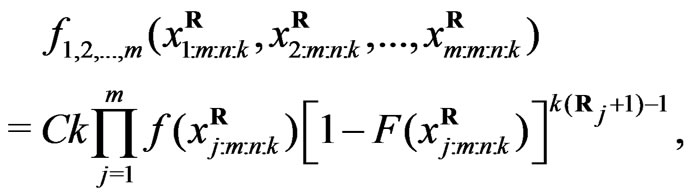 (5)
(5)
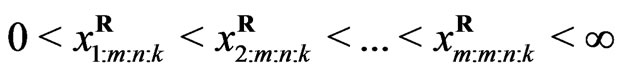 where
where
 (6)
(6)
It should be noted that 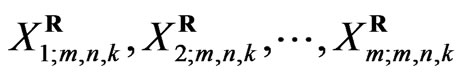 can be viewed as a progressive type II censored sample from a population with distribution function
can be viewed as a progressive type II censored sample from a population with distribution function 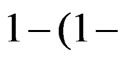
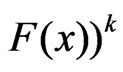 . For this reason, results for progressive type II censored order statistics can be extended to progressive first-failure censored order statistics easily. Also, the progressive first-failure censored plan has advantages in terms of reducing the test time, in which more items are used, but only
. For this reason, results for progressive type II censored order statistics can be extended to progressive first-failure censored order statistics easily. Also, the progressive first-failure censored plan has advantages in terms of reducing the test time, in which more items are used, but only 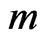 of
of 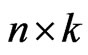 items are failures.
items are failures.
3. Maximum Likelihood Estimation
Based on progressively first-failure-censored sample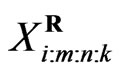 ,
, 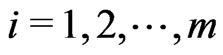 , with censoring scheme
, with censoring scheme 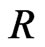 is drawn from the CRD (1). For convenience, we will denote the observed values of such sample by
is drawn from the CRD (1). For convenience, we will denote the observed values of such sample by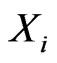 ,
,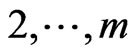
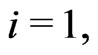 . From (5), the likelihood function is given by
. From (5), the likelihood function is given by
 (7)
(7)
where 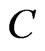 is defined in (6) The log-likelihood function is given by
is defined in (6) The log-likelihood function is given by
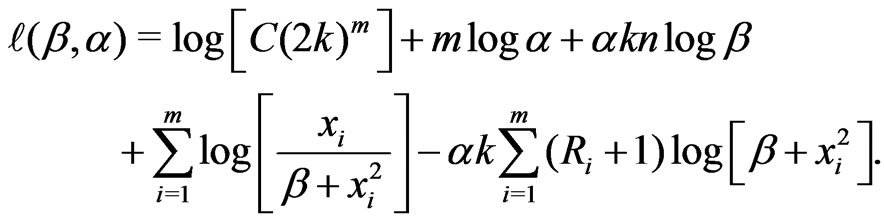 (8)
(8)
Calculating the first partial derivative of (8) with respect to 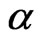 and
and  and equating to zero, we obtain the likelihood equations
and equating to zero, we obtain the likelihood equations
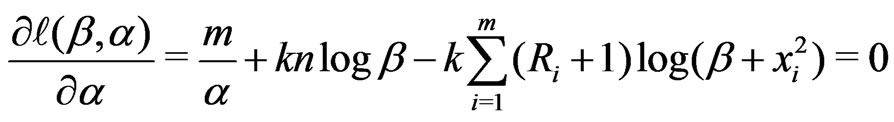 , (9)
, (9)
and
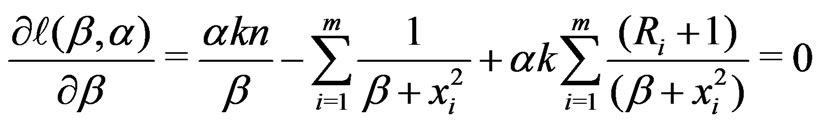 (10)
(10)
From (9), we have
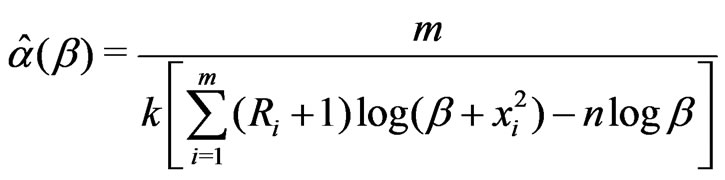 (11)
(11)
From (10) and (11), we have
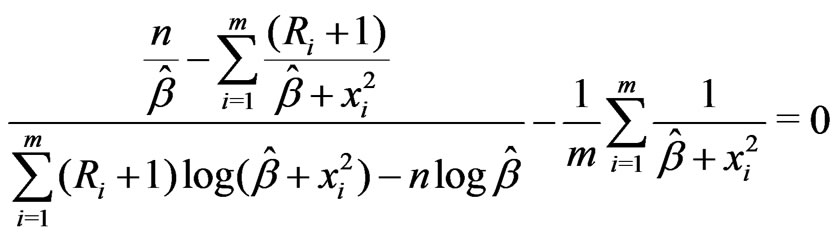 , (12)
, (12)
Newton-Raphson iteration is employed to solve (12). The corresponding MLE’s of the reliability function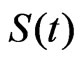 , and hazard rate function
, and hazard rate function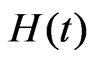 , are given respectively by (3) and (4) after replacing
, are given respectively by (3) and (4) after replacing 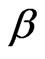 and
and 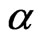 by their MLE’s
by their MLE’s  and
and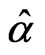 . To obtain a starting value for the root finding method, we can use the graphical method discussed in [27].
. To obtain a starting value for the root finding method, we can use the graphical method discussed in [27].
Approximate Interval Estimation
From the log-likelihood function in (8), we have
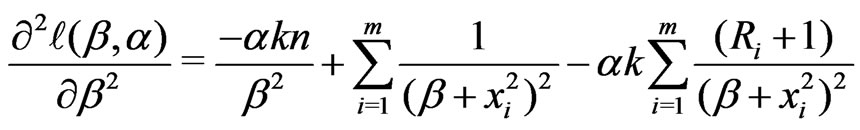 . (13)
. (13)
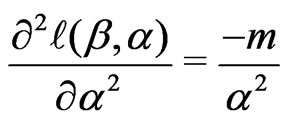 (14)
(14)
and
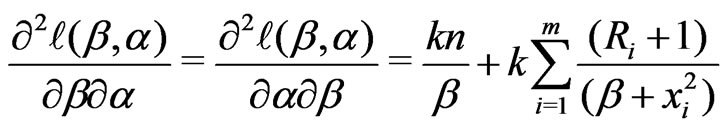 . (15)
. (15)
Let  denote a progressively first-failure-censored sample from the CRD with parameters
denote a progressively first-failure-censored sample from the CRD with parameters 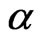 and
and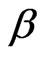 . The Fisher information matrix
. The Fisher information matrix 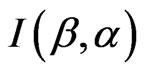 is then obtained by taking expectation of minus Equations (13)-(15). Under some mild regularity conditions,
is then obtained by taking expectation of minus Equations (13)-(15). Under some mild regularity conditions, 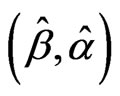 is approximately bivariate normal with mean
is approximately bivariate normal with mean 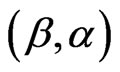 and covariance matrix
and covariance matrix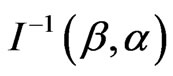 . In practice, we usually estimate
. In practice, we usually estimate 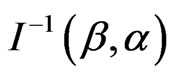 by
by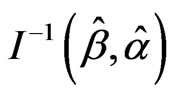 . A simpler and equally valied procedure is to use the approximation
. A simpler and equally valied procedure is to use the approximation
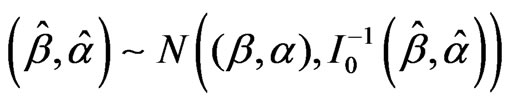 , (16)
, (16)
where 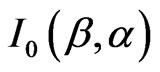 is the observed information matrix given by
is the observed information matrix given by
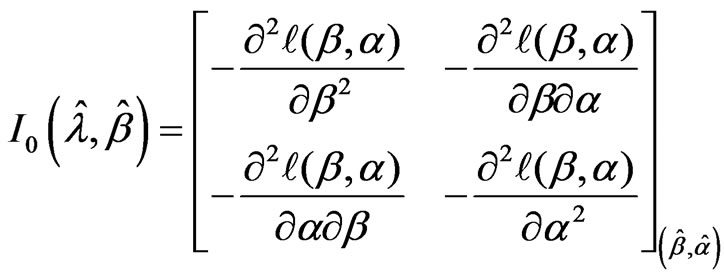 . (17)
. (17)
Approximate confidence intervals for 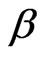 and
and 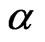 can be found by to be bivariate normal with mean
can be found by to be bivariate normal with mean 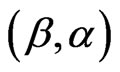 and covariance matrix
and covariance matrix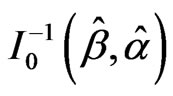 . Thus, a
. Thus, a 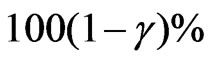 approximate confidence intervals for
approximate confidence intervals for 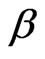 and
and 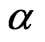 are
are
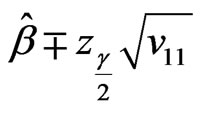 and
and 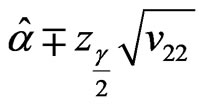 (18)
(18)
respectively, where 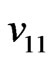 and
and 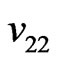 are the elements on the main diagonal of the covariance matrix
are the elements on the main diagonal of the covariance matrix 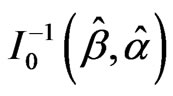
and  is the percentile of the standard normal distribution with right-tail probability
is the percentile of the standard normal distribution with right-tail probability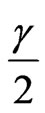 .
.
4. Bayes Estimation
In this section, we present the posterior densities of the parameters 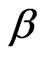 and
and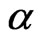 , and obtain symmetric and asymmetric Bayes estimators for the parameters, reliability and hazard rate functions.
, and obtain symmetric and asymmetric Bayes estimators for the parameters, reliability and hazard rate functions.
4.1. The Loss Function
For Bayesian approach, in order to select a single value as representing our “best” estimators of the unknown parameter, a loss function must be specified. A wide variety of loss functions has been developed in literature to describe various types of loss structures. The symmetric square-error loss (SE) is one of the most popular loss functions. It is widely employed in the inference, but its application is motivated by its good mathematical properties, not by its applicability to representing a true loss structure. A loss function should represent the consequences of different errors. There are situations where overand under-estimation can lead to different consequences. For example, when we estimate the average reliable working life of the components of a spaceship or an aircraft, over-estimation is usually more serious than underestimation. Being symmetric, the SE loss equally penalizes overand under-estimation of the same magnitude. A useful asymmetric loss known as the LINEX loss function, was introduced by [28], and was widely used in several papers, see for example, [5,6,10,11,28- 30]. This function rises approximately exponentially on one side of zero, and approximately linearly on the other side. Under the assumption that the minimal loss occurs at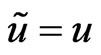 , the LINEX loss function for
, the LINEX loss function for 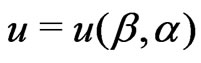 can be expressed as
can be expressed as
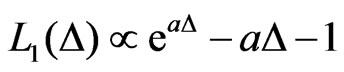 ,
, 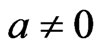 , (19)
, (19)
where 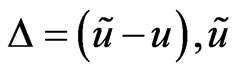 is an estimate of
is an estimate of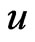 .
.
The sign, and magnitude of the shape parameter 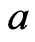 represent the direction and degree of symmetry respectively (if
represent the direction and degree of symmetry respectively (if , overestimation is more serious than underestimation and
, overestimation is more serious than underestimation and 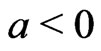 means the opposite). For
means the opposite). For 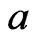 close to zero, the LINEX loss function is approximately the squared error loss (SEL) and therefore almost symmetric.
close to zero, the LINEX loss function is approximately the squared error loss (SEL) and therefore almost symmetric.
The posterior expectation of the LINEX loss function of (19) is
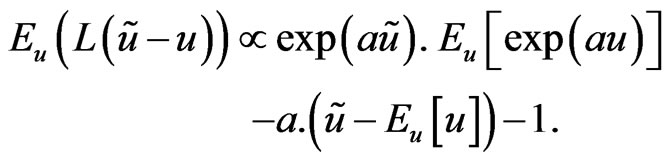 (20)
(20)
where  is denotes posterior expectation with respect to the posterior
is denotes posterior expectation with respect to the posterior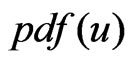 . The Bayes estimator
. The Bayes estimator 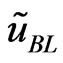 of
of 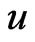 under the LINEX loss function is the value
under the LINEX loss function is the value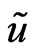 , which minimizes (20), it is
, which minimizes (20), it is
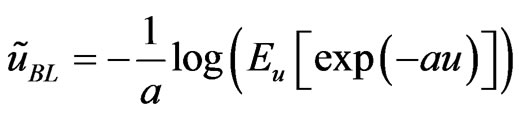 (21)
(21)
provided that the expectation 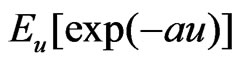 exists and is finite.
exists and is finite.
Another useful asymmetric loss function is the general entropy loss (GEL)
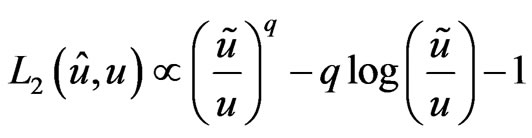 (22)
(22)
whose minimum occurs at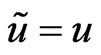 . This loss function is a generalization of the entropy-loss used in several papers where
. This loss function is a generalization of the entropy-loss used in several papers where 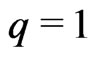 by [31] and [32]. When
by [31] and [32]. When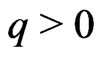 , a positive error (
, a positive error (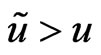 ) causes more serious consequences than a negative error. The Bayes estimate
) causes more serious consequences than a negative error. The Bayes estimate  of
of 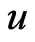 under GE loss (22) is
under GE loss (22) is
 (23)
(23)
provided that 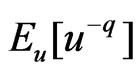 exists, and is finite.
exists, and is finite.
4.2. Prior Distribution and Posterior Analysis
In this section we first describe the prior information needed for the Bayesian analysis of the unknown parameters. When the parameters  and
and 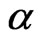 are assumed to be unknown, the following idea of [33], we assume that the parameter
are assumed to be unknown, the following idea of [33], we assume that the parameter 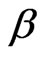 has a discrete prior, while the conditional distribution of
has a discrete prior, while the conditional distribution of 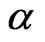 given
given 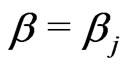 has a conjugate gamma prior. Now, we suppose that the parameter
has a conjugate gamma prior. Now, we suppose that the parameter 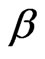 is restricted to a finite number of values, say
is restricted to a finite number of values, say  in the interval
in the interval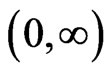 , i.e.
, i.e.
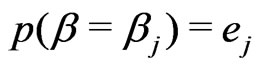 ,
, 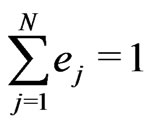 and
and ,
,
 . Further, suppose that conditional upon
. Further, suppose that conditional upon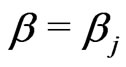 ,
, 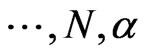
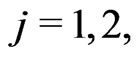 has a natural conjugate gamma
has a natural conjugate gamma 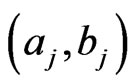 prior, with density
prior, with density
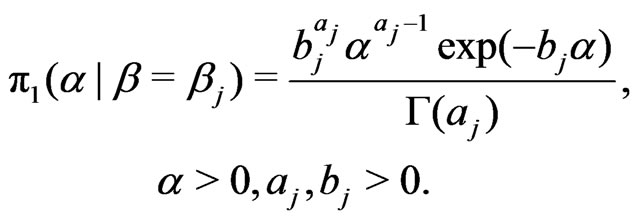 (24)
(24)
Combining the likelihood function in (5), and prior density (24), we obtain the marginal posterior probability of  conditional
conditional 
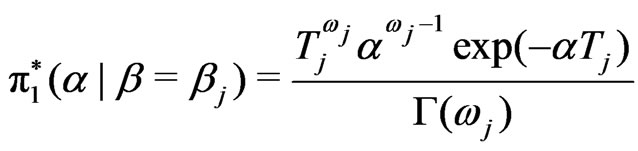 , (25)
, (25)
where
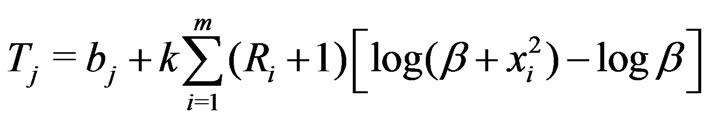 ,
, . (26)
. (26)
On applying the discrete version of Bayes theorem, the marginal posterior probability distribution of  is given by
is given by
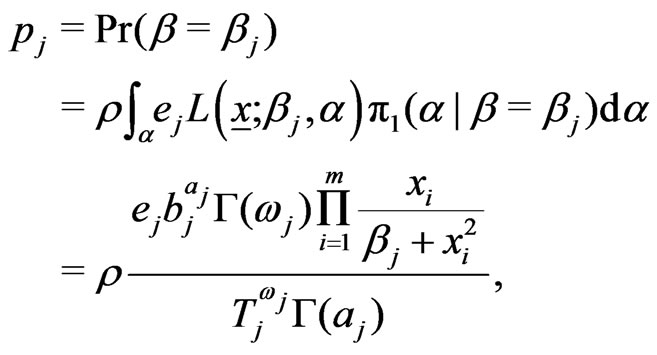 (27)
(27)
where  and
and  given by (26) and
given by (26) and 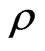 is a normalized constant given by
is a normalized constant given by
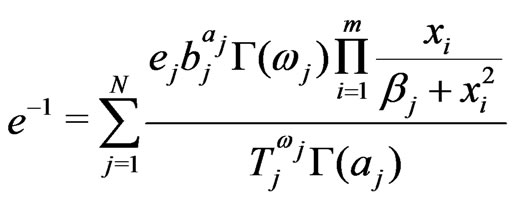 . (28)
. (28)
The joint posterior probability of  and
and  is
is
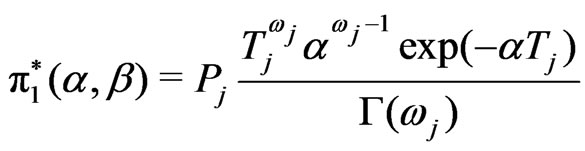 ,
,  ,
,  ,
, . (29)
. (29)
4.3. Symmetric Bayes Estimation
By using posterior denisties in (25) and (27), the Bayes estimators ,
,  ,
, 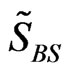 , and
, and 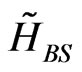 of the parameters
of the parameters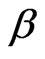 ,
, 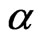 ,
,  reliability function
reliability function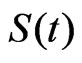 , and hazard rate function
, and hazard rate function 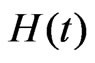 relative to ESL function, are, respectively
relative to ESL function, are, respectively
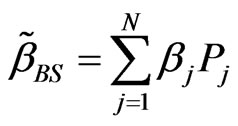 ,
,  , (30)
, (30)
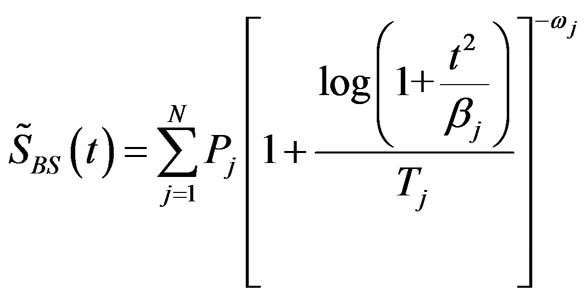 , (31)
, (31)
and
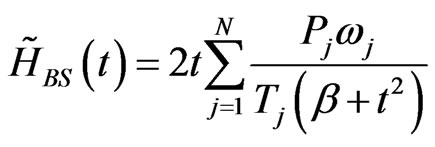 . (32)
. (32)
4.4. Asymmetric Bayes Estimation
4.4.1. LINEX Loss Function
Based on progressively first-failure censored data, the Bayes estimators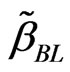 ,
, 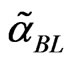 ,
, 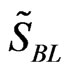 , and
, and 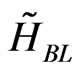 of the parameters
of the parameters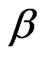 ,
,  ,
,  reliability function
reliability function , and hazard rate function
, and hazard rate function 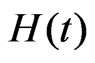 relative to LINEX loss function, are, respectively
relative to LINEX loss function, are, respectively
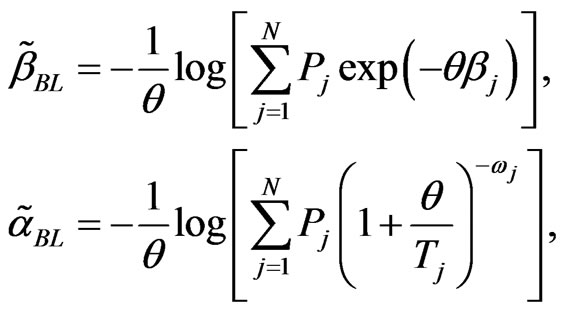 (33)
(33)
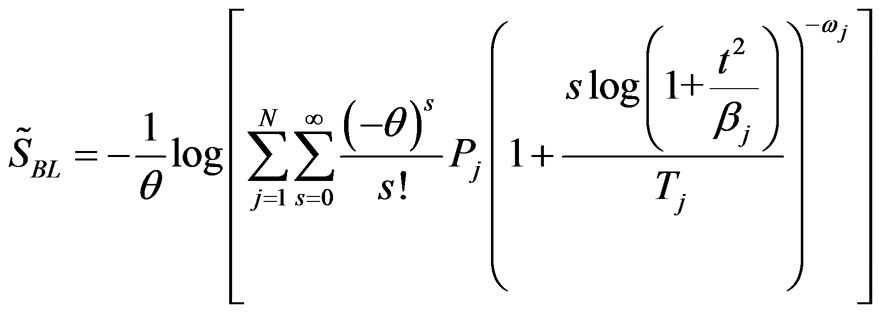 (34)
(34)
and
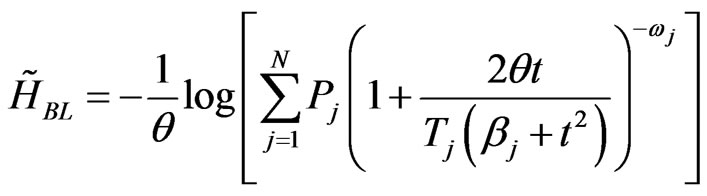 . (35)
. (35)
4.4.1. GE Loss Function
Also, by using posterior denisties (25) and (27), the Bayes estimators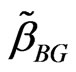 ,
, 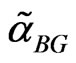 ,
, 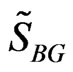 , and
, and 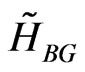 of the parameters
of the parameters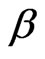 ,
, 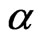 ,
, 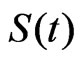 , and
, and , relative to GE loss function, are, respectively
, relative to GE loss function, are, respectively
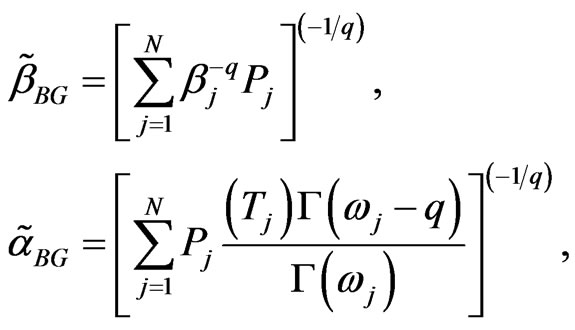 (36)
(36)
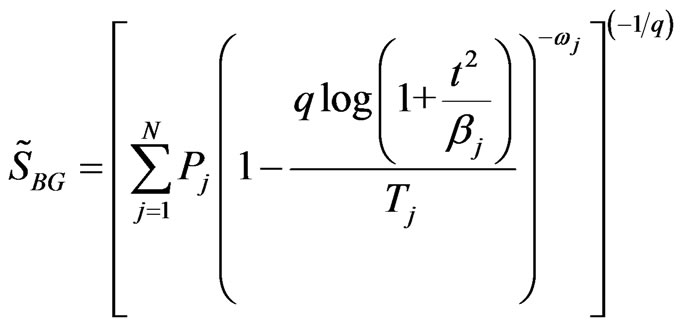 , (37)
, (37)
and
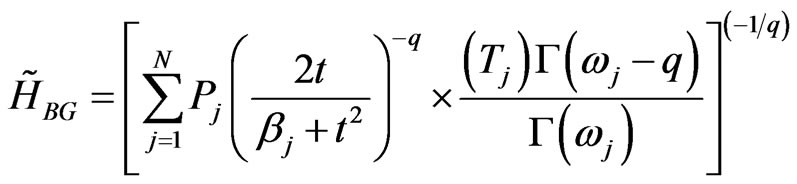 . (38)
. (38)
To implement the calculations in this subsections, it is first necessary to elicit the values of 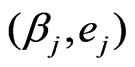 and the hyperparameters
and the hyperparameters 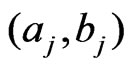 in the prior (25), for
in the prior (25), for 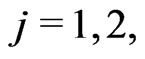
 . The former paris of values are fairly straightforward to specify, but for (
. The former paris of values are fairly straightforward to specify, but for (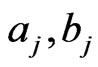 ) it is necessary to condition prior beliefs about
) it is necessary to condition prior beliefs about 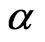 on each
on each 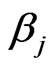 in turn, and this can be difficult in practice, an alternative method for obtaining the values
in turn, and this can be difficult in practice, an alternative method for obtaining the values 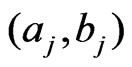 can be based on the expected value of the reliability function
can be based on the expected value of the reliability function 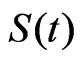 conditional on
conditional on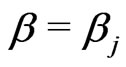 , see [34], which is given using (25) by
, see [34], which is given using (25) by
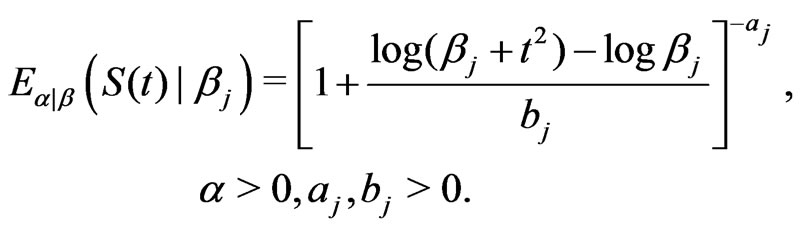 (39)
(39)
Now, suppose that prior beliefs about the lifetime distribution enable one to specify two values ,
, . Thus, for these two prior values
. Thus, for these two prior values 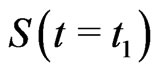 and
and , the values of
, the values of 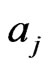 and
and 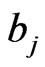 for each value
for each value 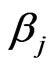 can be obtained numerically from (43). If no prior beliefs, a nonparametric procedure can be used to estimate the corresponding two different values of
can be obtained numerically from (43). If no prior beliefs, a nonparametric procedure can be used to estimate the corresponding two different values of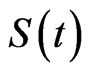 , see [35].
, see [35].
5. Data Analysis
For illustrative purposes, we performed a real data analysis. The original data is a subset of data reported by [6,36], represent the survival times in years of a group of patients given chemotherapy treatment alone. The data consisting of 46 survival times (in years) for 46 patients are: 0.047, 0.115, 0.121, 0.132, 0.164, 0.197, 0.203, 0.260, 0.282, 0.296, 0.334, 0.395, 0.458, 0.466, 0.501, 0.507, 0.529, 0.534, 0.540, 0.570, 0.641, 0.644, 0.696, 0.841, 0.863, 1.099, 1.219, 1.271, 1.326, 1.447, 1.485, 1.553, 1.581, 1.589, 2.178, 2.343, 2.416, 2.444, 2.825, 2.830, 3.578, 3.658, 3.743, 3.978, 4.003, 4.033. [6,36] show that the Compound Rayleigh model is acceptable for these data. Now, we suppose that the forty six patients are randomly grouped into 23 sets, with two patients in each ( ), and the survival times for all sets are observed and listed in ascending order in Table 1. In this example, based on survival times of the 23 sets given in Table 1, with
), and the survival times for all sets are observed and listed in ascending order in Table 1. In this example, based on survival times of the 23 sets given in Table 1, with 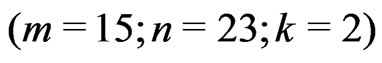 and the censoring scheme
and the censoring scheme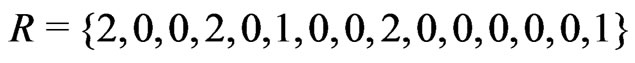 , we obtain the following progressive first-fauilure censoring data: 0.047, 0.115, 0.121, 0.164, 0.197, 0.26, 0.282, 0.334, 0.395, 0.458, 0.529, 0.534, 0.641, 0.6961.099.
, we obtain the following progressive first-fauilure censoring data: 0.047, 0.115, 0.121, 0.164, 0.197, 0.26, 0.282, 0.334, 0.395, 0.458, 0.529, 0.534, 0.641, 0.6961.099.
To compute the Bayes estimates. Firstly, we estimate two values of the reliability function using a nonparametric procedures.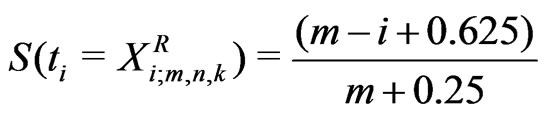 ,
, 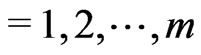
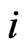 , see [37]. In our case, we use
, see [37]. In our case, we use 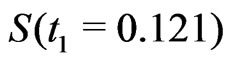
 and
and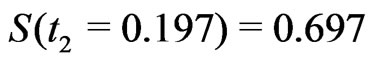 . These two prior probabilities are substituted into (39), where
. These two prior probabilities are substituted into (39), where 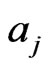 and
and 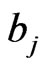 are solved numerically for each given
are solved numerically for each given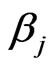 ,
, 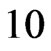
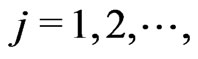 using Newton-Raphson method. Table 2 summarized the values of
using Newton-Raphson method. Table 2 summarized the values of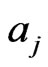 ,
, 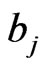 and
and 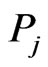 for each given
for each given 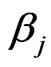 and
and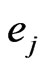 ,
,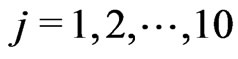 .
.
Using our results in Sections 3 and 4, the MLE estimates and the Bayes estimates of 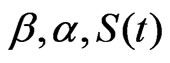 and
and 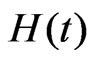 have been computed and the results are displayed in Table 3. By using (18) the 95% approximate confidence interval of
have been computed and the results are displayed in Table 3. By using (18) the 95% approximate confidence interval of 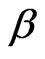 and
and 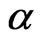 are, respectively (–0.3148, 0.8027) and (–0.3958, 1.7547).
are, respectively (–0.3148, 0.8027) and (–0.3958, 1.7547).
6. Simulation Study
Since the performance of the different methods cannot be compared theoretically, we perform Monte Carlo simula-

Table 1. Randomly grouped sets using data from Stablein (1981).

Table 2. Prior information, hyper parameter values and the posterior probabilities.

Table 3. The ML and the Bayes estimates of ,
,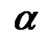 ,
,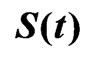 and
and with
with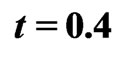 .
.
tions to compare the performances of the different estimators for different sampling schemes. All the computations are performed with a Pentium IV processor using Mathematica 8.0. We used different sample sizes (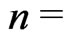 number of groups), different group sizes (
number of groups), different group sizes (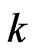 ), different effective sample sizes (
), different effective sample sizes ( ), and different sampling schemes (i.e., different
), and different sampling schemes (i.e., different  values).We used two sets of parameter values:
values).We used two sets of parameter values: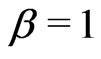 ,
, 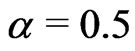 and
and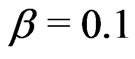 ,
, 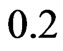
 , mainly to compare the MLEs and different Bayes estimators in terms of their mean squared errors (MSEs), and also to explore their effects on different parameter values.
, mainly to compare the MLEs and different Bayes estimators in terms of their mean squared errors (MSEs), and also to explore their effects on different parameter values.
To generate progressive firstfailure censored samples from CRD, we used the algorithm proposed by [13], with the fact that, the progressive first-failure censored sample 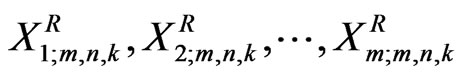 with distribution function
with distribution function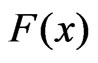 , can be viewed as a progressive type II censored sample from a population with distribution function
, can be viewed as a progressive type II censored sample from a population with distribution function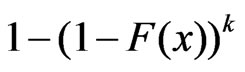 . We assume that the number of items putting in a life test is (
. We assume that the number of items putting in a life test is (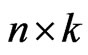 ) items, where
) items, where 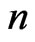 denotes the number of groups and
denotes the number of groups and  denotes the number of items in each group. Using a progressive first-failure censoring scheme, only
denotes the number of items in each group. Using a progressive first-failure censoring scheme, only 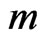 observations are record from the test. To compare the performances of the estimation procedures developed in this paper, we consider the following three progressive censoring schemes (
observations are record from the test. To compare the performances of the estimation procedures developed in this paper, we consider the following three progressive censoring schemes (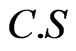 ), namely:
), namely:
Scheme I: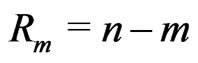 ,
,  for
for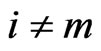 .
.
Scheme II: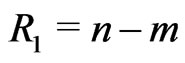 ,
, 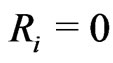 for
for .
.
Scheme III: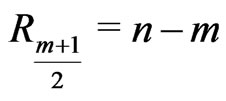 ,
, 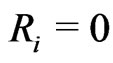 for
for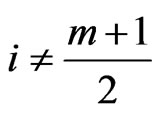 ; if
; if
 odd, and
odd, and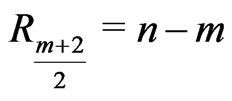 ,
, 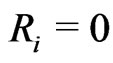 for
for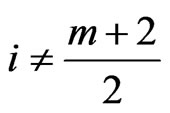 ; if
; if 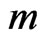 even.
even.
The three censoring schemes are corresponding, respectively, to the cases of all surviving items are removed from the experiment at the last failure point, first failure point and midpoint. Also, it should be noted that scheme I is the Type-II first-failure censored scheme.
In Tables 4-7, we report the mean squared errors (MSEs) of the ML estimates and different Bayes estimates of the parameters, reliability and hazard rate functions, based on 1000 replications. The results are reported in Tables 4 and 5 for the parameters values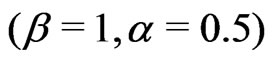 . Tables 6 and 7 display the same results for the parameters values
. Tables 6 and 7 display the same results for the parameters values .
.
7. Conclusions
In this paper, the maximum likelihood and Bayes methods are used for estimating parameters, reliability function and hazard rate function of the CRD based on a new censoring scheme, called a progressive first-failure censoring scheme. Combining the concept of first-failure censoring and the concept of progressive censoring, a

Table 4. MSEs of estimates of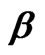 and
and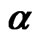 when (
when ( ,
,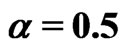 ;
; ).
).
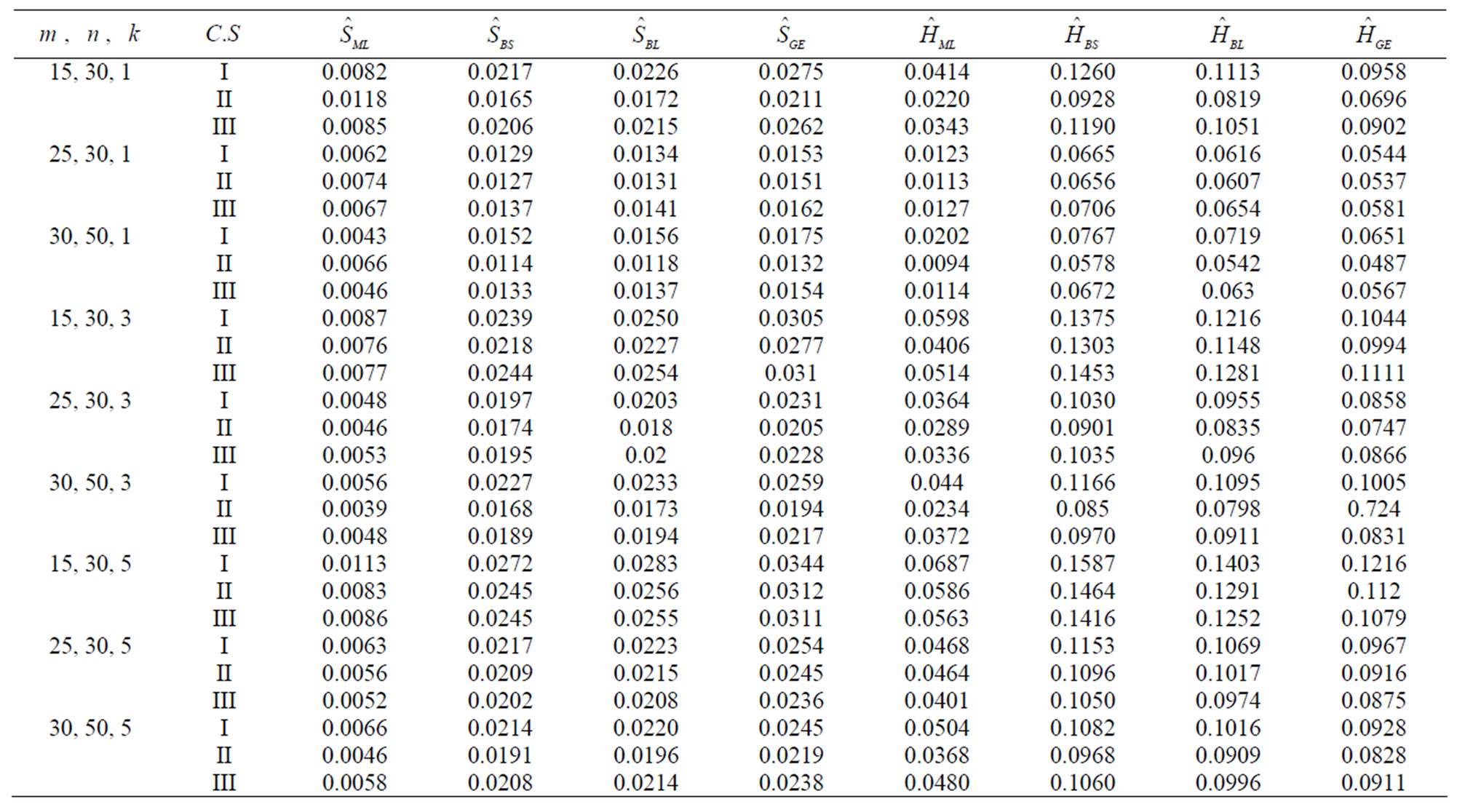
Table 5. MSEs of estimates of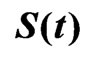 and
and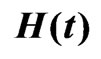 when (
when (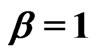 ,
,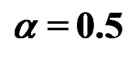 ;
;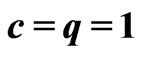 and
and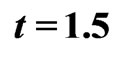 ).
).
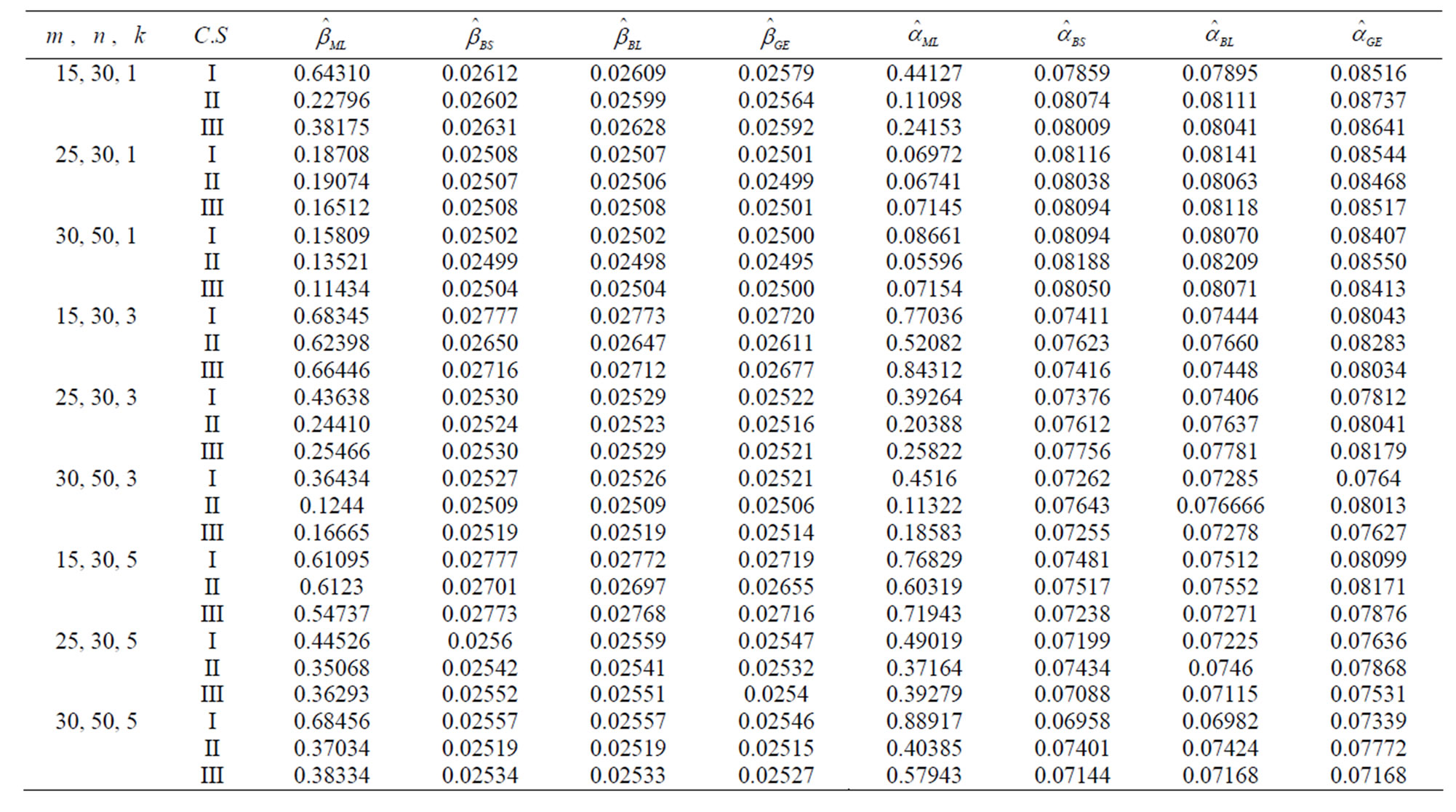
Table 6. MSEs of estimates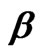 and
and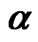 with (
with (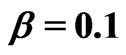 ,
,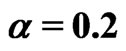 ;
;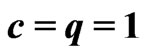 ).
).
progressive first-failure censoring scheme has been introduced by [21]. This censoring scheme has advantages in terms of reducing test time, in which more items are used but only  of (
of (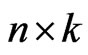 ) items are failures. Based on this new censoring scheme, the present paper shows how the things can be routinely managed for the CRD in a
) items are failures. Based on this new censoring scheme, the present paper shows how the things can be routinely managed for the CRD in a
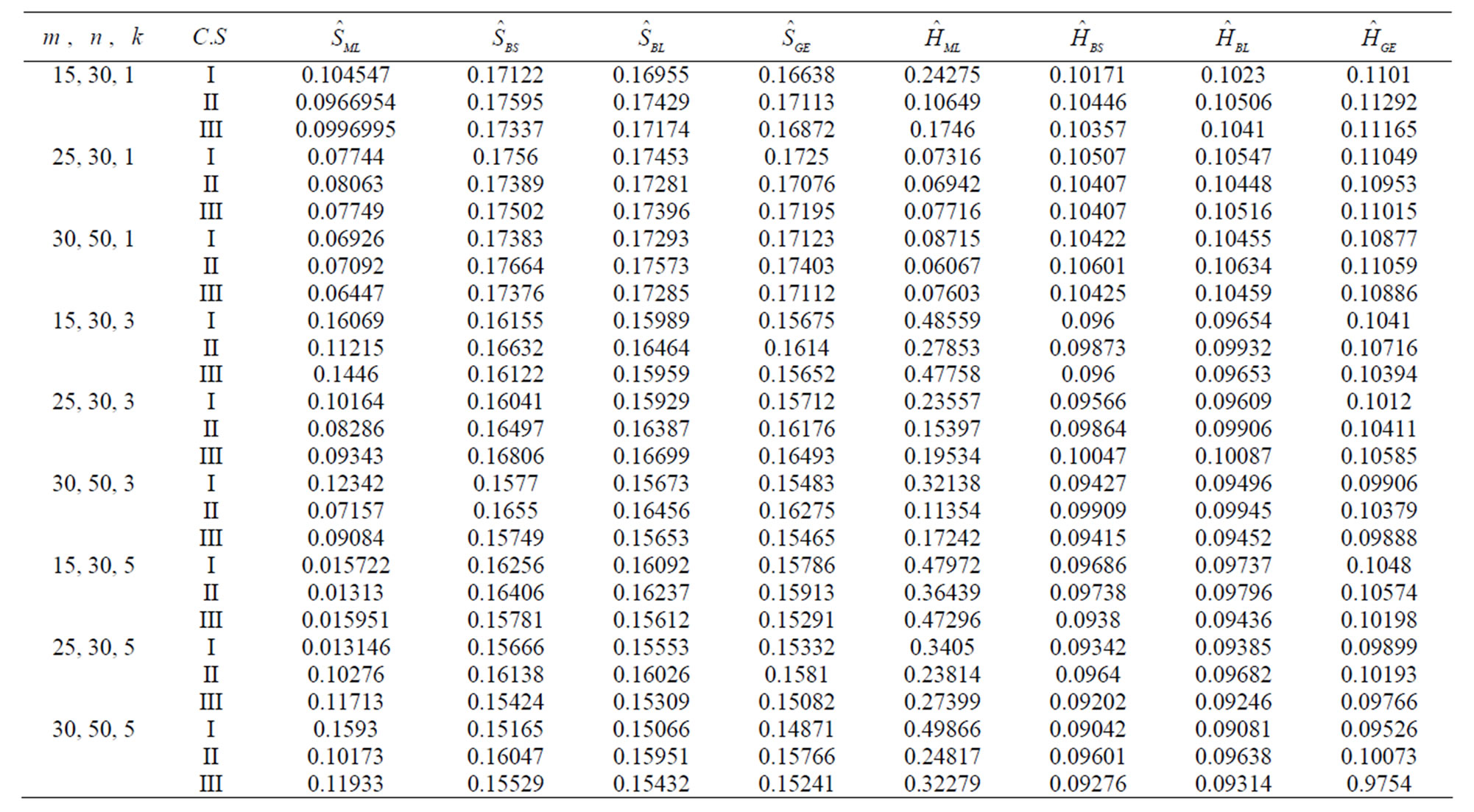
Table 7. MSEs of estimates of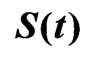 and
and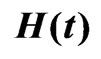 when (
when (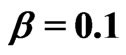 ,
,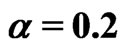 ;
;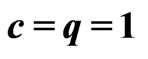 and
and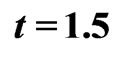 ).
).
Bayesian and classical frameworks. We have considered the maximum likelihood (ML) and Bayes estimates for the parameters of the CRD, as well as some survival time parameters, reliability and hazard rate functions using progressively first-failure censored data. The Bayes estimators are discussed under symmetric and asymmetric loss functions. The use of a discrete prior distribution for parameter 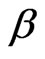 resulted in a closed form expression for the posterior pdf, and the equal probabilities in the discrete distribution cased an element of uncertainly, which can be desirable in some cases. All of the results obtained in this article can be specialized to: a): the firstfailure censored data when
resulted in a closed form expression for the posterior pdf, and the equal probabilities in the discrete distribution cased an element of uncertainly, which can be desirable in some cases. All of the results obtained in this article can be specialized to: a): the firstfailure censored data when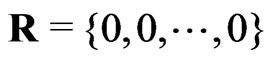 . b): the progressive type II censored order statistics if
. b): the progressive type II censored order statistics if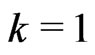 . c): Type II censored order statistics when
. c): Type II censored order statistics when 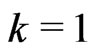 and
and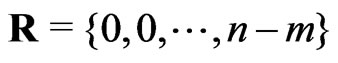 . d): the complete sample case when
. d): the complete sample case when  and
and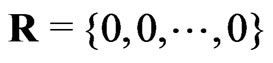 . A simulation study was conducted to examine the performance of the different estimators. From the results, we observe the following:
. A simulation study was conducted to examine the performance of the different estimators. From the results, we observe the following:
• The Bayes estimates are better than the MLEs in general, and the Bayes estimates relative to asymmetric loss functions (LINEX and GE loss) performed better than the others in the sense of comparing the MSE of the estimates. This was true for all censored schemes.
• From all Tables, as the effective sample proportion 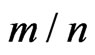 increases, the MSE of the estimators, reduce significantly. Concerning a progressive type-II censoring scheme
increases, the MSE of the estimators, reduce significantly. Concerning a progressive type-II censoring scheme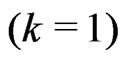 , for a fixed
, for a fixed  and
and , we can determine the censoring scheme
, we can determine the censoring scheme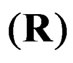 , which is most efficient; for example, in all tables it is seen that the case of scheme II (all items removed at the first failure time point), with
, which is most efficient; for example, in all tables it is seen that the case of scheme II (all items removed at the first failure time point), with  is better than the other cases in the sense of comparing the MSEs.
is better than the other cases in the sense of comparing the MSEs.
• To access the effect of the shape parameters of the asymmetric loss functions  and
and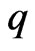 , we examine different values of
, we examine different values of 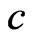 and
and 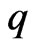 we see that if
we see that if  is near to 0, and
is near to 0, and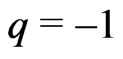 , then the Bayes estimates are almost the same as the estimates under SEL, see Table 3. This is one of the useful properties of working with the asymmetric loss functions.
, then the Bayes estimates are almost the same as the estimates under SEL, see Table 3. This is one of the useful properties of working with the asymmetric loss functions.
• The results establish that for optimum decision making, important should be given on the choice of loss function and not just the choice of prior distribution only.
• The simulation study shows that the MSEs for all estimates are increases as the value of the shape and scale parameters increases.
8. References
[1] R. Viveros and N. Balakrishnan, “Interval Estimation of Parameters of Life from Progressively Censored Data,” Technometrics, Vol. 36, No. 1, 1994, pp. 84-91. doi:10.2307/1269201
[2] N. Balakrishnan and R. A. Sandhu, “A Simple Simulation Algorithm for Generating Progressively Type-II Censored Samples,” The American Statistician, Vol. 49, No. 2, 1995, pp. 229-230. doi:10.2307/2684646
[3] N. Balakrishnan and R. A. Sandhu, “Best Linear Unbiased and Maximum Likelihood Estimation for Exponential Distributions under General Progressive Type-II Censored Samples,” Sankhya: The Indian Journal of Seriestics, Vol. 58, No. 1, 1996, pp. 1-9.
[4] P. Mostert, J. Roux and A. Bekker, “Bayes Estimators of the Life Time Parameters Using the Compound Rayleigh model,” Journal of South African Statistical Association, Vol. 33, No. 2 ,1999, pp. 117-138.
[5] U. Balasooriya and N. Balakrishnan, “Reliability Sampling Plans for Log-Normal Distribution Based on Progressively Censored Samples,” IEEE Transactions on Reliability, Vol. 49, No. 2, 2000, pp. 199-203. doi:10.1109/24.877338
[6] A. Bekker, J. Roux and P. Mostert, “A Generalization of the Compound Rayleigh Distribution: Using a Bayesian Methods on Cancer Survival Times,” Communications in Statistics—Theory and Methods, Vol. 29, No. 7, 2000, pp. 1419-1433. doi:10.1080/03610920008832554
[7] H. K. T. Ng, P. S. Chan and N. Balakrishnan, “Optimal Progressive Censoring Plans for the Weibull Distribution,” Technometrics, Vol. 46, No. 4, 2004, pp. 470-481. doi:10.1198/004017004000000482
[8] H. K. T. Ng, “Parameter estimation for a modifiied Weibull Distribution, for Progressively Type-II Censored Samples,” IEEE Transactions Reliability, Vol. 54, No. 3, 2005, pp. 374-380. doi:10.1109/TR.2005.853036
[9] N. Balakrishnan, N. Kannan, C. T. Lin and H. K. T. Ng, “Point and Interval Estimation for Gaussian Distribution Based on Progressively Type-II Censored Samples,” IEEE Transactions on Reliability, Vol. 52, No. 1, 2003, pp. 90-95. doi:10.1109/TR.2002.805786
[10] A. A. Soliman, “Estimation of Parameters of Life from Progressively Censored Data Using Burr-XII Model,” IEEE Transactions Reliability, Vol. 54, No. 1, 2005, pp. 34-42. doi:10.1109/TR.2004.842528
[11] A. A. Soliman, “Estimation for Pareto Model Using General Progressive Censored Data and Asymmetric Loss,” Communications in Statistics—Theory and Methods, Vol. 37, No. 9, 2008, pp. 1353-1370. doi:10.1080/03610920701825957
[12] D. G. Chen and Y. L. Lio, “Parameter Estimations for Generalized Exponential Distribution under Progressive Type-I Interval Censoring,” Computational Statistics and Data Analysis, Vol. 54, No. 6, 2010, pp. 1581-1591. doi:10.1016/j.csda.2010.01.007
[13] N. Balakrishnan and R. Aggarwala, “Progressive Censoring—Theory, Methods and Applications,” Birkhäuser, Boston, 2000.
[14] N. Balakrishnan, “Progressive Censoring Methodology: An Appraisal,” Test, Vol. 16, No. 2007, pp. 211-289. doi:10.1007/s11749-007-0061-y
[15] L. G. Johnson, “Theory and Technique of Variation Research,” Elsevier, Amsterdam, 1964.
[16] C.-H. Jun, S. Balamurali and S.-H. Lee, “Variables Sampling Plans for Weibull Distributed Lifetimes under Sudden Death Testing,” IEEE Transactions on Reliability, Vol. 55, No. 1, 2006, pp. 53-58. doi:10.1109/TR.2005.863802
[17] J.-W. Wu, W.-L. Hung and C.-H. Tsai, “Estimation of the Parameters of the Gompertz Distribution under the First Failure-Censored Sampling Plan,” Statistics, Vol. 37, No. 6, 2003, pp. 517-525. doi:10.1080/02331880310001598864
[18] J.-W. Wu and H. -Y. Yu, “Statistical Inference about the Shape Parameter of the Burr Type XII Distribution under the Failure-Censored Sampling Plan,” Applied Mathematics and computation, Vol. 163, No. 1, 2005, pp. 443- 482. doi:10.1016/j.amc.2004.02.019
[19] J.-W. Wu, T.-R. Tsai and L.-Y. Ouyang, “Limited Failure-Censored Life Test for the Weibull Distribution,” IEEE Transactions on Reliability, Vol. 50, No. 1, 2001, pp. 107-111. doi:10.1109/24.935024
[20] W.-C. Lee, L.-W. Wu and H.-Y. Yu, “Statistical Inference about the Shape Parameter of the Bathtub-Shaped Distribution under the Failure-Censored Sampling Plan,” International Journal of Information and Management Sciences, Vol. 18, No. 2, 2007, pp. 157-172.
[21] S.-J. Wu and C. Kus, “On Estimation Based on Progressive First Failure-Censored Sampling,” Computational Statistics and Data Analysis, Vol. 53, No. 10, 2009, pp. 1-12.
[22] E. K. AL-Hussaini and Z. F. Jaheen, “Bayes Estimation of the Parameters, Reliability and Failure Rate Functions of the Burr Type XII Failure Model,” Journal of Statistics Computation and Simulation, Vol. 44, 1992, pp. 31-40.
[23] E. K. AL-Hussaini and Z. F. Jaheen, “Approximate Bayes Estimators Applied to the Burr Model,” Communications in Statistics, Vol. 23, 1994, pp. 99-121.
[24] E. K. AL-Hussaini and Z. F. Jaheen, “Bayesian Prediction Bounds for the Burr XII Model,” Communications in Statistics, Vol. 24, 1995, pp. 1829-1842.
[25] E. K. AL-Hussaini and Z. F. Jaheen, “Bayesian Prediction Bounds for the Burr Type XII Distribution in the Presence of Outliers,” Journal of Statistical Planning and Inference, Vol. 55, No. 1, 1996, pp. 23-37. doi:10.1016/0378-3758(95)00184-0
[26] E. K. AL-Hussaini, “Predicting Observables from a General Class of Distributions,” Journal of Statistical Planning and Inference, Vol. 79, No. 1, 1999, pp. 79-91. doi:10.1016/S0378-3758(98)00228-6
[27] N. Balakrishnan and M. Kateri, “Statistical Evidence in Contingency Tables Analysis,” Journal of Statistical Planning and Inference, Vol. 138, No. 4, 2008, pp. 873- 887. doi:10.1016/j.jspi.2007.02.005
[28] H. R. Varian, “A Bayesian Approach to Real State Assessment,” In: E. F. Stephen and A. Zellner, Eds., Studies in Bayesian Econometrics and Statistics in Honor of Leonard J. Savage, North-Holland, Amsterdam, 1975, pp. 195-208.
[29] X. Y. Li, Y. Shi, J. Wei and J. Chai, “Empirical Bayes Estimators of Reliability Performances Using LINEX loss under Progressively Type-II Censored Samples,” Mathematics and Computers in Simulation, Vol. 73, No. 5, 2007, pp. 320-326. doi:10.1016/j.matcom.2006.05.002
[30] G. Prakash and D. C. Singh, “Shrinkage Estimation in Exponential Type-II Censored Data under LINEX Loss,” Journal of the Korean Statistical Society, Vol. 37, No. 1, 2008, pp. 53-61. doi:10.1016/j.jkss.2007.07.002
[31] D. K. Day, M. Ghosh and C. Srinivasan, “Simultaneous Estimation of Parameters under Entropy Loss,” Journal of Statistical Planning and Inference, Vol. 52, 1987, pp. 347-363. doi:10.1016/0378-3758(86)90108-4
[32] D. K. Day and P. L. Liu, “On Comparison of Estimation in Generalized Life Model,” Microelectronics Reliability, Vol. 32, No. 1-2, 1992, pp. 207-221. doi:10.1016/0026-2714(92)90099-7
[33] R. M. Soland, “Bayesian analysis of the Weibull Process with Unknown Scale and Shape Parameters,” IEEE Transactions on Reliability, Vol. 18, No. 4, 1969, pp. 181-184. doi:10.1109/TR.1969.5216348
[34] A. A. Soliman, A. H. Abd Ellah and K. S. Sultan, “Comparison of Estimates Using Record Statistics from Weibull Model: Bayesian and Non-Bayesian Approaches,” Computational Statistics & Data Analysis, Vol. 51, No. 3, 2006, pp. 2065-2077. doi:10.1016/j.csda.2005.12.020
[35] H. F. Martz and R. A. Waller, “Bayesian Reliability Analysis,” Wiley, New York, 1982.
[36] D. M. Stablein, W. H. Carter and J. W. Novak, “Analysis of Survival Data with Non-Proportional Hazard Functions,” Controlled Clinical Trials, Vol. 2, No. 2, 1981, pp. 149-159. doi:10.1016/0197-2456(81)90005-2

