Open Journal of Microphysics
Vol.3 No.2(2013), Article ID:31742,5 pages DOI:10.4236/ojm.2013.32009
A Study on Vibrational Spectra of PH3 and NF3: An Algebraic Approach
1Department of Electronics & Instrumentation Engineering, Lakireddy Bali Reddy College of Engineering, Vijayawada, India
2Department of Physics, KL University, Guntur, India
3Research Scholar, Department of Mathematics, Jawaharlal Nehru Technological University Kakinada, India
4Department of Physics, Miracle Engineering College, Bhogapuram, India
5Department of Electronics & Instrumentation, Rajeev Gandhi Memorial Engineering College, Nandyal, India
6Department of Physics, Lara’s Vignan Institute of Technology and Science, Vadlamudi, India
Email: *srinivasa_karumuri@rediffmail.com
Copyright © 2013 S. R. Karumuri et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 19, 2013; revised April 20, 2013; accepted April 28, 2013
Keywords: Vibrational Spectra; Lie Algebraic Model; Hamiltonian
ABSTRACT
With the new theoretical approach i.e. lie algebraic approach, we have calculated the infrared spectra of Phosphine in the range from 3000 cm−1 to 9500 cm−1 and Nitrogen Trifluoride in the range from 900 cm−1 to 4500 cm−1. The model Hamiltonian, so constructed, seems to describe the P-H and N-F stretching modes accurately with only four numbers of parameters.
1. Introduction
After the recent development of new sophisticated spectroscopic instruments which allows scientists to measure vibrational states of polyatomic molecules with high accuracy and precision. The model is based on the idea of dynamical symmetry, which is expressed through the language of Lie algebras. Applying algebraic techniques, we obtain an effective Hamiltonian operator that conveniently describes the rotational vibrational degrees of freedom of the physical system. The proposed algebraic models are formulated such that they contain the same physical information for both ab initio theories (based on the solution of the Schrödinger equation) and semi empirical approaches (making use of phenomenological expansions in powers of appropriate quantum numbers). Various approaches have been used so far in the study of molecular spectra. Out of these, two important approaches are—1) Dunham expansion [1] and 2) potential approach [2]. A simple analysis of molecular ro-vibrational spectra is provided by the Dunham expansion. This is an expansion of the energy levels in terms of vibrationrotation quantum numbers. Compared to the Dunham expansion, a better analysis is provided by the potential approach in the study of molecular spectra. Energy levels are obtained by solving the Schrödinger equation with an inter-atomic potential. The potential is expanded in terms of interatomic variables. The algebraic models are successful models in the study of the vibrational spectra of small and medium-sized molecules. Some small and large molecules can be studied by using the U(4) and U(2) algebraic models. But, the U(4) model becomes complicated when the number of atoms in a molecule increases more than four. On the other hand, the U(2) model introduced by Wulfman and Levine [3] is found to be successful in explaining the stretching vibrations of polyatomic molecules such as tetrahedral, octahedral, Icosahedral, and benzene-like molecules. The brief review and the research work done with the algebraic models up to the year 2000 and its outlook and perception in the first decade of the 21st century was presented by Iachello and Oss [4-7]. Recently, it is found that Lie algebraic method [8-24] is extremely successful and accurate in calculating the vibrational frequencies of polyatomic molecules compare to the other methods such as Dunham expansion and potential approach method reported earlier. So far no extensive experimental study of the infrared vibrational spectra of Phosphine and Nirogen trifluoride molecules were reported in literatures. As a concrete and complementary technique to the conventional approaches, the algebraic approach has already proven successful in the study of molecular spectra during the last 30 years.
2. Summary of the Algebraic Theory
The model is based on the isomorphism of the U(2) Lie algebra and one dimensional Morse oscillator whose eigen states may be associated with U(2) É O(2) states [25-29]. For a pyramidal molecule, XY3, we introduce three Ui(2) (1 £ i £ 3) algebra to describe X-Y interactions (Figure 1). The possible chains of molecular dynamical groups in pyramidal molecules are (see Equation (1) below)
Which corresponds to local and normal couplings respectively.
The algebraic Hamiltonian in case of stretching mode of pyramidal molecules can be constructed from two chains as
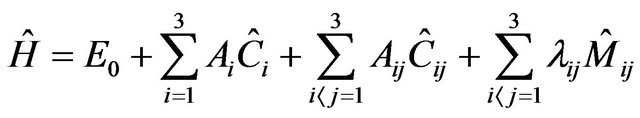 (2)
(2)
In Equation (2), there are three types of contributions. The operators 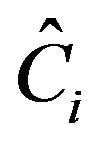 are the Casimir invariant operators of
are the Casimir invariant operators of 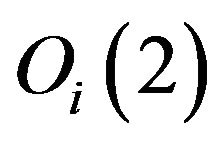 algebras, i = 1, 2, 3. Their diagonal matrix elements in the local basis
algebras, i = 1, 2, 3. Their diagonal matrix elements in the local basis  are of the form
are of the form
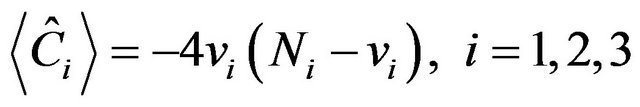 (3)
(3)
with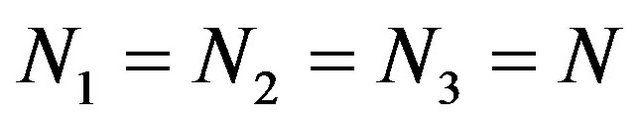 . Interbond couplings can be introduced in terms of operators associated with products of U(2) and O(2) algebras associated different, interacting bonds. The term
. Interbond couplings can be introduced in terms of operators associated with products of U(2) and O(2) algebras associated different, interacting bonds. The term  leads to cross-anharmonicities between pairs of distinct local oscillators which is diagonal with matrix elements given by
leads to cross-anharmonicities between pairs of distinct local oscillators which is diagonal with matrix elements given by
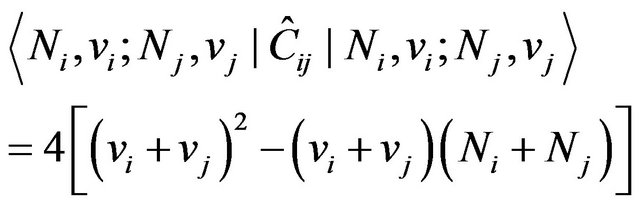 (4)
(4)
The modes of three equivalent X-H bond are now mixed, shifted and split under the action of the operator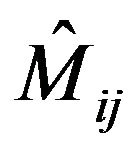 . The Majorana operator is used to describe local mode interactions in pairs and has both diagonal and non-diagonal matrix elements given by (see Equation (5) below)
. The Majorana operator is used to describe local mode interactions in pairs and has both diagonal and non-diagonal matrix elements given by (see Equation (5) below)
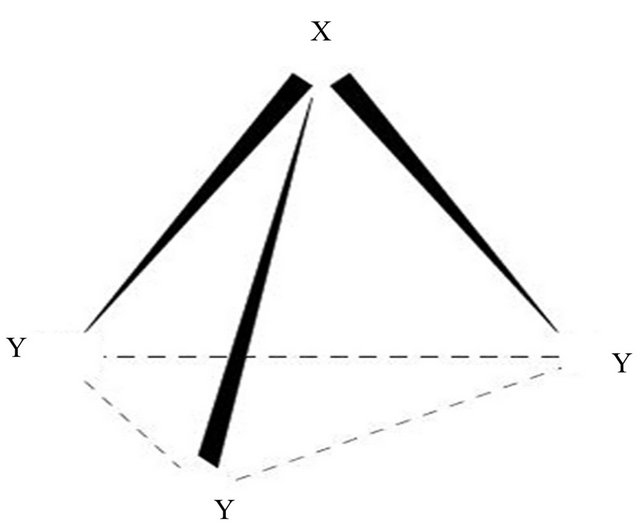
Figure 1. Schematic representation of a pyramidal XY3 molecule.
We shall now construct the local vibrational basis which is given by
 (6)
(6)
The total vibrational quantum number is always conserved for a particular polyad. For a particular XH3 molecule, the stretching bonds 1 to 3 are equivalent. The algebraic Hamilonian depends on 9 linear parameters. These parameters are reduced to only three parameters 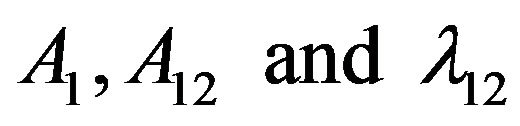 which give the strength of individual and coupling bonds respectively.
which give the strength of individual and coupling bonds respectively.
3. Results and Discussions
Using U(2) algebraic model Vibrational modes of XH3 are computed using algebraic Hamiltonian up to third overtone and are listed in Tables 1 and 2 with fewer algebraic parameters (i.e. A, A12, λ12 and N ).
The vibron number N can be determined by the relation
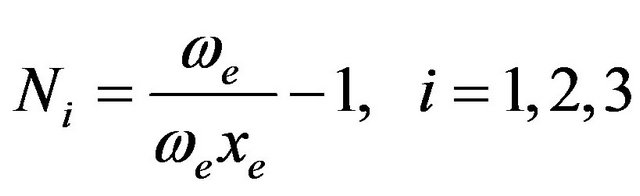 (7)
(7)
where we and wexe are the spectroscopic constants of diatomic molecules [30-33]. The value of N must be as initially guessed from the Equation (7); however one can expect changes in an estimated N, not be larger than ± 20% of the original value. The vibron number N between
|
|
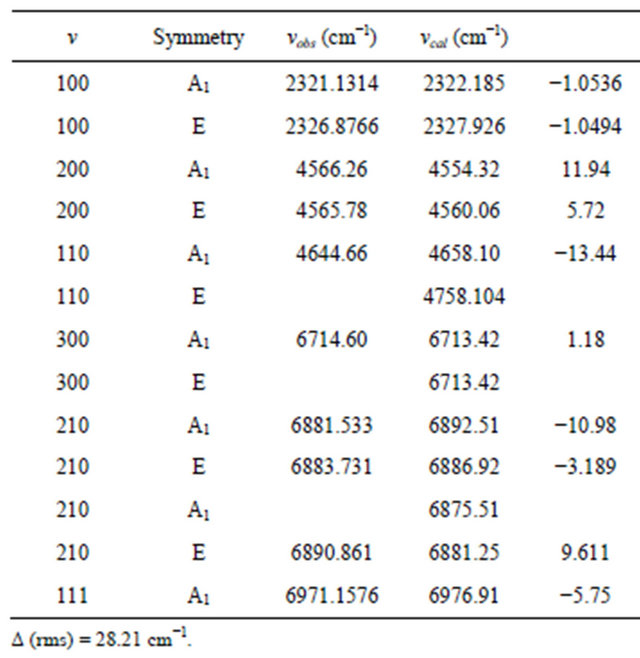
Table 1. Experimental and observed infrared spectra of Phosphine molecule.
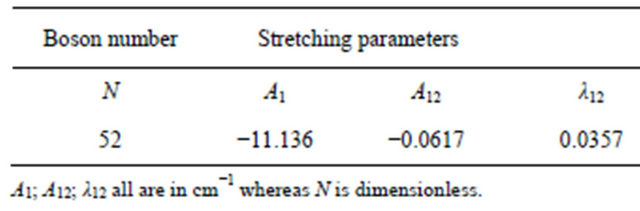
Table 2. Fitting parameters used in the study of Phosphine molecule.
the diatomic molecules As-H and N-H are 68 and 53 respectively. From the Figure 1, it is noticed that some of the bonds are equivalent. It may be noted that during the calculation of the vibrational modes of XH3 molecules, the value of N is kept fixed and not used as free parameter.
The next step is to obtain a guess for the second parameter A. The expression for the single-oscillator fundamental mode is
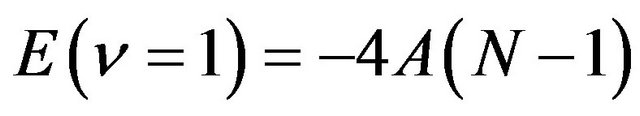 (8)
(8)
In the present case, we have three energies, corresponding to symmetric and antisymmetric combinations of the different local modes. A possible strategy is to use the center of gravity of these modes, so the guess for
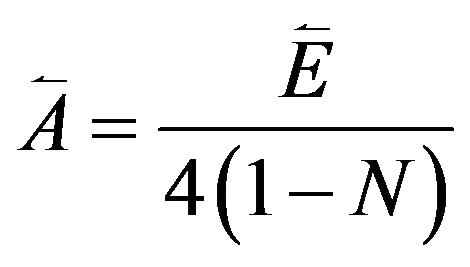 (9)
(9)
The third step is to obtain an initial guess for λ. Its role is to split the initially degenerate local modes, placed here at the common value E used in Equation (8). Such an estimate is obtained by considering the simple matrix structure, we can find
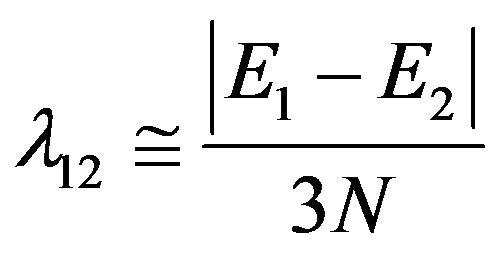 (10)
(10)
With the help of numerical fitting procedure (in a least-square sense) the parameters A and λ12 starting from values Equation (9) and Equation (10), and A12 (whose initial guess can be zero) were adjusted. Vibrational modes of Arsine and Ammonia are computed using algebraic Hamiltonian up to third overtone and are listed in Tables 3 and 4.
4. Conclusion
Using model Hamiltonian, we have presented an algebraic model of one dimensional Morse oscillators which can be used to describe X-H stretching vibrations quite accurately. In third overtones, we have predicted nine (eight) stretching vibrational modes for Arsine (Ammonia) from only one (two) observed data’s. To proceed further it would be necessary to record spectra of higher overtones to produce more accurate vibrational modes. In
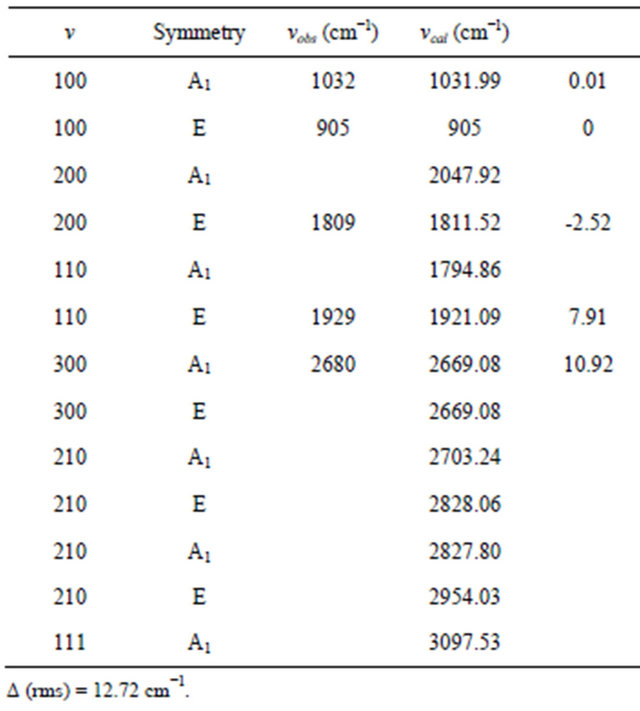
Table 3. Experimental and observed infrared spectra of Nitrogen Trifluoride molecule.
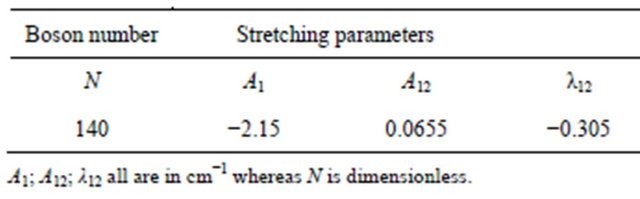
Table 4. Fitting parameters used in the study of Nitrogen Trifluoride molecule.
the last twenty five years, the Lie algebraic approach was found to be successful in explaining vibrational modes of small, medium, polymers, bio-molecules and biopolymers. In view of many possible applications, it is expected that the present calculation will open new windows in the field of spectroscopy.
5. Acknowledgements
The author Dr. Srinivasa Rao Karumuri would like to thank University of Grant Commission (UGC), Govt. of India, New Delhi, India for financial support to carry out the work. The author would like to thank Prof. Stefano Oss for providing the necessary literature for this study.
REFERENCES
- J. L. Dunham, “The Energy Levels of a Rotating Vibrator,” Physical Review Letters, Vol. 41, No. 6, 1932, pp. 721-731. doi:10.1103/PhysRev.41.721
- F. Iachello, “Algebraic Methods for Molecular RotationVibration Spectra,” Chemical Physics Letters, Vol. 78, No. 3, 1981, pp. 581-585. doi:10.1016/0009-2614(81)85262-1
- F. Iachello and R. D. Levine, “Algebraic Approach to Molecular Rotation-Vibration Spectra. I. Diatomic Molecules,” Journal of Chemical Physics, Vol. 77, No. 6, 1982, pp. 3046-3055. doi:10.1063/1.444228
- O. S. van Roosmalen, F. Iachello, R. D. Levine and A. E. L. Dieperink, “Algebraic Approach to Molecular Rotation-Vibration Spectra. II. Triatomic Molecules,” Journal of Chemical Physics, Vol. 79, No. 6, 1983, pp. 2515-2536. doi:10.1063/1.446164
- F. Iachello, S. Oss and R. Lemus, “Vibrational Spectra of Linear Triatomic Molecules in the Vibron Model,” Journal of Molecular Spectroscopy, Vol. 146, No. 1, 1991, pp. 56-78. doi:10.1016/0022-2852(91)90370-P
- O. S. van Roosmalen, I. Benjamin and R. D. Levine, “A Unified Algebraic Model Description for Interacting Vibrational Modes in ABA Molecules,” Journal of Chemical Physics, Vol. 81, No. 12, 1984, pp. 5986-5997. doi:10.1063/1.447600
- F. Iachello and S. Oss, “Overtone Frequencies and Intensities of Bent XY2 Molecules in the Vibron Model,” Journal of Molecular Spectroscopy, Vol. 142, No. 1, 1990, pp. 85-107. doi:10.1016/0022-2852(90)90293-Y
- F. Iachello, S. Oss and R. Lemus, “Linear Four-Atomic Molecules in the Vibron Model,” Journal of Molecular Spectroscopy, Vol. 149, No. 1, 1991, pp. 132-151. doi:10.1016/0022-2852(91)90148-4
- F. Iachello, N. Manini and S. Oss, “Quasi-Linear FourAtomic Molecules in the Vibron Model,” Journal of Molecular Spectroscopy, Vol. 156, No. 1, 1992, pp. 190-200. doi:10.1016/0022-2852(92)90102-T
- F. Iachello, S. Oss and L. Viola, “Vibrational Analysis of Monofluoroacetylene (HCCF) in the Vibron Model,” Molecular Physics, Vol. 78, No. 3, 1992, pp. 545-559. doi:10.1080/00268979300100381
- F. Iachello, S. Oss and L. Viola, “Rotation-Vibration Interaction and Fermi Resonances of HCCF in the Vibron Model,” Molecular Physics, Vol. 78, No. 3, 1993, pp. 561- 575. doi:10.1080/00268979300100391
- R. Lemus and A. Frank, “Algebraic Approach to Vibrational Spectra of Tetrahedral Molecules: Application to Methane,” Journal of Chemical Physics, Vol. 101, No. 10, 1994, pp. 8321-8332. doi:10.1063/1.468450
- F. Iachello and S. Oss, “Vibrational Modesoof Polyatomic Molecules in the Vibron Model,” Journal of Molecular Spectroscopy, Vol. 153, No. 1-2, 1992, pp. 225- 239. doi:10.1016/0022-2852(92)90471-Y
- F. Iachello and S. Oss, “Algebraic Model of Bending Vibrations of Complex Molecules,” Chemical Physics Letters, Vol. 205, No. 2-3, 1993, pp. 285-289. doi:10.1016/0009-2614(93)89244-C
- F. Iachello and S. Oss, “Model of n Coupled Anharmonic Oscillators and Applications to Octahedral Molecules,” Physical Review Letters, Vol. 66, No. 23, 1991, pp. 2976- 2979. doi:10.1103/PhysRevLett.66.2976
- F. Iachello and S. Oss, The European Physical Journal D, Vol. 19, 2002, p. 307.
- F. Iachello and R. D. Levine, “Algebraic Theory of Molecules,” Oxford University Press, New York, 1995.
- A. Frank and V. P. van Isacker, “Algebraic Methods in Molecular and Nuclear Structure Physics,” Wiley, New York, 1994.
- S. Oss, “Algebraic Models in Molecular Spectroscopy,” Advances in Chemical Physics, Vol. 93, 1966, p. 455. doi:10.1002/9780470141526.ch8
- N. K. Sarkar, J. Choudhury and R. Bhattacharjee, “An Algebraic Approach to the Study of the Vibrational Spectra of HCN,” Molecular Physics, Vol. 104, No. 9, 2006, p. 3051-3055. doi:10.1080/00268970600954235
- N. K. Sarkar, J. Choudhury and R. Bhattacharjee, Indian Journal of Physics, Vol. 82, No. 6, 2008, pp. 767.
- N. K. Sarkar, J. Choudhury, S. R. Karumuri and R. Bhattacharjee, “An Algebraic Approach to the Comparative Study of the Vibrational Spectra of Monofluoroacetylene (HCCF) and Deuterated Acetylene (HCCD),” Molecular Physics, Vol. 106, No. 5, 2008, pp. 693-702. doi:10.1080/00268970801939019
- J. Choudhury, S. R. Karumuri, N. K. Sarkar and R. Bhattacharjee, “Vibrational Spectroscopy of SnBr4 and CCl4 Using Lie Algebraic Approach,” Pramana, Vol. 71, No. 3, 2008, pp. 439-445. doi:10.1007/s12043-008-0123-z
- J. Choudhury, N. K. Sarkar and R. Bhattacharjee, Indian Journal of Physics, Vol. 82, No. 5, 2008, p. 561.
- S. R. Karumuri, N. K. Sarkar, J. Choudhury and R. Bhattacharjee, “Vibrational Spectroscopy of Cm-H, Cβ-Cβ Stretching Vibrations of Nickel Metalloporphyrins: An Algebraic Approach,” Molecular Physics, Vol. 106, No. 14, 2008, pp. 1733-1737. doi:10.1080/00268970802248998
- S. R. Karumuri, J. Choudhury, N. K. Sarkar and R. Bhattacharjee, Journal of Environmental Research and Development (JERAD), Vol. 3, No. 1, 2008, p. 250.
- S. R. Karumuri, J. Choudhury, N. K. Sarkar and R. Bhattacharjee, “Vibrational Spectra of Nickel Metalloporphyrins: An Algebraic Approach,” Pramana, Vol. 72, No. 3, 2009, pp. 517-525. doi:10.1007/s12043-009-0046-3
- S. R. Karumuri, N. K. Sarkar, J. Choudhury and R. Bhattacharjee, Journal of Molecular Spectroscopy, Vol. 255, No. 2, 2009, pp. 183-188. doi:10.1016/j.jms.2009.03.014
- S. R. Karumuri, J. Choudhury, N. K. Sarkar and R. Bhattacharje, “Vibrational Spectroscopy of Cm-C/Cb-Cb Stretching Vibrations of Copper Tetramesityl Porphyrin: An Algebraic Approach,” Pramana, Vol. 74, No. 1, 2010, pp. 57-66. doi:10.1007/s12043-010-0007-x
- J. Choudhury, N. K. Sarkar, S. R. Karumuri and R. Bhattacharjee, “Vibrational Spectroscopy of CH/CD Stretches in Propadiene: An Algebraic Approach,” Chinese Physics Letters, Vol. 26, No. 2, 2009, Article ID: 020308. doi:10.1088/0256-307X/26/2/020308
- N. K. Sarkar, J. Choudhury, S. R. Karumuri and R. Bhattacharjee, The European Physical Journal D, Vol. 53, 2009, p. 163.
- J. Choudhury, S. R. Karumuri, N. K. Sarkar and R. Bhattacharjee, “Vibrational Spectrum of CF4 Isotopes in an Algebraic Model,” Pramana, Vol. 73, No. 5, 2009, pp. 881-887. doi:10.1007/s12043-009-0155-z
- L. Halonen, “Local Mode Vibrations in Polyatomic Molecules,” Advances in Chemical Physics, Vol. 104, 1998, p. 41. doi:10.1002/9780470141632.ch2
NOTES
*Corresponding author.



