Open Journal of Geology
Vol.06 No.09(2016), Article ID:70469,10 pages
10.4236/ojg.2016.69078
M5 Model Tree to Predict Temporal Evolution of Clear-Water Abutment Scour
R. Biabani1, M. Meftah Halaghi2, Kh. Ghorbani2
1Department of Water Engineering, Faculty of Agriculture, Tabriz University, Tabriz, Iran
2Department of Water Engineering, Gorgan University of Agricultural Sciences and Natural Resources, Gorgan, Iran

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 15, 2016; Accepted: September 6, 2016; Published: September 9, 2016
ABSTRACT
Scour is a natural phenomenon that is created by the rivers streams or the flood which brings about transferring or eroding of bed materials. To have accurate and safe erosion control structures design, maximum scour depth in downstream of the structures gains specific significance. In the current study, M5 model tree as remedy data mining approaches is suggested to estimate the scour depth around the abutments. To do this, Kayaturk laboratory data (2005), with different hydraulic conditions, are used. Then, the results of M5 model were also compared with genetic programming (GP) and pervious empirical results to investigate the applicability, ability, and accuracy of these procedures. To examine the accuracy of the results yielded from the M5 and GP procedures, two performance indicators (determination coefficient (R2) and root mean square error (RMSE)) were used. The comparison test of results clearly shows that the implementation of M5 technique sounds satisfactory regarding the performance indicators (R2 = 0.944 and RMSE = 0.126) with less deviation from the numerical values. In addition, M5 tree model, by presenting relationships based on liner regression, has good capability to estimate the depth of scour abutment for engineers in practical terms.
Keywords:
Abutments, Scour Depth, M5 Model Tree, Genetic Programming Model (GP)

1. Introduction
Scour is the result of water erosion that causes digging and transferring bed materials and rivers banks. Bridge collapse, due to the total scour in foundation (including abutment and pier), makes the significance of the study about scour prediction and different countermeasures against it completely clear. According to Melville [1] , among 108 bridge collapse that happened between1960-1984 in Newslands, 29 of them were related to scour bridge abutment. Also, 70 percent of bridge collapse expenditure in Newlands was due to this matter. Data show that scour bridge abutment is a serious problem. Studies carried out on 383 bridges in the United State show that 25% of pier destructions and 72% of abutment destructions have been the cause of bridge collapse.
Due to lack of enough information in this issue, studies related to scour pattern began from early 1980 (e.g., at Auckland University). Richardson and Richardson [2] showed that the presented relations estimate the scour amount in abutment more than the real amount. One probable reason is that obtained relations of the extracted results are from rectangular channels; while a natural river mostly consists of compound channels with main channel and flood plains. The other reason for the inaccuracy of the presented data is the lack of attention to scour time development. That is why in recent decades several studies have been conducted in this field and researchers presented some relations for scour time development, such as Gill [3] , Cunha [4] , Cardoso and Bettes [5] , Kothyari and Ranga Raju [6] , Ballio and Orsi [7] , Radice et al. [8] , Oliveto and Hager [9] , Coleman et al. [10] .
The exact estimation of scour depth by the help of laboratory studies is a difficult, costly and time-consuming task. Hence, by developing computer software and using in hydraulic research, the estimation of scour depth has been carried out applying these methods by researchers.
Genetic Programming is one of these techniques that are being used in water engineering in recent decades. Azamathulla et al. [11] [12] have used linear genetic programming for determining pipe line scour. Also, the longitudinal dispersion coefficient in streams was determined by Azmathulla and Ghani [13] .
Salmasi et al. [14] estimated friction factors in pipes (f) according to changes in Reynolds number and relative roughness by the use of genetic programming and artificial neural networks. Guven and Gunal [15] used genetic algorithm to determine the depth of downstream water structure and compared the obtained results with empirical results of researchers.
Recently a new method called M5 decision tree model is presented for solving various problems and predicting output parameters. This model is used to solve engineering problems such as rainfall-runoff modeling [16] , flood forcasting [17] , water level discharge relationship [18] , sedimentation amount measurement in river [19] , sedimentation modeling [20] , suspended sediment load [21] , evaporation aspiration measurement [22] , scour depth measurement around bridge piers [22] , significant wave height prediction [23] and flow discharge prediction in compound channels [24] . In this method, based on the most important input variables, data are divided into different separated groups and for each group a multivariate liner regression equation is presented in order to measure output variable. Simple measurement, accurate results and the generalizability of the results are the great profitable outcomes of this model.
The purpose of this study is to estimate time development of scour around abutments by the use of M5 and GP liner regression technique. The comparison of the obtained results with the empirical results shows the high capability of this software to estimate time development of scour depth.
2. M5 Model Tree
The following idea is used by this machine-learning technique: the parameter space is split into areas (subspaces) and in each of them a linear regression model is built. As a matter of fact, the resulting model would be regarded as a modular model, or a committee machine, in which the linear models being specialized on the particular subsets of the input space.
The algorithm called the M5 algorithm is utilized for the sake of inducing a model tree [25] . A collection K of training examples is taken into account. Each example is characterized by the values of a fixed set of (input) attributes and has an associated target (output) value. The main objective is to construct a model that relates a target value of the training cases to the values of their input attributes. The quality of the model will be generally accurately estimated as if it anticipates the target values of the cases which are unseen.
A divide-and-conquer method constructs Tree-based models. The set K is either related to a leaf, or some tests are chosen to split K into subsets corresponding to the test outcomes and a similar procedure is applied recursively to the subsets. The splitting criterion used for M5 model tree algorithm depends on treating the standard deviation of the class values that reach a node as a measure of the error at that node, and calculating the expected reduction in this error as a result of testing each attribute at that node. To compute the standard deviation reduction (SDR), the help of this formula seems necessary:
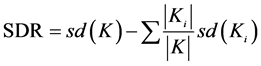 (1)
(1)
where K indicates a set of examples that reaches the node; K shows the subset of examples that have the ith outcome of the potential set; and sd stands for the standard deviation.
After examining all potential splits, M5 selects the item that enhances the expected error reduction fully. Splitting in M5 ceases when the class values of all the instances that reach a node differ just marginally, or only a few instances are left. The relentless division often creates over-elaborate structures that must be pruned back, namely by substituting a subtree with a leaf. Eventually, a smoothing process is carried out with the aim of compensating for the sharp discontinuities that will unavoidably take place between adjacent linear models at the leaves of the pruned tree, especially for some models constructed from a smaller number of training examples. In this process, the adjacent linear equations are updated in such a way that the projected outputs for the neighboring input vectors corresponding to the different equations are becoming close in terms of value. For more details of this process, Quinlan [25] and Witten & Frank [26] can be referred to.
3. Genetic Programming
Genetic programming, a branch of the genetic algorithm, is a method for acquiring the most “fit” computer programs by taking the full advantage of artificial evolution [27] . The GP optimizes not only the coefficients but also constants in a function and the function type itself. A possible function is determined by given mathematical operators, such as +, −, ×, sin, expand so forth. Each function indirectly includes an assignment to a variable, which paves the way for the use of multiple program outputs in GP; nevertheless, in tree-based GP those side effects need to be integrated explicitly. The GP encodes a function as a tree with nodes and branches, and then optimizes functions according to natural principles. The GP procedure bears some resemblances to a genetic algorithm, which generates solutions as a parent population, and then fortifies solutions by selection, crossover, and mutation processes [28] .
The great merit of GP for the modeling process lies in its ability to produce models that construct an understandable structure, i.e., a formula or equation. Accordingly, for “data rich, theory poor” instances, GP benefits may outweigh other techniques inasmuch as GP can self-modify, via the genetic loop, a population of function trees so as to ultimately produce an “optimal” and physically interpretable model [29] .
The following expression can analyze the fitness of GP algorithm:
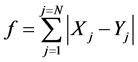 (2)
(2)
where Xj = value returned by a chromosome for the fitness case j and Yj = expected value for the fitness case j. This configuration has been tested for the proposed GP model and has been found adequate [11] [12] .
4. Dimensional Analysis
Kayatork [30] laboratory measurements, which investigated the effect of abutment height on scour time development, have been considered as software input data. These tests had been carried out in a rectangular channel with the height of 0.3 meters and the weight of 1.5 meters for investigating the effect of four different heights of abutment on scour time development. For clear-water approach flow conditions, the maximum scour depth at an abutment is a function of the following parameters:
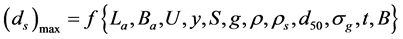 (3)
(3)
where, La = abutment length, Ba = abutment width, U = mean approach flow velocity, y = flow depth, S = slope of the channel, g = gravitational acceleration, ρ = density of the fluid, ρs = density of the sediment, µ = dynamic viscosity of fluid, d50 = median particle grain size, σg = geometric standard deviation of sediment size distribution, t = time variation of scour when it starts, B = width of channel (Figure 1). In terms of dimensionless parameters Equation (3) can be written as:
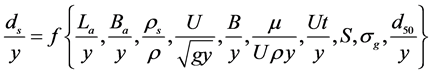 (4)
(4)
Figure 1. Definition sketch of abutment arrangement.
In this study, channel bed sloop, channel width, sediment particle size, flow depth, and consequently Froude number assumed constant. Finally, the above dimensional analysis is summarized as follows:
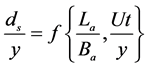 (5)
(5)
The first dimensionless relation shows the geometry of the model and represents the fraction of height to weight, and the second dimensionless number is time dimensionless parameter.
Summary
In this study statistical parameters of correlation coefficient (R2) and root mean square error (RMSE) were used in order to compare the results of two regression methods. The lesser amount of RMSE (0.01) and the larger amount of correlation coefficient (0.0961) introduced GP model better in predicting scour time development in abutments (Table 1). As it was aforementioned about regression model structures, the dependent variable was estimated by breaking computing space into subspaces and presenting liner regression for each subspace and thus computational error increase.
Figure 2 provides the graph plotted between actual and predicted value of scour depth obtained by using M5 model tree. This figure suggests that about 91% of the predicted values lie inside the ±25% lines. Predicted amount versus actual results diagram of time scour depth related to Genetic programming model shows that 93% of data lie within 25% allowed error range (Figure 3).
One major advantage of M5 model tree is the availability of three simple linear relations (Equations (9), (10) and (11)) which can be easily used to predict the scour around the abutments (Figure 4).
Figure 2. Actual vs. Predicted Scour using M5 Model.
Figure 3. Actual vs. Predicted Scour using GP Model.
Figure 4. The acquired tree structure from M5 to measurement the momentary scour depth in abutments.
Table 1. Correlation coefficient and root mean square error for M5 Model Tree and Genetic programming.
The temporal variation of local scour depth can be defined as a function of its independent parameters when dimensionless abutment height (La/Ba) is less than 1.12 by the following expressions:
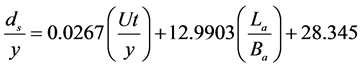 (6)
(6)
On the other hand, if dimensionless abutment height is greater than 1.12, temporal variation of local scour depth is broken into two parts (Equations (7) and (8))
If time dimensionless parameter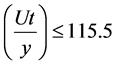 :
:
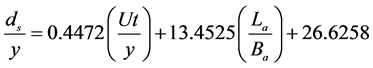 (7)
(7)
And for 
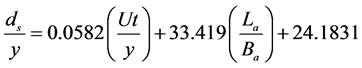 (8)
(8)
The scour development process aroundthe abutment for different heights was shows in Figure 5. For the cases with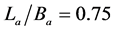 , abutments have no significant effect on flow pattern, therefore equilibrium scour depth and time to reach the equilibrium scour depth decrease and this matter was presented by decision tree model in Equation (6). With increasing abutment height, time development of local scour depth changed rapidly when the time dimensionless parameter is less than 115.5 and after the certain time the depth of scour gradually remains. So, M5 model shows this procedure well by breaking the data into two series.
, abutments have no significant effect on flow pattern, therefore equilibrium scour depth and time to reach the equilibrium scour depth decrease and this matter was presented by decision tree model in Equation (6). With increasing abutment height, time development of local scour depth changed rapidly when the time dimensionless parameter is less than 115.5 and after the certain time the depth of scour gradually remains. So, M5 model shows this procedure well by breaking the data into two series.
Non-liner regression relation is represented by Genetic Programming model as follows:
 (9)
(9)
In contrast with the M5 model results, Genetic Programming model trained by dimensionless data was complicated, thus the regression tree has adaptability and capability to predict the scour depth around the abutments.
Figure 6 represents the comparison between the data reported by Cardoso and Bettes [5] and Coleman et al. [10] and those of the present work for the M5 model tree. As can be seen, M5 model predict the scour depth more accurately than empirical relations.
5. Conclusion
The potential of M5 model tree in predicting the temporal local scour depth around the abutments was investigated in this paper by using Kayaturk laboratory data [30] . A
Figure 5. Time development of scour depth for different length of abutment.
Figure 6. Actual vs. Predicted Scour using Four Empirical Relations.
major conclusion from this study is that M5 model tree works equally well to the Genetic Programming model and provides improved results in comparison to all three empirical relations used in this study. Furthermore, M5 decision tree model, besides simple calculation and equations, has good capability in estimating the depth of time scour in abutment.
Cite this paper
Biabani, R., Meftah Halaghi, M. and Ghorbani, Kh. (2016) M5 Model Tree to Predict Temporal Evolution of Clear-Water Abutment Scour. Open Journal of Geology, 6, 1045-1054. http://dx.doi.org/10.4236/ojg.2016.69078
References
- 1. Melville, B.W. (1992) Local Scour at Bridge Abutments. Journal of Hydraulic Engineering, 118, 615-631.
http://dx.doi.org/10.1061/(ASCE)0733-9429(1992)118:4(615) - 2. Reddy, M.J. and Ghimire, B.N.S. (2009) Use of Model Tree and Gene Expression Programming to Predict the Suspended Sediment Load in Rivers. Journal of Intelligent Systems, 18, 211-227.
- 3. Pal, M. and Deswal, S. (2009) M5 Model Tree Based Modelling of Reference Evapotranspiration. Hydrologic Processes, 30, 1437-1443.
http://dx.doi.org/10.1002/hyp.7266 - 4. Etemad Shahidi, A. and Mahjoobi, J. (2009) Comparison between M5 Model Tree and Neural Networks for Prediction of Significant Wave Height in Lake Superior. Ocean Engineering, 36, 1175-1181.
http://dx.doi.org/10.1016/j.oceaneng.2009.08.008 - 5. Zahiri, A. and Azamathulla, H. (2014) Comparison between Linear Genetic Programming and M5 Tree Models to Predict Flow Discharge in Compound Channels. Journal of Neural Computing and Applications, 24, 413-420.
http://dx.doi.org/10.1007/s00521-012-1247-0 - 6. Quinlan, J.R. (1992) Learning with Continuous Classes. Proceedings of Australian Joint Conference on Artificial Intelligence, Hobart 16-18 November 1992, 343-348.
- 7. Witten, I.H. and Frank, E. (2005) Data Mining: Practical Machine Learning Tools and Techniques with Java Implementations. Morgan Kaufmann, San Francisco.
- 8. Johari, A., Habibagahi, G. and Ghahramani, A. (2006) Prediction of Soil-Water Characteristic Curve Using Genetic Programming. Journal of Geotechnical and Geoenvironmental Engineering, 132, 661-665.
http://dx.doi.org/10.1061/(ASCE)1090-0241(2006)132:5(661) - 9. Koza, J.R. (1992) Genetic Programming: On the Programming of Computers by Means of Natural Selection. MIT, Mass.
- 10. Muttil, N. and Chau, K.W. (2006) Neural Network and Genetic Programming for Modeling Coastal Algal Blooms. International Journal of Environment and Pollution, 28, 223-238.
http://dx.doi.org/10.1504/IJEP.2006.011208 - 11. Kayaturk, S.Y. (2005) Scour and Scour Protection at Bridge Abutments. PhD. Thesis on Civil Engineering, Natural and Applied Sciences, Middle East Technical University, Ankara, 213 p.
- 12. Bhattacharya, B., Price, R.K. and Solomatine, D.P. (2007) Machine Learning Approach to Modeling Sediment Transport. Journal of Hydraulic Engineering, 133, 440-450.
http://dx.doi.org/10.1061/(ASCE)0733-9429(2007)133:4(440) - 13. Bhattacharya, B. and Solomatine, D.P. (2006) Machine Learning in Sedimentation Modelling. Neural Networks, 19, 208-214.
http://dx.doi.org/10.1016/j.neunet.2006.01.007 - 14. Bhattacharya, B. and Solomatine, D.P. (2005) Neural Networks and M5 Model Trees in Modeling Water Level-Discharge Relationship. Neurocomputing, 63, 381-396.
http://dx.doi.org/10.1016/j.neucom.2004.04.016 - 15. Solomatine, D.P. and Xue, Y. (2004) M5 Model Trees and Neural Networks: Application to Flood Forecasting in the Upper Reach of the Huai River in China. Journal of Hydraulic Engineering, 6, 491-501.
http://dx.doi.org/10.1061/(asce)1084-0699(2004)9:6(491) - 16. Solomatine, D.P. and Dulal, K. (2003) Model Tree as an Alternative to Neural Network in Rainfall-Runoff Modeling. Hydrological Sciences Journal, 48, 399-411.
http://dx.doi.org/10.1623/hysj.48.3.399.45291 - 17. Guven, A. and Gunal, M. (2008) Prediction of Scour Downstream of Grade-Control Structures Using Neural Networks. Journal of Hydraulic Engineering, 134, 1656-1660.
http://dx.doi.org/10.1061/(ASCE)0733-9429(2008)134:11(1656) - 18. Salmasi, F., Khatibi, R. and Ghorbani, M.A. (2011) A Study of Friction Factor Formulation in Pipes Using Artificial Intelligence Techniques and Explicit Equations. Turkish Journal of Engineering and Environmental Sciences, 35, 1-18.
- 19. Azmathulla, H.M. and Ghani, A. (2009) Genetic Programming for Longitudinal Dispersion Coefficients in Streams. Water Resources Management, 25, 1537-1544.
http://dx.doi.org/10.1007/s11269-010-9759-9 - 20. Azamathulla, H.M., Ghani, A.A., Zakaria, N.A. and Guve, A. (2010) Genetic Programming to Predict Bridge Pier Scour. Journal of Hydraulic Engineering, 136, 165-169.
http://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000133 - 21. Azamathulla, H.M., Guven, A. and Demir, Y.K. (2008) Linear Genetic Programming to Scour below Submerged Pipeline. Ocean Engineering, 38, 995-1000.
- 22. Coleman, S.E., Lauchlan, C.S. and Melville, B.W. (2003) Clear-Water Scour Development at Bridge Abutments. Journal of Hydraulic Research, 41, 521-531.
http://dx.doi.org/10.1080/00221680309499997 - 23. Oliveto, G. and Hager, W.H. (2002) Temporal Evolution of Clear-Water Pier and Abutments Scour. Journal of Hydraulic Engineering, 128, 811-820.
http://dx.doi.org/10.1061/(ASCE)0733-9429(2002)128:9(811) - 24. Radice, A., Franzetti, S. and Ballio, F. (2002) Local Scour at Bridge Abutments. International Conference on Fluvial Hydraulics, River Flow, 2, 1059-1068.
- 25. Ballio, F. and Orsi, E. (2001) Time Evolution of Scour around Bridge Abutments. Water Engineering Research, 2, 243-259.
- 26. Kothyari, U.C. and Ranga Raju, K.G. (2001) Scour around Spur Dikes and Bridge Abutments. Journal of Hydraulic Engineering, 39, 367-374.
http://dx.doi.org/10.1080/00221680109499841 - 27. Cardoso, A.H. and Bettess, R. (1999) Effects of Time and Channel Geometry on Scour at Bridge Abutments. Journal of Hydraulic Engineering, 125, 388-398.
http://dx.doi.org/10.1061/(ASCE)0733-9429(1999)125:4(388) - 28. Cunha, L.V. (1975) Time Evolution of Local Scour. The 16th IAHR Congress Proceedings, Sao Paulo.
- 29. Gill, M.A. (1972) Erosion of Sand Beds around Spur Dikes. Journal of the Hydraulics Division, 98, 1587-1602.
- 30. Richardson, J.R. and Richardson, E.V. (1994) Practical Method for Scour Prediction at Bridge Piers. Proceeding of ASCE National Conference on Hydraulic Engineering, Buffalo, 1-5.








