Received 27 March 2016; accepted 15 July 2016; published 18 July 2016

ABSTRACT

A proper edge t-coloring of a graph G is a coloring of its edges with colors 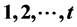such that all colors are used, and no two adjacent edges receive the same color. A cyclically interval t-coloring of a graph G is a proper edge t-coloring of G such that for each vertex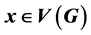, either the set of colors used on edges incident to x or the set of colors not used on edges incident to x forms an interval of integers. In this paper, we provide a new proof of the result on the colors in cyclically interval edge colorings of simple cycles which was first proved by Rafayel R. Kamalian in the paper “On a Number of Colors in Cyclically Interval Edge Colorings of Simple Cycles, Open Journal of Discrete Mathematics, 2013, 43-48”.

Keywords:

Edge Coloring, Interval Edge Coloring, Cyclically Interval Edge Coloring

1. Introduction

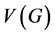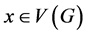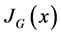All graphs considered in this paper are finite undirected simple graphs. For a graph G, let and denote the sets of vertices and edges of G, respectively. For a vertex, let and 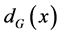denote the subset of 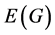incident with the vertex x, and the degree of the vertex x in G, respectively. We denote the maximum degree of vertices of G. A simple path with 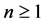edges is denoted by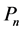. A simple cycle with edges is denoted by.

For an arbitrary finite set A, we denote by 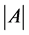the number of elements of A. The set of positive integers is denoted by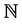. An arbitrary nonempty subset of consecutive integers is called an interval. An interval with the minimum element p and the maximum element q is denoted by. We denote and the sets of even and odd integers in, respectively. An interval D is called a h-interval if.

A function is called a proper edge t-coloring of a graph G, if all colors are used, and no two adjacent edges receive the same color. The minimum value of t for which there exists a proper edge t-coloring of a graph G is denoted by. If, and is a proper edge t-coloring of a graph G, then let. A proper edge t-coloring of a graph G is called an interval t-coloring of G if for any, the set is a -interval. A graph G is interval colorable if it has an interval t-coloring for some positive integer t. The concept of interval edge coloring of graphs was introduced by Asratian and Kamalian [1] . In [1] [2] , the authors showed that if G is interval colorable, then.

For any, we denote by the set of graphs for which there exists an interval t-coloring. Let

. For any graph, the minimum and the maximum values of t for which G has an interval

t-coloring are denoted by and, respectively. For a graph, let.

A proper edge t-coloring a of a graph G is called a interval cyclic t-coloring of G, if for any, at least one of the following two conditions holds:

1) is a -interval,

2) is a -interval.

A graph G is interval cyclically colorable if it has a cyclically interval t-coloring for some positive integer t. This type of edge coloring under the name of “p-coloring” was first considered by Kotzig [3] , and the concept of cyclically interval edge coloring of graphs was explicitly introduced by de Werra and Solot [4] .

For any, we denote by the set of graphs for which there exists a interval cyclic t-coloring. Let

. For any graph, the minimum and the maximum values of t for which G has a cyclically

interval t-coloring are denoted by and respectively. For a graph, let

.

It is clear that for any, and. Note that for an arbitrary graph G,. It is also clear that for any, the following inequality is true:

Let T be a tree. Kamalian [5] [6] showed that, was an interval, and provided the exact values of the parameters and. Kamalian [7] [8] also proved that. Some interesting results on cyclically interval t-colorings and related topics were obtained in [3] [4] [9] - [14] . For any integer, Kamalian [13] proved that, determined the set, and provided the following theorem.

Theorem 1 (R. R. Kamalian [13] ) For any integers and, if and only if

In this paper, we provide a new proof of the theorem. The terms and concepts that we do not define can be found in [15] .

2. Main Result

Proof of Theorem 1. Suppose that, in clockwise order along the cycle, the vertices of are and the edges of are, where for, and. Since and

We know that if or

then.

First we prove that if and

then.

Case 1. n is odd.

For any, let

It is easy to check that is a cyclically interval t-coloring of.

Case 2. n is even.

For any, let

If is odd, then let

For any, let

It is easy to check that, in each case, is a cyclically interval t-coloring of.

Now let us prove that if, and, then

By contradiction. Suppose that there are, , and

such that has a cyclically interval -coloring.

Case 1. is odd.

Clearly,. Let and be two edges of such that and. Without loss of generality, we may assume. Let be the subgraph induced by, and

be the subgraph induced by, respectively. Since is even and is a cyclically interval

-coloring of, then and are all even. So we have that is even, a contradiction.

Case 2. is even.

Let H be the graph removing from the graph the edges with the colors except 1 and, and the graph removing from the graph H all its isolated vertices.

Case 2.1. is connected.

Let F be the subgraph of induced by, where and are the two pendant edges of.

Clearly,. If is odd, then. Since is a cyclically interval -

coloring of, then is a interval -coloring with. So we have

, a contradiction.

If is even, then. Since is a cyclically interval -coloring of, then is a interval -coloring. So we know that is odd, and then is odd, a con- tradiction.

Case 2.2. is a graph with m connected components,.

Suppose that, in clockwise order along the cycle, the m connected components of are. Without loss of generality, we may also assume that and.

Clearly, and. Let,

and. Let be the subgraph induced by,

and L₄ be the subgraph induced by, respectively. Let or,

say. Since is a cyclically interval -coloring of, then is a interval -

coloring with. So we have, a contradiction.

Now let and. Since is a cyclically interval -coloring of, then

and are all interval -coloring. So we have, a con-

tradiction. □

Acknowledgements

We thank the editor and the referee for their valuable comments. Research of Y. Zhao is funded in part by the Natural Science Foundation of Hebei Province of China under Grant No. A2015106045, and in part by the Institute of Applied Mathematics of Shijiazhuang University.

Cite this paper

Nannan Wang,Yongqiang Zhao, (2016) Note on Cyclically Interval Edge Colorings of Simple Cycles. Open Journal of Discrete Mathematics,06,180-184. doi: 10.4236/ojdm.2016.63016

References

NOTES

^*Corresponding author.