ABSTRACT

In this paper, we extend the definition of Boolean canalyzing functions to the canalyzing functions of multi-state case. Namely, 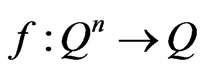, where. We obtain its cardinality and the cardinalities of its various subsets (They may not be disjoint). When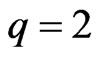, we obtain a combinatorial identity by equating our result to the formula in [1]. For a better understanding to the magnitude, we obtain the asymptotes for all the cardinalities as eithe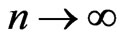r or.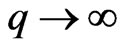

1. Introduction

The idea of canalization was initiated from Waddington, C. H. [2]. When comparing the class of canalyzing functions to other classes of functions with respect to their evolutionary plausibility as emergent control rules in genetic regulatory systems, it is informative to know the number of canalyzing functions with a given number of input variables [1]. However, the Boolean network modeling paradigm is rather restrictive, with its limit to two possible functional levels, ON and OFF, for genes, proteins, etc. Many discrete models of biological networks therefore allow variables to take on multiple states. Common used discrete multi-state model types are socalled logical models [3], Petri nets [4], and agentbased models [5].

In this paper, we generalize the concept of Boolean canalyzing rules to the multi-state case. By generalizing the results in [1], we provide formulas for the cardinalities of various subsets of canalyzing functions. We also obtain the asymptotes of these cardinalities as eithe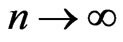r or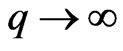. We obtain a combinatorial identity by equating our result to the formula in [1].

2. Preliminaries

In this section we introduce the definition of a canalyzing function.

Let 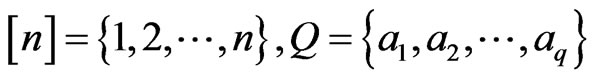and .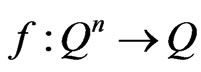

A function is canalyzing if there is a variable 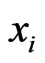and an element so that the value of the function is fixed once variable 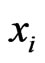is fixed at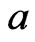. More precisely, we have the following definitions.

Definition 2.1

1) The function 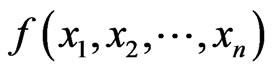is 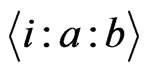canalyzing if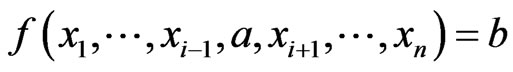, for all .

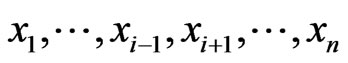2) The function 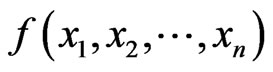is 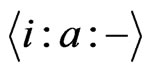canalyzing if there exists 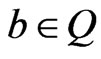such that 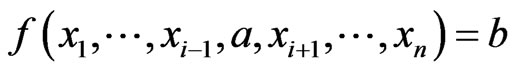, for all .

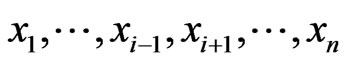3) The function 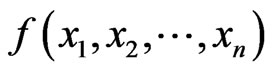is 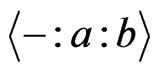canalyzing if there exists 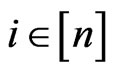such that

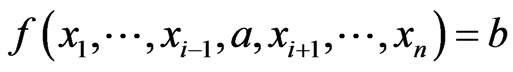, for all .

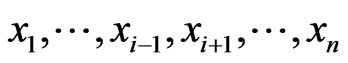4) The function 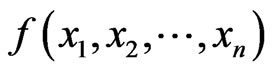is 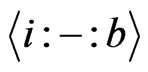canalyzing if there exists 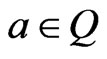such that 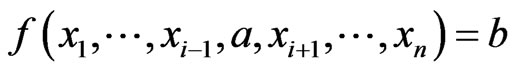, for all .

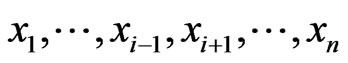5) The function 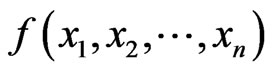is 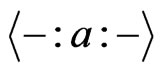canalyzing if there exist 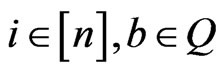such that 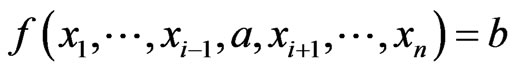, for all .

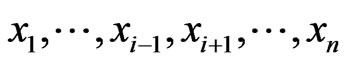6) The function 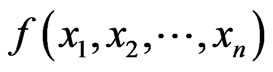is 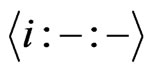canalyzing if there exist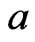, 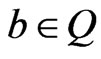such that 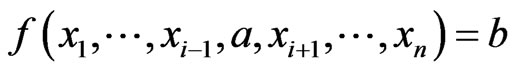, for all .

7) The function 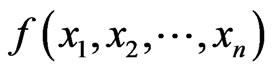is canalyzing if there exist 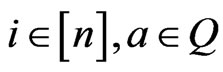such that 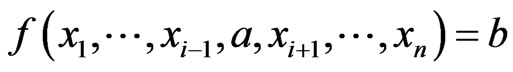, for all .

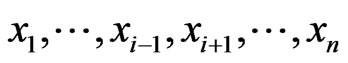8) The function is 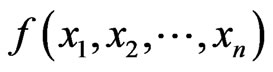is canalyzing if there exist 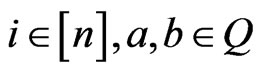such that 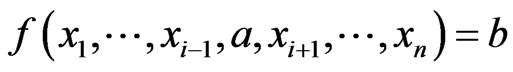, for all .

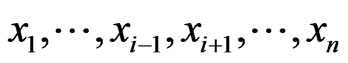By abuse of notation, we also use 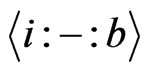to stand for the set of all the canalyzing functions, 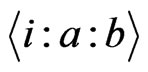will stand for the set of all the 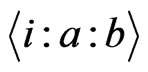canalyzing functions and etc. We use 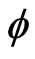to stand for the empty set.

By the definitions, we immediately have the following propositions.

Proposition 2.2 If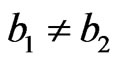, then.

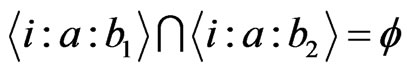Proposition 2.3 If 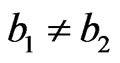and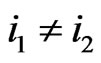, then .

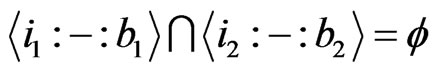By the definitions, we have

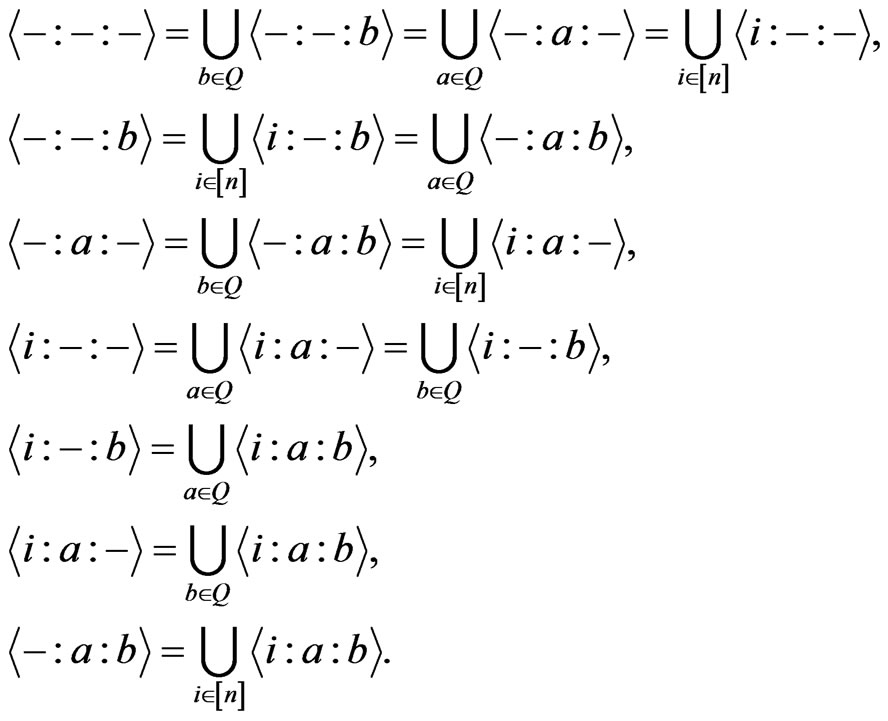
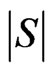For any set, we use to stand for its cardinality.

We use 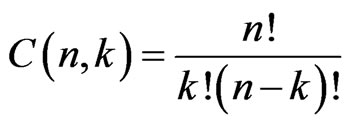to stand for the binomial coefficients. As usual, 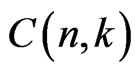should be explained as zero once.

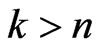Obviously, for the above notations, the cardinality are same for different values of 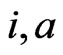and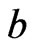. In other wordswe have,

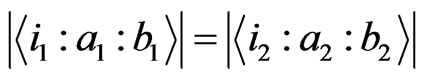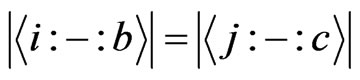, and etc.

3. Enumeration

Theorem 3.1 Given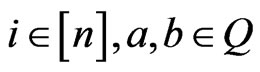, the number of

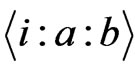canalyzing functions is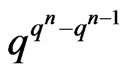. In other wordswe have.

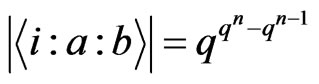Proof: A function in the set 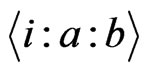is uniquely determined by its value on inputs 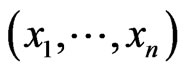with 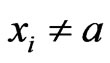. There are 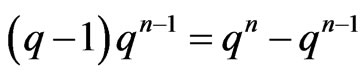such inputs, and the function can take different values. Thus . □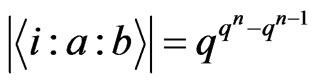

Because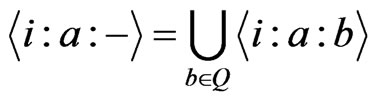, by Proposition 2.2we get Theorem 3.2 The number of all the 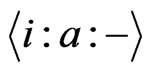canalyzing function is

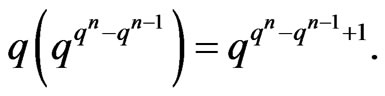
Lemma 3.3 We have 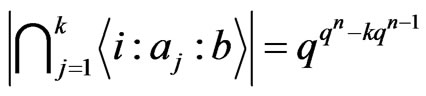for any.

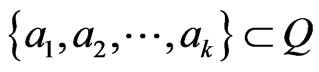Proof: A function in the set 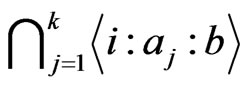is uni quely determined by it values on inputs with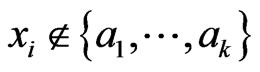. There are 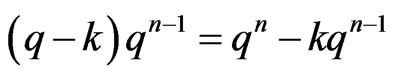such inputs. □

Theorem 3.4 Given and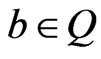, the number of 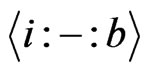canalyzing functions is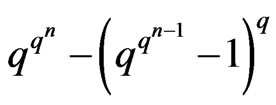. In other words, we have.

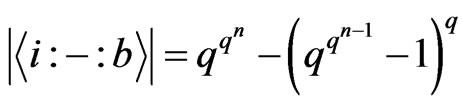Proof: By Inclusion and Exclusion Principle, we have

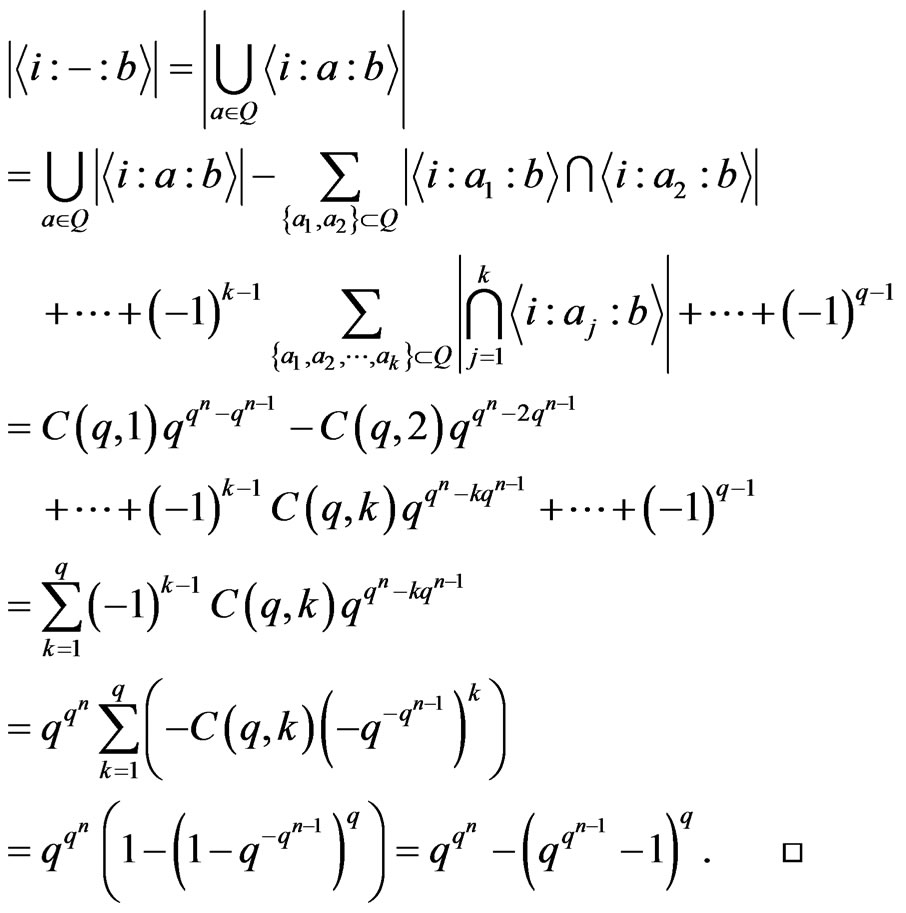
Similar to Lemma 3.3, we have Lemma 3.5 If, then

.

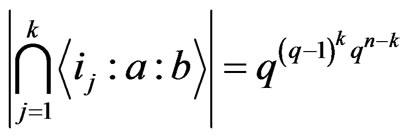Based on this lemma, we can get the following result.

Theorem 3.6 We have

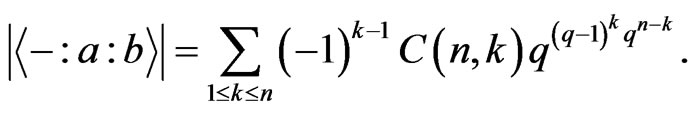
Proof: By Inclusion and Exclusion Principle, we have

From the above theorem, we can get the following result.

Theorem 3.7 We have

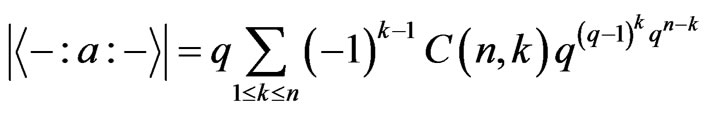
Proof: Because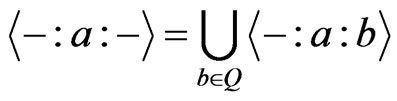, by Theorem 3.6, we just need to show if 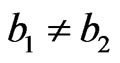. Suppose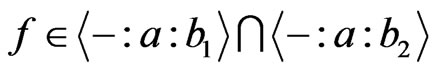, then there exist 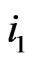and 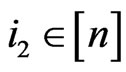such that

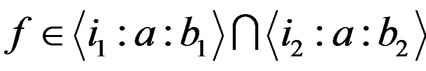since.

If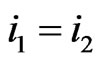, we get a contradiction by Proposition 2.2. If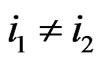, we get a contradiction by Proposition 2.3 since 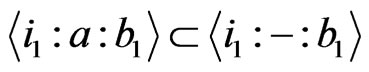and. □

Now, we are going to find the formula for the number of all the canalyzing functions with given canalyzed value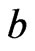. In other words, the formula of.

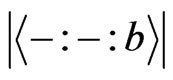Let 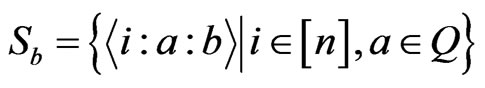for any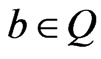. By Inclusion and Exclusion Principle, we have

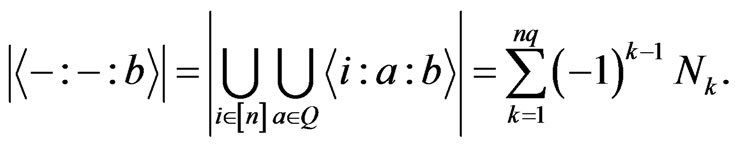
where

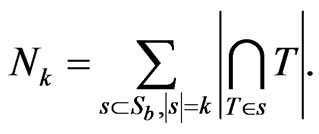
In order to evaluate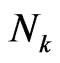, we write all the members in 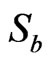as the following 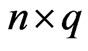matrix.

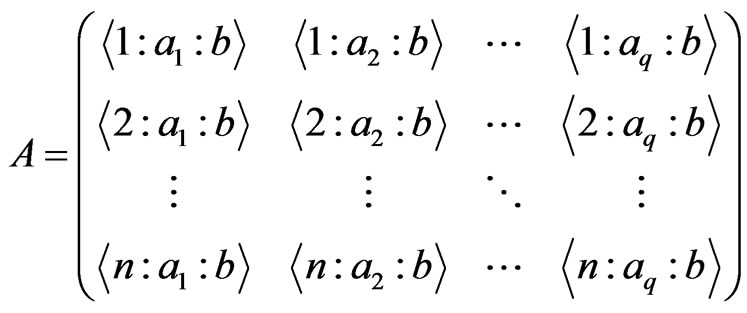
For any 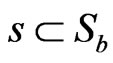with, we will choose 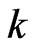elements from the above matrix to form.

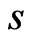Suppose 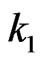of its elements are from the first row (there are 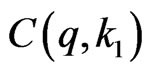ways to do so). Let these 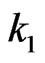elements be.

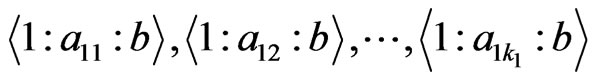Suppose 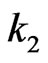of its elements are from the second row (there are 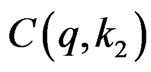ways to do so). Let these 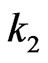elements be.

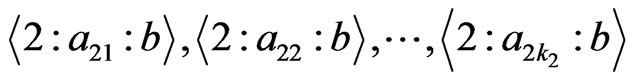Suppose 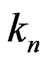of its elements are from the last row (there are 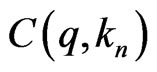ways to do so). Let these 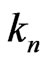elements be.

.

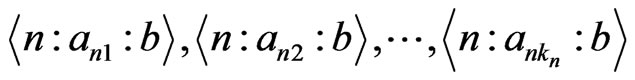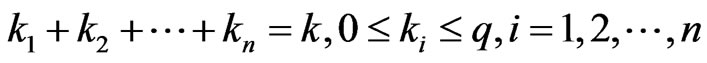Similar to Lemma 3.3, we have Lemma 3.8 Let 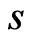be the subset of 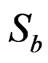as mentioned above, then.

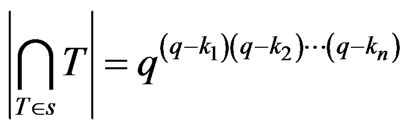Hence,

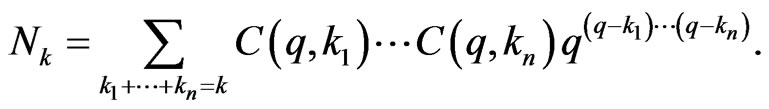
We get Theorem 3.9 For any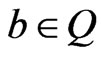, we have

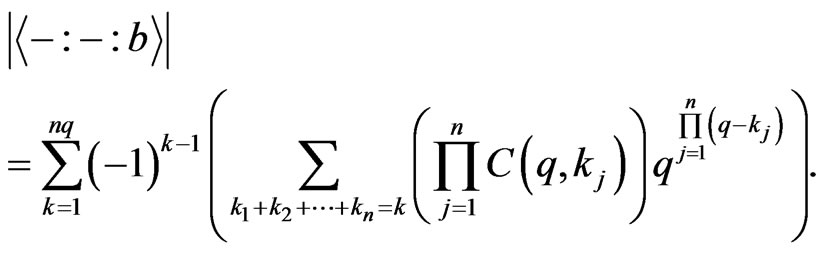
In order to evaluate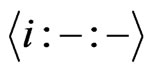, we need two more lemmas. Their proofs are similar to that of Lemma 3.3 and we omit them.

Lemma 3.10 If 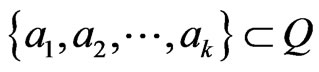and 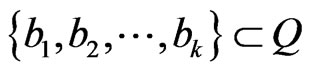, then

.

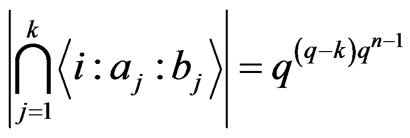Lemma 3.11 If 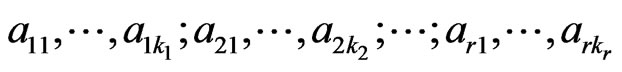are distinct elements of, 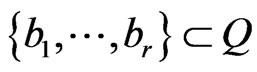. Then,

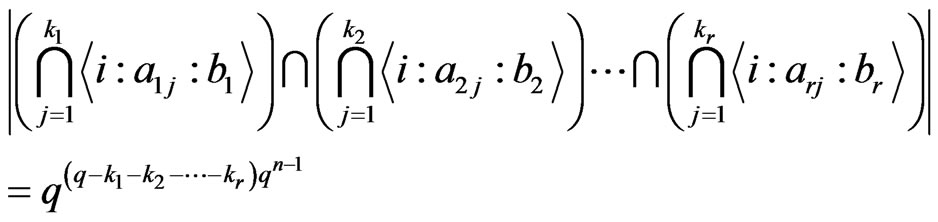
Now, we are ready to find the cardinality of.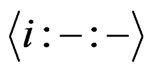

Theorem 3.12 We have

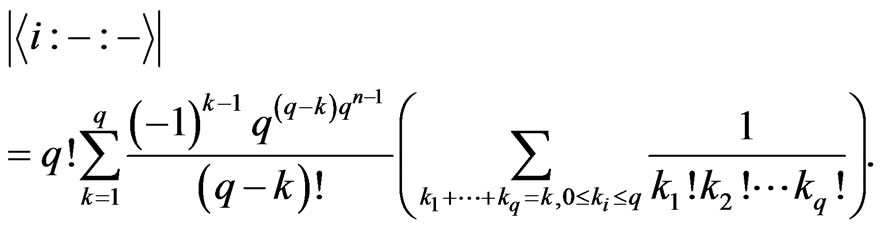
Proof: First, we have.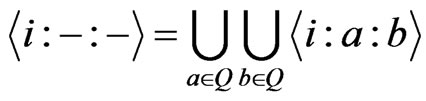

Let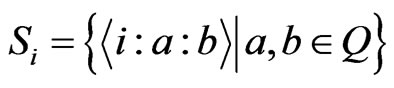, we get

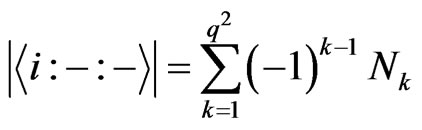. Where

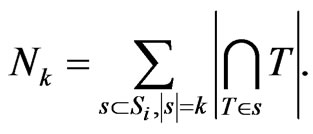
In order to evaluate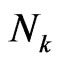, we write all the elements in 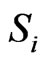as the following 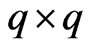matrix.

For any 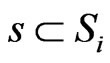with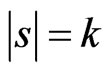, we will choose 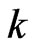elements from the above matrix to form.

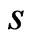Suppose of it elements are from the first row (There are 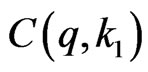ways to do so). Let these 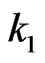elements be.

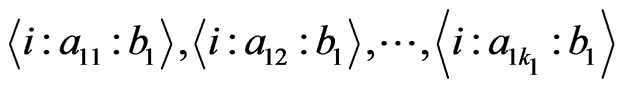Suppose 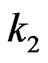of its elements are from the second row, we must choose these elements from different columns, otherwise the intersection will be 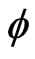by Proposition 2.2 (There are 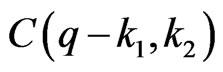ways to do so). Let these 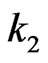elements be

Suppose 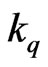of its elements are from the last row (There are ways to do so). Let these 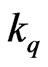elements be

.

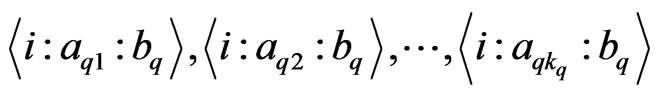where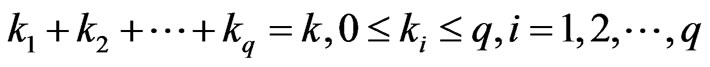. We have

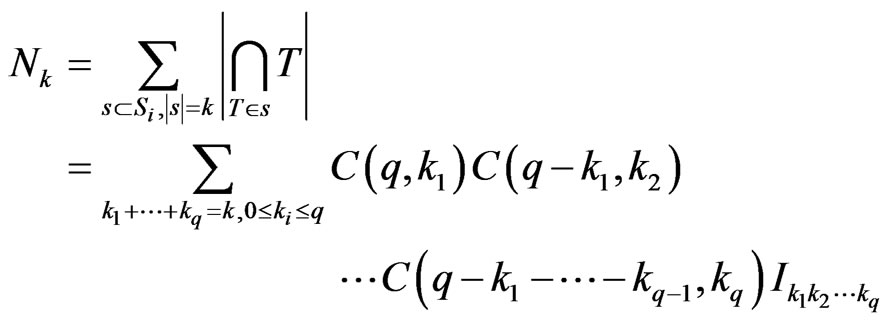
where

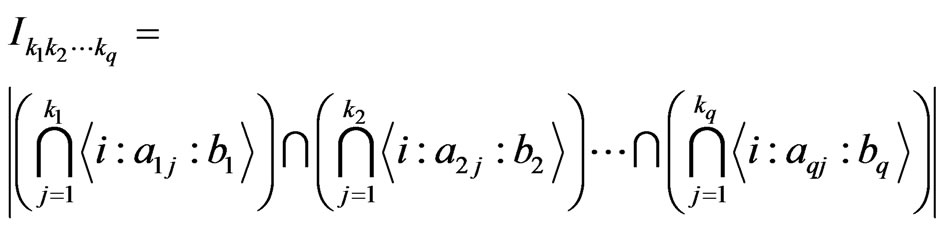
By Lemma 3.11, we know

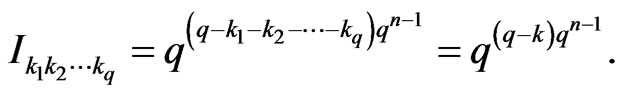
This number is zero if.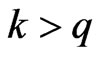

A straightforward computing shows that

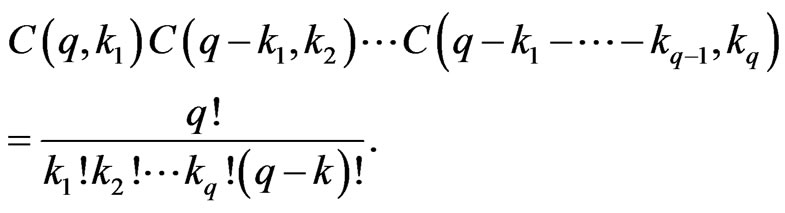
Hence, we get

□

Now we begin to evaluate.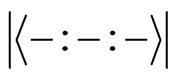

Theorem 3.13 We have

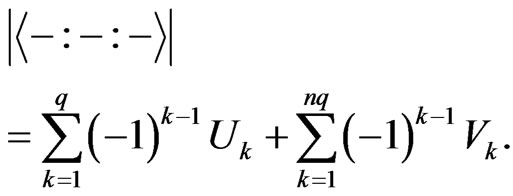
where

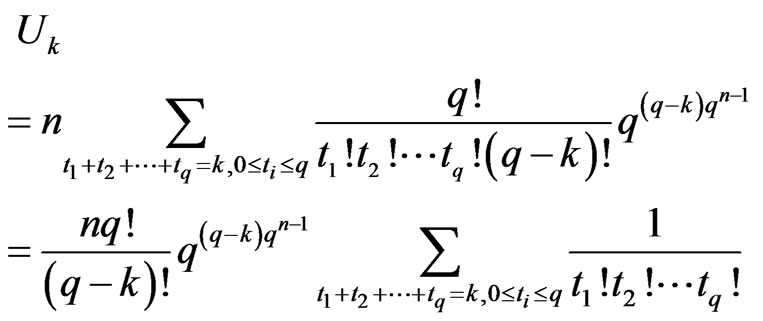
and

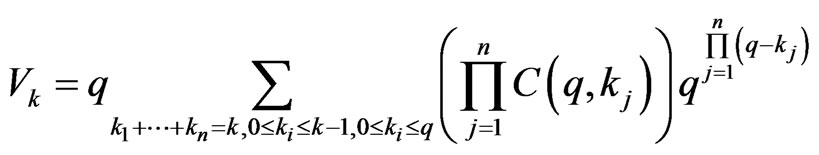
Proof: Let

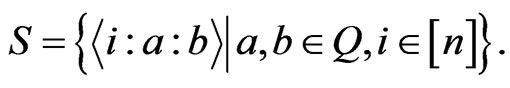
We have

and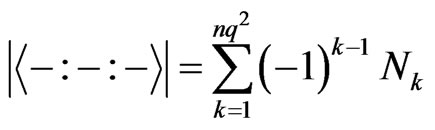, where

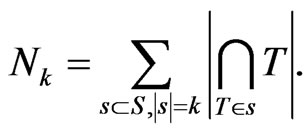
We write all the 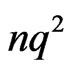elements of S as the following matrices.

We combine all the above 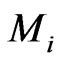to form a 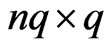matrix 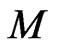whose first 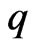rows are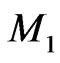, the second 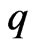rows are 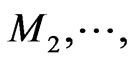the last 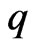rows are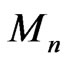. In other words, we have

We are going to choose 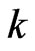elements from 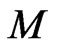to form the intersection. In order to get a possible non empty intersection, we know all these 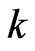elements must come from either the same 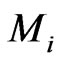(for some fixed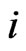) or all of them from the same column of 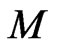by Proposition 2.3.

Each is in fact the transpose of 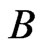and each column of is all the elements of 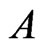(As sets, they are equal). Hence, a typical intersection is either the one in Theorem 3.9 or the one in Theorem 3.12. But these two cases are not disjoint.

Suppose we choose 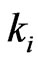elements from

.

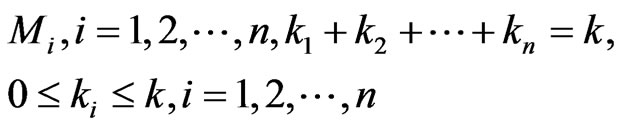If there exist 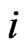such that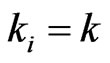, then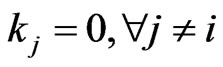. This implies the intersection looks like the one in Lemma 3.11 and.

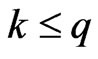If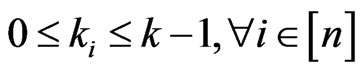, then the intersection looks like the one in Lemma 3.8 and.

The above two cases are disjoint now. By Lemma 3.11 and Lemma 3.8, we get

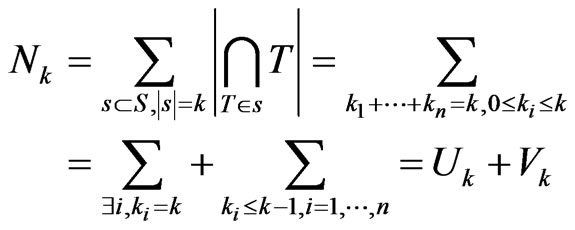
where (Note: there are matrices 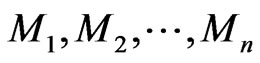and 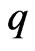columns of)

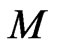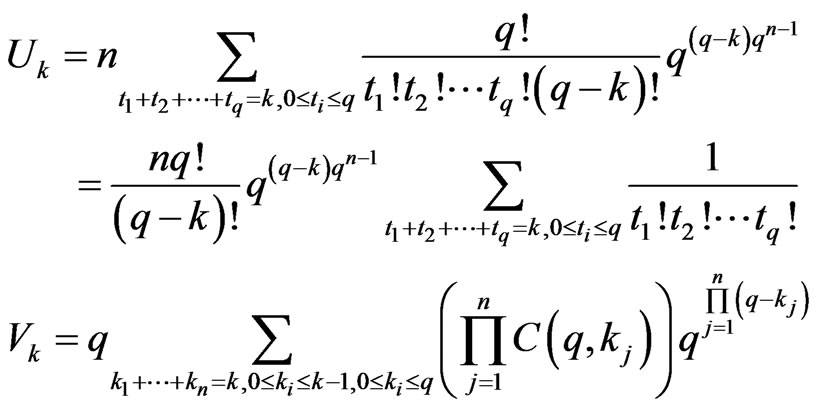
Hence,

□

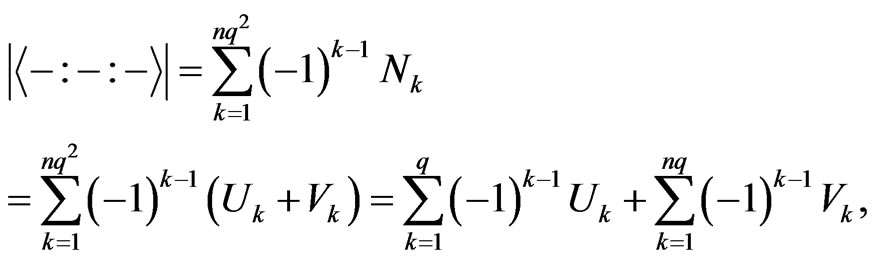In the following, we will reduce the formula

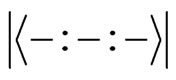
when 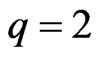and compare it with the one in [1]. We have

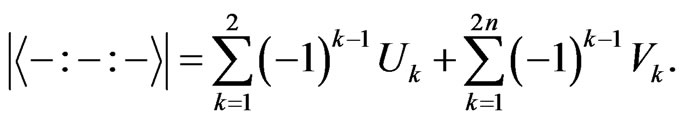
where

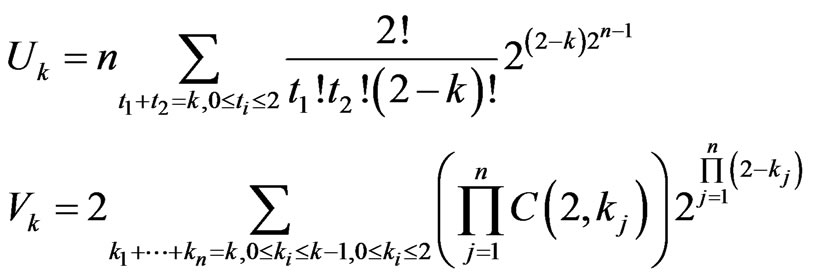
A simple calculation shows that

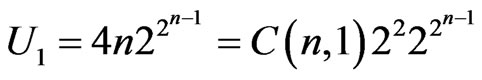
and

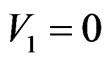since the condition of the sum is not satisfied.

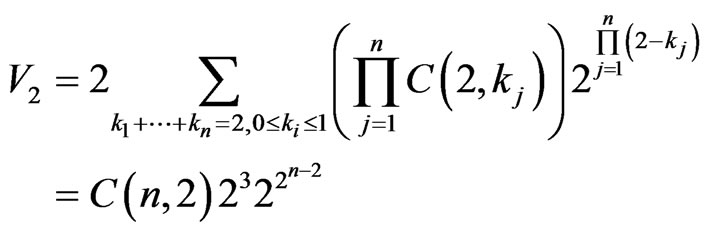
Note, 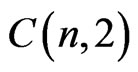is the number of solutions of the equation.

When,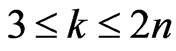

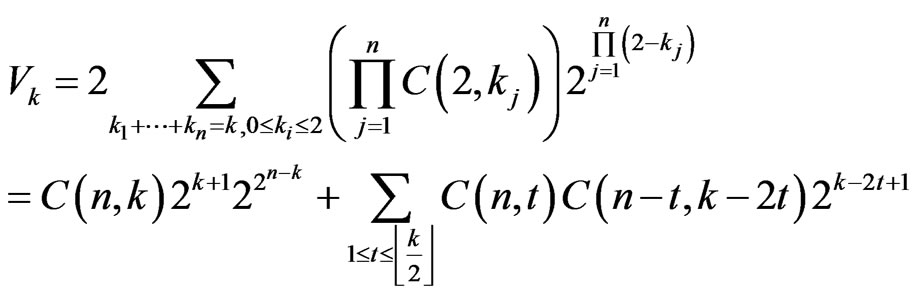
Note, 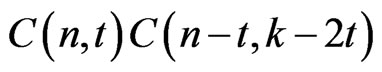is the number of solutions of the equation, 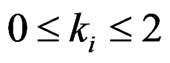with exactly 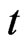components equal to 2.

hence, when,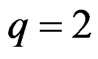

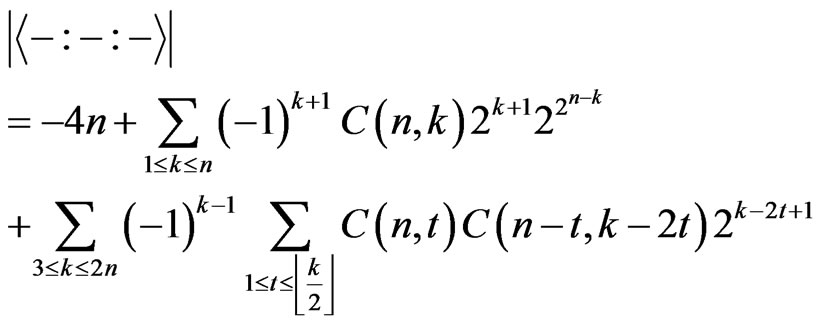
When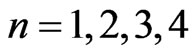, one can obtain (without calculator) the sequence 4, 14, 120, 3514. These results are consistent with those in [1]. By [1], the cardinality of 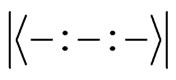should be

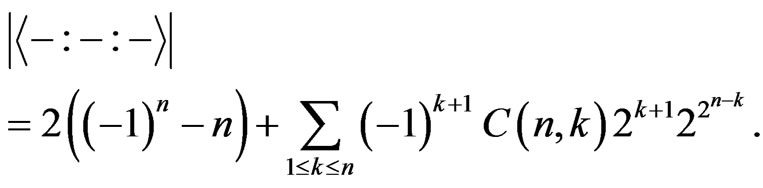
So, we obtain the following combinatorial identity(for any positive integer).

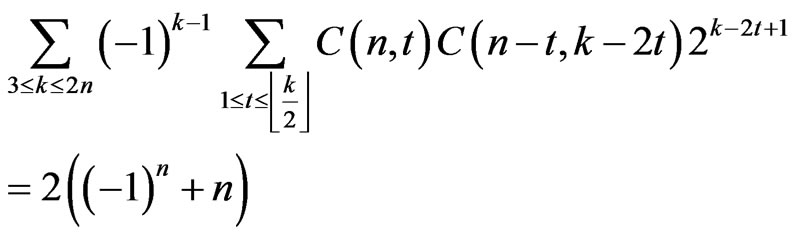
The left sum should be explained as 0 if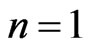. As usual, 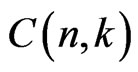is 0 if.

From Theorem 3.1, we know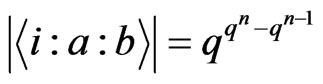since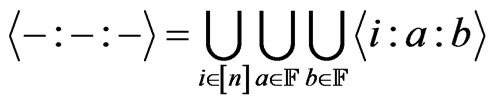, we obtain

.

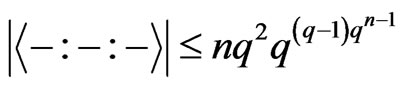In order to get an intuitive idea about the magnitude of all the cardinality numbers, We will find their asymptote as 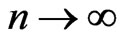or.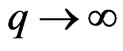

We have the following notation Definition 3.14 We call 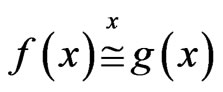if .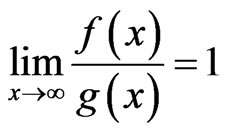

Now, we can list all the cardinalities asymptotically.

Theorem 3.15 If 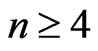and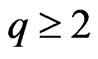, then

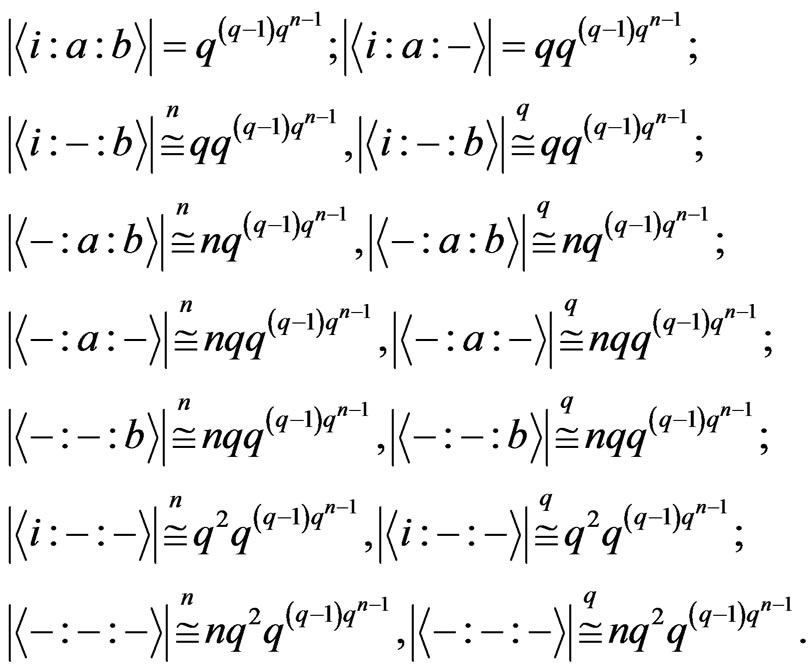
Proof:

The first two rows are Theorem 3.1 and Theorem 3.2.

We will give a proof of the last row, the others are similar and easier.

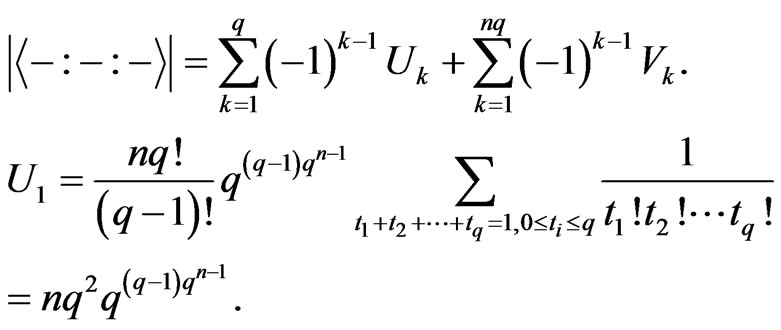
When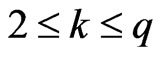, we have

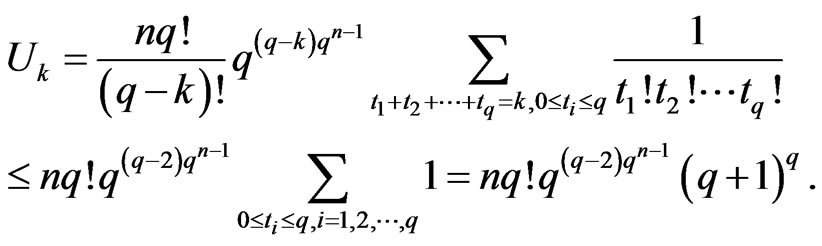
Hence,

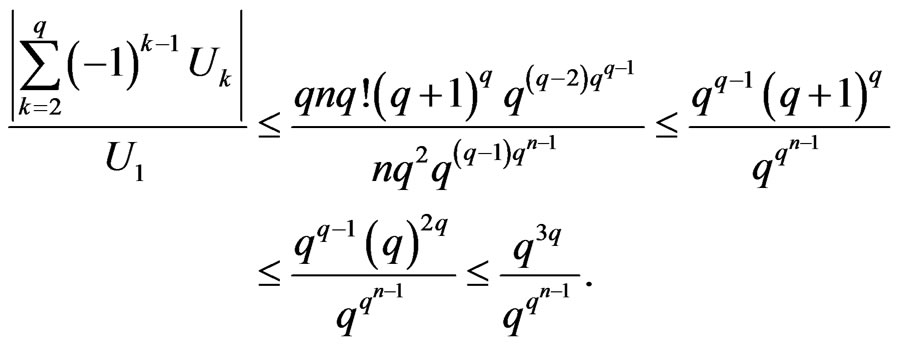
So,.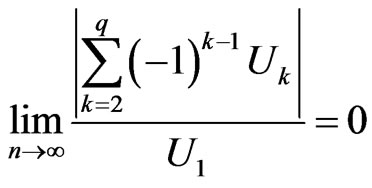

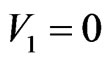since the condition of the sum is not satisfied.

When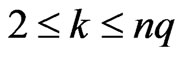, we have

Note,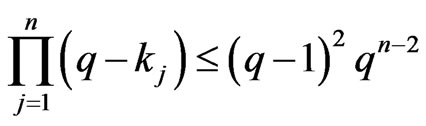. Hence,

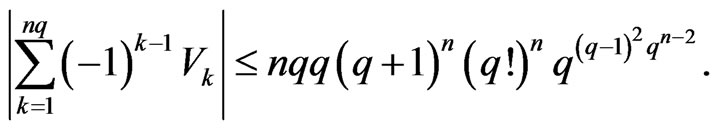
We obtain

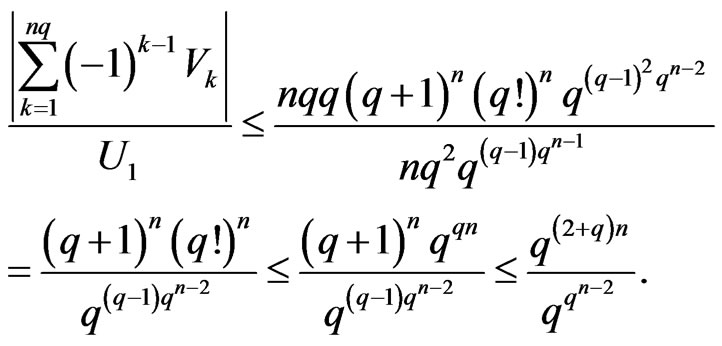
Hence,

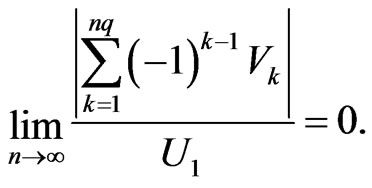
In summary, we obtain

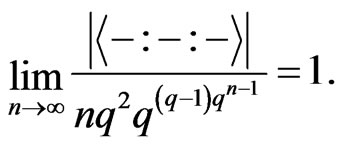
In other words,

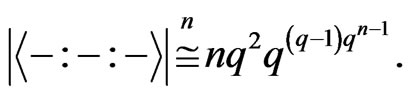
From the above proof, it is also clear that we have

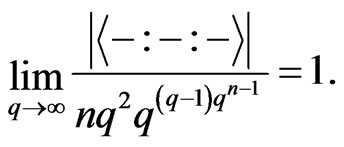
In other words,

□

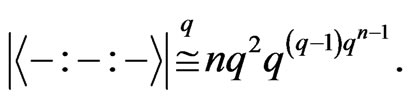
When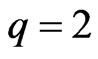, the first equation of the last row in the above theorem has been obtained in [1].

4. Conclusion

In this paper, we generalized the definition of Boolean canalyzing functions to the functions of multi-state case. Using Inclusion and Exclusion Principle, we get formulas for the cardinality all such functions and the cardinalities of its various subsets. When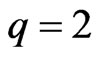, we derive an interesting combinatorial identity by equating our formula to the one in [1]. Finally, for a better understanding to the magnitudes, we provide all the asymptotes of these cardinalities as eithe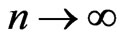r or.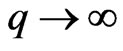

5. Acknowledgements

This work was initiated when the first and the third authors visited Virginia Bioinformatics Institute at Virginia Tech in June 2010. We thank Alan Veliz-Cuba and Franzeska Hinkelmann for many useful discussions. The first and the third authors thank Professor Reinhard Laubenbacher for his hospitality and for introducing them to Discrete Dynamical Systems. The third author was supported in part by a Research Initiation Program (RIP) award at Winston-Salem State University.

We greatly appreciate an anonymous reader. Because of his insightful comments, in this paper, the proofs for many lemmas are simplified, the results are more general (On any finite set instead of finite field).

REFERENCES

NOTES

^*Supported by an award from the USA DoD # W911NF-11-10166.

^*Corresponding author.