Open Journal of Discrete Mathematics
Vol.2 No.3(2012), Article ID:21145,6 pages DOI:10.4236/ojdm.2012.23019
Some New Results on Prime Graphs
1Saurashtra University, Rajkot, India
2St. Xavier’s College, Ahmedabad, India
Email: samirkvaidya@yahoo.co.in, udayan64@yahoo.com
Received May 6, 2012; revised June 13, 2012; accepted June 25, 2012
Keywords: Prime Labeling; Prime Graph; Strongly Prime Graph
ABSTRACT
We investigate prime labeling for some graphs resulted by identifying any two vertices of some graphs. We also introduce the concept of strongly prime graph and prove that the graphs Cn, Pn, and K1,n are strongly prime graphs. Moreover we prove that Wn is a strongly prime graph for every even integer n ≥ 4.
1. Introduction
We begin with finite, undirected and non-trivial graph  with the vertex set
with the vertex set 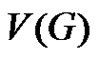 and the edge set
and the edge set . Throughout this work
. Throughout this work 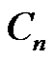 denotes the cycle with
denotes the cycle with 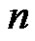 vertices and
vertices and 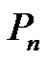 denotes the path on
denotes the path on 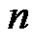 vertices. In the wheel
vertices. In the wheel  the vertex corresponding to
the vertex corresponding to 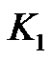 is called the apex vertex and the vertices corresponding to
is called the apex vertex and the vertices corresponding to 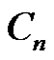 are called the rim vertices, where
are called the rim vertices, where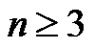 . The star
. The star 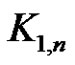 is a graph with one vertex of degree
is a graph with one vertex of degree  called apex and
called apex and 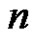 vertices of degree one called pendant vertices. Throughout this paper
vertices of degree one called pendant vertices. Throughout this paper 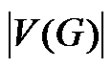 and
and 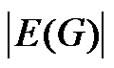 denote the cardinality of vertex set and edge set respectively.
denote the cardinality of vertex set and edge set respectively.
For various graph theoretic notation and terminology we follow Gross and Yellen [1] while for number theory we follow Burton [2]. We will give brief summary of definitions and other information which are useful for the present investigations.
Definition 1.1: If the vertices are assigned values subject to certain condition(s) then it is known as graph labeling.
Vast amount of literature is available in printed as well as in electronic form on different kind of graph labeling problems. For a dynamic survey of graph labeling problems along with extensive bibliography we refer to Gallian [3].
Definition 1.2: A prime labeling of a graph 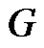 is an injective function
is an injective function 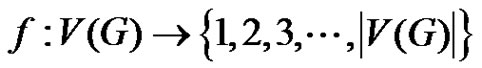 such that for every pair of adjacent vertices
such that for every pair of adjacent vertices  and
and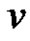 ,
, . The graph which admits a prime labeling is called a prime graph.
. The graph which admits a prime labeling is called a prime graph.
The notion of a prime labeling was originated by Entringer and was discussed in a paper by Tout et al. [4]. Many researchers have studied prime graphs. For e.g. Fu and Huang [5] have proved that 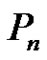 and
and  are prime graphs. Lee et al. [6] have proved that
are prime graphs. Lee et al. [6] have proved that 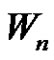 is a prime graph if and only if
is a prime graph if and only if 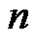 is even. Deretsky et al. [7] have proved that
is even. Deretsky et al. [7] have proved that 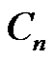 is a prime graph.
is a prime graph.
Definition 1.3: Let u and v be two distinct vertices of a graph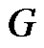 . A new graph
. A new graph 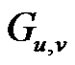 is constructed by identifying (fusing) two vertices u and v by a single new vertex x such that every edge which was incident with either u or v in
is constructed by identifying (fusing) two vertices u and v by a single new vertex x such that every edge which was incident with either u or v in  is now incident with x in
is now incident with x in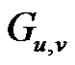 .
.
Vaidya and Kanani [8] have established that the graph obtained by identifying any two vertices 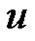 and
and 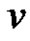 (with
(with ) of
) of  (
( ) is a prime graph. The switching invariance of various prime graphs is discussed by Vaidya and Prajapati [9]. In the present paper we investigate further results on prime graphs.
) is a prime graph. The switching invariance of various prime graphs is discussed by Vaidya and Prajapati [9]. In the present paper we investigate further results on prime graphs.
Bertrand’s Postulate 1.4: For every positive integer 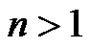 there is a prime
there is a prime 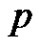 such that
such that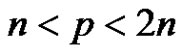 .
.
2. Prime Labeling of Some Graphs
Theorem 2.1: The graph obtained by identifying any two vertices of  is a prime graph.
is a prime graph.
Proof: The result is obvious for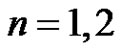 . Therefore we start with
. Therefore we start with . Let
. Let  be the apex vertex and
be the apex vertex and 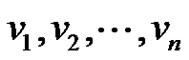 be the consecutive pendant vertices of
be the consecutive pendant vertices of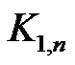 . Due to the nature of
. Due to the nature of  two vertices can be identified in following two possible ways:
two vertices can be identified in following two possible ways:
Case 1: The apex vertex 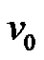 is identified with any of the pendant vertices (say
is identified with any of the pendant vertices (say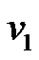 ). Let the new vertex be
). Let the new vertex be 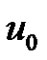 and the resultant graph be
and the resultant graph be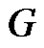 .
.
Then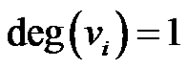 , for
, for  and
and 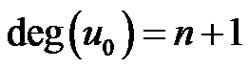 as there is a loop incident at
as there is a loop incident at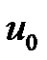 . Define
. Define 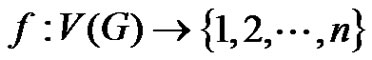 as
as 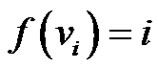 for
for 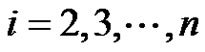 and
and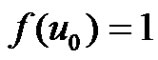 . Obviously f is an injection and
. Obviously f is an injection and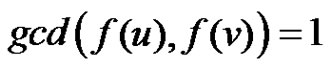 for every pair of adjacent vertices
for every pair of adjacent vertices and
and 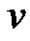 of
of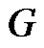 . Hence
. Hence  is a prime graph.
is a prime graph.
Case 2: Any two of the pendant vertices (say 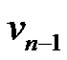 and
and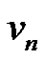 ) are identified. Let the new vertex be
) are identified. Let the new vertex be 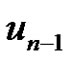 and the resultant graph be G. So in G,
and the resultant graph be G. So in G, 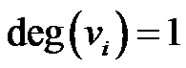 , for
, for 
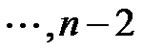 ,
, 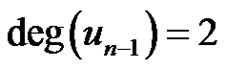 and
and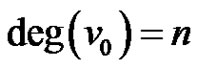 . Define
. Define  as
as 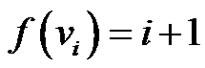 for
for 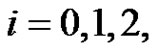
 and
and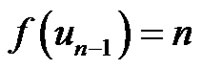 . Obviously f is an injection and
. Obviously f is an injection and 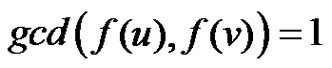 for every pair of adjacent vertices
for every pair of adjacent vertices  and
and 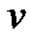 of
of . Hence
. Hence 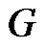 is a prime graph.
is a prime graph.
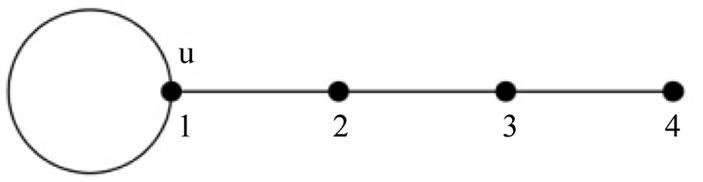
Illustration 2.2: The prime labeling of the graph obtained by identifying the apex vertex with a pendant vertex of 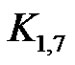 is shown in Figure 1.
is shown in Figure 1.
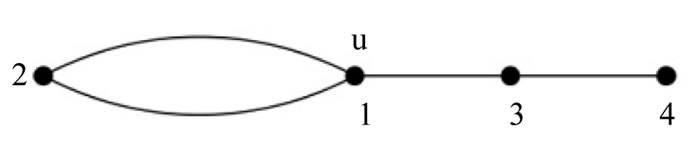
Illustration 2.3: The prime labeling of the graph obtained by identifying two of the pendant vertices of  is shown in Figure 2.
is shown in Figure 2.
Theorem 2.4: If 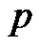 is a prime and
is a prime and 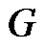 is a prime graph of order
is a prime graph of order  then the graph obtained by identifying two vertices with label 1 and
then the graph obtained by identifying two vertices with label 1 and 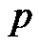 is also a prime graph.
is also a prime graph.
Proof: Let f be a prime labeling of 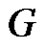 and
and 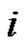 be the label of the vertex
be the label of the vertex 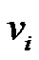 for
for . Moreover
. Moreover 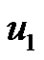 be the new vertex of the graph
be the new vertex of the graph  which is obtained by identifying
which is obtained by identifying 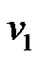 and
and 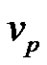 of
of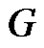 . Define
. Define 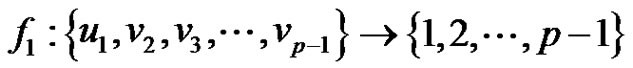 as
as
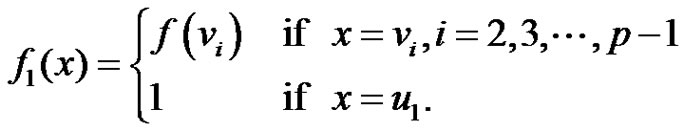
Then 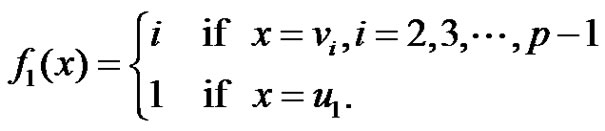
Obviously 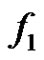 is an injection. For an arbitrary edge
is an injection. For an arbitrary edge 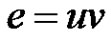 of
of  we claim that
we claim that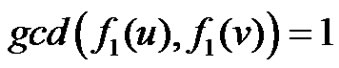 . To prove our claim the following cases are to be considered.
. To prove our claim the following cases are to be considered.
Case 1: If 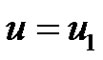 then
then 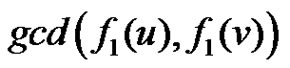 =
= 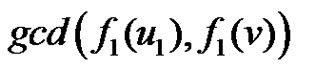 =
=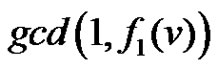 = 1.
= 1.
Case 2: If  and
and  then
then 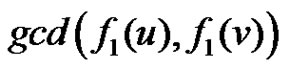 =
=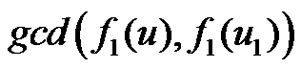 =
=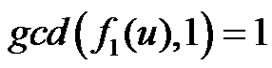 .
.
Case 3: If 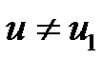 and
and 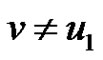 then
then  for some
for some 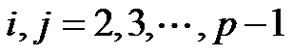 with
with  then
then 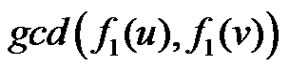 =
= 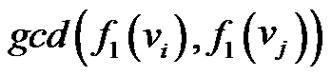 =
= 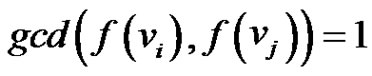 as
as 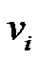 and
and 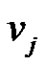 are adjacent vertices in the prime graph
are adjacent vertices in the prime graph 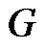 with the prime labelling
with the prime labelling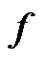 . Thus in all the possibilities
. Thus in all the possibilities  admits a prime labeling for
admits a prime labeling for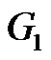 . Hence
. Hence 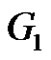 is a prime graph.
is a prime graph.
Illustration 2.5: In the following Figures 3 and 4 prime labeling of a graph  of order 5 and the prime labeling for the graph
of order 5 and the prime labeling for the graph 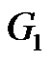 obtained by identifying the vertices of
obtained by identifying the vertices of  with label 1 and 5 are shown.
with label 1 and 5 are shown.
Theorem 2.6: The graph obtained by identifying any two vertices of 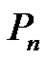 is a prime graph.
is a prime graph.
Proof: Let  be the vertices of
be the vertices of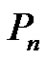 . Let
. Let 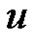 be the new vertex of the graph
be the new vertex of the graph 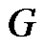 obtained by identifying two distinct vertices
obtained by identifying two distinct vertices 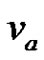 and
and 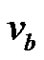 of
of . Then
. Then  is nothing but a cycle (possibly loop) with at the most two
is nothing but a cycle (possibly loop) with at the most two
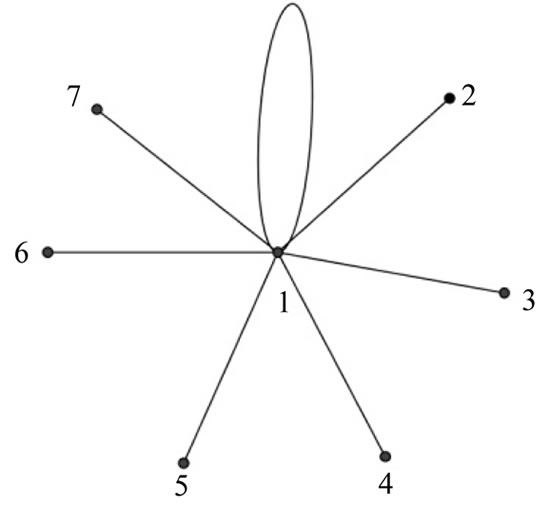
Figure 1. The prime labeling of the graph obtained by identifying the apex vertex with a pendant vertex in K1,7.
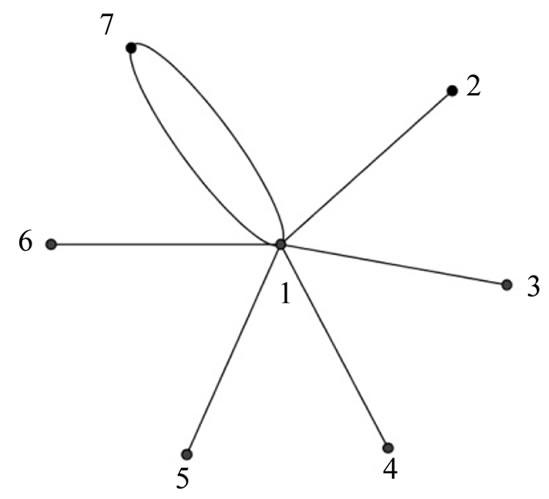
Figure 2. The prime labeling of the graph obtained by identifying two of the pendant vertices in K1,7.

Figure 3. The prime labeling of a graph of order five.
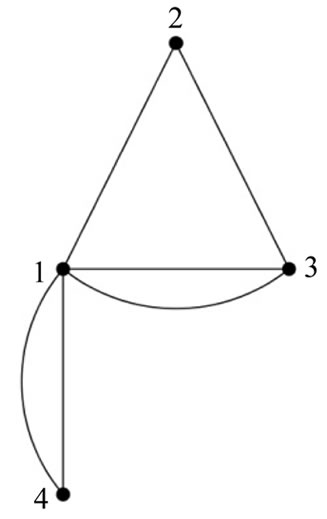
Figure 4. The prime labeling of the graph obtained by identifying the vertices of Figure 3 with label 1 and 5.
paths attached at . Such graph is a prime graph as proved in Vaidya and Prajapati [10].
. Such graph is a prime graph as proved in Vaidya and Prajapati [10].
Illustration 2.7: In the following Figures 5-9 prime labelings for 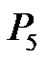 and the graphs obtained by identifying two vertices in various possible ways are shown.
and the graphs obtained by identifying two vertices in various possible ways are shown.
3. Strongly Prime Graphs
Definition 3.1: A graph G is said to be a strongly prime

Figure 5. A prime labeling of P5.
graph if for any vertex 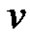 of
of 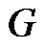 there exits a prime labeling f satisfying
there exits a prime labeling f satisfying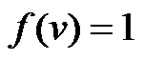 .
.
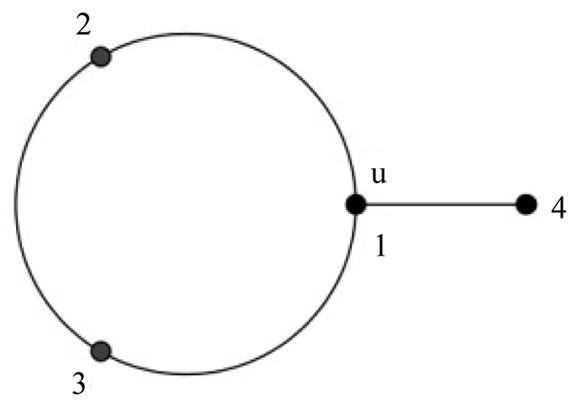
Observation 3.2: 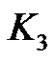 is a strongly prime graph as any vertex of
is a strongly prime graph as any vertex of 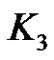 can be assigned label 1 and the remaining vertices can be assigned label 2 and 3 as shown in Figure 10.
can be assigned label 1 and the remaining vertices can be assigned label 2 and 3 as shown in Figure 10.
Observation 3.3: If 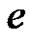 is an edge of
is an edge of 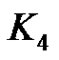 then
then 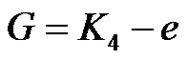 is a prime graph (see Figure 11) but it is not a strongly prime graph. If possible either of the vertices of
is a prime graph (see Figure 11) but it is not a strongly prime graph. If possible either of the vertices of  with degree 2 can be assigned the label 1. Suppose
with degree 2 can be assigned the label 1. Suppose 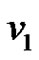 is assigned the label 1 then available vertex labels for the remaining three vertices of
is assigned the label 1 then available vertex labels for the remaining three vertices of 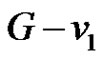 are 2, 3 and 4. Consequently the vertices corresponding to the labels 2 and 4 are adjacent in
are 2, 3 and 4. Consequently the vertices corresponding to the labels 2 and 4 are adjacent in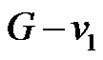 . See Figure 12.
. See Figure 12.
Observation 3.4: Every spanning subgraph of a strongly prime graph is a strongly prime graph. Because every spanning subgraph of a prime graph is a prime graph as proved by Seoud and Youssef [11].
Theorem 3.5: Every path is a strongly prime graph.
Proof: Let 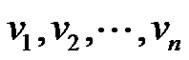 be the consecutive vertices of
be the consecutive vertices of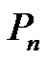 . If
. If 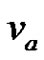 is any arbitrary vertex of
is any arbitrary vertex of 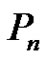 then we have the following possibilities:
then we have the following possibilities:
Case 1: If  is either of the pendant vertices (say
is either of the pendant vertices (say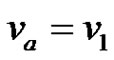 ) then the function
) then the function 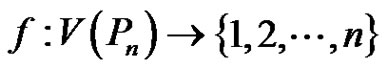 defined by
defined by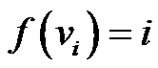 , for all
, for all , is a prime labeling for
, is a prime labeling for 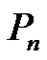 with
with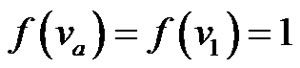 .
.
Case 2: If 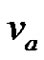 is not a pendant vertex then
is not a pendant vertex then  for some
for some 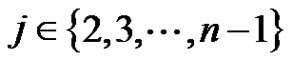 then the function
then the function 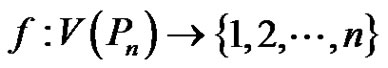 defined by
defined by
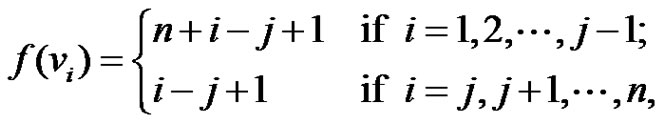
is a prime labeling with .
.
Thus from the cases described above 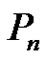 is a strongly prime graph.
is a strongly prime graph.
Illustration 3.6: It is possible to assign label 1 to arbitrary vertex of 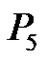 in order to obtain different prime labeling as shown in Figures 13-18.
in order to obtain different prime labeling as shown in Figures 13-18.
Theorem 3.7: Every cycle is a strongly prime graph.
Proof: Let 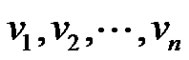 be the consecutive vertices of
be the consecutive vertices of . Let
. Let 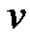 be an arbitrary vertex of
be an arbitrary vertex of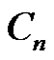 . Then
. Then 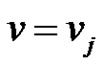 for some
for some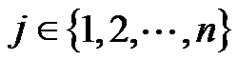 . The function
. The function 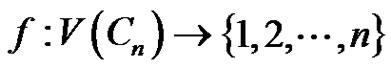 defined by
defined by

is a prime labeling for  with
with . Thus
. Thus 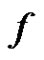 admits prime labeling as well as it is possible to assign label 1 to any arbitrary vertex of
admits prime labeling as well as it is possible to assign label 1 to any arbitrary vertex of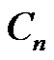 . That is
. That is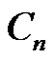 , is strongly prime graph.
, is strongly prime graph.
Theorem 3.8: 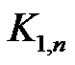 is a strongly prime graph.
is a strongly prime graph.
Proof: For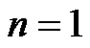 , 2 the respective graphs
, 2 the respective graphs 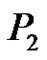 and
and  are strongly prime graphs as proved in the Theorem 3.5.
are strongly prime graphs as proved in the Theorem 3.5.

Figure 10. A strongly prime labeling of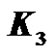 .
.
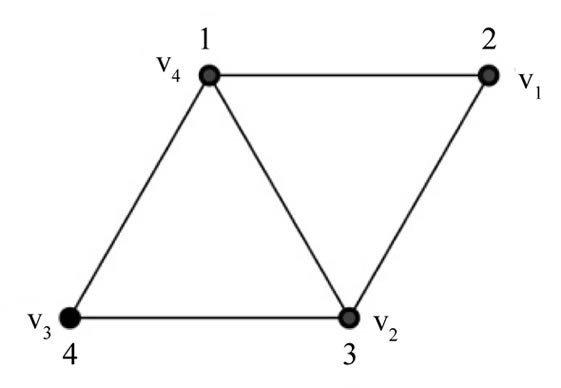
Figure 11. A prime labeling of .
.
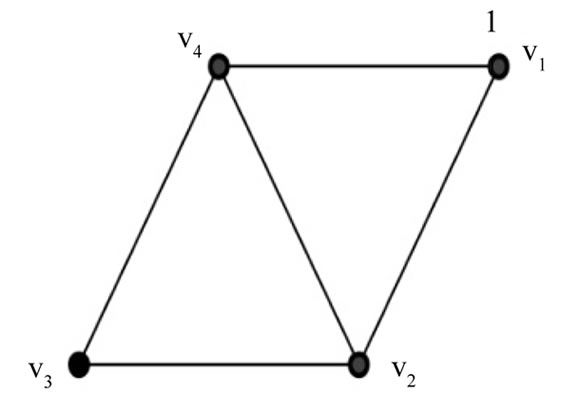
Figure 12.  is not a strongly prime graph.
is not a strongly prime graph.
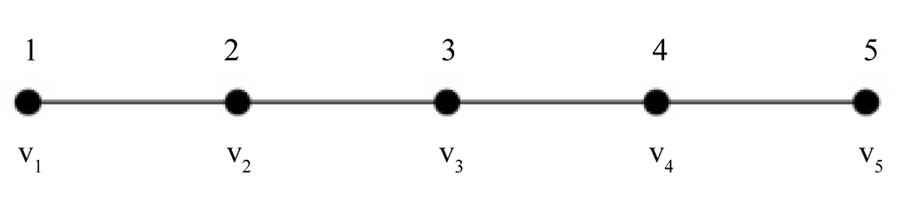
Figure 13. A prime labeling of 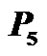 having
having  as label 1.
as label 1.

Figure 14. A prime labeling of  having
having 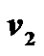 as label 1.
as label 1.

Figure 15. A prime labeling of 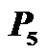 having
having 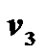 as label 1.
as label 1.

Figure 16. A prime labeling of P5 having v4 as label 1.

Figure 17. A prime labeling of 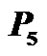 having
having 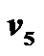 as label 1.
as label 1.

Figure 18. A prime labeling of 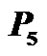 having
having  as label 1.
as label 1.
For 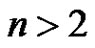 let
let  be the apex vertex and
be the apex vertex and 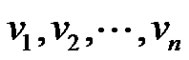 be the pendant vertices of
be the pendant vertices of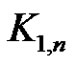 .
.
If 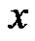 is any arbitrary vertex of
is any arbitrary vertex of 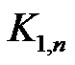 then we have the following possibilities:
then we have the following possibilities:
Case 1: If 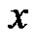 is the apex vertex then
is the apex vertex then . Then the function
. Then the function 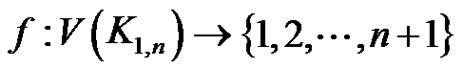 defined by
defined by 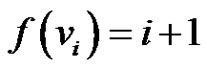 for
for 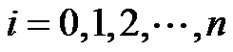 is a prime labeling on
is a prime labeling on  with
with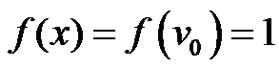 .
.
Case 2: If 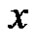 is one of the pendant vertices then
is one of the pendant vertices then  for some
for some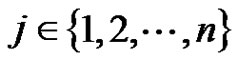 . Define
. Define ,
, 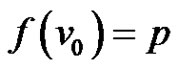 , where
, where 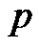 is the largest prime less than or equal to
is the largest prime less than or equal to 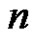 and the remaining
and the remaining 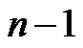 vertices are distinctly labeled from
vertices are distinctly labeled from . According to Bertrand’s postulate
. According to Bertrand’s postulate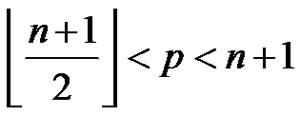 . Therefore
. Therefore 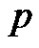 is co-prime to every integer from
is co-prime to every integer from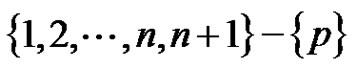 . Thus every edge
. Thus every edge 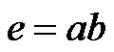 is incident to the apex vertex
is incident to the apex vertex  whose label is
whose label is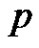 , thus
, thus 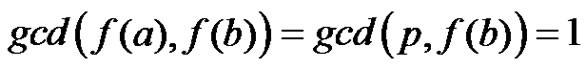 or
or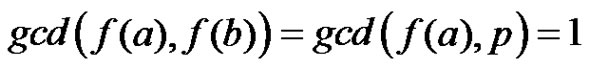 . Hence this function
. Hence this function 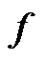 admits a prime labeling on
admits a prime labeling on  with
with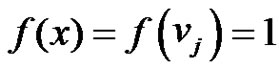 .
.
Thus from all the cases described above 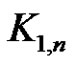 is a strongly prime graph.
is a strongly prime graph.
Illustration 3.9: It is possible to assign label 1 to arbitrary vertex of 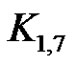 in order to obtain prime labeling as shown in Figures 19 and 20.
in order to obtain prime labeling as shown in Figures 19 and 20.
Theorem 3.10: 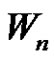 is a strongly prime graph for every even positive integer
is a strongly prime graph for every even positive integer .
.
Proof: Let 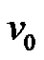 be the apex vertex and
be the apex vertex and  be the consecutive rim vertices of
be the consecutive rim vertices of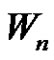 . Let
. Let  be an arbitrary vertex of
be an arbitrary vertex of . We have the following possibilities:
. We have the following possibilities:
Case 1:  is the apex vertex of
is the apex vertex of  that is
that is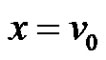 . Then the function
. Then the function 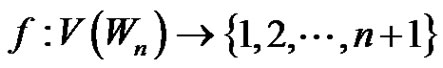 defined as
defined as
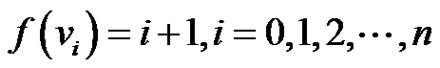 . (1)
. (1)
Obviously 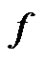 is an injection. For an arbitrary edge
is an injection. For an arbitrary edge  of
of 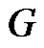 we claim that
we claim that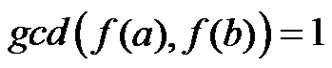 . To prove our claim the following subcases are to be considered.
. To prove our claim the following subcases are to be considered.
Subcase (1): if e = vivi+1 for some 

Figure 19. A prime labeling of K1,7 with the apex vertex as label 1.
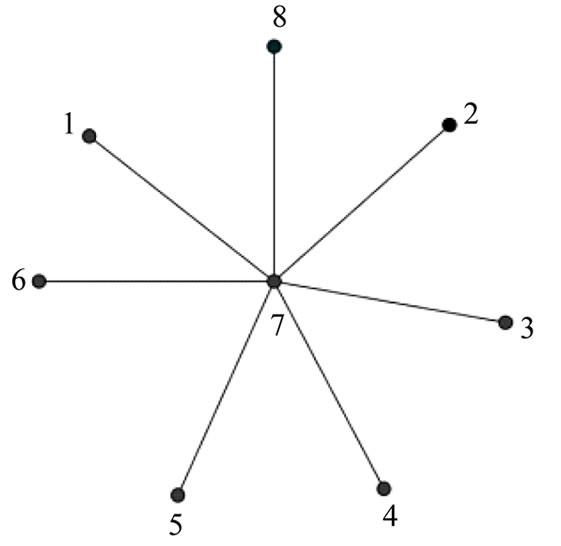
Figure 20. A prime labeling of K1,7 with a pendant vertex as label 1.
then  =
=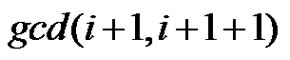 =
=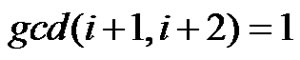 as
as  and
and 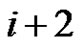 are consecutive positive integers.
are consecutive positive integers.
Subcase (2): if 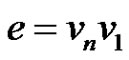 then
then 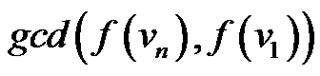 =
= 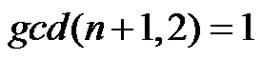 as
as 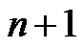 is an odd integer and it is not divisible by 2.
is an odd integer and it is not divisible by 2.
Subcase (3): if 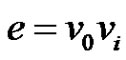 for some
for some 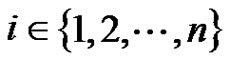 then
then 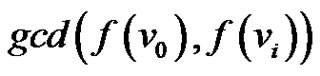 =
=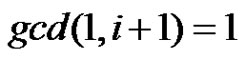 .
.
Case 2:  is one of the rim vertices. We may assume that
is one of the rim vertices. We may assume that 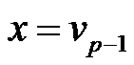 where
where 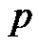 is the largest prime less than or equal to
is the largest prime less than or equal to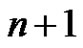 . According to the Bertrand’s Postulate such a prime
. According to the Bertrand’s Postulate such a prime 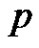 exists with
exists with . Define a function
. Define a function 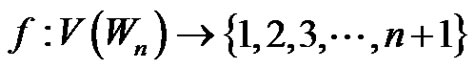 as
as
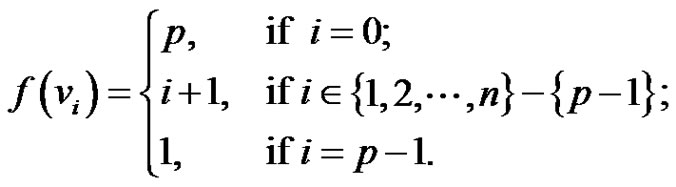 (2)
(2)
The only difference between the definition of labeling functions of (1) and (2) is the labels 1 and 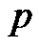 are interchanged. Then clearly
are interchanged. Then clearly 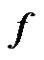 is an injection.
is an injection.
For an arbitrary edge 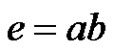 of
of 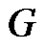 we claim that
we claim that . To prove our claim the following subcases are to be considered.
. To prove our claim the following subcases are to be considered.
Subcase (2): If 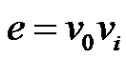 for some
for some 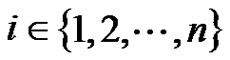 then
then 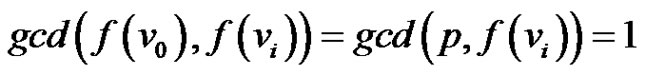 as
as 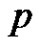 is co-prime to every integer from
is co-prime to every integer from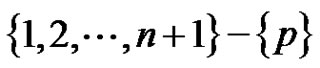 .
.
Subcase (2): If 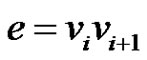 for some
for some 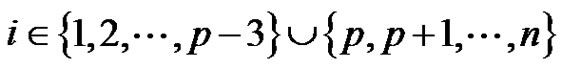 then
then  as
as 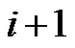 and
and  are consecutive positive integers.
are consecutive positive integers.
Subcase (3): If 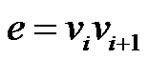 for
for 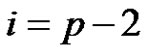 then
then 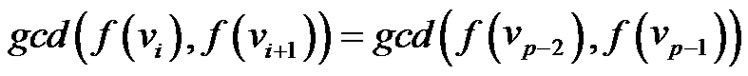 =
=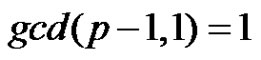 .
.
Subcase (4): If 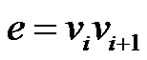 for
for  then
then 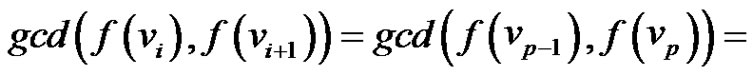
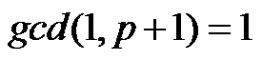
Thus in all the possibilities described above  admits prime labeling as well as it is possible to assign label 1 to any arbitrary vertex of
admits prime labeling as well as it is possible to assign label 1 to any arbitrary vertex of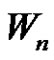 . That is,
. That is, 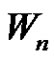 is a strongly prime graph for every even positive integer
is a strongly prime graph for every even positive integer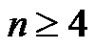 .
.
Illustration 3.11: It is possible to assign label 1 to arbitrary vertex of 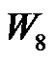 in order to obtain prime labeling as shown in Figures 21 and 22.
in order to obtain prime labeling as shown in Figures 21 and 22.
Corollary 3.12: The friendship graph 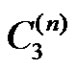 is a strongly prime graph.
is a strongly prime graph.
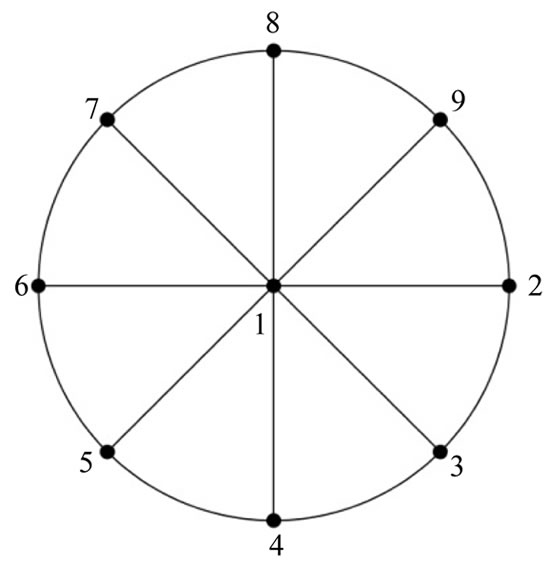
Figure 21. A prime labeling of W8 with the apex vertex as label 1.
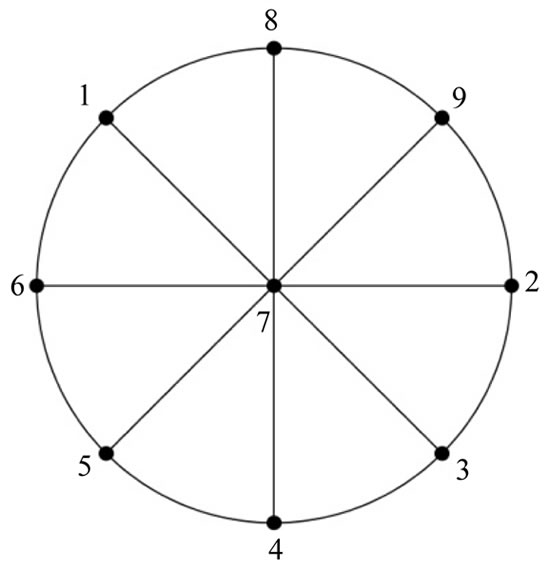
Figure 22. A prime labeling of W8 with a rim vertex as label 1.
Proof: The friendship graph  is a one point union of
is a one point union of 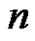 copies of
copies of . It can also be thought as a graph obtained by deleting every alternate rim edge of
. It can also be thought as a graph obtained by deleting every alternate rim edge of . Being a spanning subgraph of strongly prime graph
. Being a spanning subgraph of strongly prime graph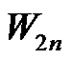 ,
, 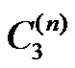 is a strongly prime graph.
is a strongly prime graph.
Corollary 3.13: The star 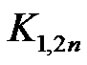 is a strongly prime graph.
is a strongly prime graph.
Proof: 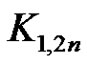 is obtained from strongly prime graph
is obtained from strongly prime graph 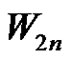 by deleting all the rim edges of the
by deleting all the rim edges of the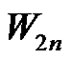 . Being a spanning subgraph of strongly prime graph
. Being a spanning subgraph of strongly prime graph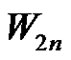 ,
, 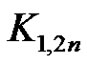 is a strongly prime graph.
is a strongly prime graph.
4. Concluding Remarks
The prime numbers and their behaviour are of great importance as prime numbers are scattered and there are arbitrarily large gaps in the sequence of prime numbers. If these characteristics are studied in the frame work of graph theory then it is more challenging and exciting as well.
Here we investigate several results on prime graphs. This discussion becomes more interesting in the situation when two vertices of a graph are identified. We also introduce a concept of strongly prime graph. As every prime graph is not a strongly prime graph it is very exciting to investigate graph families which are strongly prime graphs. We investigate several classes of prime graph which are strongly prime graph.
5. Acknowledgements
The authors are highly thankful to the anonymous referee for valuable comments and constructive suggestions.
REFERENCES
- J. Gross and J. Yellen, “Graph Theory and Its Applications,” CRC Press, Boca Raton, 1999.
- D. M. Burton, “Elementary Number Theory,” 2nd Edition, Brown Publishers, New York, 1990.
- J. A. Gallian, “A Dynamic Survey of Graph Labeling,” The Electronic Journal of Combinatorics, Vol. 18, 2011. http://www.combinatorics.org/Surveys/ds6.pdf
- A. Tout, A. N. Dabboucy and K. Howalla, “Prime Labeling of Graphs,” National Academy Science Letters, Vol. 11, 1982, pp. 365-368.
- H. L. Fu and K. C. Huang, “On Prime Labellings,” Discrete Mathematics, Vol. 127, No. 1-3, 1994, pp. 181-186. doi:10.1016/0012-365X(92)00477-9
- S. M. Lee, I. Wui and J. Yeh, “On the Amalgamation of Prime Graphs,” Bulletin of the Malaysian Mathematical Sciences Society (Second Series), Vol. 11, 1988, pp. 59-67.
- T. Deretsky, S. M. Lee and J. Mitchem, “On Vertex Prime Labelings of Graphs,” In: J. Alvi, G. Chartrand, O. Oellerman, A. Schwenk, Eds., Graph Theory, Combinatorics and Applications: Proceedings of the 6th International Conference Theory and Applications of Graphs, Wiley, New York, 1991, pp. 359-369.
- S. K. Vaidya and K. K. Kanani, “Prime Labeling for Some Cycle Related Graphs,” Journal of Mathematics Research, Vol. 2, No. 2, 2010, pp. 98-103. http://ccsenet.org/journal/index.php/jmr/article/view/4423/ 4743
- S. K. Vaidya and U. M. Prajapati, “Some Switching Invariant Prime Graphs,” Open Journal of Discrete Mathematics, Vol. 2, No. 1, 2012, pp. 17-20. doi:10.4236/ojdm.2012.21004
- S. K. Vaidya and U. M. Prajapati, “Some Results on Prime and k-Prime Labeling,” Journal of Mathematics Research, Vol. 3, No. 1, 2011, pp. 66-75. http://ccsenet.org/journal/index.php/jmr/article/download/ 7881/6696
- M. A. Seoud and M. Z. Youssef, “On Prime Labeling of Graphs,” Congressus Numerantium, Vol. 141, 1999, pp. 203-215.