Open Journal of Discrete Mathematics
Vol. 2 No. 1 (2012) , Article ID: 17156 , 3 pages DOI:10.4236/ojdm.2012.21005
On Cycle Related Graphs with Constant Metric Dimension
1Department of Mathematics, FAST-National University of Computer and Emerging Sciences, Peshawar, Pakistan
2Centre for Advanced Studies in Pure and Applied Mathematics, Bahauddin Zakariya University, Multan, Pakistan
Email: *gohar.ali@nu.edu.pk
Received September 16, 2011; revised November 2, 2011; accepted December 7, 2011
Keywords: Metric dimension; basis; resolving set; dragon graph
ABSTRACT
If 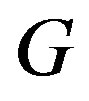 is a connected graph, the distance
is a connected graph, the distance 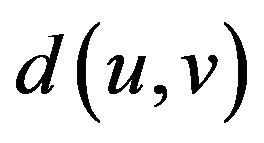 between two vertices
between two vertices 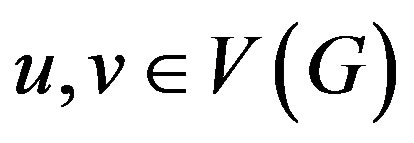 is the length of a shortest path between them. Let
is the length of a shortest path between them. Let 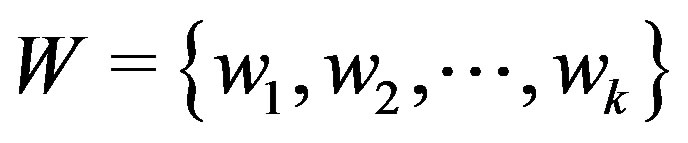 be an ordered set of vertices of
be an ordered set of vertices of  and let
and let  be a vertex of
be a vertex of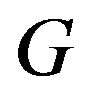 . The representation
. The representation 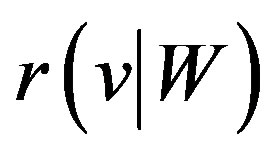 of
of 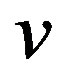 with respect to
with respect to 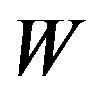 is the
is the  -tuple
-tuple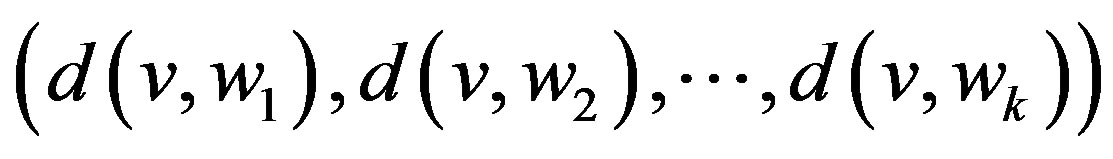 . If distinct vertices of
. If distinct vertices of 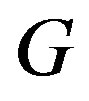 have distinct representations with respect to
have distinct representations with respect to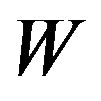 , then
, then 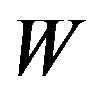 is called a resolving set or locating set for
is called a resolving set or locating set for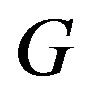 . A resolving set of minimum cardinality is called a basis for
. A resolving set of minimum cardinality is called a basis for 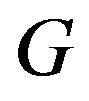 and this cardinality is the metric dimension of
and this cardinality is the metric dimension of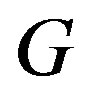 , denoted by
, denoted by . A family
. A family  of connected graphs is a family with constant metric dimension if
of connected graphs is a family with constant metric dimension if 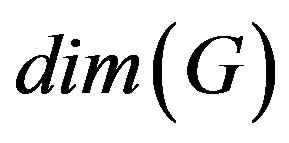 is finite and does not depend upon the choice of
is finite and does not depend upon the choice of  in
in . In this paper, we show that dragon graph denoted by
. In this paper, we show that dragon graph denoted by 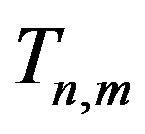 and the graph obtained from prism denoted by
and the graph obtained from prism denoted by 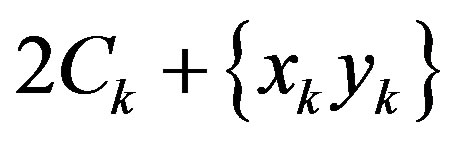 have constant metric dimension.
have constant metric dimension.
1. Notation and Preliminary Results
If 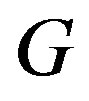 is a connected graph, the distance
is a connected graph, the distance 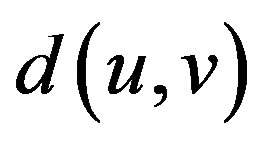 between two vertices
between two vertices  is the length of a shortest path between them. Let
is the length of a shortest path between them. Let  be an ordered set of vertices of
be an ordered set of vertices of  and let
and let 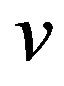 be a vertex of
be a vertex of . The representation of the
. The representation of the 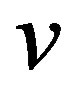 with respect to
with respect to  is denoted by
is denoted by 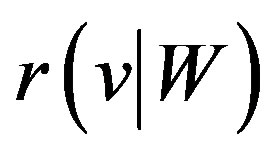 is the
is the
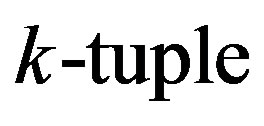 . If distinct vertices of
. If distinct vertices of  have distinct representations with respect to
have distinct representations with respect to , then
, then 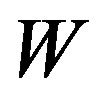 is called a resolving set or locating set for
is called a resolving set or locating set for 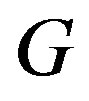 [1]. A resolving set of minimum cardinality is called a metric basis for
[1]. A resolving set of minimum cardinality is called a metric basis for 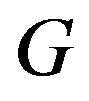 and its cardinality is the metric dimension of
and its cardinality is the metric dimension of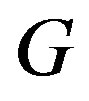 , denoted by
, denoted by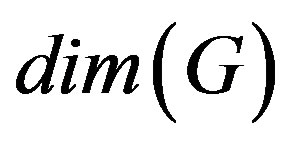 . The concepts of resolving set and metric basis have previously appeared in the literature (see [1-14]).
. The concepts of resolving set and metric basis have previously appeared in the literature (see [1-14]).
For a given ordered set of vertices  of a graph
of a graph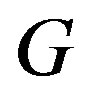 , the ith component of
, the ith component of 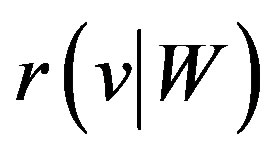 is 0 f and only if
is 0 f and only if . Thus, to show that
. Thus, to show that 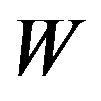 is a resolving set it sufficient to verify that
is a resolving set it sufficient to verify that 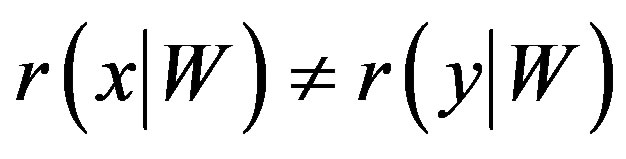 for each pair of distinct vertices
for each pair of distinct vertices  .
.
Motivated by the problem of uniquely determining the location of an intruder in a network, the concept of metric dimension was introduced by Slater in [2] and studied independently by Harary et al. [3]. Applications of this invariant to the navigation of robots in networks are discussed in [4] and applications to chemistry in [1] while applications to problems of pattern recognition and image processing, some of which involve the use of hierarchical data structures are given in [5].
By denoting 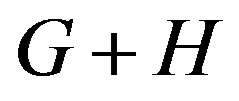 the join of
the join of  and
and , a
, a 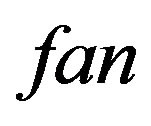 is
is  for
for 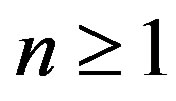 and
and 
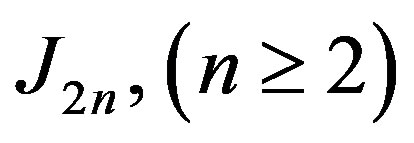 (also known as
(also known as ) is obtained from the
) is obtained from the 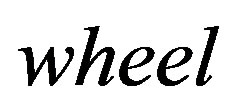
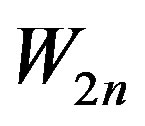 by alternately deleting
by alternately deleting 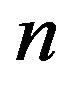 spokes. Caceres et al. [6] found the metric dimension of fan
spokes. Caceres et al. [6] found the metric dimension of fan 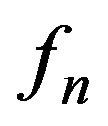 and Tomescu et al. [7] found the metric dimension of
and Tomescu et al. [7] found the metric dimension of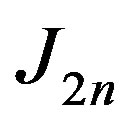
 . Also Tomescu et al. [8] the partition and connected dimension of wheels.
. Also Tomescu et al. [8] the partition and connected dimension of wheels.
Chartrand et al. proved:
Theorem 1: [1] A graph 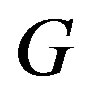 has metric dimension
has metric dimension 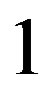 if and only if
if and only if 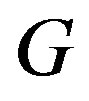 is a path.
is a path.
Hence paths on 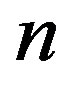 vertices constitute a family of graphs with constant metric dimension. Similarly, cycles with
vertices constitute a family of graphs with constant metric dimension. Similarly, cycles with  vertices also constitute such a family of graphs as their metric dimension is 2. Since
vertices also constitute such a family of graphs as their metric dimension is 2. Since 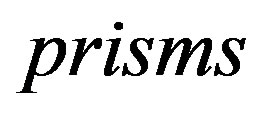
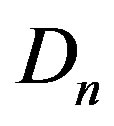 are the trivalent plane graphs obtained by the cartesian product of the path
are the trivalent plane graphs obtained by the cartesian product of the path 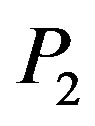 with a cycle
with a cycle , hence they constitute a family of
, hence they constitute a family of  -
-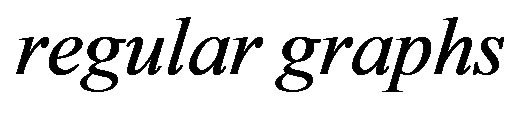 with constant metric dimension. Also Javaid et al. proved in [9] that the plane graph
with constant metric dimension. Also Javaid et al. proved in [9] that the plane graph 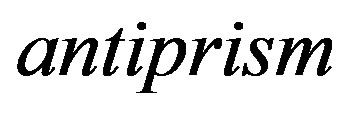
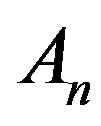 constitutes a family of regular graphs with constant metric dimension as
constitutes a family of regular graphs with constant metric dimension as 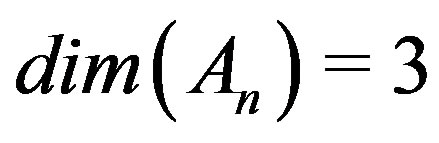 for every
for every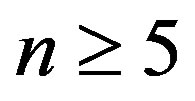 .
.
Let 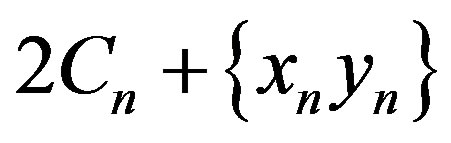 be a family of graphs of order
be a family of graphs of order 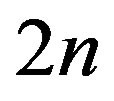 obtained from a prism
obtained from a prism 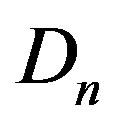 as shown in Figure 1 and Figure 2 respectively, by deleting the spokes
as shown in Figure 1 and Figure 2 respectively, by deleting the spokes 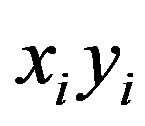 for
for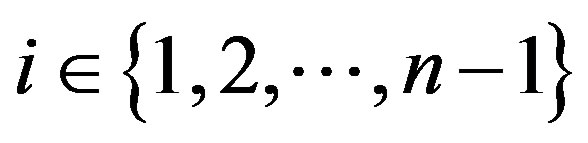 . We prove the following.
. We prove the following.
Theorem 2: Let  with
with 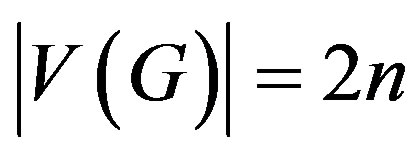 , then
, then 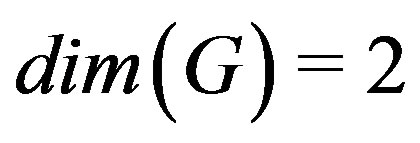 for
for .
.
Let 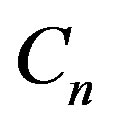 be a cycle with vertex set
be a cycle with vertex set 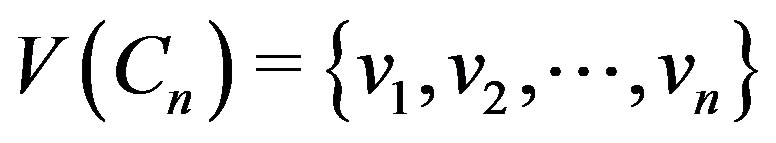 and
and 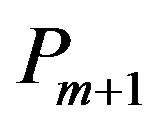 be a path with vertex set
be a path with vertex set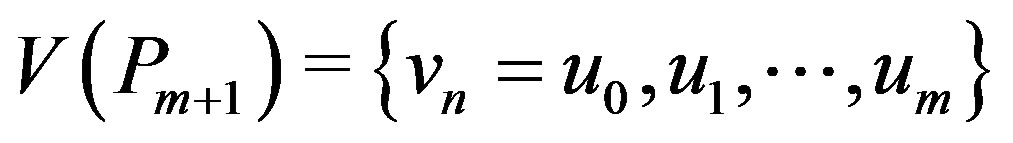 . Dragon graph
. Dragon graph  as shown in Figure 3, is a graph of order
as shown in Figure 3, is a graph of order 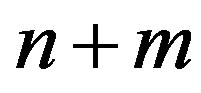 obtained by identifying
obtained by identifying  of
of  with
with 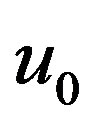 of
of . We prove the following.
. We prove the following.
Theorem 3: For all 
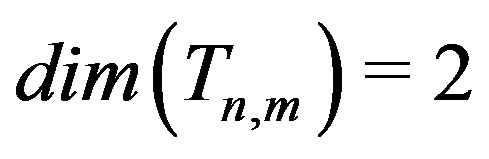 .
.
2. Proofs
Proof of the Theorem 2: By Theorem 1,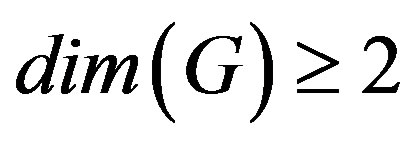 . We only need to show that
. We only need to show that 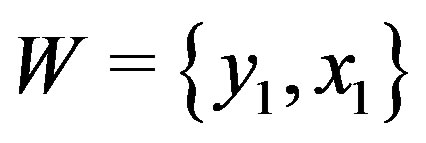 is a resolving set for
is a resolving set for , which is obviously of minimal cardinality.
, which is obviously of minimal cardinality.

Figure 1. Prism Dn.
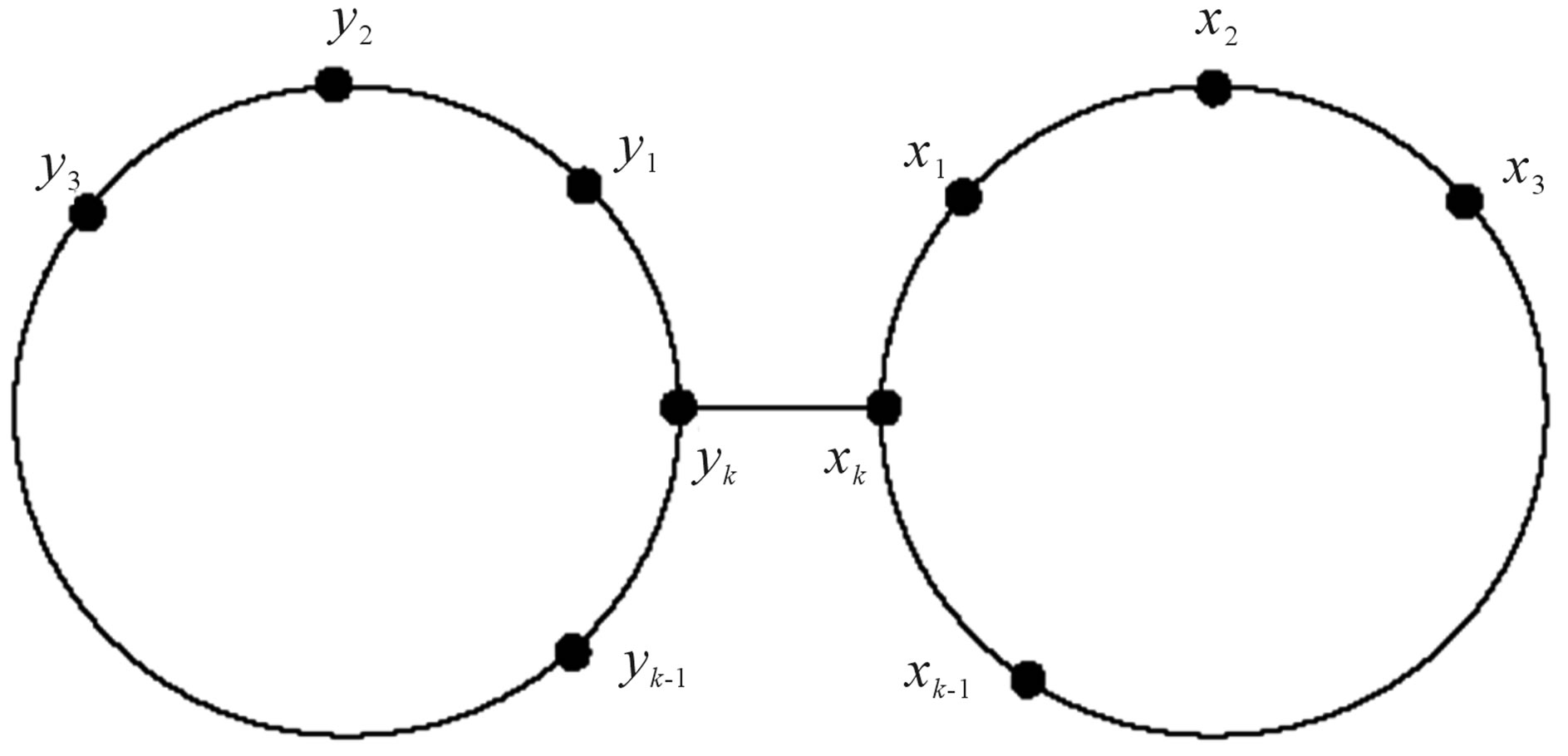
Figure 2. Graph 2Ck + {xk yk}.
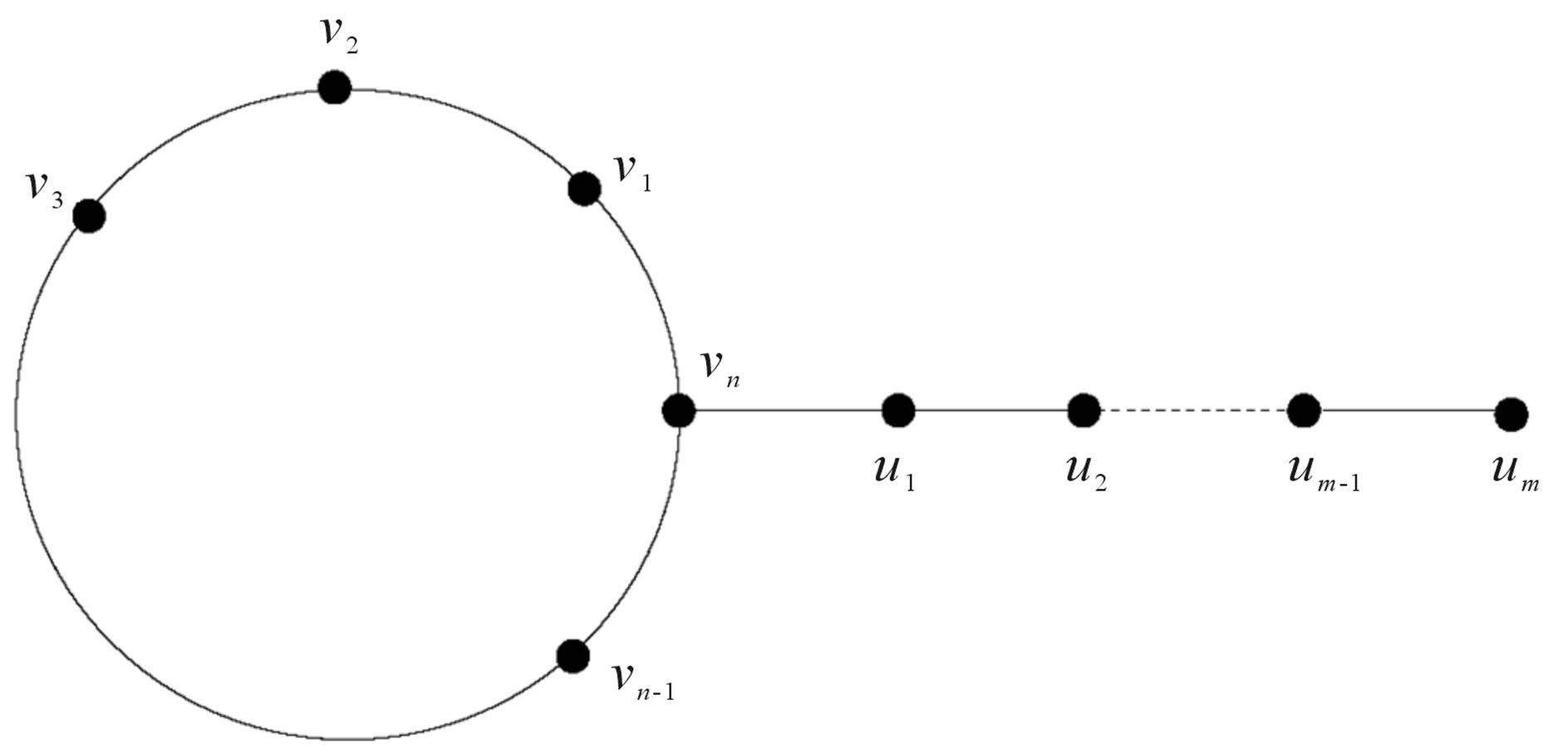
Figure 3. Dragon graph.
Case (a) When 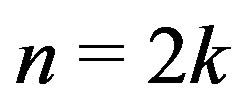 for
for 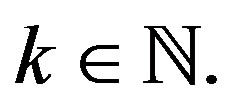 Representations of all vertices from
Representations of all vertices from 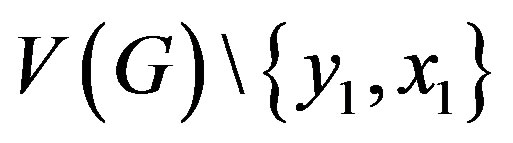 are as follows,
are as follows,
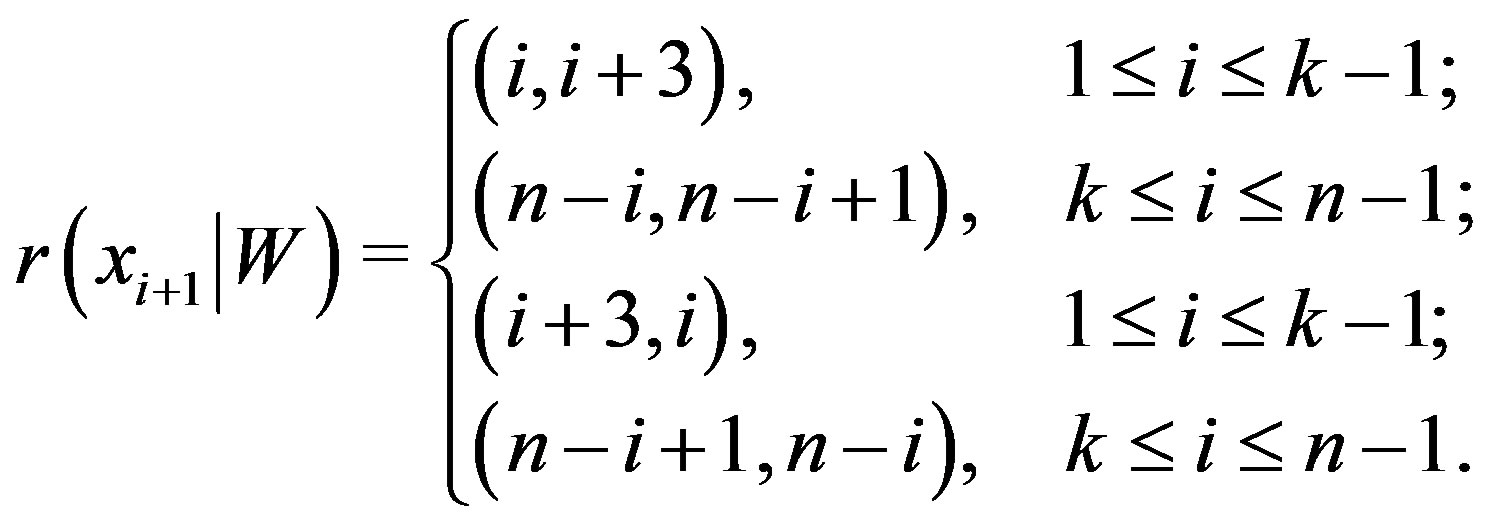
It is easy to check that all the above representations are distinct. For example, suppose that 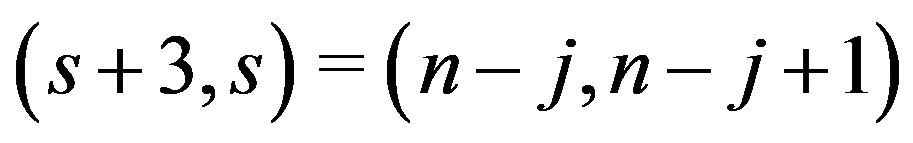 for some fixed
for some fixed 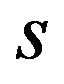 and
and . Then
. Then 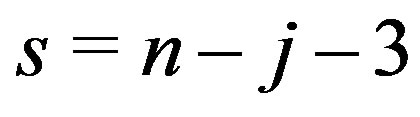 and
and , a contradiction.
, a contradiction.
Case (b) When 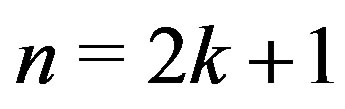 for
for  Representations of vertices from
Representations of vertices from 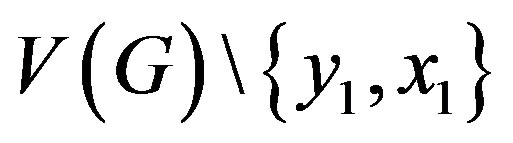 are as follows,
are as follows,
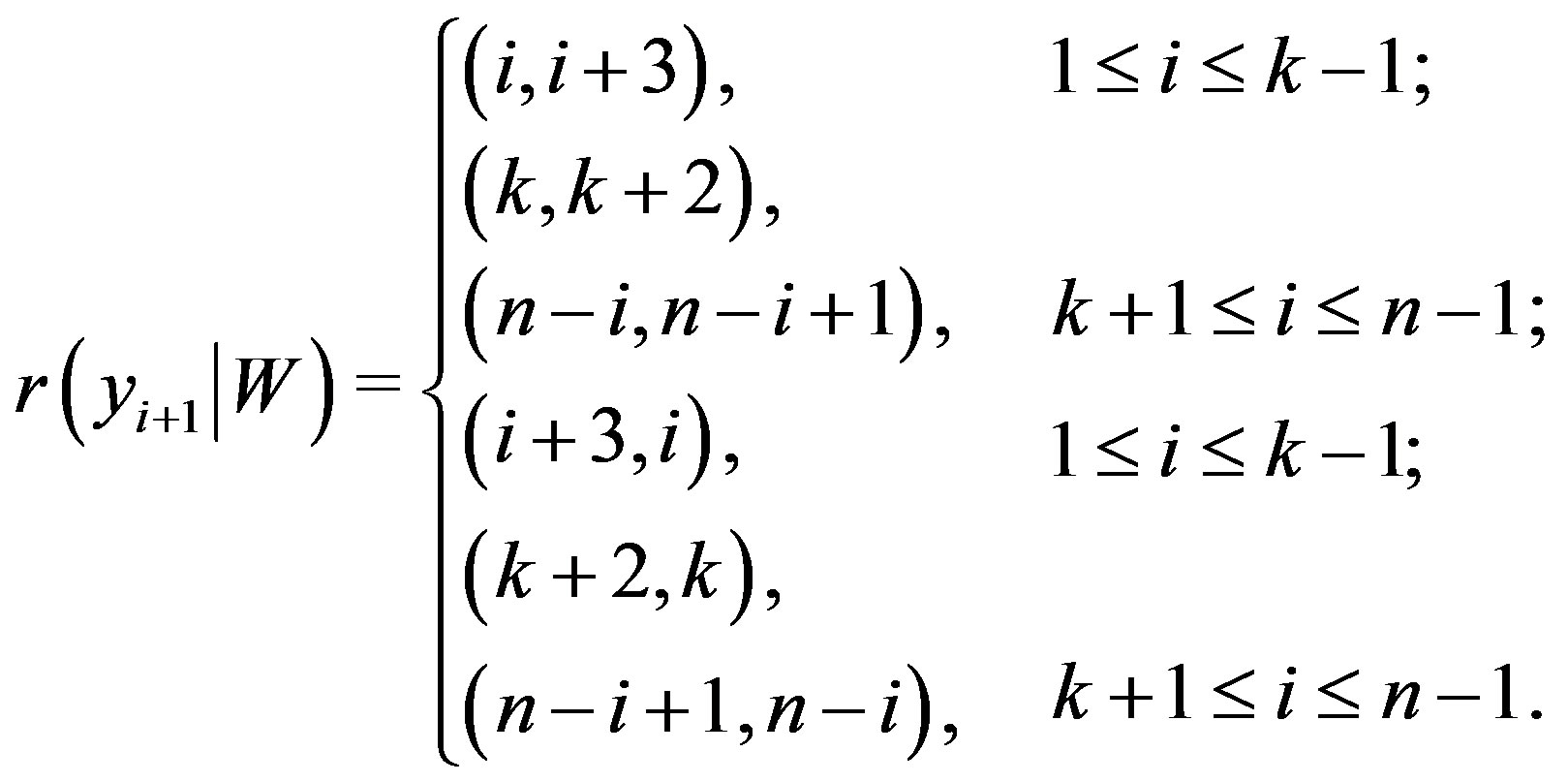
All the above representations are also distinct.
Proof of the Theorem 3: By Theorem 1, 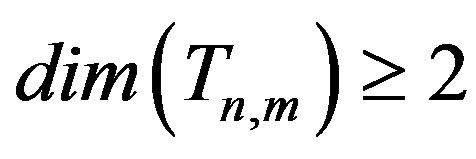 . We only need to show that there is a resolving set
. We only need to show that there is a resolving set  of cardinality 2.
of cardinality 2.
Case (a) When 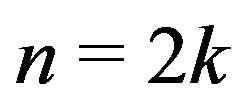 for
for 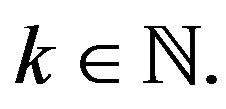 The set
The set 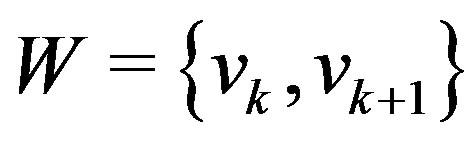 is a resolving set for the graph
is a resolving set for the graph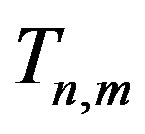 . Representations of all vertices from
. Representations of all vertices from 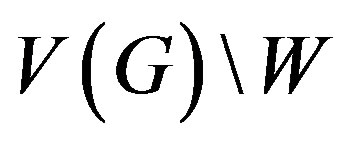 are as follows,
are as follows,
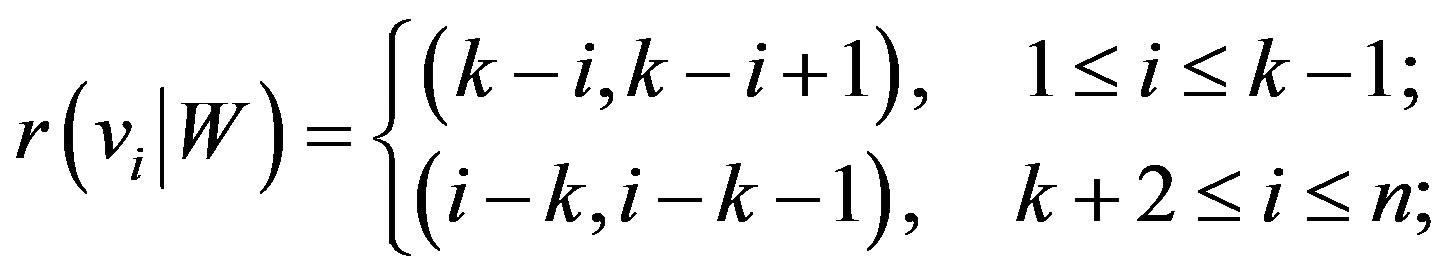
and
 ,
, 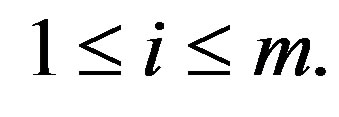
It is easy to check that all the representations are distinct. For example, suppose that  for some fixed s and j. Then
for some fixed s and j. Then 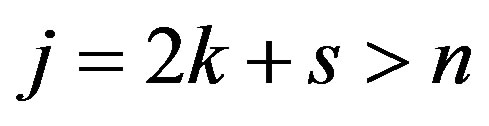 because
because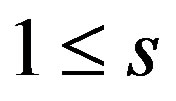 , a contradiction.
, a contradiction.
Case (b) When 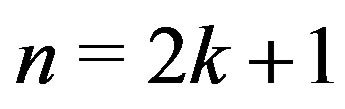 for
for 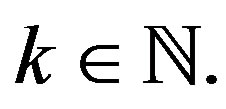 The set
The set 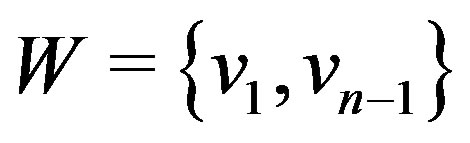 is a resolving set for the graph
is a resolving set for the graph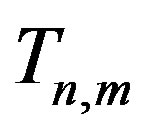 . Representations of all vertices from
. Representations of all vertices from 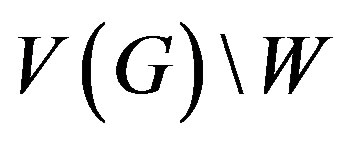 are as follows,
are as follows,
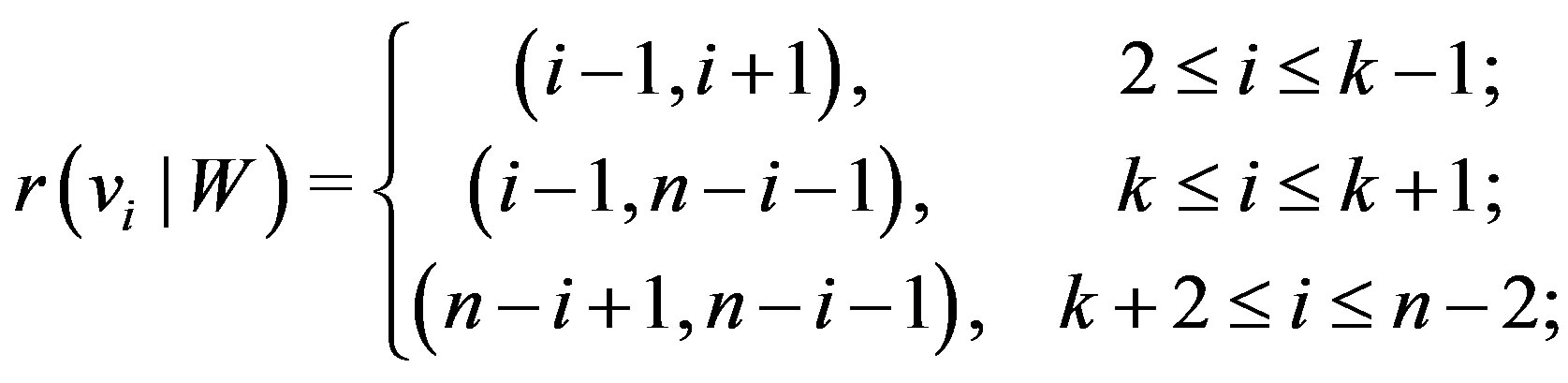
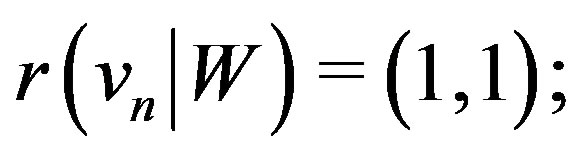
and
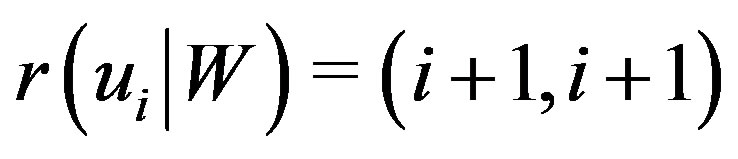 ,
, 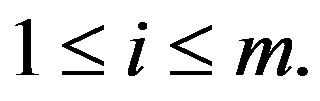
All the above representations are distinct.
3. Acknowledgements
This research is partially supported by FAST-National University of Computer and Emerging Sciences, Peshawar, Bahauddin Zakariya University, Multan and Higher Education Commission of Pakistan.
REFERENCES
- J. Caceres, C. Hernando, M. Mora, I. M. Pelayo, M. L. Puertas, C. Seara and D. R. Wood, “On the Metric Dimension of Some Families of Graphs,” Electronic Notes in Discrete Mathematics, Vol. 22, 2005, pp. 129- 133.
- G. Chartrand, L. Eroh, M. A. Johnson and O. R. Oellermann, “Resolvability in Graphs and Metric Dimension of a Graph,” Discrete Applied Mathematics, Vol. 105, 2000, pp. 99-113. doi:10.1016/S0166-218X(00)00198-0
- F. Harary and R. A. Melter, “On the Metric Dimension of a Graph,” Ars Combinatoria, Vol. 2, 1976, pp. 191-195.
- I. Javaid, M. T. Rahim and K. Ali, “Families of Regular Graphs with Constant Metric Dimension,” Utilitas Mathematica, Vol. 75, 2008, pp. 21-33.
- S. Khuller, B. Raghavachari and A. Rosenfeld, “Localization in Graphs,” Technical Report CS-TR-3326, University of Maryland at College Park, 1994.
- R. A. Melter and I. Tomescu, “Metric Bases in Digital Geometry,” Computer Vision, Graphics, and Image Processing, Vol. 25, No. 1, 1984, pp. 113-121. doi:10.1016/0734-189X(84)90051-3
- P. J. Slater, “Dominating and Reference Sets in Graphs,” Journal of Mathematical Physics, Vol. 22, 1998, pp. 445-455.
- I. Tomescu and I. Javaid, “On the Metric Dimension of the Jahangir Graph,” Bulletin Mathématique de la Société des Sciences. Mathématiques de Roumanie, Vol. 50, No. 4, 2007, pp. 371-376.
- K. Karliraj and V. J. Vernold, “On Equatable Coloring of Helm and Gear Graphs,” International Journal of Mathematical Combinatorics, Vol. 4, No. 1, 2010, pp. 32-37.
- I. Javaid, “On the Connected Partition Dimension of Unicyclic Graphs,” Journal of Combinatorial Mathematics and Combinatorial, Vol. 65, 2008, pp. 71-77.
- I. Javaid and S. Shokat, “On the Patition Dimension of Some Wheel Related Graph,” Journal of Prime Research in Mathematics,Vol. 4, 2008, pp. 154-164.
- M. Ali, M. Imran, A. Q. Baig, M. K. Shafiq and G. Ali, “On the Metric Dimension of Mobius Ladders,” Ars Combinatoria, in press.
- I. Tomescu, I. Javaid, et al., “On the Patition Dimension and Connected Partition Dimension Wheels,” Ars Combinatoria, Vol. 84, 2007, pp. 311-317.
- I. Javaid, et al., “Fault-Tolerance in Resolvibility,” Utilitas Mathematica, Vol. 80, 2009, pp. 263-275.
NOTES
*Corresponding author.

