Optics and Photonics Journal
Vol.3 No.4(2013), Article ID:35628,4 pages DOI:10.4236/opj.2013.34045
Influences of the Shape of Rods in Two Dimension Photonic Crystals on Their Defect Eigenmodes
School of Science, Xi’an Jiaotong University, Xi’an, China
Email: *xiaogh@mail.xjtu.edu.cn
Copyright © 2013 Guo-Hong Xiao, Li-Qing Huang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received Febuary 28, 2013; revised April 5, 2013; accepted June 3, 2013
Keywords: Photonic Crystal; Structure Parameter; Defect Eigenmode; Rod Shape
ABSTRACT
The cross section of photonic crystal fiber (PCF) is a two dimensional photonic crystal. The rods formed in PCF are not exact cylinders, the shape of rods will affect the eigenmode formed in two dimensional photonic crystals around a defect. Based on the relations between the defect eigenmodes and the radius of dielectric cylinders, the defect eigenmodes in photonic crystals in which the ellipse rods take the place of cylinders are studied by numerical calculation. The analysis of the relation between the eigenfrequency and the minor axis radius of ellipse rods show that the defect eigenfrequency is controlled by the cross section area of rods and the distribution of electromagnetic field around the defect is also affected by the cross section shape of rods. It provides a better way to modify the distribution of electromagnetic fields in photonic crystal and keeps the eigenfrequency unchanged.
1. Introduction
More than a decade after the concept of photonic crystal, Photonic Crystal Fibers (PCF) is now a proven technology that is competing with conventional fibers in many applications. The emergence of localized defect modes in the gap frequency region when a disorder is introduced to the periodic dielectric structure is one of the most important properties of photonic crystals. There are usually two types of two dimension (2D) structure which are adopted in PFC, triangular lattice and square lattice of dielectric cylinders. In order to form a defect, one or more cylinders are moved from a regular lattice structure, as shown in Figure 1. The localized defect mode will appear
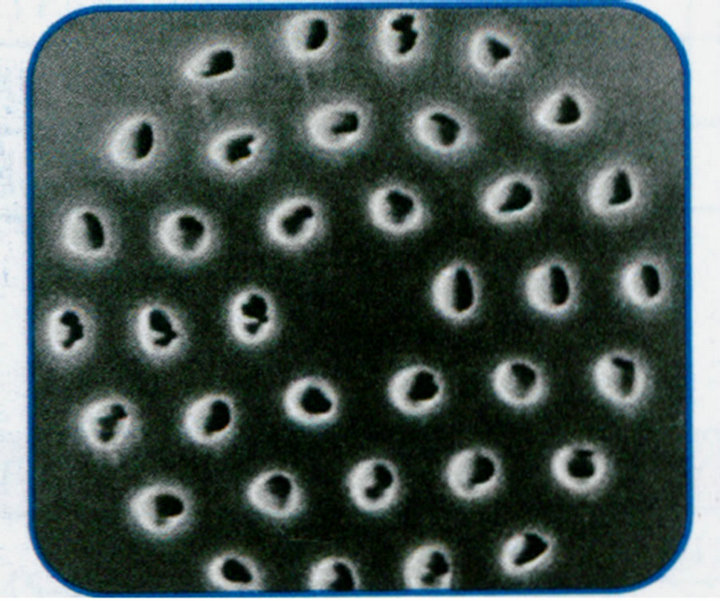
Figure 1. SEM of a Cross section of a solid core photonic crystal fiber.
around the defect, which is called an eigenmode. The relations between the eigenmode or bandgaps and the structure parameters are studied extensively [1,2].
However the dielectric rods fabricated with recent technology in PCF are not exact cylinders, as shown in Figure 1. How the shapes of rods affect the eigenmode in PCF will be investigated in this paper. The result will show the key factor for fabrication process of PCF.
2. Modeling of 2D Defected Photonic Crystals with Ellipse Rods and Numerical Analysis
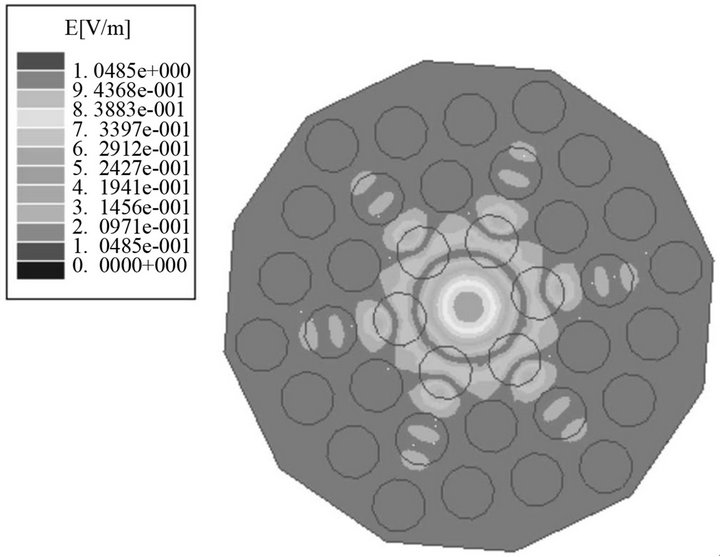
The 2D photonic crystals in the form of triangular lattice and square lattice of circular dielectric cylinders have complete bandgaps for TM modes. A localized eigenmode will form around a defect as shown in Figure 2.
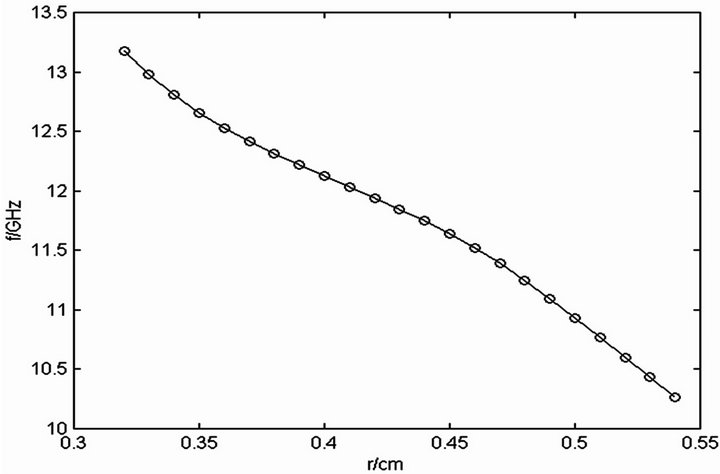
The relations between the eigenfrequency and the radius of dielectric cylinders in a small region have been calculated numerically with Finite Element Method [3,4], and are shown in Figure 3. The eigenfrequency of the localized defect mode decreases roughly linearly with the increase of the radius. As the rods fabricated in 2D photonic crystals are not exact cylinders, the shape of rods will affect the bandgaps [5] and the defect eigemodes. The ellipse rods are taken to simulate the rods with ir-
 (a)
(a)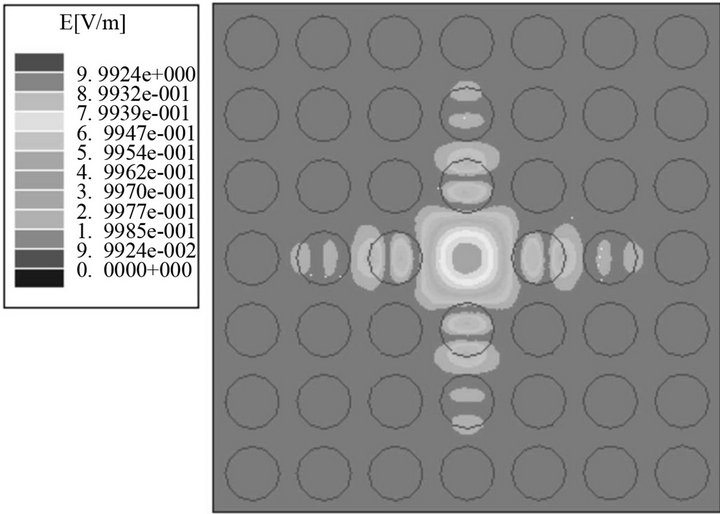 (b)
(b)
Figure 2. A localized defect eigenmode in 2D photonic crystals with dielectric cylinders, lattice constant is 1.27 cm, radius of cylinders is 0.48 cm, dielectric constant of cylinders is 9, the background is vacuum. (a) Triangular lattice, the eigenfrequency is 11.2466 GHz; (b) Square lattice, the eigenfrequency is 11.1244 GHz.
 (a)
(a)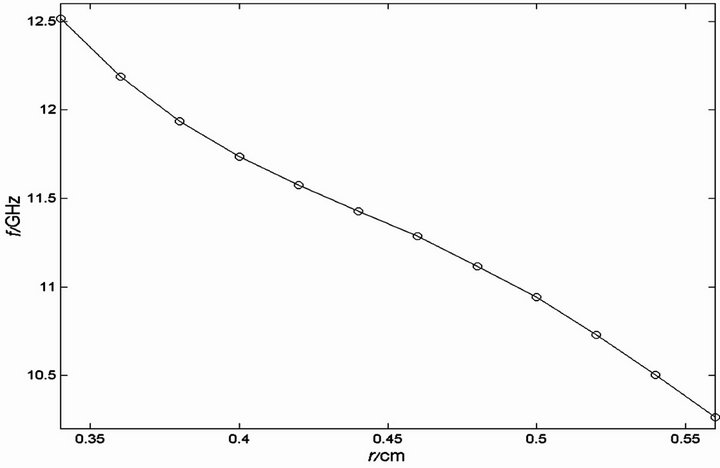 (b)
(b)
Figure 3. The relations between the eigenfrequencies and the radii of dielectric cylinders. (a) Triangular lattice; (b) Square lattice.
regular shapes for studying the eigenmodes.
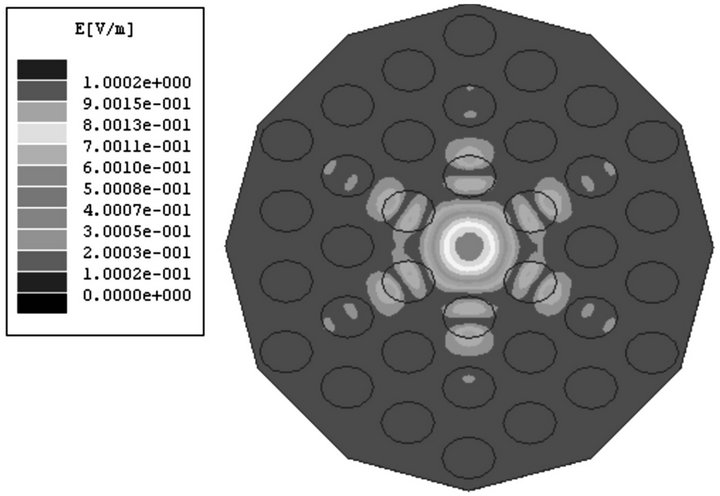
As for the triangular lattice structure shown in Figure 2(a), if the radius of cylinders becomes smaller in horizontal or vertical direction in a small range, i.e. the ellipse rods take the place of cylinders, the localized defect eigenmodes can also form in the two structures as shown in Figure 4. Obviously the two structures have different symmetry.
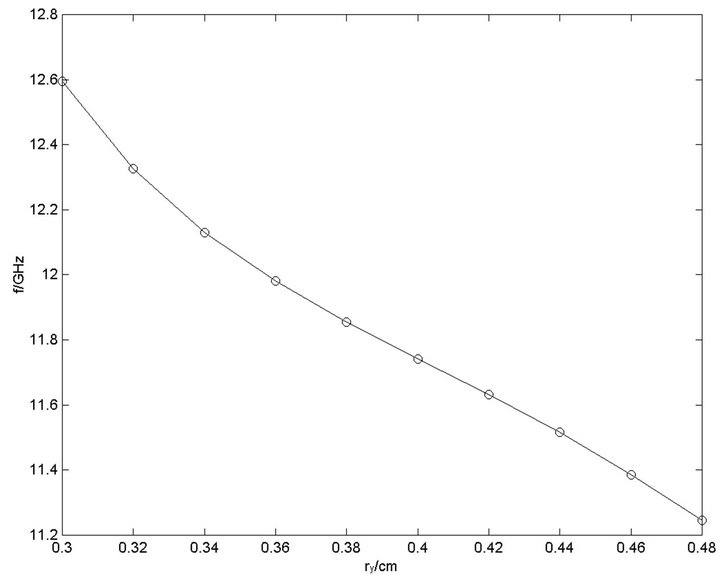
And the distributions of the magnitude of electric field in the two structures are also different. But the numerical calculated result shows that they have almost same eigenfrequency. We calculate the eigenfrequencies of the two structures with different minor axis radii. Their relations are shown in Figure 5. They are almost same. This result means that the eigenfrequency is independent of the direction of the minor axis.
In order to make sure of this conclusion, we let the minor axis have different directions in a triangular lattice structure as shown in Figure 6. The eigenfrequency almost keeps unchanged, and the symmetry of the distribution of the electric field in this structure is disturbed. A natural explanation to the common eigenfrequency is that they have a common cross section area of rods. The cross section area of these ellipse rods is
 (a)
(a)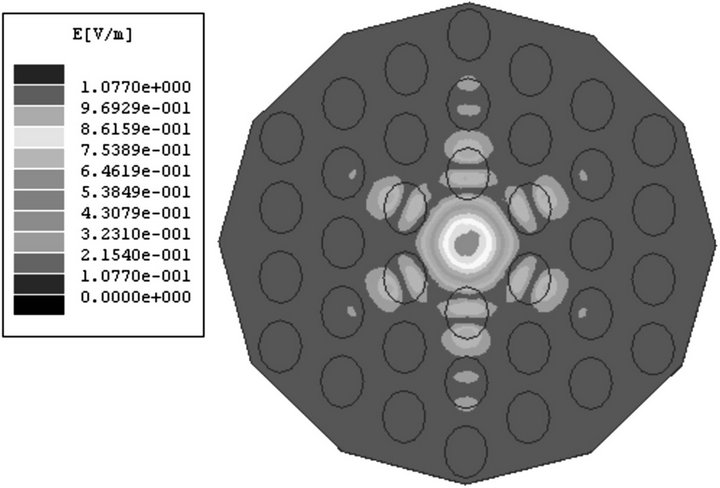 (b)
(b)
Figure 4. The distribution of electric field in 2D triangular lattice photonic crystals with ellipse rods. (a) Minor axis of ellipse rods is along the vertical direction.  cm
cm 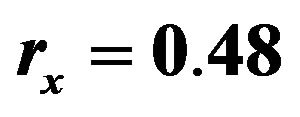 cm, the eigenfrequency is 11.8542 GHz; (b) Minor axis of ellipse rods is along the horizontal direction.
cm, the eigenfrequency is 11.8542 GHz; (b) Minor axis of ellipse rods is along the horizontal direction. 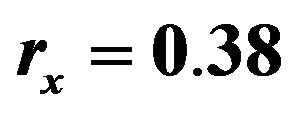 cm
cm 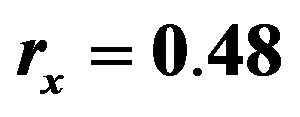 cm, the eigenfrequency is 11.8671 GHz
cm, the eigenfrequency is 11.8671 GHz
 (a)
(a)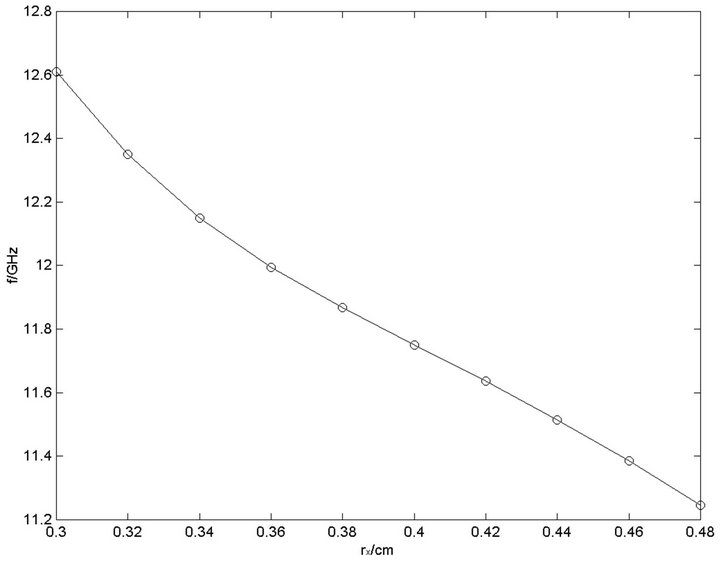 (b)
(b)
Figure 5. The relations between the eigenfrequencies and the minor axis radii of ellipse rods. (a) The minor axis of ellipse rods is along the vertical direction; (b) The minor axis of ellipse rods is along the horizontal direction.
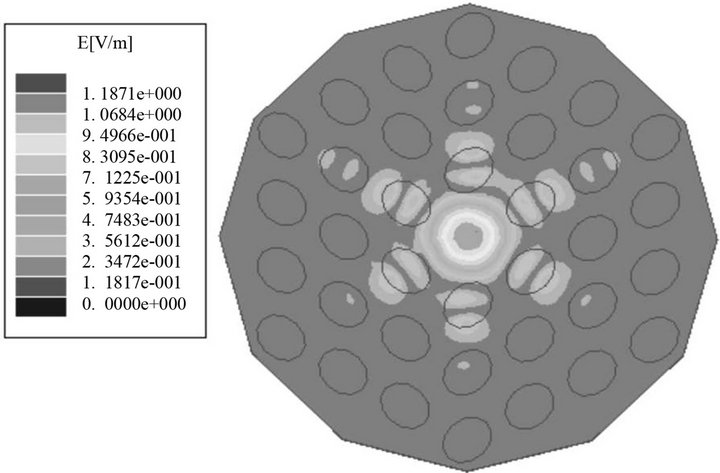
Figure 6. The distribution of electric field in 2D triangular lattice photonic crystal, the minor axis of ellipse rods have different directions. The eigenfrequency is 11.8611 GHz.
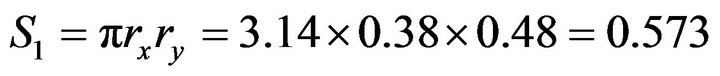 cm2 (1)
cm2 (1)
In Figure 3(a) when the eigenfrequency is 11.8611 GHz, the corresponding radius of cylinders equals 0.429 cm. The cross section area of these cylinders is
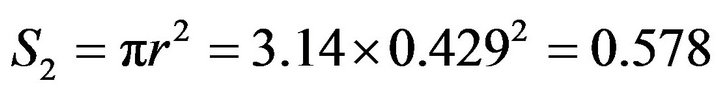 cm2 (2)
cm2 (2)
It is almost same to the cross section area of ellipse rods.
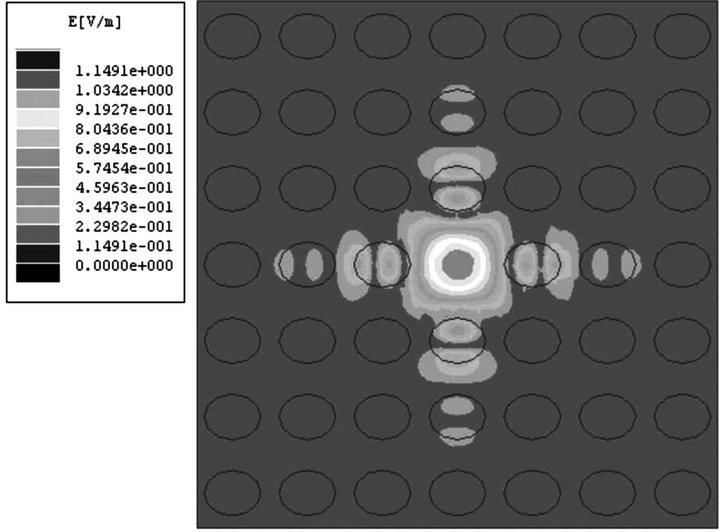
As for the square lattice structure, it shows the same conclusion. Figure 7 shows the distribution of the electric field in these structures with ellipse rods. Although the directions of minor axis of ellipse rods are different, they almost have same eigenfrequency. The cross section area of these rods is also 0.573 cm2. In Figure 3(b) when the eigenfrequency is 11.5210 GHz, the radius of dielectric cylinders equals 0.428 cm. The corresponding cross section area is 0.575 cm2. If we make a further change to the shape of these rods, i.e. the cross section shape of rods is square, and keeps their area equal 0.574 cm2 as shown in Figure 8. Its eigenfrequency numerically calculated is 11.4663 GHz. The relative change of the eigenfrequency is only 0.5%.
3. Conclusion
From the numerically calculated results above, it is clear that the eigenfrequency of defect eigenmodes formed in 2D defect photonic crystals is controlled by the cross section area of rods, and the distribution of electromagnetic field around the defect is affected by the cross section shape of rods. As the localized defect in PCF acts as a resonant cavity. The resonant eigenfrequency is determined by the cavity space which is surrounded by the
 (a)
(a)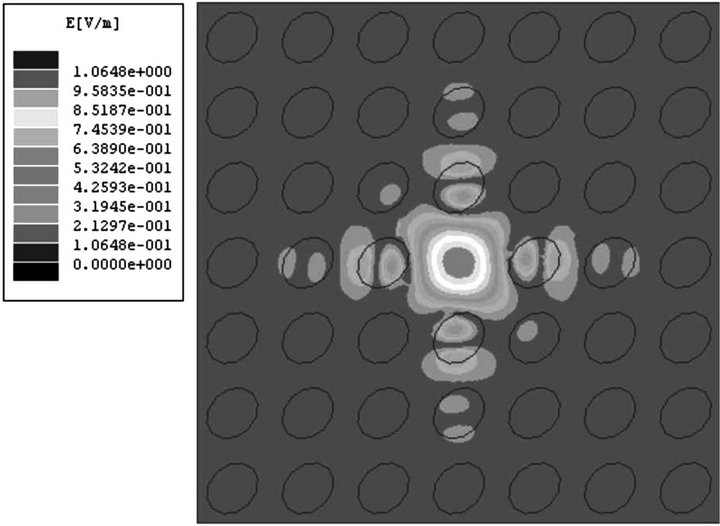 (b)
(b)
Figure 7. The distributions of electric field in 2D square lattice photonic crystals with ellipse rods. The minor axis radius is 0.38 cm, the major axis radius is 0.48 cm. (a) The eigenfrequency is 11.5210 GHz; (b) The eigenfrequency is 11.5508 GHz.
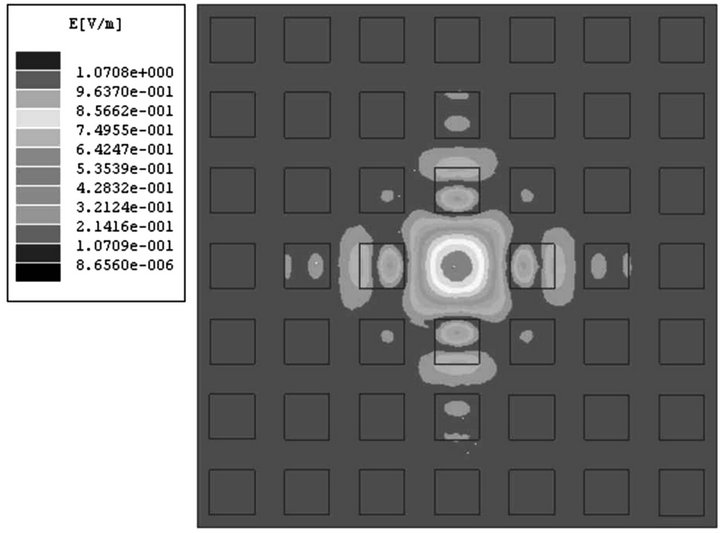
Figure 8. The distribution of the electric field in square lattice structure with square rods. The cross section area of rods is 0.574 cm2. The eigenfrequency is 11.4663 GHz.
rods. And every rod is a scattering unit which direction of the minor axis determines the distributions of the field.
It is also clear to keep rods’ cross section area same is more important in fabrication process of PCF. From the results above we can modify the distribution of the electromagnetic field of eigenmodes around the defect in photonic crystals as keeping the eigenfrequency unchanged. It is an effective way to enhance the coupling of electromagnetic field with matter in some place of photonic crystals, and the electromagnetic energy could be used more effectively.
REFERENCES
- K. Sakoda, “Optical Properties of Photonic Crystals,” Springer, New York, 2004, p. 125
- X. H. Cai, W. H. Zheng, X. T. Ma, G. Ren and J. B. Xia, “Photonic Band Structures of Two-Dimensional Photonic Crystals with Deformed Lattices,” Chinese Physics, Vol. 14, No. 12, 2005, p. 2507. doi:10.1088/1009-1963/14/12/023
- G.-H. Xiao, et al., “Influences of Structure Parameters of Triangular Lattice Photonic with Defect on Eigen Mode,” Acta Photonica Sinica, Vol. 37, No. 4, 2006, p. 725.
- G.-H. Xiao, et al., “The Influences of the Structure Parameters of a Square Lattice Photonic Crystal with a Defect in It on Its Defect Mode,” Laser Journal, Vol. 28, No. 6, 2007, p. 27.
- F. Zhuang, L. Wu and S. L. He, “The Influences of the Structure Parameters of a Square Lattice Photonic Crystal with a Defect in It on Its Defect Mode,” Chinese Physics, Vol. 11, No. 8, 2002, Article ID: 0834.
NOTES
*Corresponding author.

