American Journal of Computational Mathematics
Vol.06 No.04(2016), Article ID:72912,21 pages
10.4236/ajcm.2016.64034

ADI Finite Element Method for 2D Nonlinear Time Fractional Reaction-Subdiffusion Equation

Peng Zhu1, Shenglan Xie2

1Department of Mathematics, Jiaxing University, Jiaxing, China

2Nanhu College, Jiaxing University, Jiaxing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

Received: October 18, 2016; Accepted: December 18, 2016; Published: December 21, 2016

ABSTRACT

In this paper, an alternating direction Galerkin finite element method is presented for solving 2D time fractional reaction sub-diffusion equation with nonlinear source term. Firstly, one order implicit-explicit method is used for time discretization, then Galerkin finite element method is adopted for spatial discretization and obtain a fully discrete linear system. Secondly, Galerkin alternating direction procedure for the system is derived by adding an extra term. Finally, the stability and convergence of the method are analyzed rigorously. Numerical results confirm the accuracy and efficiency of the proposed method.

Keywords:

Nonlinear Fractional Differential Equation, Alternating Direction Implicit Method, Finite Element Method, Riemann-Liouville Fractional Derivative

1. Introduction

In this paper, we consider the following two-dimensional nonlinear fractional reaction- subdiffusion equation

(1)

with boundary and initial conditions

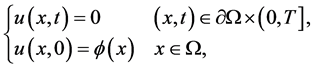(2)

where, , 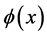is sufficiently smooth function. For simplicity, we assume coefficients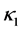, 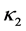and 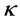are positive constants in this paper. In fact, our method and its corresponding theoretic result are also valid for variable coefficients. 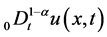is the Riemann-Liouville time fractional derivative of order defined by [1]

(3)

where 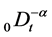denotes the Riemann-Liouville fractional integral operator defined as [1]

(4)

In addition, we assume that the nonlinear source term 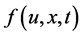satisfies the Lipschitz condition with respect to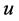, i.e., there exists a positive constant 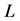such that

Problem (1) can be considered as a model for reaction-diffusion phenomena with anomalous diffusion, which has been widely applied in various fields of science and engineering. Generally, solutions of (1) can’t be obtained by analytical approach. So, there are various numerical methods developed for solving (1). Li and Ding [2] proposed higher order finite difference methods for solving 1D linear reaction and anomalous- diffusion equations. Zhuang, Liu and Anh, et al. [3] presented an implicit finite element method for solving 1D nonlinear fractional reaction-subdiffusion process. Dehghan, Abbaszadeh and Mohebbi [4] analyzed a meshless Galerkin method with radial basis functions of 2D linear fractional reaction-subdiffusion process. Yu, Jiang and Xu [5] derived an implicit compact finite difference scheme for solving 2D nonlinear fractional reaction-subdiffusion equation.

Alternating direction implicit (ADI) method was proposed by Peaceman, Rachford and Douglas [6] [7] [8] in 1950’s for multidimensional differential equations of integer order, which could reduce original multidimensional problem into a sequences of one- dimensional problems. Since the first ADI based finite difference (FD) scheme presented for 2D space fractional diffusion equation by Meerschaert, Scheffler and Tadjeran [9] , there are many literatures about various multidimensional fractional differential equations numerically solved by ADI technique. The following problem is always discussed:

(5)

where is Caputo fractional derivative of order defined as [1]

In the case of, Zhang and Sun [10] presented an ADI FE scheme and analyzed its stability and convergence property by energy method. Cui [11] constructed a compact ADI FD scheme and discussed its stability by Fourier method. In the case of, Zhang, Sun and Zhao [12] proposed a Crank-Nicolson compact ADI FD scheme, where stability and convergence property are also proved by energy method. Wang and Vong [13] presented another compact ADI FD scheme, where the original equation was first transformed into an equivalent form and then discretized by compact FD scheme combining with ADI technique. Li, Xu and Luo [14] presented an ADI finite element (FE) scheme for Equation (5), where stability and L2 error estimate are analyzed. ADI orthogonal spline collocation (OSC) scheme was developed by Fairweather, Yang and Xu, et al. [15] for solving Equation (5); stability and error estimate in various norms are given. The equivalent form of Equation (5) as following

(6)

is also often studied. For instances, Cui [16] presented a compact ADI FD scheme, where the local truncation error was analyzed and the stability was discussed by the Fourier method. Furthermore, the author analyzed the cause of low time accuracy when and gave a remedy. Zhang and Sun [17] proposed a Crank-Nicol- son compact ADI FD scheme for Equation (6), where stability and two error estimates are proved rigorously by energy method. Yao, Sun and Wu, et al. [18] first transformed Equation (6) into an equivalent form of Caputo fractional derivative and then derived a compact ADI FD scheme. Their numerical experiments show better numerical performance than the scheme in [16] . Compact ADI FD schemes were also derived for solving 2D/3D linear time fractional convection-diffusion equations [19] [20] [21] and 2D linear time fractional diffusion equations of distributed-order [22] [23] .

There are also lots of ADI based numerical methods for multidimensional space fractional differential equations. Fast iterative ADI FD schemes [24] [25] are designed for 2D/3D linear space fractional diffusion equations, which are first order accuracy in both time and space and have the advantage of low computational work and low memory storage. High order accurate ADI FD schemes are proposed for 2D linear space fractional diffusion equations [26] [27] and two-sided space fractional convection-dif- fusion equations [28] , which are based on weighted and shifted Grünwald operators or Lubich operators approximating Riemann-Liouville fractional derivatives respectively. Spectral direction splitting methods [29] are derived for 2D space fractional differential equations. Semi-implicit alternating direction FD scheme [30] and ADI FE scheme [31] are used for solving 2D fractional Fitz Hugh-Nagumo monodomain model, which consists of a coupled 2D space fractional nonlinear reaction-diffusion equation and an ordinary differential equation, on irregular domain and rectangle domain respectively. ADI Galerkin-Legendre spectral method [32] is developed for 2D Riesz space fractional nonlinear reaction-diffusion equation.

Most of the above mentioned works contribute on linear fractional differential equations and finite difference method combined with ADI technique. A few work consider ADI FEM [14] [31] or nonlinear fractional differential equations [30] [31] [32] . Compared with FD method, FE method has the advantage of easily handling variable coefficients problem and boundary conditions. And many realistic problems involve nonlinear fractional differential equations. Based on these motivations, our attention in this paper will focus on developing ADI FE schemes for efficiently solving a class of nonlinear time fractional differential equations. This is the first time ADI FE scheme proposed and analyzed rigorously for nonlinear fractional differential equations. We will use problem (1.1) as a model problem to illustrate our approach.

The outline of this paper is organized as follows. In Section 2, we introduce some preliminaries and notations which will be used later. The formulation of ADI finite element method for nonlinear time fractional reaction-subdiffusion equation is presented in Section 3. The stability and error estimates of the proposed method are discussed in Section 4. In convenience of computation, we give the matrix form of ADI finite element scheme in Section 5. Some numerical experiments are displayed in Section 6. It aims to confirm our theoretical results. In the end, some concluding remarks are given in Section 5.

In the following, and denote generic positive constants independent of, and, and their value will not be the same in different equations or inequalities.

2. Preliminary and Notations

Let be a bounded and open domain in. Denote the inner product and norm on by

Recall that the Sobolev space is the closure of in the norm

Denote by the closure of in the norm; it is well known that an equivalent norm on is

If is a normed space with norm, recall that

and

Denote. Let be the finite dimensional subspace of and satisfy

and

In convenience, the following notations will be used. For a positvie integer, let, where is the time step. Denote the grid function

Define linear operator by

(7)

and its variational form

and corresponding energy norm by

Obviously, we have

Some useful lemmas are given as follows.

Lemma 1. [3] Let

then satisfy the following properties

1),

2).

Lemma 2. [3] If, then

where, is bounded by

We state here for convenience the discrete version of Gronwall’s inequality.

Lemma 3. [33] Suppose that and are nonnegative functions defined for, and that is nondecreasing. If

where is a positive constant, then

3. Formulation of ADI FEM

Integrating both sides of (1) with respect to the time variable from to, and noticing the definition (3) and (7), we can obtain

(8)

Applying Lemma 2 and the following integration formula

Equation (8) is equivalent to

(9)

where the remainder term can be bounded by

(10)

The weak form of Equation (9) is: find such that for any,

(11)

Then the finite element approximation to Equation (11) is: find such that for any,

or equivalently

(12)

The choice of the initial values will be discussed later.

Let, then, (12) can be transformed into

(13)

so that the alternating-direction Galerkin scheme of (1) can be defined as, for ,

(14)

where

(15)

Remark 1. Numerical experiments in Section 6 demonstrate that the ADI Galerkin finite element scheme (14) has bad numerical performance for. Similar phenomena have been reported in [11] [16] and [17] , where compact ADI finite difference schemes are designed respectively for solving 2D linear time fractional sub-diffu- sion equations. To construct ADI finite element method, the third term

in left hand side of (14) is extra added. Its effect on temporal accuracy cannot be ignored when. To balance it, we can add a correction term

(16)

on the right hand side of (14). By the way, the similar remedy was also adopted by [11] [16] in finite difference framework.

In conclusion, when, it is beneficial to use the following scheme for

(17)

where

is defined by (15). And for the approximation is still given by (14).

In the following, we will focus our attention on the ADI Galerkin finite element scheme (14).

4. Stability and Error Estimate

Firstly, we introduce some notation and lemmas. Given a smooth function, define by

(18)

or equivalently

The operator defined in (18) has the following approximate properties:

Lemma 4. [34] Let for, , there exists a constant, independent of meshsize, such that

(19)

Lemma 5. [33] If denote the operators and, then

(20)

where.

Lemma 6. Let and are defined in (7) and Lemma 1, respectively. For any positive integer and, let

(21)

then it holds that

Proof. When, it is easily get. Now we consider. Note that

and, we get

By direct algebraic calculation, and noticing the properties of in Lemma 1, we obtain

The proof is completed.

Next, we consider the stability of the ADI Galerkin method (14). Define the following problem dependent norm for any,

(22)

which will be used in stability analysis.

Assume the initial value has an error, which will cause the solution of ADI Galerkin scheme (14), , has a perturbation. Then the stability property of ADI Galerkin methods can be represented as following:

Theorem 1. The ADI Galerkin method (14) is stable with respect to initial value in the problem dependent norm (22), i.e., there exist a positive constant which independent of such that

holds for any.

Proof. The equivalent form of (14) is:

(23)

Then the perturbation equation of (23) can be written as

(24)

where and.

Taking in (24), employing Schwartz inequality and the notation, yields

(25)

Further, by Lipschitz property of and Schwartz inequality, we can estimate the right hand side of (25) as

(26)

Summing for in (25) and using (26) and Lemma 6, we can write

(27)

For sufficiently small, it follows from (27) that

Using discrete Gronwall inequality, we have

Let, we conclude. The proof is completed.

Theorem 2. Let and denote the solutions of (1) and (14) respectively.

Assume that, where. Then, for sufficiently small,

provided the initial value satisfy

Proof. Denote, then. With as in (18) we have from (11) that

(28)

Subtracting (28) from (23) leads to

(29)

Taking, by Schwartz inequality and using the notation, then (29) reduces to

(30)

Now, by Young inequality and Schwartz inequality, we can write

Substitute the above three inequalities into the right hand side of (30), and sum for. Employing Lemma 6, we can write

By discrete Gronwall inequality, if sufficiently small, we can estimate

Consequently, we obtain

(31)

Using the triangle inequality and (31), we get

(32)

It remains to estimate terms on the right-hand side of (32). Firstly, by Lemma 3, we can conclude

(33)

(34)

By (10) and, we easily get

(35)

Secondly, using calculus equality

and Hölder inequality, we have

Further, combined with Lemma 3, we can write

(36)

Since

similar as (36), we can prove

Additionally, according to Lemma 3 and Lemma 4, we have

As a result, we obtain

(37)

Similar as (37), we can write

(38)

Combining (33)-(38), and recalling gives

provided is chosen so that and are. This completes the proof.

Remark 2. Although in our theoretic analysis, we only obtain accuracy in temporal error, numerical experiments in Section 6 demonstrate that temporal error is if. Checking the above analysis process, we will find the error estimates in (37) and (38) are obstacles to obtain temporal error theoretically. This suggests we may take alternative analysis techniques to improve the error estimates in (37) and (38).

Note that we may choose the initial approximation as, where from (18),

This involves an elliptic problem to be solved. With this choice,

In practical computations, it is often sufficient to take as interpolants of in.

5. Matrix Form of ADI FEM

Equations (14) define the ADI finite element method in inner product form. To describe the algebraic problem to which these equations lead, suppose,

where and are finite-dimensional subspaces of, and let

be a tensor product basis for, where and are bases for the subspaces and, respectively. Let

so that

For convenience, we denote

If in (14) we choose, and then

(39)

We define the matrices

and let

with defined similarly. Then the matrix form of (39) is

(40)

where, from (14), the components of are given by

and denotes the tensor product. We may factor (40) in the form

which is equivalent to

where and denote the identity matrices of order and, respectively. Thus we determine by solving two sets of independent one-dimensional problems, first

in the -direction, where, followed by

in the -direction, where. Clearly the computation of each of the vectors and is highly parallel.

6. Numerical Experiments

In this section, two numerical examples are given to demonstrate the effectiveness and accuracy of the ADI Galerkin finite element methods. In all numerical examples, we take the linear tensor product basis

where. is constructed in a similar way. In all examples, we will take the same spatial step size in each direction, i.e..

In our numerical simulation, we present the errors in norm

and numerical convergence orders are computed by

Example 1. Consider the following problem

where

with initial and boundary conditions

where. The exact solution of this equation is

Table 1 shows the L2 norm errors and the temporal convergence orders for = 0.6, 0.7, 0.8, 0.9 with fixed using ADI Galerkin finite element scheme (14). Computational results in Table 1 illustrate that our ADI Galerkin finite element scheme has first order accuracy in time, which is better than our predicted order in Theorem 2.

To investigate the necessary of the correction term (16) in ADI scheme (17) if

, we have compared the two ADI Galerkin finite element scheme (14) and (17)

for = 0.1, 0.2, 0.3, 0.4, with fixed. For saving space, we only present the comparison results of in Table 2, the others cases are similar. The first three columns of Table 2 show the L2 norm errors and its corresponding temporal convergence orders using ADI scheme (14). Computational results demonstrate the temporal

Table 1. L2 errors and temporal convergence orders, fixing h = π/64.

Table 2. Comparison between ADI scheme (14) and (17) for α = 0.1, h = π/64.

convergence order is 0.1, which also suggest our theoretical order proved in Theorem 2 is optimal. The last three columns of Table 2 display the L2 norm errors and its corresponding temporal convergence orders using ADI scheme (17). As we can see, the experiment convergence order is approximately one now. It indicates that the correction term (16) in ADI scheme (17) is beneficial to keep the temporal accuracy. In a word, Table 2 shows ADI scheme (17) has better numerical performance than ADI

scheme (14) if.

Table 3 shows the L2 norm errors and the spatial convergence orders for = 0.6, 0.7, 0.8, 0.9 with fixed using ADI Galerkin finite element scheme (14). The numerical results in Table 3 suggest our ADI Galerkin finite element scheme gets second order accuracy in space, which is consistent with our theoretical result in Theorem 2.

Example 2. Consider the following problem

where

with initial and boundary conditions

where,. The exact solution of this equation is

The nonlinearity of Example 2 is stronger than Example 1. In the following simulation, we have to take much smaller temporal step than Example 1 to obtain good numerical performance. Table 4 shows the L2 norm errors and the temporal convergence orders for = 0.6, 0.7, 0.8, 0.9 with fixed using ADI Galerkin finite element scheme (14). Computational results in Table 4 illustrate that our ADI Galerkin finite element scheme is first order temporal accuracy again, if.

Table 5 displays the comparison between the two ADI Galerkin finite element scheme (14) and (17) for, with fixed. From Table 5, we can conclude that: 1) The first three columns show the order of temporal accuracy of ADI scheme (14) is 0.2 for, confirming our theoretical result in Theorem 2 again; 2) The last three columns illustrate the ADI scheme (17) has first order temporal accuracy, indicating the essentiality of the correction term (16) to keep temporal accuracy once again; 3) To obtain the same level of temporal truncation error, ADI scheme (17) can take much smaller time step than ADI scheme (14) due to its higher accuracy. It also suggests that high order of temporal accuracy is important to time-dependent nonlinear problem.

Table 3. L2 errors and spatial convergence orders, fixing τ = 1/5000.

Table 4. L2 errors and temporal convergence orders, fixing h = π/64.

Table 5. Comparison between ADI scheme (14) and (17) for α = 0.2, h = π/128.

Table 6. L2 errors and spatial convergence orders, fixing τ = 1/5000.

Table 6 shows the L2 norm errors and the spatial convergence orders for = 0.6, 0.7, 0.8, 0.9 with fixed using ADI Galerkin finite element scheme (14). It can be shown from Table 6 that the numerical results are in accordance with the theoretical analysis in Theorem 2.

7. Conclusion

In this work, we proposed an alternating direction Galerkin finite element method for 2D nonlinear time fractional reaction sub-diffusion equation in the Riemann-Liouville type. The stability and convergence of the method are proved for. Numerical results show that our error estimate is optimal. Like the other ADI schemes [16] [17] , the temporal accuracy of our ADI Galerkin finite element method becomes very low if. A remedy is introduced by adding a correction term (15) to keep temporal accuracy.

Acknowledgements

We thank the Editor and the referee for their comments. Research of P. Zhu is funded by the Natural Science Foundation of Zhejiang province, China (Grant No. LY15A010018). This support is greatly appreciated.

Cite this paper

Zhu, P. and Xie, S.L. (2016) ADI Finite Element Method for 2D Nonlinear Time Fractional Reaction- Subdiffusion Equation. American Journal of Computational Mathematics, 6, 336-356. http://dx.doi.org/10.4236/ajcm.2016.64034

References

  1. 1. Liu, Y., Song, S.J. and Xu, S.X. (2003) Advances in the Study on the Chemical Constituents and Biological Activities of Prunella vulgaris L. Shenyang Yike Daxue Xuebao, 20, 55-59.

  2. 2. Qin, J.H. (2008) Preparation of Prunella Vulgaris Extract Composition Used in Medicine. CN Patent No. 101274012 A.

  3. 3. Psotova, J., Svobodova, A., Kolarova, H. and Walterova, D. (2006) Photoprotective Properties of Prunella vulgaris and Rosmarinic Acid on Human Keratinocytes. Journal of Photochemistry and Photobiology B: Biology, 84, 167-174.
    http://dx.doi.org/10.1016/j.jphotobiol.2006.02.012

  4. 4. Cheng, H.Y. and Zhang, Q.F. (2008) Enhanced Analysis of Triterpenes, Flavonoids and Phenolic Compounds in Prunella vulgaris L. by Capillary Zone Electrophoresis with the Addition of Running Buffer Modifiers. Journal of Chromatography A, 1213, 231-238.
    http://dx.doi.org/10.1016/j.chroma.2008.10.033

  5. 5. Sun, W.G., Liao, H.L., Ye, Z.M. and He, G.X. (2003) Chemical and Pharmacological Studies Overview of Prunella vulgari. Zhongguo Zhongyiyao Xinxi Zazhi, 10, 86-88.

  6. 6. Wang, Z.J., Zhao, Y.Y., Chen, Y.Y., et al. (2000) Triterpenoid Compounds of Prunella Genus and Their Features of 13C NMR Spectroscopy. Chinese Materia Medica, 25, 583-588.

  7. 7. Cai, Z.Q., Ma, H.Y. and Zhang, M. (2009) Content Analysis of Oleanolic Acid and Ursolic Acid in Prunella vulgaris Based on Its Provenances and Appearances. Guangdong Yaoxueyuan Xuebao, 25, 256-258.

  8. 8. Sun, Y.M., Xu, J.Z., Wang, Z.A. and Yu, X.P. (2009) Determination of Ursolic Acid in Prunella vulgaris from Different Areas by HPLC. Shizhen Guoyi Guoyao, 20, 1125-1126.

  9. 9. Kojima, H. and Ogura, H. (1986) Triterpenoids from Prunella vulgaris. Phytochemistry, 25, 729-729.
    http://dx.doi.org/10.1016/0031-9422(86)88033-5

  10. 10. Kojima, H., Tominaga, H., Sato, S., Ogura, H., et al. (1987) Pentacyclic Triterpenoids from Prunella vulgaris. Phytochemistry, 26, 1107-1111.
    http://dx.doi.org/10.1016/S0031-9422(00)82359-6

  11. 11. Kojima, H., Tominaga, H. and Sato, S. (1988) Two Novel Hexacyclic Triterpenoids from Prunella vulgaris. Phytochemistry, 27, 2921-2925.
    http://dx.doi.org/10.1016/0031-9422(88)80689-7

  12. 12. Ryu, S.Y., Oak, M.H., Yoon, S.-K., Cho, D.-I., Yoo, G.-S., Kim, T.-S. and Kim, K.-M. (2000) Anti-Allergic and Anti-Inflammatory Triterpenes from the Herb of Prunella vulgaris. Planta Medica, 66, 358-360.
    http://dx.doi.org/10.1055/s-2000-8531

  13. 13. Gai, C.Y., Kong, D.Y., Wang, S.G., et al. (2010) Study on Chemical Constituents of Prunella vulgaris L. Chinese Journal of Pharm, 41, 8580-8582.

  14. 14. Zhang, L.Z., Guo, Y.J., Tu, G.Z., et al. (2008) A Novel Triterpenoid Saponin from Prunella vulgaris. Yaoxue Xuebao, 43, 169-172.

  15. 15. Lee, I.K., Kim, D.H., Lee, S.Y., Kim, K.R., Choi, S.U., Hong, J.K., Lee, J.H., Hyun, L.J. and Hyun, P.Y. and Ro, L.K. (2008) Triterpenoic Acids of Prunella vulgaris var. lilacina and Their Cytotoxic Activities in Vitro. Archives of Pharmacal Research, 31, 1578-1583.
    http://dx.doi.org/10.1007/s12272-001-2154-6

  16. 16. Zhang, J.Y. and Yang, C.R. (1995) The Two New Ursane Glycosides from Prunella vulgaris in France. Yunnan Zhiwu Yanjiu, 17, 468-472.

  17. 17. Wang, Z.J., Zhao, Y.Y., Tu, G.Z., Hong, S.L. and Chen, Y.Y. (1999) Studies on Chemical Constituents from Prunella vulgaris. Huaxue Xuebao, 34, 679-681.

  18. 18. Hisashi, K., Noriko, S., Akiko, H. and Haruo, O. (1990) Constituents of the Labiatae Plants Part 5. Sterol Glucosides from Prunella vulgaris. Phytochemistry, 29, 2351-2355.
    http://dx.doi.org/10.1016/0031-9422(90)83073-A

  19. 19. Meng, Z.M. and He, L.W. (1995) Studies on Constituent of Prunella vulgaris L. Zhongguo Yaoke Daxue Xuebao, 26, 329-331.

  20. 20. Liu, B., Ma, G.P. and Shi, R.B. (2002) The Determination of Cyasterone in Prunella vulgaris L Var. Leucantha Schur Sec. Bailey Using RP-HPLC. Chinese Traditional and Herbal Drugs, 33, 898-899.

  21. 21. Tian, J., Xiao, Y.Y., Zhao, Y.Y., et al. (2000) Structure Identification of New Compound Vulgarsaponin a from Prunella vulgaris. Yaoxue Xuebao, 35, 29-31.

  22. 22. Psotova, J., Chlopcikova, S., Miketova, P. and Simánek, V. (2005) Cytoprotectivity of Prunella vulgaris on Doxorubicin-Treated Rat Cardiomyocytes. Fitoterapia, 76, 556-561.
    http://dx.doi.org/10.1016/j.fitote.2005.04.019

  23. 23. Zhu, J.U., Wang, Z.J., Zhao, Y.Y., et al. (2001) Depsides from Prunella vulgaris. Zhongguo Shiyan Fangjixue Zazhi, S1, 157-161.

  24. 24. Hu, X., Cui, S., Chen, X. and Hu, Z.D. (2009) CE with Field-Enhanced Stacking for Rapid and Sensitive Determination of Umbelliferone, Rutin and Aesculetin in Prunella vulgaris. Chromatographia, 70, 1733-1736.
    http://dx.doi.org/10.1365/s10337-009-1373-8

  25. 25. Jozef, S. (1963) Phytochemical Studies on Prunella vulgaris and Prunella Grandiflora Saponin and Triterpene Compounds. Dissertations Pharm, 15, 333-333.

  26. 26. Dmitruk, I.S., Dmitruk, S.E., Berezovskaya, T.P., et al. (1987) Flavonoids of Vulgaris. Khimiya Prirodnykh Soedinenii, 3, 449-449.

  27. 27. Dmitruk, I.S. (1987) Coumarins of Prunella vulgaris. Khimiya Prirodnykh Soedinenii, 4, 510-510.

  28. 28. Yang, L.J., Li, Z.Q., Pu, F., et al. (1988) The Chemical Composition of the Essential Oil of Prunella vulgaris Liun. Yaowu Fenxi Zazhi, 8, 264-265.

  29. 29. Wang, H.B., Zhang, Z.Y. and Su, Z.W. (1994) The Constituents of the Essential Oil from Three Plants of Prunella vulgari. Zhongguo Yaoxue Zazhi, 29, 652-653.

  30. 30. Xu, Z.X., Zhou, Q.Q. and Xu, S.L. (1996) Recent Research Progress on Chemical Constituents and Biological Activities of Prunella vulgaris. Zhongchengyao, 18, 42-42.

  31. 31. Tabba, H.D., Chang, R.S. and Smith, K.M. (1989) Isolation, Purification and Partial Characterization of Prunellin, an Anti-HIV Component from Aqueous Extracts of Prunella vulgaris. Antiviral Research, 11, 263-273.
    http://dx.doi.org/10.1016/0166-3542(89)90036-3

  32. 32. Natherova, L., Leifertora, I. and Kunetkova, M. (1973) Evaluation of Flavonoids in the Domestic Specices of Genus Fragaria L. Ceskoslovenská Farmacie, 22, 441-443.

  33. 33. Feng, Y., Xue, M., Jiang, L.H., et al. (2008) Chemical Study on Water Soluble Polysaccharides from Prunella vulgaris L. Zhongguo Yiyuan Yaoxue Zazhi, 28, 431-434.

  34. 34. Rasool, R., Ganai, B.A., Akbar, S., Kamili, A.N. and Masood, A. (2010) Phytochemical Screening of Prunella vulgaris L.—An Important Medicinal Plant of Kashmir. Pakistan Journal of Pharmaceutical Sciences, 23, 399-402.

  35. 35. Wang, Q.X. (1998) Treatment of Hypertension by the Effective Remedy. Shizhen Guoyi Guoyao, 9, 342-343.

  36. 36. Jia, C.C., Wang, X.J. and Luan, Y.Y. (1999) External Usage of Traditional Chinese Medicine in the Treatment of Hypertension. Zhongguo Minjian Liaofa, 7, 14-15.

  37. 37. He, Y.Q., Li, R.Z., Feng, L.Z. and Li, Z.P. (1985) Studies on the Chemical Constituents of Prunella vulgaris (I). Beijing Yika Daxue Xuebao, 17, 297-299.

  38. 38. Li, Y.H., Niu, X. and Li, Y.G. (1996) Research on the Antihypertensive Activity of Sancaojiangyatang. Beijing Zhongyiyao Daxue Xuebao, 19, 45-46.

  39. 39. Wang, H.B., Zhang, Z.Y., Su, Z.W., et al. (1994) On the Effect of Total Saponins from Common Selfheal (Prunell vulgaris) on Experimental Myocardial Infarction and Hypertension of Anesthetized Rats. Chinese Traditional and Herbal Drugs, 25, 302-303.

  40. 40. Feng, P.F., Qin, N.P., Fang, R.Y., et al. (1998) Effect of Sanwu Hypertensive Decoction on Blood Pressure and Lymphokine-Activated Killer Cell in SHR. Zhongguo Xunhuan Zazhi, 13, 178-180.

  41. 41. Panza, J.A., Carcia, C.E., Kileoyne, C.M., Quyyumi, A.A. and Cannon III, R.O. (1995) Impaired Endochelium Dependent Vasodilation in Patients with EH Evidence that Nitric Oxide Abnormality Is Not Localized to a Angle Aignal Transduction Pathway. Circulation, 91, 1732-1738.
    http://dx.doi.org/10.1161/01.CIR.91.6.1732

  42. 42. Kurmar, K.V. and Das, U.N. (1993) Are Free Radical Involved in the Pathobiology of Human Essential Hypertension. Free Radical Research, 19, 59-66.
    http://dx.doi.org/10.3109/10715769309056499

  43. 43. Chen, W.H. and He, J.Y. (1997) Antagonistic Effects of Ephedra Sinica, Prunlla vulgaris and Cuttlefish Bone on the Model of Rat Acute Blood Stasis. Beijing Zhongyiyao Daxue Xuebao, 20, 39-41.

  44. 44. Liu, J.X., Qin, Y.J. and Zhang, J.Y. (1998) Experimental Study on Treatment of Endometriorsis in Rabbit Model with the Method of Removing Blood Stasis and Resolving Phlegm, Softening and Resolving the Lump. Shangdong Zhongyiyao Daxue Xuebao, 22, 227-229.

  45. 45. Li, S.C., Fan, J.F., Li, S.P., et al. (2001) Observation on Curative Effects of Supplemented Rhizoma Polygonati Sicao Decoction on the Patients with Ischemic Brain Damage. Zhongguo Zhongxiyi Jijiu Zazhi, 8, 376-377.

  46. 46. Liang, X.L. (1998) Study on the Effect of the Model with Antilipidemic Activity with Sian Capsule. Chengdu Zhongyiiyao Daxue Xuebao, 21, 39-41.

  47. 47. Psotova, J., Kolar, M., Sousek, J., Svagera, Z., Vicar, J. and Ulrichová, J. (2003) Biological Activities of Prunella vulgaris Extract. Phytotherapy Research, 17, 1082-1087.
    http://dx.doi.org/10.1002/ptr.1324

  48. 48. Wang, Z.J., Zhao, Y.Y., Chen, Y.Y., et al. (2001) Chemical Constituents and Pharmacological Activities of Prunella Genus. World Phytomedicines, 16, 7-9.

  49. 49. Zheng, M. (1990) Experimental Study of 472 Herbs with Antiviral Action against the Herpes Simplex Virus. Zhongxiyi Jiehe Zazhi, 10, 39-41.

  50. 50. Zheng, M.S. and Li, W. (1991) Experimental Investigation into Antiviral Action of Prunella vulgaris L. on Type I Herpes Simplex Virus. Jiangxi Yixueyuan Xuebao, 31, 15-17.

  51. 51. Chen, Q., Ceng, Y.G. and Cao, M.C. (2002) Research on the Analgesic and Anti-Inflammatory Activity of the Oral Drench Made from Prunella Vulgaries L. Jiceng Zhongyao Zazhi, 16, 6-7.

  52. 52. Tang, C.K., Chen, G.J., Shen, Y.Q., et al. (1999) The Antipyretic and Anti-Inflammatory Activity of the Pills Made from Prunella vulgarites L. Zhongguo Shiyan Fangjixue Zazhi, 5, 54-55.

  53. 53. Xiao, L.Y. and Huang, C.P. (2001) A Discussion on Sensitivity of 23 Chinese Herbage Medicines against MRSA. Shizhen Guoyi Guoyao, 12, 878-879.

  54. 54. Zhang, F.X., Deng, W.D., Hu, Y.J. and Wu, X.X. (1999) Inhibitory Effect of Aikeqing on the Activity of Immunodeficiency Virus of Simian in Vitro. Guangzhou Zhongyiyao Daxue Xuebao, 16, 127-129.

  55. 55. Fang, X.Y., Chang, R.C.C., Yuen, W.H. and Zee, S.Y. (2005) Immune Modulatory Effects of Prunella vulgaris L. International Journal of Molecular Medicine, 15, 491-496.

  56. 56. Xu, H.X., Lee, S.H.S., Lee, S.F., White, R.L. and Blay, J. (1999) Isolation and Characterization of an Anti-HSV Polysaccharide from Prunella vulgaris. Antiviral Research, 44, 43-54.
    http://dx.doi.org/10.1016/S0166-3542(99)00053-4

  57. 57. Lam, T.L., Lam, M.L., Au, T.K., Ip, D.T.M., Ng, T.B., Fong, W.P. and Wan, D.C.C. (2000) A Comparison of Human Immunodeficiency Virus Type-1 Protease Inhibition Activities by the Aqueous and Methanol Extracts of Chinese Medicinal Herbs. Life Sciences, 67, 2889-2896.
    http://dx.doi.org/10.1016/S0024-3205(00)00864-X

  58. 58. Kageyama, S., Kurokawa, M. and Shiraki, K. (2000) Extract of Prunella vulgaris Spikes Inhibits HIV Replication at Reverse Transcription in Vitro and Can Be Absorbed from Intestine in Vivo. Antiviral Chemistry & Chemotherapy, 11, 157-164.

  59. 59. Yamasaki, K., Nakano, M., Kawahata, T., Mori, H., Otake, T., Ueba, N., Oishi, I., Inami, R., Yamne, M., Nkamura, M., Murata, H. and Naknishi, T. (1998) Anti-HIV-1 Activity of Herbs in Labiatae. Biological & Pharmaceutical Bulletin, 21, 829-833.
    http://dx.doi.org/10.1248/bpb.21.829

  60. 60. Yamasaki, K., Otake, T., Mori, H., Morimoto, M., Ueba, N., Kurokawa, Y., Shiota, K. and Yuge, T. (1993) Screening Test of Crude Drug Extract on Anti-HIV Activity. Yakugaku Zasshi: Journal of the Pharmaceutical Society of Japan, 113, 818-824.

  61. 61. Au, T., Lam, T., Ng, T., Fong, W. and Wan, D. (2001) A Comparison of HIV-1 Integrase Inhibition by Aqueous and Methanol Extracts of Chinese Medicinal Herbs. Life Sciences, 68, 1687-1694.
    http://dx.doi.org/10.1016/S0024-3205(01)00945-6

  62. 62. Zheng, M.S. and Zhang, Y.Z. (1990) Anti-HBsAg Herbs Employing ELISA Technique. Zhongxiyi Jihe Zazhi, 10, 560-562.

  63. 63. Zheng, J., He, J.G., Ji, B.P., Li, Y. and Zhang, X.F. (2007) Antihyperglycemic Activity of Prunella vulgaris L. in Streptozotocin-I Nduced Diabetic Mice. Asia Pacific Journal of Clinical Nutrition, 16, 427-431.

  64. 64. Huang, N., Hauck, C., Yum, M.Y., Rizshsky, L., Widrlechner, M.P., Mccoy, J.A., Murphy, P.A., Dixon, P.M., Nikolau, B.J. and Birt, D.F. (2009) Rosmarinic Acid in Prunella vulgaris Ethanol Extract Inhibits Lipopolysaccharide-Induced Prostaglandin E2 and Nitric Oxide in RAW 264.7 Mouse Macrophages. Journal of Agricultural and Food Chemistry, 57, 10579-10589.
    http://dx.doi.org/10.1021/jf9023728

  65. 65. Zdarilová, A., Svobodová, A., Simánek, V. and Ulrichová, J. (2009) Prunella vulgaris Extract and Rosmarinic Acid Suppress Lipopolysaccharide-Induced Alteration in Human Gingival Fibroblasts. Toxicology in Vitro, 23, 386-392.
    http://dx.doi.org/10.1016/j.tiv.2008.12.021

  66. 66. Jung, Y.B., Roh, K.J., Jung, J.A., Jung, K., Yoo, H., Cho, Y.B., Kwak, W.J., Kim, D.K., Kim, K.H. and Han, C.K. (2001) Effect of SKI 306X, a New Herbal Anti-Arthritic Agent, in Patients with Osteoarthritis of the Knee: A Double-Blind Placebo Controlled Study. The American Journal of Chinese Medicine, 29, 485-491.
    http://dx.doi.org/10.1142/S0192415X01000502

  67. 67. Choi, J.H., Kim, D.Y., Yoon, J.H., Youn, H.Y., Yi, J., Rhee, H.I., Ryu, K., Jung, K. and Han, C.K. (2002) Effects of SKI 306X, a New Herbal Agent, on Proteoglycan Degradation in Cartilage Explant Culture and Collagenase-Induced Rabbit Osteoarthritis Model. Osteoarthritis and Cartilage, 10, 471-478.
    http://dx.doi.org/10.1053/joca.2002.0526

  68. 68. Jiang, Y., Jun, J.H. and Sun, X.Y. (1988) The Effect of Prunella vulgaris L on the Thymus, Spleen and Adrenalin of Animal. Gansu Yiyao, 7, 4-7.

  69. 69. Fang, X., Yu, M.M.S., Yuen, W.H., Zee, S.Y. and Chang, R.C. (2005) Immune Modulatory Effects of Prunella vulgaris L. on Monocytes/Macrophages. International Journal of Molecular Medicine, 16, 1109-1116.

  70. 70. Ma, D.E., Wang, Z.M. and Ma, A.Y. (1983) The Anti-Inflammatory Activity and the Effect on the Immune Organs of Prunella vulgaris. Shanxi Yiyao Zazhi, 12, 4-7.

  71. 71. Xu, L.S. (1989) Pharmacological Research on the Hypoglycemic Effect of the Active Ingredienst in Prunella vulgaris. Chinese Traditional and Herbal Drugs, 20, 22-24.

  72. 72. Liu, B.L., Zhu, D.N. and Wang, G. (1995) Effects of the Alcohol Extract of Spica Pranellae on Bloodglucose in Mice. Zhongguo Yaoke Daxue Xuebao, 26, 44-46.

  73. 73. Feng, M.L., Jia, L.L., Wu, Y.P., et al. (2000) Effect of the Alcoholic Extraction of Spica Prunellae on Experimental Diabetic Nephropathy. Shanxi Zhongyi Xueyuan Xuebao, 1, 7-9.

  74. 74. Wang, J.G. (2001) Liver-Protective Effect of Prunella vulgaris Mixture. Chinese Traditional and Herb Drugs, 32, 625-627.

  75. 75. Zhang, J. and Tao, X.P. (2000) the Effect of Prunella vulgaris on Liver Fibrosis Indexes. Jiceng Zhongyao Zazhi, 14, 60-60.

  76. 76. Meng, G., Zhang, K.J. and Zhang, M.Z. (2007) Chemical Constituents of Prunella vulgaris L and Antitumor Activity. Northwest Pharmaceutical Journal, 22, 211-213.

  77. 77. Liu, L., Xu, D.S., Zhou, R.Y. and Zhong, Y. (2008) Effective Fraction of Prunella Vulgaris and Its Application in Preparation of Medicines for Treating Colon Cancer. CN Patent No. 101317883 A.

  78. 78. Wang, K., Dong, H.F., Zhang, X.Y., et al. (2000) The Effect of Prunella vulgaris L on SGC-7901 Cells. Shanghai Yixue Jianyan Zazhi, 15, 305-306.

  79. 79. Lee, K.H., Lin, Y.M., Wu, T.S., Zhang, D.C., Yamagishi, T., Hayashi, T., Hall, I.H., Chang, J.J., Wu, R.Y. and Yang, T.H. (1988) The Cytotoxic Principles of Prunella vulgaris, Psychotria serpens, and Hyptis capitata: Ursolic Acid and Related Derivatives. Planta Medica, 54, 308-311.
    http://dx.doi.org/10.1055/s-2006-962441

  80. 80. Xu, Z.W., Zhou, R.Y., Wang, W.H., et al. (2001) Mechanism Study of “Prunella Injection” on Formation of Pleural Fibrosis. Zhejiang Zhongxiyi Jiehe Zazhi, 11, 5-8.

  81. 81. Zhou, R.Y., Xu, Z.W. and Ni, A.D. (2001) Clinical and Experimental Observations of Hydrothorax in Lung Cancer Cases Treated with Closed Drainage and Injection of Selfheal Spike Injection. Shanghai Daxue Xuebao, 15, 49-51.

  82. 82. Chen, C.Y., Wu, G. and Zhang, M.Z. (2009) The Effects and Mechanism of Action of Prunella vulgaris L Extract on Jurkat Human T Lymphoma Cell Proliferation. Chinese-German Journal of Clinical Oncology, 8, 426-429.

  83. 83. Zhang, M.Z. and Liu, H.M. (2009) Method for Extracting Anti-Tumor Effective Parts from Chinese Medicine Prunella. CN Patent No. 101461842 A.

  84. 84. Lee, H. and Lin, J.Y. (1988) Antimutagenic Activity of Extracts from Anticancer Drugs in Chinese Medicine. Mutation Research/Genetic Toxicology, 204, 229-234.

  85. 85. Lamaison, J., Petitjean-Freytet, C. and Carnat, A. (1990) Medicinal Lamiaceae with Antioxidant Properties, a Potential Source of Rosmarinic Acid. Pharmaceutica Acta Helvetiae, 66, 185-188.

  86. 86. Liu, J. (2005) Oleanolic Acid and Ursolic Acid: Research Perspectives. Journal of Ethnopharmacology, 100, 92-94.
    http://dx.doi.org/10.1016/j.jep.2005.05.024

  87. 87. Wang, H.B., Zhang, Z.Y., Zai, Z.X., Su, Z. and Li, C.K. (1993) Qualitative Analysis of Chinese Drug Xiakucao (Prunella). Zhongguo Zhongyao Zazhi, 18, 655-657.

  88. 88. Muto, Y., Ninomiya, M. and Fujiki, H. (1990) Present Status of Research on Cancer Chemoprevention in Japan. Japanese Journal of Clinical Oncology, 20, 219-224.

  89. 89. Niikawa, M., Hayashi, H., Sato, T., Nagase, H. and Kito, H. (1993) Isolation of Substances from Glossy Privet (Ligustrum lucidum Ait.) Inhibiting the Mutagenicity of Benzo[A]Pyrene in Bacteria. Mutation Research/Genetic Toxicology, 319, 1-9.

  90. 90. Young, H., Chung, H., Lee, C., Park, K., Yokozawa, T. and Oura, H. (1994) Ursolic Acid Inhibits Aflatoxin B1-Induced Mutagenicity in a Salmonella Assay System. Biological & Pharmaceutical Bulletin, 17, 990-992.
    http://dx.doi.org/10.1248/bpb.17.990

  91. 91. Huang, M.T., Ho, C.T., Wang, Z.Y., Ferraro, T., Lou, Y.R., Stauber, K., Ma, W., Georgiadis, C., Laskin, J.D. and Conney, A.H. (1994) Inhibition of Skin Tumorigenesis by Rosemary and Its Constituents Carnosol and Ursolic Acid. Cancer Research, 54, 701-708.

  92. 92. Wang, J.J., Wang, B., Guo, J., Gao, Y., Xu, Q. and Chen, W.S. (2000) Inhibitory Effect of Ursolic Acid on Angiogenesis in Vitro. Academic Journal of Second Military Medical University, 21, 1071-1073.

  93. 93. Balanehru, S. and Nagarajan, B. (1991) Protective Effect of Oleanolic Acid and Ursolic Acid against Lipid Peroxidation. Biochemistry International, 24, 981-990.

  94. 94. Ringbom, T., Segura, L., Noreen, Y., Perera, P. and Bohlin, L. (1998) Ursolic Acid from Plantago Major, a Selective Inhibitor of Cyclooxygenase-2 Catalyzed Prostaglandin Biosynthesis. Journal of Natural Products, 61, 1212-1215.
    http://dx.doi.org/10.1021/np980088i

  95. 95. Subbaramaiah, K., Michaluart, P., Sporn, M.B. and Dannenberg, A.J. (2000) Ursolic Acid Inhibits Cyclooxygenase-2 Transcription in Human Mammary Epithelial Cells. Cancer Research, 60, 2399-2404.

  96. 96. Zhao, G.Q. (1996) Antineoplastic Activity of Ursolic Acid in Loquat Leaves Guowai Yiyao. Zhiwuxue Fence, 11, 180-180.

  97. 97. Lee, H.Y., Chung, H.Y., Kim, K.H., Lee, J.J. and Kim, K.W. (1994) Induction of Differentiation in the Cultured F9 Teratocarcinoma Stem Cells by Triterpene Acids. Journal of Cancer Research and Clinical Oncology, 120, 513-518.
    http://dx.doi.org/10.1007/BF01221027

  98. 98. Paik, K.J., Jeon, S.S., Chung, H.Y., Lee, K.H., Kim, K.W., Chung, J.K. and Kim, N.D. (1998) Induction of Differentiation of the Cultured Rat Mammary Epithelial Cells by Triterpene Acids. Archives of Pharmacal Research, 21, 398-405.
    http://dx.doi.org/10.1007/BF02974633

  99. 99. Hanahan, D., Christofori, G., Naik, P. and Arbeit, J. (1996) Transgenic Mouse Models of Tumour Angiogenesis: The Angiogenic Switch, Its Molecular Controls, and Prospects for Preclinical Therapeutic Models. European Journal of Cancer, 32, 2386-2393.
    http://dx.doi.org/10.1016/S0959-8049(96)00401-7

  100. 100. Sohn, K.H., Lee, H.Y., Chung, H.Y., Young, H.S., Yi, S.Y. and Kim, K.W. (1995) Anti-Angiogenic Activity of Triterpene Acids. Cancer Letters, 94, 213-218.
    http://dx.doi.org/10.1016/0304-3835(95)03856-R

  101. 101. Wang, B., Wang, J.J. and Xu, J. (2001) Inhibitory Effect of Ursolic Acid on Angiogenesis in Vitro. Zhongliu Fangzhi Zazhi, 8, 351-352.

  102. 102. Baek, J.H., Lee, Y.S., Kang, C.M., Kim, J., Kwon, K.S., Son, H.C. and Kim, K.W. (1997) Intracellular Ca2+ Release Mediates Ursolic Acid-Induced Apoptosis in Human Leukemic HL-60 Cells. International Journal of Cancer, 73, 725-728.
    http://dx.doi.org/10.1002/(SICI)1097-0215(19971127)73:5<725::AID-IJC19>3.0.CO;2-4

  103. 103. Huang, J., Sun, Y., Lu, S.X., Su, T. and Jiao, S.C. (1999) Experimental Study on Apoptosis Induced by Ursolic Acid Isolated from Asparagus in HL260 Cells. Zhongguo Zhongxiyijiehe Zazhi, 19, 296-298.

  104. 104. Xu, G.F., Zhao, X.L. and Zhao, L. (2000) Apoptosis Inducde by Flavonoids Extract of Wheat Germ in a Human Breast Cancer Cell Line. Yingyang Xuebao, 22, 43-46.

  105. 105. Wang, C., Zhang, L.S. and He, T. (2002) Study on Antiproliferation Effects of Genistein in Vitro. Zhongguo Gonggong Weisheng, 18, 1056-1058.

  106. 106. Trochon, V., Blot, E., Cymbalista, F., Engelmann, C., Tang, R.P., Thoma&iumldis, A., Vasse, M., Soria, J., Lu, H. and Soria, C. (2000) Apigenin Inhibits Endothelial-Cell Proliferation in G2/M Phase Whereas It Stimulates Smooth-Muscle Cells by Inhibiting P21 and P27 Expression. International Journal of Cancer, 85, 691-696.
    http://dx.doi.org/10.1002/(SICI)1097-0215(20000301)85:5<691::AID-IJC15>3.0.CO;2-Q

  107. 107. Zi, X., Zhang, J., Agarwal, R. and Pollak, M. (2000) Silibinin Up-Regulates Insulin-Like Growth Factor-Binding Protein 3 Expression and Inhibits Proliferation of Androgen-Independent Prostate Cancer Cells. Cancer Research, 60, 5617-5620.

  108. 108. Senderowicz, A.M. (1999) Flavopiridol: The First Cyclin-Dependent Kinase Inhibitor in Human Clinical Trials. Investigational New Drugs, 17, 313-320.
    http://dx.doi.org/10.1023/A:1006353008903

  109. 109. Huynh, H.T. and Teel, R.W. (1999) Selective Induction of Apoptosis in Human Mammary Cancer Cells (MCF-7) by Pycnogenol. Anticancer Research, 20, 2417-2420.

  110. 110. Wu, B., Xu, G.F., Zhao, X.L. and Ren, X. (2001) Antioxidation of Flavones of Wheat Germ on Mammary Tulnor of Rats. Weisheng Yanjiu, 30, 215-217.

  111. 111. Chen, J.W., Hu, T.X. and Zhu, D.Y. (2002) Study on Structure-Activity Relationship of Eleven Natural Flavonoids Scavenging Superoxide Anion. Zhongguo Yaoxue Zazhi, 37, 57-58.

  112. 112. Zhang, R.Q. and Han, Z.K. (1994) The Effect of Flavonoids on the Immune Function and the Level of Β-Endorphins in the Blood of Mouse. Zhongguo Mianyi Zazhi, 10, 91-92.

  113. 113. Rafi, M.M., Rosen, R.T., Vassil, A., Ho, C.T., Zhang, H., Ghai, G., Lambert, G. and Dipaola, R.S. (1999) Modulation of Bcl-2 and Cytotoxicity by Licochalcone-A, a Novel Estrogenic Flavonoid. Anticancer Research, 20, 2653-2658.

  114. 114. Mcvean, M., Xiao, H., Isobe, K.I. and Pelling, J.C. (2000) Increase in Wild-Type P53 Stability and Transactivational Activity by the Chemopreventive Agent Apigenin in Keratinocytes. Carcinogenesis, 21, 633-639.
    http://dx.doi.org/10.1093/carcin/21.4.633

  115. 115. Chan, F.L., Choi, H., Chen, Z., Chan, P.S. and Huang, Y. (2000) Induction of Apoptosis in Prostate Cancer Cell Lines by a Flavonoid, Baicalin. Cancer Letters, 160, 219-228.
    http://dx.doi.org/10.1016/S0304-3835(00)00591-7

  116. 116. Wenzel, U., Kuntz, S., Brendel, M.D. and Daniel, H. (2000) Dietary Flavone Is a Potent Apoptosis Inducer in Human Colon Carcinoma Cells. Cancer Research, 60, 3823-3831.

  117. 117. Ogata, S., Miyake, Y., Yamamoto, K., Okumura, K. and Taguchi, H. (2000) Apoptosis Induced by the Flavonoid from Lemon Fruit (Citrus limon BURM. F.) and Its Metabolites in HL-60 Cells. Bioscience, Biotechnology, and Biochemistry, 64, 1075-1078.
    http://dx.doi.org/10.1271/bbb.64.1075

  118. 118. Blankson, H., Grotter&oslashd, E. and Seglen, P. (2000) Prevention of Toxin-Induced Cytoskeletal Disruption and Apoptotic Liver Cell Death by the Grapefruit Flavonoid, Naringin. Cell Death & Differentiation, 7, 739-746.
    http://dx.doi.org/10.1038/sj.cdd.4400705

  119. 119. Jiang, C., Agarwal, R. and Lü, J. (2000) Anti-Angiogenic Potential of a Cancer Chemopreventive Flavonoid Antioxidant, Silymarin: Inhibition of Key Attributes of Vascular Endothelial Cells and Angiogenic Cytokine Secretion by Cancer Epithelial Cells. Biochemical and Biophysical Research Communications, 276, 371-378.
    http://dx.doi.org/10.1006/bbrc.2000.3474

  120. 120. Ishiwa, J., Sato, T., Mimaki, Y., Sashida, Y., Yano, M. and Ito, A. (2000) A Citrus Flavonoid, Nobiletin, Suppresses Production and Gene Expression of Matrix Metalloproteinase 9/Gelatinase B in Rabbit Synovial Fibroblasts. The Journal of Rheumatology, 27, 20-25.

  121. 121. Nakahata, N., Kyo, R., Kutsuwa, M. and Ohizumi, Y. (1999) Inhibition of Mitogen-Activated Protein Kinase Cascade by Baicalein, a Flavonoid of Natural Origin. Nippon Yakurigaku Zasshi, 114, 215-219.
    http://dx.doi.org/10.1254/fpj.114.supplement_215

  122. 122. Zhou, J., Purna, M. and Steven, K. (1998) Soybean Components Inhibit the Growth of Human Prostate Cancer Cell Line Lncap in SCID Mice via Alteration in Cells Apoptosis, Angiogenesis and Proliferation. FASEB Journal, 18, 3822.

  123. 123. Ranelletti, F.O., Maggiano, N., Serra, F.G., Ricci, R., Larocca, L.M., Lanza, P., Scambia, G., Fattorossi, A., Capelli, A. and Piantelli, M. (2000) Quercetin Inhibits P21-RAS Expression in Human Colon Cancer Cell Lines and in Primary Colorectal Tumors. International Journal of Cancer, 85, 438-445.
    http://dx.doi.org/10.1002/(SICI)1097-0215(20000201)85:3<438::AID-IJC22>3.0.CO;2-F

  124. 124. Fotsis, T., Pepper, M., Adlercreutz, H., Hase, T., Montesano, R. and Schweigerer, L. (1995) Genistein, a Dietary Ingested Isoflavonoid, Inhibits Cell Proliferation and in Vitro Angiogenesis. The Journal of Nutrition, 125, 790S-797S.

  125. 125. Shin, T.Y., Kim, Y.K. and Kim, H.M. (2001) Inhibition of Immediate-Type Allergic Reactions by Prunella vulgaris in a Murine Model. Immunopharmacology and Immunotoxicology, 23, 423-435.
    http://dx.doi.org/10.1081/IPH-100107341

  126. 126. Kim, S.Y., Kim, S.H., Shin, H.Y., Lim, J.P., Chae, B.S., Park, J.S., Hong, S.G., Kim, M.S., Jo, D.G., Park, W.H. and Shin, T.Y. (2007) Effects of Prunella vulgaris on Mast Cell-Mediated Allergic Reaction and Inflammatory Cytokine Production. Experimental Biology and Medicine, 232, 921-926.

  127. 127. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.

  128. 128. Li, C. and Ding, H. (2014) Higher Order Finite Difference Method for the Reaction and Anomalous-Diffusion Equation. Applied Mathematical Modelling, 38, 3802-3821.
    https://doi.org/10.1016/j.apm.2013.12.002

  129. 129. Zhuang, P., Liu, F., Anh, V., et al. (2009) Stability and Convergence of an Implicit Numerical Method for the Nonlinear Fractional Reaction-Subdiffusion Process. SIAM Journal on Mathematical Analysis, 74, 645-667.

  130. 130. Dehghan, M., Abbaszadeh, M. and Mohebbi, A. (2015) Error Estimate for the Numerical Solution of Fractional Reaction-Subdiffusion Process Based on a Meshless Method. Journal of Computational and Applied Mathematics, 280, 14-36.
    https://doi.org/10.1016/j.cam.2014.11.020

  131. 131. Yu, B., Jiang, X. and Xu, H. (2015) A Novel Compact Numerical Method for Solving the Two-Dimensional Non-Linear Fractional Reaction-Subdiffusion Equation. Numerical Algorithms, 68, 923-950.
    https://doi.org/10.1007/s11075-014-9877-1

  132. 132. Douglas, J. (1955) On the Numerical Integration of Uxx+Uyy=Ut by Implicit Methods. Journal of the Society for Industrial and Applied Mathematics, 3, 42-65.

  133. 133. Douglas, J. and Gunn, J.E. (1964) A General Formulation of Alternating Direction Method, Part I. Parabolic and Hyperbolic Problem. Numerische Mathematik, 6, 428-453.
    https://doi.org/10.1007/BF01386093

  134. 134. Peaceman, D.W. and Rachford, H.H. (1955) The Numerical Solutions of Parabolic and Elliptic Differential Equations. Journal of the Society for Industrial and Applied Mathematics, 3, 28-41.
    https://doi.org/10.1137/0103003

  135. 135. Meerschaert, M.M., Scheffler, H.P. and Tadjeran, C. (2006) Finite Difference Methods for Two-Dimensional Fractional Dispersion Equation. Journal of Computational Physics, 211, 249-261.
    https://doi.org/10.1016/j.jcp.2005.05.017

  136. 136. Zhang, Y. and Sun, Z. (2011) Alternating Direction Implicit Schemes for the Two-Dimensional Fractional Sub-Diffusion Equation. Journal of Computational Physics, 230, 8713-8728.
    https://doi.org/10.1016/j.jcp.2011.08.020

  137. 137. Cui, M. (2013) Convergence Analysis of High-Order Compact Alternating Direction Implicit Schemes for the Two-Dimensional Time Fractional Diffusion Equation. Numerical Algorithms, 62, 383-409.
    https://doi.org/10.1007/s11075-012-9589-3

  138. 138. Zhang, Y., Sun, Z. and Zhao, X. (2012) Compact Alternating Direction Implicit Scheme for the Two-Dimensional Fractional Diffusion-Wave Equation. SIAM Journal on Numerical Analysis, 50, 1535-1555.
    https://doi.org/10.1137/110840959

  139. 139. Wang, Z. and Vong, S. (2015) A High-Order ADI Scheme for the Two-Dimensional Time Fractional Diffusion-Wave Equation. International Journal of Computer Mathematics, 92, 970-979.
    https://doi.org/10.1080/00207160.2014.915960

  140. 140. Li, L., Xu, D. and Luo, M. (2013) Alternating Direction Implicit Galerkin Finite Element Method for the Two-Dimensional Fractional Diffusion-Wave Equation. Journal of Computational Physics, 255, 471-485.
    https://doi.org/10.1016/j.jcp.2013.08.031

  141. 141. Fairweather, G., Yang, X., Xu, D. and Zhang, H. (2015) An ADI Crank-Nicolson Orthogonal Spline Collocation Method for the Two Dimensional Fractional Diffusion-Wave Equation. Journal of Scientific Computing, 65, 1217-1239.
    https://doi.org/10.1007/s10915-015-0003-x

  142. 142. Cui, M. (2012) Compact Alternating Direction Implicit Method for Two-Dimensional Time Fractional Diffusion Equation. Journal of Computational Physics, 231, 2621-2633.
    https://doi.org/10.1016/j.jcp.2011.12.010

  143. 143. Zhang, Y. and Sun, Z. (2014) Error Analysis of a Compact ADI Scheme for the 2D Fractional Subdiffusion Equation. Journal of Scientific Computing, 59, 104-128.
    https://doi.org/10.1007/s10915-013-9756-2

  144. 144. Yao, W., Sun, J., Wu, B. and Shi, S. (2015) Numerical Simulation of a Class of Fractional Subdiffusion Equations via the Alternating Direction Implicit Method. Numerical Methods for Partial Differential Equations, 32, 531-547.
    https://doi.org/10.1002/num.22004

  145. 145. Wang, Y. and Wang, T. (2016) Error Analysis of a High-Order Compact ADI Method for Two-Dimensional Fractional Convection-Subdiffusion Equations. Calcolo, 53, 301-330.
    https://doi.org/10.1007/s10092-015-0150-3

  146. 146. Wang, Z. and Vong, S. (2014) A High-Order Exponential ADI Scheme for Two Dimensional Time Fractional Convection-Diffusion Equations. Computers & Mathematics with Applications, 68, 185-196.
    https://doi.org/10.1016/j.camwa.2014.05.016

  147. 147. Zhai, S., Feng, X. and He, Y. (2014) An Unconditionally Stable Compact ADI Method for Three-Dimensional Time-Fractional Convection-Diffusion Equation. Journal of Computational Physics, 269, 138-155.
    https://doi.org/10.1016/j.jcp.2014.03.020

  148. 148. Gao, G. and Sun, Z. (2015) Two Alternating Direction Implicit Difference Schemes with the Extrapolation Method for the Two-Dimensional Distributed-Order Differential Equations. Computers & Mathematics with Applications, 69, 926-948.
    https://doi.org/10.1016/j.camwa.2015.02.023

  149. 149. Gao, G. and Sun, Z. (2016) Two alternating Direction Implicit Difference Schems for Two-Dimensional Distributed-Order Fractional Diffusion Equations. Journal of Scientific Computing, 69, 506-531.
    https://doi.org/10.1007/s10915-016-0208-7

  150. 150. Wang, H. and Wang, K. (2011) An O(Nlog2N) Alternating-Direction Finite Difference Method for Two-Dimensional Fractional Diffusion Equations. Journal of Computational Physics, 230, 7830-7839.
    https://doi.org/10.1016/j.jcp.2011.07.003

  151. 151. Wang, H. and Du, N. (2014) Fast Alternating-Direction Finite Difference Methods for Three-Dimensional Space-Fractional Diffusion Equations. Journal of Computational Physics, 258, 305-318.
    https://doi.org/10.1016/j.jcp.2013.10.040

  152. 152. Tian, W., Zhou, H. and Deng, W. (2015) A Class of Second Order Difference Approximations for Solving Space Fractional Diffusion Equations. Mathematics of Computation, 294, 1703-1727.
    https://doi.org/10.1090/S0025-5718-2015-02917-2

  153. 153. Chen, M. and Deng, W. (2014) Fourth Order Accuarate Scheme for the Space Fractional Diffusion Equations. SIAM Journal on Numerical Analysis, 52, 1418-1438.
    https://doi.org/10.1137/130933447

  154. 154. Chen, M. and Deng, W. (2014) A Second-Order Numerical Method for Two-Dimensional Two-Sided Space Fractional Convection Diffusion Equation. Applied Mathematical Modelling, 38, 3244-3259.
    https://doi.org/10.1016/j.apm.2013.11.043

  155. 155. Song, F. and Xu, C. (2015) Spectral Direction Splitting Methods for Two-Dimensional Space Fractional Diffusion Equations. Journal of Computational Physics, 299, 196-214.
    https://doi.org/10.1016/j.jcp.2015.07.011

  156. 156. Liu, F., Zhuang, P., Turner, I., Anh, V. and Burrage, K. (2015) A Semi-Alternating Direction Method for a 2-D Fractional Fitz Hugh-Nagumo Monodomain Model on an Approximate Irregular Domain. Journal of Computational Physics, 293, 252-263.
    https://doi.org/10.1016/j.jcp.2014.06.001

  157. 157. Bu, W., Tang, Y., Wu, Y. and Yang, J. (2015) Crank-Nicolson ADI Galerkin Finite Element Method for Two-Dimensional Fractional FitzHugh-Nagumo Mondomain Model. Applied Mathematics and Computation, 257, 355-364.
    https://doi.org/10.1016/j.amc.2014.09.034

  158. 158. Zeng, F., Liu, F., Li, C., et al. (2014) A Crank-Nicolson ADI Spectral Method for a Two-Dimensional Riesz Space Fractional Nonlinear Reaction-Diffusion Equation. SIAM Journal on Numerical Analysis, 52, 2599-2622.
    https://doi.org/10.1137/130934192

  159. 159. Dendy, J.E. (1975) An Anlysis of Some Galerkin Schemes for the Solution of Nonlinear Time Problems. SIAM Journal on Numerical Analysis, 12, 541-565.
    https://doi.org/10.1137/0712042

  160. 160. Fernandes, R.I. and Fairweather, G. (1991) An Alternating Direction Galerkin Method for a Class of Second-Order Hyperbolic Equations in Two Space Variables. SIAM Journal on Numerical Analysis, 28, 1265-1281.
    https://doi.org/10.1137/0728067

Journal Menu>>