American Journal of Computational Mathematics
Vol.06 No.03(2016), Article ID:70402,8 pages
10.4236/ajcm.2016.63024
Calculation of the Average Irradiance and the Microalgae Growth for a Year at CUET, Bangladesh
Ismot Ara Khanam, Ujjwal Kumar Deb
Department of Mathematics, Chittagong University of Engineering & Technology, Chittagong, Bangladesh

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 June 2016; accepted 3 September 2016; published 6 September 2016
ABSTRACT
The light is one of the important factors for the microalgae growth in the biofuel technology. As biofuel project is large and expensive thus before setting a microalgae based biofuel project in any geographical location, it is important to investigate the suitability of all important parameters involving with the system. This paper aims to investigate the sunlight availability and the microalgae growth for a photobioreactor at Chittagong University of Engineering and Technology (CUET). A computational growth model related to the average irradiance is proposed to calculate the growth of microalgae. We observed that average irradiance is the highest in June and is the lowest in December. From our simulation it is found that the growth of microalgae varies with the average irradiance in a year.
Keywords:
Biofuel, Microlagae, Light Irradiance, Tubular Reactor, Simulation

1. Introduction
Continued use of petroleum based fuels is now recognized as unsustainable because of depleting energy source and these categories of fuels have unconstructive environmental affect by increasing Green House Gases (GHG). A major cause of global warming: increased concentrations of GHG. Renewable, carbon neutral, transport fuels are necessary for environmental and cost efficient sustainability [1] . The Plant based bio-fuels is a potential renewable and carbon neutral alternative to the petroleum fuels [2] . Even though most bio-fuels are still more costly than the fossil fuels, their use is increasing day by day in so many countries around the world. Encouraged by strategy measures and bio-fuels goals for transportation sector, global production of bio-fuels is estimated to be more than 35 billion liters [3] . In bio-fuel technology, some microalgae species appeared to be the only promising source of the renewable biodiesel capable of meeting the use of the fossil based fuels. The oil extraction from microalgae started during the gas supply scare in the 1970s [4] . Within a few years bio-fuels is gaining attention and the industry showed an increasing interest in microalgae production due to increase of crude-oil price. Microalgae are oxygenic photoautotrophic microorganisms. These unicellular microorganisms are very small plant―between 1 - 50 micrometers in diameter without roots or leaves. Most microalgae species use sunlight as an energy source and convert sunlight, water and CO2 into the algal biomass [5] . The high oil content of some microalgae species allows them to produce 1000 times’ oil as much as soybean grown on the same amount of land. Oil content in microalgae can exceed 80% by weight of dry biomass but oil crops, such as soybean, and palm produce oils in amounts that are miniscule compared with microalgae [6] . Microalgae need light for photosynthesis to obtain energy. The optimal temperature is between 20˚C and 24˚C for microalgae cultures [7] . Two major types of algae cultivation facilities: one is the open pond systems and another is the closed photo bioreactor systems. An open pond is made of a closed loop recirculation channel which is built in concrete or compacted earth and lined with white plastic bag. The closed photo-bioreactors are usually made of either glass or plastic transparent tubes. For microalgae production, a closed photo bioreactors (PBRs) system is considered to be better alternative than traditional open pond system for mass production and to deplete the risk of contamination by other micro-organisms and outside environment, improves microalgae growth. The success of mass production of microalgae for biodiesel significantly depends on the design and performance of the PBRs [8] [9] . Different types of PBRs are available for microalgae cultivation including tubular, Flat plat, Helical, Torus, Stirred tank, Spiral, Vertical column plastic bags etc. Tubular PBRs are the most suitable types for outdoor biomass production. The main optimal factors for microalgae growth are light, CO2, temperature and pH [10] .
The tubular photo-bioreactors consist of solar collectors, where microalgae collect energy from the sun. This is usually made of plastic or glass. The solar collector tubes are generally 0.1 m or less in diameter. Tube diameter is limited because light does not penetrate deeply. In outdoor cultivation, the ultimate source of light is the sun, which cannot be controlled. The solar collector must maximize capture of sunlight for photosynthesis [11] . To maximize sunlight capture, the solar collector tubes are always tilting North-South. The ground beneath the solar collector is either painted white or covered with white sheets of plastic to increase reflectance or albedo. A high albedo increases the total light received by the tubes. To minimize cost, the biomass must be produced using available sunlight is affected by fluctuations such as daily and seasonal variations in light levels [12] . Availability and intensity of sunlight are the most important factors controlling productivity of photosynthetic cultures of microalgae. Excessive light can be detrimental is known to produce a photo-inhibitory response. The photo-inhibitory processes are time dependent, and unalterable ruin will occur after few minutes of light stress, with cell damages exceeding 50% after 10 - 20 minutes [13] . Photosynthesis produces oxygen for the microalgae culture inside the photobioreactor. To prevent photo-inhibition and cell damage, the utmost bearable dissolved oxygen level should not exceed 400% of air saturation value. Penetration of light into the PBR influences the composition, growth rate and product formation. In order to obtain energy by photosynthesis, Microalgae require light within the Photo-synthetically Active Radiation (PAR) which is visible light radiation, spanning over a wavelength of 400 - 700 nm. In dense cultures, the gradient of light varies along the radius of the PBR because of light intensity attenuation. The attenuation of light intensity is dependent on wavelength of the light, cell concentration, geometry of PBR and the penetration distance of light. The PBR is divided into 3 zones based on different growth rates. The first zone which is the light zone extends from the illuminated wall to the point where light energy intake just balances the energy needed for growth at maximum rate. The second zone which is the peripheral zone starts thereof and extends to the point where the light energy intake just balances the energy needed for maintenance. The third zone which is the dark zone is defined as the zone where growth is negative due to limited availability of light [14] . In this paper, a mathematical model is developed to investigate the microalgae growth in response to the solar irradiance all over year at CUET, Bangladesh.
2. Basic Terminologies for Solar Radiation
For understanding the mathematical model, it is necessary to define some parameters of the solar system [15] . These are as follows in Figure 1.
2.1. Latitude
The latitude is the angular distance of the point on the earth measured north (or south) of the equator. It is the
Figure 1. The angle of incidence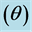 , Surface azimuth angle
, Surface azimuth angle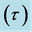 , Surface slope
, Surface slope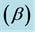 , Zenith angle
, Zenith angle , Hour angle
, Hour angle 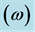 for a tilted surface.
for a tilted surface.
angle between a line from the point on the earth’s surface to the center of the earth and the projection of that line on the equatorial plane. North latitudes are positive and south latitudes are negative. The range of latitudes is given by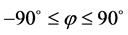 .
.
2.2. Declination Angle
The declination angle is the angular distance of the sun north (or south) of the celestial equator. It is the angle between a line extending from the center of the sun to the center of the earth and the projection of this line upon the earth’s equatorial plane. The declination is positive when the sun is north of the equator and negative when the sun is south of the equator. The declination varies from −23.45 degrees to 23.45 degrees. Around December 21, the northern hemisphere of the earth is tilted 23.45 degrees away from the sun, which is the winter solstice for the northern hemisphere and the summer solstice for the southern hemisphere. Around June 22nd, the southern hemisphere is tilted 23.45 degrees away from the sun, which is the summer solstice for the southern hemisphere. On March 22nd and September 23rd are the fall and spring equinoxes when the sunpassing directly over the equator. At the equinoxes, declination is zero. According to Cooper, The declination is calculated with the following formula:
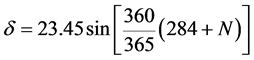 (1)
(1)
where N is the day of the year. The value of N for any day of the month can be obtained with the help of following Table 1.
2.3. Hour Angle
The hour angle is the angle measured in the earth’s equatorial plane between the projection of a line from the point on the earth’s surface to the center of the earth and the projection of a line from the center of the sun to the center of the earth. It expresses the time of the day with respect to the solar noon. At solar noon, it is zero. One hour of time is represented by  degrees of an hour angle. As part of the convention, the hour angle is negative before solar noon and positive after solar noon. It can be expressed by
degrees of an hour angle. As part of the convention, the hour angle is negative before solar noon and positive after solar noon. It can be expressed by
 (2)
(2)
Table 1. The values of the declination  and N by the Months.
and N by the Months.
where sh is the solar hour to be determined.
2.4. Zenith Angle
The zenith angle is the angle between the sun’s rays and local vertical, i.e. a line perpendicular to the horizontal plane through the point. It is denoted by 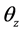
2.5. Slope of the Surface
It is the angle between the plane of the surface of the object and the horizontal. The range of slope is given by .
.
2.6. Surface Azimuth Angle
It is the angle between south and horizontal projection of the surface normal. The sign convention is used for 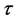 is negative for a surface that faces east of south and positive for a surface that faces west of south.
is negative for a surface that faces east of south and positive for a surface that faces west of south.
2.7. Surface Azimuth Angle
The angle of incidence is the angle between the solar rays and the surface normal. It is denoted by
3. Mathematical Model
Algal suspension in the tubular reactor is considered to be an incompressible viscous single-phase Newtonian fluid. The equations set for the incompressible fluid dynamics is used for current flow behavior i.e., 1) Continuity equation, and 2) The Navier-Stokes equation


where, r represents the density and g denotes the gravity.
The viscosity 

where is 

When cell proliferation occurs, it induces the change of algal concentration and subsequently the change of viscosity of the algal suspension. In this study, a microalgae cell is considered to be a small sphere [17] . The Einstein’s relative viscosity relating to the concentration is then used and determined by

where 


where 




where 
The equation of average irradiance:

where 


The cosine of angle of incidence can be expressed by:

For flat surface [20] , considering the surface slope β = 0, we get this simplest form of the Equation (11) as:

where 

4. Results and Discussion
The first step to calculate the microalgae growth is to calculate the Average Irradiance on a horizontal surface of a photobioreactor and to calculate the cosine of angle of incidence using Equation (12). The Average Irradiance is shown in Figure 2 on a monthly basis. For 23rd March to 20th September, the hours from 6 am to 6 pm and for the rest of the year, the hours of 7 am to 5 pm are taken into account for sunlight availability calculations. From Figure 2, it is observed that average irradiance is highest in June and lowest in December. The average irradiance is derived using parameters shown in Table 2.
In Figure 3 and Figure 4 present the graphs of cell concentration versus time (Solar Hour). In Figure 3, we found that the cell concentration of microalgae culture on the seventh day (7th April) from the morning (06:00) to the evening (18:00) increases from 1.5212 to 1.5356 kg/m3. There are almost similar scenario is depicted in Figure 4 as well. The cell concentration of the microalgae of culture on the seventh day (7th October) from the morning (06:00) to the evening (18:00) increases from 1.5218 to 1.53594 kg/m3. Therefore, a very slow increase of concentration is observed. From these results we can deduce that the growth related to concentration of microalgae is not constant but the microalgae growth varies with average irradiance of the daylight.
5. Conclusion
In this paper, the average irradiance for microalgae growth at Chittagong University of Engineering & Technology (CUET), Bangladesh is calculated throughout a year. The concentration of microalgae cell related to the growth rate is simulated by using COMSOL Multiphysics 4.2a. The declination is considered to a relation with the day of
Table 2. Parameters values for the simulation of microalgae culture.
Figure 2. Variations of average Irradiance versus time for clear sunny day at CUET.
Figure 3. Concentration of microalgae cell from 07:00 to 15:00 on the seventh day (7th April) of the culture.
Figure 4. Concentration of microalgae cell from 06:00 to 18:00 on the seventh day (7th October) of the culture.
a year. From our calculated data it was found that average irradiance is the highest in June and is the lowest in December for an entire year at CUET. It was also observed that the growth of microalgae varies with the average irradiance. It is a kind of feasible analysis for practical implementation of biofuel project at CUET. It is observed that one can take initiative to set a biofuel project from microalgae at CUET in the present available solar energy.
Acknowledgements
The authors are gratefully acknowledged for the technical supports to the Centre of Excellence in Mathematics, Mahidol University, Rama-6 Road, Bangkok, Thailand.
Cite this paper
Ismot Ara Khanam,Ujjwal Kumar Deb, (2016) Calculation of the Average Irradiance and the Microalgae Growth for a Year at CUET, Bangladesh. American Journal of Computational Mathematics,06,237-244. doi: 10.4236/ajcm.2016.63024
References
- 1. Chisti, Y. (2007) Biodiesel from Microalgae. Biotechnology Advances, 25, 294-306.
http://dx.doi.org/10.1016/j.biotechadv.2007.02.001 - 2. Smith, V.H., Sturm, B.S.M., Noyelles, F.J. and Billings, S.A. (2010) The Ecology of Algal Biodiesel Production. Trends in Ecology & Evolution (Personal Edition), 25, 301-309.
http://dx.doi.org/10.1016/j.tree.2009.11.007 - 3. Wolker, H., Maria, B., Kleinegis, D., Bosma, R.H. and Rene, W. (2011) Microalgae: The Green Gold of the Future? Wageningen UR.
- 4. Chisti, Y. (2008) Biodiesel from Microalgae Beats Bioethanol. Trends in Biotechnology, 26, 126-131.
http://dx.doi.org/10.1016/j.tibtech.2007.12.002 - 5. Bitog, J.P., et al. (2011) Application of Computational Fluid Dynamics for Modeling and Designing Photo-Bioreactors: For Microalgae Production: A Review. Computers and Electronics in Agriculture, 76, 131-147.
http://dx.doi.org/10.1016/j.compag.2011.01.015 - 6. Report: Commission of the European Communities (2006) An EU Strategy for Biofuels, 34 final, Brussels.
- 7. Molina Grima, E., Fernandez, F.G.A., Garcia Camacho, F. and Christ, Y. (1998) Photo-Bioreactors: Light Regime, Mass Transfer and Scale Up. Journal of biotechnology, 70, 231-247.
- 8. Molina, E.G. (1999) Microalgae, Mass Culture Methods. In: Flickinger, M.C. and Drew, S.W., Eds., Encyclopedia of Bioprocess Technology: Fermentation, Biocatalysis and Bioseparation, Wiley, 1753-1769.
- 9. Tredici, M.R. (1999) Photobioreactors, Encyclopedia of Bioprocess Technology: Fermentation, Biocatalysis and Bioseparation. Wiley, 1, 395-419.
- 10. Wu, L. and Song, Y.H. (2009) Numerical Investigation of Flow Characteristics and Irradiance History in a Novel Photobioreactor. African Journal of Biotechnology, 8, 4672-4679.
- 11. Teresa, M.M., Martins, A.A. and Caetano, N.S. (2010) Microalgae for Biodiesel Production and Other Applications: A Review. Renewable and Sustainable Energy Reviews, 14, 217-232.
http://dx.doi.org/10.1016/j.rser.2009.07.020 - 12. Ugwu, C.U., Aoyagi, H. and Uchiyama, H. (2008) Photobioreactors for Mass Cultivation of Algae. Bioresource Technology, 99, 4021-4028.
http://dx.doi.org/10.1016/j.biortech.2007.01.046 - 13. Pulz, O. (2001) Photobioreactors: Production Systems for Phototrophic Microorganisms. Applied Microbiology and Biotechnology, 57, 287-293.
http://dx.doi.org/10.1007/s002530100702 - 14. Molina, E., Fernandez, J., Acien F.G. and Christi, Y. (2000) Tubular Photo-Bioreactor Design for Algae Culture. Journal of Biotechnology, 92, 113-131.
- 15. Duffie, J.A. and Beckman, W.A. (1980) Solar Engineering of Thermal Process. John Wiley and Sons, New York.
- 16. Deb, U.K., Kittisak, C., Lenbury, Y. and Benchawan, W. (2012) Numerical Simulation of 2-p Laminar Flow for CO2 and Microalgae Suspension in the HLTP. Latest Adv. in Systems Science and Computational Intelligence, 53-58.
- 17. Wu, X. and Merchuk, J.C. (2004) Simulation of Algae Growth in a Bench Scale Internal Loop Airlift Reactor. Chemical Engineering Science, 59, 2899-2912.
http://dx.doi.org/10.1016/j.ces.2004.02.019 - 18. Einstein, A. (1906) Eine neue Bestimmung der Moleküldimensionen. Annalen der Physik, 19, 289-306.
http://dx.doi.org/10.1002/andp.19063240204 - 19. Deb, U.K., Chayantrakom, K. and Lenbury, Y. (2012) Comparison of Single-Phase and Two-Phase Flow Dynamics in the HLTP for Microalgae Culture. International Journal of Mathematics and Computers in Simulation, 6, 496-503.
- 20. Garcia Camacho, F., Contreras Gomez, A., Acien Fernandez, F.G., Fernandez Sevilla, J. and Molina Grima, E. (1999) Use of Concentric-Tube an Lift Photo-Bioreactors for Micro Algal Outdoor Mass Culture. Enzyme and Microbial Technology, 24, 164-172.
http://dx.doi.org/10.1016/S0141-0229(98)00103-3






