American Journal of Computational Mathematics
Vol.05 No.03(2015), Article ID:59302,6 pages
10.4236/ajcm.2015.53024
A New Analytical Study of Modified Camassa-Holm and Degasperis-Procesi Equations
Majeed A. Yousif1, Bewar A. Mahmood2, Fadhil H. Easif1
1Department of Mathematics, University of Zakho, Zakho, Iraq
2Department of Mathematics, University of Duhok, Duhok, Iraq
Email: majeed.ahmed@uod.ac, bewar.ahmed@uod.ac, dean.sic@uoz.ac
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 June 2015; accepted 28 August 2015; published 31 August 2015
ABSTRACT
In this letter, variational homotopy perturbation method (VHPM) has been studied to obtain solitary wave solutions of modified Camassa-Holm and Degasperis-Procesi equations. The results show that the VHPM is suitable for solving nonlinear differential equations with fully nonlinear dispersion term. The travelling wave solution for above equation compared with VIM, HPM, and exact solution. Also, it was shown that the present method is effective, suitable, and reliable for these types of equations.
Keywords:
Homotopy Perturbation Method, Modified Camassa-Holm Equation, Modified Degasperis-Procesi Equation

1. Introduction
Many varieties of physical, chemical, and biological phenomena can be expressed in terms of nonlinear partial differential equations. In most cases, it is difficult to obtain the exact solution for these equations. Therefore analytical methods have been used to find approximate solutions. In recent years, many analytical methods such as the Adomian decomposition method [1] [2] , the homotopy analysis method [3] [4] , the variational iteration method [5] [6] , the homotopy perturbation method [7] - [10] , and variational homotopy perturbation method [11] [12] have been utilized to solve linear and nonlinear equations.
In this paper, we will use variational homotopy perturbation method to study the Modified Camassa-Holm and Degasperis-Procesi equations and obtain their analytical solutions.
2. Mathematical Models
Wazwaz [13] studies a family of important physically equations which is called modified 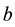 -equation. It has the following expression:
-equation. It has the following expression:
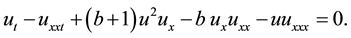 (1)
(1)
where 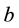 is a positive integer. As is known, when
is a positive integer. As is known, when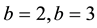 , Equation (1) reduces to modified Camassa- Holm (mCH) equation and modified Degasperis-Procesi (mDP) equation, respectively.
, Equation (1) reduces to modified Camassa- Holm (mCH) equation and modified Degasperis-Procesi (mDP) equation, respectively.
The mCH equation with exact solution [13] :
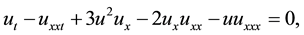 (2)
(2)
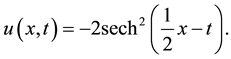 (3)
(3)
The mDP equation with exact solution [13] :
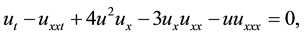 (4)
(4)
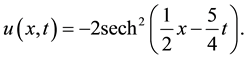 (5)
(5)
3. Analytical Methods
3.1. Variational Iteration Method (VIM)
To clarify the basic ideas of VIM, we consider the following differential equation
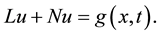 (6)
(6)
where 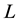 is a linear operator defined by
is a linear operator defined by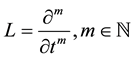 ,
, 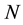 is a nonlinear operator and
is a nonlinear operator and 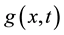 is a known analytic function. According to (VIM), we can write down a correction functional as follows:
is a known analytic function. According to (VIM), we can write down a correction functional as follows:
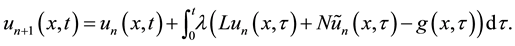 (7)
(7)
where 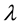 is a general lagrangian multiplier by [14] defined as:
is a general lagrangian multiplier by [14] defined as:
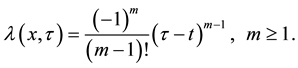 (8)
(8)
The subscript 

3.2. Homotopy Perturbation Method (HPM)
To illustrate the basic idea of this method, we consider the following nonlinear differential equation:

with the boundary condition

where 










Homotopy perturbation structure is shown as follows:

where

In Equation (12), 



and the best approximation for solution is:

It is well known that series (15) is convergent for most of the cases and also the rate of convergence depends on
3.3. Variational Homotopy Perturbation Method (VHPM)
To illustrate the concept of the variational homotopy perturbation method, we consider the general differential Equation (6). We construct the correction functional (7) and apply the homotopy perturbation method (14) to obtain:

As we see, the procedure is formulated by the coupling of variational iteration method and homotopy perturbation method. A comparison of like powers of 
4. Application of VHPM
In this section, we apply the variational homotopy perturbation method to solve mCH and mDP equations.
4.1. Application of VHPM to Modified Camassa-Holm Equation
Consider the mCH equation


To solve Equation (17), using VIM, we have the correction functional as:

where 


Applying the variational homotopy perturbation method, we have:

Substituting initial condition (18)

Comparing the coefficient of like powers of



Then


For an arbitrary 
If only the two-term approximation of Equation (15) is sufficient, then the approximate solution of Equation (17) will be expressed as:

From its expression one can see that it is also a solitary wave solution.
Remark 1. It should be remarked that the graph drawn here and approximate solution using VHPM is in excellent agreement with HPM [16] and VIM [17] .
4.2. Application of VHPM to Modified Degasperis-Procesi
Consider the mDP equation


To solve Equation (29), using VIM, we have the correction functional as:

where 


Applying the variational homotopy perturbation method, we have:

Substituting initial condition (30)

Comparing the coefficient of like powers of p, we have



Then


For an arbitrary 

From its expression one can see that it is also a solitary wave solution.
Remark 2. It should be remarked that the graph drawn here and approximate solution using VHPM is in excellent agreement with HPM [16] and VIM [17] .
5. Figures
In this section, we show the accurance of VHPM to finding analytical solution of Modified Camassa-Holm and Degasperis-Procesi equations. Also, we compare between exact and analytical solution (see Figures 1-3).
6. Conclusion
In this paper, we apply variational homotopy perturbation method to obtain the analytical solutions of Modified Camassa-Holm and Degasperis-Procesi equations. The solutions obtained by present method is compared with the exact solution. Also, it was shown that the approximation solution by VHPM had a good agreement with HPM and VIM. We observed that the method is effective for given examples and it can be applied to many other nonlinear equations.

Figure 1. The surface 

Figure 2. The surface 

Figure 3. The curve of
Acknowledgements
We thank the editor and the referee for their comments. Many thanks to University of Zakho for supporting this work.
Cite this paper
Majeed A.Yousif,Bewar A.Mahmood,Fadhil H.Easif, (2015) A New Analytical Study of Modified Camassa-Holm and Degasperis-Procesi Equations. American Journal of Computational Mathematics,05,267-273. doi: 10.4236/ajcm.2015.53024
References
- 1. Adomian, G. (1976) Nonlinear Stochastic Differential Equations. Journal of Mathematical Analysis and Applications, 55, 441-452.
http://dx.doi.org/10.1016/0022-247X(76)90174-8 - 2. Adomian, G. (1991) A Review of the Decomposition Method and Some Recent Results for Nonlinear Equations. Computers & Mathematics with Applications, 21, 101-127.
http://dx.doi.org/10.1016/0898-1221(91)90220-X - 3. Liao, S.J. (2004) On the Homotopy Analysis Method for Nonlinear Problems. Applied Mathematics and Computation, 147, 499-513.
http://dx.doi.org/10.1016/S0096-3003(02)00790-7 - 4. Abbasbandy, S. (2009) Solitary Wave Solutions to the Modified Form of Camassa Holm Equation by Means of the Homotopy Analysis Method. Chaos, Solitons and Fractals, 39, 428-435.
http://dx.doi.org/10.1016/j.chaos.2007.04.007 - 5. He, J.H. (1998) Approximate Solution of Nonlinear Differential Equations with Convolution Product Nonlinearities. Computer Methods in Applied Mechanics and Engineering, 167, 69-73.
http://dx.doi.org/10.1016/S0045-7825(98)00109-1 - 6. He, J.H. (1999) Variational Iteration Method a Kind of Non-Linear Analytical Technique: Some Examples. International Journal of Non-Linear Mechanics, 34, 699-708.
http://dx.doi.org/10.1016/S0020-7462(98)00048-1 - 7. He, J.H. (1999) Homotopy Perturbation Technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262.
http://dx.doi.org/10.1016/S0045-7825(99)00018-3 - 8. He, J.H. (2005) Application of Homotopy Perturbation Method to Nonlinear Wave Equations. Chaos, Solitons Fractals, 26, 695-700.
http://dx.doi.org/10.1016/j.chaos.2005.03.006 - 9. Rashidi, M.M., Ganji, D.D. and Dinarvand, S. (2009) Explicit Analytical Solutions of the Generalized Burger and Burger Fisher Equations by Homotopy Perturbation Method. Numerical Methods for Partial Differential Equations, 25, 409-417.
http://dx.doi.org/10.1002/num.20350 - 10. Rashidi, M.M., Freidoonimehr, N., Hosseini, A., Anwar Bg, O. and Hung, T.K. (2014) Homotopy Simulation of Nanofluid Dynamics from a Non-Linearly Stretching Isothermal Permeable Sheet with Transpiration. Meccanica, 49, 469-482.
http://dx.doi.org/10.1007/s11012-013-9805-9 - 11. Fadhil, H.E., Manaa, S.A., Bewar, A.M. and Majeed, A.Y. (2015) Variational Homotopy Perturbation Method for Solving Benjamin-Bona-Mahony Equation. Applied Mathematics, 6, 675-683.
http://dx.doi.org/10.4236/am.2015.64062 - 12. Olusola, E. (2013) New Improved Variational Homotopy Perturbation Method for Bratu-Type Problems. American Journal of Computational Mathematics, 3, 110-113.
http://dx.doi.org/10.4236/ajcm.2013.32018 - 13. Wazwaz, A.M. (2006) Solitary Wave Solutions for Modified Forms of Degasperis-Procesi and Camassa-Holm Equations. Physics Letter A, 352, 500-504.
- 14. Wu, G.C. (2013) Challenge in the Variational Iteration Method—A New Approach to Identification of the Lagrange Multi-Pliers. Journal of King Saud University—Science, 25, 175-178.
http://dx.doi.org/10.1016/j.jksus.2012.12.002 - 15. He, J.H. (1997) A New Approach to Nonlinear Partial Differential Equations. Communications in Nonlinear Science and Numerical Simulation, 2, 230-235.
http://dx.doi.org/10.1016/S1007-5704(97)90007-1 - 16. Zhang, B.-G. and Li, S.-Y. (2008) Homotopy Perturbation Method for Modified Camassa-Holm and Degasperis-Procesi Equation. Physics Letter A, 372, 1867-1872.
- 17. Yildirim, A. (2010) Variational Iteration Method for Modified Camassa-Holm and Degasperis-Procesi Equations. International Journal for Biomedical Engineering, 26, 266-272.



