American Journal of Computational Mathematics
Vol.05 No.02(2015), Article ID:56615,9 pages
10.4236/ajcm.2015.52008
Sums of Involving the Harmonic Numbers and the Binomial Coefficients
Wuyungaowa, Sudan Wang
School of Mathematical Sciences, Inner Mongolia University, Hohhot, China
Email: wuyungw@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 December 2014; accepted 22 May 2015; published 25 May 2015
ABSTRACT
Let the numbers  be defined by
be defined by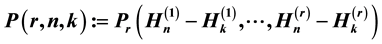 , where
, where 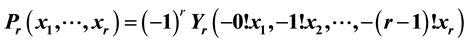 and
and  are the exponential complete Bell polynomials. In this paper, by means of the methods of Riordan arrays, we establish general identities involving the numbers
are the exponential complete Bell polynomials. In this paper, by means of the methods of Riordan arrays, we establish general identities involving the numbers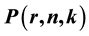 , binomial coefficients and inverse of binomial coefficients. From these identities, we deduce some identities involving binomial coefficients, Harmonic numbers and the Euler sum identities. Furthermore, we obtain the asymptotic values of some summations associated with the numbers
, binomial coefficients and inverse of binomial coefficients. From these identities, we deduce some identities involving binomial coefficients, Harmonic numbers and the Euler sum identities. Furthermore, we obtain the asymptotic values of some summations associated with the numbers 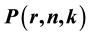 by Darboux’s method.
by Darboux’s method.
Keywords:
Harmonic Numbers, Euler Sum, Riordan Arrays, Asymptotic Values

1. Introduction and Preliminaries
Let 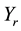 be the exponential complete Bell polynomials and
be the exponential complete Bell polynomials and
In [1] , Zave established the following series expansion:

 (1)
(1)
where  for
for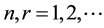 ,
,  and
and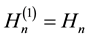 .
.
Spiess [2] introduced the numbers 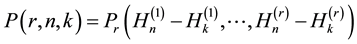 and
and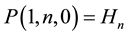 ,
,  for
for
where


The paper is organized as follows. In Section 2, we obtain some for 

involving the numbers 



Hence we write





Based on the generating function (1), we obtain the next Riordan arrays, to which we pay particular attention in the present paper:

Lemma 1 (see [5] ) Let 


2. Identities Involving the Numbers 
Theorem 1. Let



Proof. By (1), we have

Comparing the coefficients of 
Recall that 

Corollary 1. Let

Theorem 2. Let


Proof. To obtain the result, make use of the Theorem 1.
Theorem 3. Let


Proof. Applying the summation property (2) to the Riordan arrays (3), we have
which is just the desired result.
Setting 
Corollary 2 Let
Corollary 3 Let

Proof. Setting 
Corollary 4. Let
Proof. Setting 
Theorem 4. Let


Proof. which is just the desired result.
Setting 
Corollary 5. Let
Corollary 6. The substitutions 
Setting 
Corollary 7. Let
Theorem 5. Let


where 
Proof. By (1) and (2), we have
which is just the desired result.
Setting 
Corollary 8. Let
Setting 
Corollary 9. Let

We give four applications of Corollary 9:
Corollary 10. Let
3. Identities Involving 
For identities involving Harmonic numbers and inverse of binomial coefficients 
In Section, we obtain some for 

In [7] , the inverse of a binomial coefficient is related to an integral, as follows

From the generating function of 
Theorem 6. For 

Proof. From (1) and (10), we obtain
This gives (11).
Corollary 11 Setting 




Setting 
Corollary 12 The following relation holds








Corollary 13. The following relation holds




Proof. (16) minus(20) give (24); (17) minus (21), (18) minus (22) and (19) minus (23), yields (25), (26) and (27), respectively.
Leonhard Euler (1707-1783) had already stated the equation
Recall the Euler sum identities [8] [9] .
The next, we gives identities related to
For completeness we supply proofs:


Similarly, we obtain summation formulas related


By (18) and (28), (19) and (31), we have


Similarly, for completeness we supply a proof:

By (28) minus (30), we get

Applying (25) and (34), (26) and (32), we have
4. Asymptotics
Theorem 7 For 


Proof. By Lemma 1, we have
and this complete the proof.
Similarly, we can obtain the next Theorem.
Theorem 8. Let 


Theorem 9. For 


Proof. By Lemma 1, we have
this give (38).
Theorem 10. For 


Proof. By Corollary 3 of [10] , immediately complete the proof of Theorem 10.
Acknowledgements
The author would like to thank an anonymous referee whose helpful suggestions and comments have led to much improvement of the paper. The research is supported by the Natural Science Foundation of China under Grant 11461050 and Natural Science Foundation of Inner Mongolia under Grant 2012MS0118.
References
- Zave, D.A. (1976) A Series Expansion Involving the Harmonic Numbers. Information Processing Letters, 5, 75-77. http://dx.doi.org/10.1016/0020-0190(76)90068-5
- Spiess, J. (1990) Some Identities Involving Harmonic Numbers. Mathematics Computation, 55, 839-863. http://dx.doi.org/10.1090/S0025-5718-1990-1023769-6
- Brietzke, E.H.M. (2008) An Identity of Andrews and a New Method for the Riordan Array Proof of Combinatorial Identities. Discrete Mathematics, 308, 4246-4262. http://dx.doi.org/10.1016/j.disc.2007.08.050
- Wang, W. and Wang, T (2008) Generalized Riordan Arrays. Discrete Mathematics, 308, 6466-6500. http://dx.doi.org/10.1016/j.disc.2007.12.037
- Flajolet, P., Fusy, E., Gourdon, X., Panario, D. and Pouyanne, N. (2006) A Hybrid of Darboux’s Method and Singularity Analysis in Combinatorial Asymptotics. The Electronic Journal of Combinatorics, 13.
- Sofo, A. (2012) Euler Related Sums. Mathematical Sciences, 6, 10.
- Sury, B. (1993) Sum of the Reciprocals of the Binomial Coefficients. European Journal of Combinatorics, 14, 351- 353. http://dx.doi.org/10.1006/eujc.1993.1038
- Jonathan, M. (2009) Borwein and O-Yeat Chang. Duallity in Tails of Multiple-Zeta Values, 54, 2220-2234.
- David, B. and Borwein, J.M. (1995) On an Intrguing Integral and Some Series Relate to
. Proceedings of the American Mathematical Society, 123, 1191-1198.>http://html.scirp.org/file/5-1100402x159.png" class="200" />. Proceedings of the American Mathematical Society, 123, 1191-1198.
- Flajolet, P. and Sedgewick, R. (1995) Mellin Transforms Asymptotics: Finite Differences and Rice’s Integrals. Theoretical Computer Science, 144, 101-124. http://dx.doi.org/10.1016/0304-3975(94)00281-M






























 . Proceedings of the American Mathematical Society, 123, 1191-1198.>http://html.scirp.org/file/5-1100402x159.png" class="200" />. Proceedings of the American Mathematical Society, 123, 1191-1198.
. Proceedings of the American Mathematical Society, 123, 1191-1198.>http://html.scirp.org/file/5-1100402x159.png" class="200" />. Proceedings of the American Mathematical Society, 123, 1191-1198.