American Journal of Computational Mathematics
Vol.04 No.05(2014), Article ID:52614,8 pages
10.4236/ajcm.2014.45037
Accuracy and Computational Cost of Interpolation Schemes While Performing N-Body Simulations
Shafiq Ur Rehman1,2
1Department of Mathematics, The University of Auckland, Auckland, New Zealand
2Department of Mathematics, University of Engineering and Technology, Lahore, Pakistan
Email: mailto:srehman@uet.edu.pk, srehman@uet.edu.pk
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 October 2014; revised 28 November 2014; accepted 15 December 2014
ABSTRACT
The continuous approximations play a vital role in N-body simulations. We constructed three different types, namely, one-step (cubic and quintic Hermite), two-step, and three-step Hermite interpolation schemes. The continuous approximations obtained by Hermite interpolation schemes and interpolants for ODEX2 and ERKN integrators are discussed in this paper. The primary focus of this paper is to measure the accuracy and computational cost of different types of interpolation schemes for a variety of gravitational problems. The gravitational problems consist of Kepler’s two-body problem and the more realistic problem involving the Sun and four gas-giants―Jupiter, Saturn, Uranus, and Neptune. The numerical experiments are performed for the different integrators together with one-step, two-step, and three-step Hermite interpolation schemes, as well as the interpolants.
Keywords:
N-Body Simulation, Integrators, Interpolation Schemes

1. Numerical Integrators and Interpolants
Explicit Runge-Kutta-Nyström methods (ERKN) were introduced by E. J. Nyström in 1925 [1] . Here, we are using two variable-step-size ERKN integrators: Integrator ERKN689 is a nine stage, 6-8 FSAL pair [2] and ERKN101217 is a seventeen stage, 10-12 non-FSAL pair [2] . Dormand and Prince [3] and then Baker et al. [4] developed continuous approximation with embedded Runge-Kutta-Nyström methods, in which a third RKN pro- cess of order p* was used to approximate the solutions, 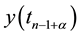 and
and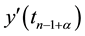 , where
, where 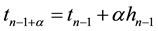 with
with 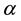 typically in (0, 1]. For ERKN101217, we used three existing interpolants: a 23-stage interpolant with
typically in (0, 1]. For ERKN101217, we used three existing interpolants: a 23-stage interpolant with , a 26-stage interpolant with
, a 26-stage interpolant with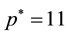 , and a 29-stage interpolant with
, and a 29-stage interpolant with . The coefficients for these interpolants are not tabulated in this paper but are freely available on-line [4] . For ERKN689, we used an 8th-order interpolant with 12 stages. The coefficients for the continuous approximation of ERKN689 were provided by P. W. Sharp (private communication).
. The coefficients for these interpolants are not tabulated in this paper but are freely available on-line [4] . For ERKN689, we used an 8th-order interpolant with 12 stages. The coefficients for the continuous approximation of ERKN689 were provided by P. W. Sharp (private communication).
For the direct numerical approximation of systems of second-order ODEs, Hairer, Nørsett and Wanner [5] developed an extrapolation code ODEX2 based on the explicit midpoint rule with order selection and step-size control. The ODEX2 integrator is good for all tolerances, especially for high arithmetic precision, for example, 10−20 or 10−30. For ODEX2 integrator we used the built-in interpolant.
Störmer methods are an important class of numerical methods for solving systems of second-order ordinary differential equations. Störmer methods were introduced by Störmer [6] . These methods have long been utilized for accurate long-term simulations of the solar system [7] . Grazier [8] recommended a fixed-step-size Störmer method of order 13 that used backward differences in summed form, summing from the highest to lowest differences. In this paper we consider an order-13, fixed-step-size Störmer method and refer to it as the 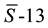 integrator.
integrator.
1.1. Hermite Interpolation Schemes
Hermite interpolation uses derivative and function values and is named after Charles Hermite (1822-1901). We used four schemes: one-step (cubic and quintic Hermite), two-step and three-step Hermite interpolation schemes. The cubic Hermite interpolation polynomial is of degree 3, while the quintic, two-step and three-step Hermite interpolation polynomials are of degrees 5, 8 and 11, respectively. The interpolation schemes are derived using a Newton divided difference approach, which is described in Section 1.1.1. There is a second approach, which we call the direct approach that is frequently used by other researchers; for example, see [9] . This approach is particularly suited for cubic and quintic Hermite interpolation schemes, and we describe it in Sections 1.1.2 and 1.1.3.
1.1.1. Newton Divided Difference Approach
To determine the interpolating polynomial 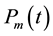 for the m points
for the m points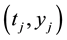 ,
, 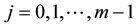 , using the Newton divided difference (NDD) approach, we write
, using the Newton divided difference (NDD) approach, we write 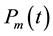 as
as
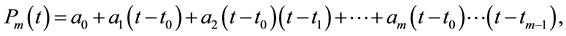
where the a’s are calculated from the divided differences. The ith divided difference can be calculated using
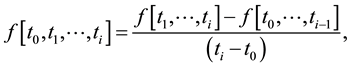
see Table 1. We now discuss how the NDD must be modified when derivative values are used. Let us consider the first-order differences in Table 1. For example, if 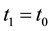 then we have
then we have
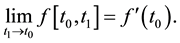
Similarly, for the second-order differences in Table 1, if, for example, 
Hence, for Hermite interpolation schemes we can use the NDD approach if the derivatives replace the corresponding divided differences.
1.1.2. Cubic Hermite Interpolation
In this section and the next, we describe the direct approach for obtaining the cubic and quintic Hermite polynomials. The cubic Hermite interpolation polynomial 






Table 1. An illustrative Newton divided difference table.
where,
and 



1.1.3. Quintic Hermite Interpolation
The quintic Hermite interpolation polynomial 







where,
and 




1.1.4. Two-Step Hermite Interpolation Polynomial
The two-step Hermite interpolation polynomial 








where the coefficients




1.1.5. Three-Step Hermite Interpolation Polynomial
Similarly, the three-step Hermite interpolation polynomial interpolates the data








As for the two-step Hermite interpolation polynomial, the coefficients





We compared the maximum error in position and the CPU-time for P3 and P5 evaluated using NDD and the direct approach. The comparison was done for one period of Kepler problem for eccentricities of 0.05 to 0.9 (see Section 2.1 for more details on the experiment), and the Jovian problem [10] .
For the two-body problem, no significant differences in the maximum error as CPU-time were observed between these two approaches. For the Jovian problem, the direct approach takes approximately half the CPU-time of the NDD approach. The coefficients of the polynomial for the NDD approach depend on the components of the solution vector. For the direct approach the coefficients are independent of the components, so they can be used as a vector to approximate polynomials and that will save CPU-time.
In the rest of the paper, cubic and quintic Hermite interpolation schemes are implemented using the direct approach. For two-step and three-step Hermite interpolation schemes we implemented the NDD approach, because it is really difficult to find the coefficients for the direct approach.
2. Numerical Experiments
Here, we examine the error growth in the position and velocity for the Kepler problem. The experiments for short-term integrations are performed using four different types of interpolation schemes applied to the Kepler problem over the interval of 2π.
2.1. Kepler Problem with Different Eccentricities
The solution to the Kepler problem is periodic with period 2π. We do not have to calculate the reference solution, so the Kepler problem is well suited for testing the accuracy of integration over a short time interval. This assumes the step-size is chosen so that 
The error in the position and velocity of the Kepler problem is given by the L2-norm
where 



The graphs in Figure 1 are for experiments performed with the cubic, quintic, two-step, and three-step Hermite interpolation schemes applied to the Kepler problem over the interval 
From Figure 1, we observe a clear pattern; as the eccentricity increases, the maximum error in the position also increases. The variation in the error is understandable, because the error depends upon the eccentricity. To illustrate this fact, recall that the analytical solution to the Kepler problem is given by

Figure 1. The maximum global error in position for the cubic, quintic, 2-step, and 3-step Hermite interpolation schemes against different eccentricities applied to the two-body problem over a period of 2π.
Table 2. The maximum global error in position for eccentricity 0.05 attained by different interpolation schemes applied to the Kepler problem over the interval [0, 2π] with four choices of numbers of evenly spaced sub-intervals. The dash means the combination is not used.
where 

y1-component of this solution can be written as
It is clear that these and all subsequent derivatives are expected to involve the factor

As mentioned earlier, the same sets of experiments described in Figure 1, were also done with different numbers of sub-intervals. We experimented with 17, 79, 255, and 1080 evenly spaced sub-intervals over the interval


The results in Table 2 show reasonably good agreement with the expected values calculated from the orders of the polynomial, discounting the possible increase in round-off error from using a higher-order interpolation scheme and a large number of sub-intervals. For example, using the cubic Hermite interpolation scheme, and going from 17 to 79 sub-intervals, the expected value is 
From Table 2 we find that the accuracy for a given interpolation scheme improves if the number of sub-in- tervals increases. We also deduce from Table 2 that it makes no sense to use any of the four interpolation schemes with ODEX2 if the required maximum global error is 10−15 and 17 sub-intervals are used. For 79 sub- intervals (used for ERKN101217) only the 2-step and 3-step Hermite interpolation schemes achieve the required accuracy. Similarly, for ERKN689, the quintic and 2-step interpolation schemes achieve the required accuracy, whereas for the 
2.2. Computational Cost of Interpolation Schemes
Let us now consider the CPU-time by looking at individual interpolation schemes. Our expectation, at least for the interpolation schemes, is that the CPU-time is proportional to the number of multiplications. If one interpolation scheme uses twice as many multiplications then the CPU-time is expected to be twice as large. There will not be many divisions, and the number of subtractions and additions is typically proportional to the number of multiplications. Normally, when timing a program, an overhead is introduced. Therefore, care has been taken not to include such overheads in the final results. We also checked reproducibility of the results and observed a maximum variation of not more than 2.5%.
As discussed earlier, there are two different approaches to form interpolation schemes. Here, the experiments are performed using a direct approach for cubic and quintic Hermite interpolation, and the Newton divided difference approach for 2-step and 3-step Hermite interpolation schemes. In most cases, interpolation schemes are split into two subroutines, one for finding the coefficients and one for evaluating the polynomials. For ERKN689 and ERKN101217, with the interpolants we have additional stage derivatives (function evaluations). Overall, we have three different groups of interpolation schemes:
1) For cubic and quintic Hermite interpolation schemes, we evaluate the coefficients of the polynomial, which are independent of the components, and the polynomial as one subroutine.
2) For 2-step and 3-step Hermite interpolation schemes, we have two subroutines:
a) The calculation of the coefficients by forming a Newton divided difference table;
b) The evaluation of the polynomial.
3) For the interpolants, we have three subroutines:
a) The evaluation of the coefficients
b) The evaluation of the additional stage derivatives;
c) The evaluation of the polynomial using a) and b).
For ODEX2, the pieces of information required to form the interpolant are considered part of the integration, and we only consider the evaluation of the polynomial; see Table 5.
Since the coefficients of the polynomials for cubic and quintic interpolations are independent of the components, the experiments for these interpolation schemes are performed as one unit. As can be seen from the formulae in Sections 1.1.2 and 1.1.3, the quintic Hermite interpolation scheme uses approximately 93% more multiplications than cubic Hermite interpolation when applied to the Jovian problem. When we did our experiment, we found that the quintic Hermite interpolation scheme uses approximately 96% more CPU-time than cubic Hermite interpolation, which is in good agreement with the expected value.
Table 3 shows the CPU-time for finding the stage derivatives of the pairs (without the cost of additional stage derivatives) used in ERKN689 and ERKN101217 when applied to the Jovian problem. With ERKN689 we use the property FSAL (first same as last), so that we need only 8 derivative evaluations per step. Similarly, the 12-stage interpolant has effectively 11 stage derivatives. Observe from Table 3 that the average CPU-time consumed per stage is approximately 8.74 × 10−07 and 8.71 × 10−07 for ERKN689 and ERKN101217, respectively. Therefore, the expected CPU-time for ERKN689 with a 12-stage interpolant is approximately 9.61 × 10−06. For ERKN101217, the expected CPU-time for finding coefficients is approximately 2.00 × 10−05, 2.26 × 10−05, and 2.52 × 10−05 with 23-stage, 26-stage, and 29-stage interpolants, respectively.
Table 4 gives the CPU time needed to find the coefficients of the interpolation schemes and evaluate all the derivatives for the interpolants when solving the Jovian problem. We observe that all values in Table 4 have reasonably good agreement with the prescribed values for CPU-time. Note also that the 3-step Hermite interpolation scheme in Table 4 uses approximately 96% more multiplications than the 2-step Hermite interpolation scheme, which is reasonably well matched by our finding of 93%.
Table 5 shows the CPU-time for evaluating the position and velocity components using the different interpolation polynomials. The 3-step interpolation scheme uses approximately 76% more CPU-time than the 2-step interpolation, which is again in agreement with the CPU-times observed in Table 4. Similarly, the difference in
Table 3. The CPU-time in seconds for evaluating the stage derivatives (without the cost of additional function evaluations) for ERKN689 and ERKN101217 applied to the Jovian problem.
Table 4. The CPU-time in seconds for finding the coefficients of the interpolation schemes and evaluating all the stage derivatives of the interpolants applied to the Jovian problem.
Table 5. The CPU-time in seconds for evaluating the position and velocity polynomials using different interpolation polynomials applied to the Jovian problem.
CPU-time between the 23-stage and 29-stage interpolants is twice the difference between the 23-stage and 26- stage interpolants which is in good agreement with the difference observed in Table 4.
3. Summary
The primary objective of this paper was to discuss the accuracy and computational cost of different interpolation schemes while performing N-body simulations. The interpolation schemes play a vital role in these kinds of simulations. We constructed three different types, namely, one-step (cubic and quintic Hermite), two-step and three-step Hermite interpolation schemes. For short-term simulations, we investigated the performance of these interpolation schemes applied to the Kepler problem over the interval [0, 2] for eccentricities in the range [0.05, 0.9]. We observed that the maximum error in position was monotonically increasing as a function of eccentricity. For a given number of sub-intervals we used in this paper, the higher-order interpolation schemes achieve better accuracy and for a given interpolation scheme the accuracy improves if the number of sub-intervals is increased. We also investigated the CPU-time by looking at individual interpolation schemes. Our expectation, at least for the interpolation schemes, was that the CPU-time was proportional to the number of multiplications. For example, the quintic Hermite interpolation scheme uses approximately 93% more multiplications than cubic Hermite interpolation when applied to the Jovian problem. When we did our experiment, we found that the quintic Hermite interpolation scheme used approximately 96% more CPU-time than cubic Hermite interpolation, which was in good agreement with the expected value. We also checked reproducibility of the results and observed a maximum variation of not more than 2.5%.
Acknowledgements
The author is grateful to the Higher Education Commission (HEC) of Pakistan for providing the funding to carry out this research. Special thanks go to Dr. P. W. Sharp and Prof. H. M. Osinga for their valuable suggestions, discussions, and guidance throughout this research.
Cite this paper
Shafiq UrRehman,11, (2014) Accuracy and Computational Cost of Interpolation Schemes While Performing N-Body Simulations. American Journal of Computational Mathematics,04,446-454. doi: 10.4236/ajcm.2014.45037
References
- 1. Nyström, E.J. (1925) Über die numerische Integration von Differentialgleichungen. Acta Societatis Scientiarum Fennicae, 50, 1-54.
- 2. Dormand, J., El-Mikkawy, M.E.A. and Prince, P. (1987) Higher Order Embedded Runge-Kutta-Nyström Formulae. IMA Journal of Numerical Analysis, 7, 423-430.
http://dx.doi.org/10.1093/imanum/7.4.423 - 3. Dormand, J.R. and Prince, P.J. (1987) New Runge-Kutta Algorithms for Numerical Simulation in Dynamical Astronomy. Celestial Mechanics, 18, 223-232.
http://dx.doi.org/10.1007/BF01230162 - 4. Baker, T.S., Dormand, J.R. and Prince, P.J. (1999) Continuous Approximation with Embedded Runge-Kutta-Nyström Methods. Applied Numerical Mathematics, 29, 171-188.
http://dx.doi.org/10.1016/S0168-9274(98)00065-8 - 5. Hairer, E., Nørsett, S.P. and Wanner, G. (1987) Solving Ordinary Differential Equations I: Nonstiff Problems. Springer-Verlag, Berlin.
- 6. Störmer, C. (1907) Sur les trajectoires des corpuscles électrisés. Acta Societatis Scientiarum Fennicae, 24, 221-247.
- 7. Grazier, K.R., Newman, W.I., Kaula, W.M. and Hyman, J.M. (1999) Dynamical Evolution of Planetesimals in Outer Solar System. ICARUS, 140, 341-352.
http://dx.doi.org/10.1006/icar.1999.6146 - 8. Grazier, K.R. (1997) The Stability of Planetesimal Niches in the Outer Solar System: A Numerical Investigation. Ph.D. Thesis, University of California, Berkeley.
- 9. Grazier, K.R., Newman, W.I. and Sharp, P.W. (2013) A Multirate Störmer Algorithm for Close Encounters. The Astronomical Journal, 145, 112-119.
http://dx.doi.org/10.1088/0004-6256/145/4/112 - 10. Rehman, S. (2013) Jovian Problem: Performance of Some High-Order Numerical Integrators. American Journal of Computational Mathematics, 3, 195-204.
http://dx.doi.org/10.4236/ajcm.2013.33028






















