American Journal of Computational Mathematics
Vol.04 No.04(2014), Article ID:49502,5 pages
10.4236/ajcm.2014.44027
A Semi Analytic Approach to Coupled Boundary Value Problem
Nityanand P. Pai, Nagaraj N. Katagi
Department of Mathematics, Manipal Institute of Technology, Manipal University, Manipal, India
Email: nppaimit@yahoo.co.in, nnkatagi@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 July 2014; revised 2 August 2014; accepted 15 August 2014
ABSTRACT
The present problem is considered as a coupled boundary value problem and is analyzed using a semi analytic method. A series method is used to obtain the solution and region of validity is extended by suitable techniques. In this case of series solution the results obtained are better than pure numerical findings up to moderately large Reynolds numbers. The variation of physical parameters is discussed in detail.
Keywords:
Suction, Coupled Equations, Analytic Continuation, Physical Parameters, Reynolds Numbers

1. Introduction
The flow between porous discs has been studied by several authors. As in the case of porous pipes and porous channels, the governing equation reduces to a set of nonlinear ordinary differential equations. This problem was first studied by Batchelor [1] who generalized the solution of Von Karman [2] . Further this problem was analyzed by Stewartson [3] who obtained perturbation solution for the small Reynolds number. Flow between a rotating and a stationary disc has been studied by Phan-Thein and Bush [4] . The problem of suction of viscous in incompressible fluid through a rotating porous disc onto a rotating co-axial disc was studied by C. Y. Wang [5] . Here we view this problem as a coupled nonlinear boundary value problem.
In the present paper we have used semianalytical numerical technique to understand the effect of suction represented by a pair of nonlinear differential equations. For simple geometrics the semianalytical numerical methods proposed here provide better results. Van Dyke [6] and his associates have successfully used these series methods in unveiling important features of various types of fluid flows. Bujurke and Pai [7] has discussed similar geometrical problem with injection at the discs.
Recently in the analysis of flow in pipe, Pai and Katagi [8] have used series analysis satisfactorily. The physical problem considered in this paper is of great importance in Fluid Dynamics. The present study is a possible extension work of Wang [5] . The problem is solved using a special type of series. The series so generated has limited utility due to presence of a singularity and its region of validity is extended by analytic continuation.
2. Mathematical Formulation
As shown in the Figure 1 we denote the spacing between the discs by 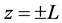 and rotating with the same angular velocity Ω. Fluid is withdrawn from both discs with velocity W. We shall assume the gap with 2L is small compared to diameter of the discs. So that end effects can be neglected. The flow field is symmetric about the
and rotating with the same angular velocity Ω. Fluid is withdrawn from both discs with velocity W. We shall assume the gap with 2L is small compared to diameter of the discs. So that end effects can be neglected. The flow field is symmetric about the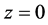 .
.
The governing equations are
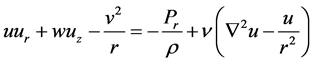 (1.1)
(1.1)
 (1.2)
(1.2)
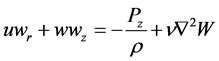 (1.3)
(1.3)
 (1.4)
(1.4)
where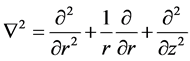 , and u, v, w are velocity components. The boundary conditions are at
, and u, v, w are velocity components. The boundary conditions are at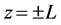 ,
,  ,
, 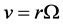 ,
,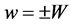 .
.
For similarity transformation we consider Wang [5]
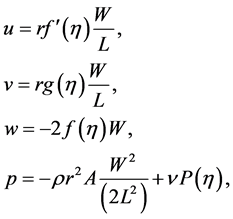 (1.5)
(1.5)
where 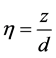 and A is constant. Now the equations take the form
and A is constant. Now the equations take the form
Figure 1. The co-ordinate system.

or
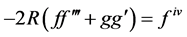 (1.6)
(1.6)


Here 


3. Method of Solution
We assume the solution of (1.6) and (1.7) in the forms


Substituting (3.1), (3.2) in (1.6) and (1.7) and comparing powers of R one can get


The relevant boundary conditions are
The solutions are
The slow convergence of series (3.1), (3.2) requires large number of terms for obtaining the approximate sum. For higher order approximations we proceed by the following scheme.
We propose a systematic scheme for this purpose, we consider 



We substitute (3.5), (3.6) in (3.3), (3.4) respectively and equate various powers of 


where







For the radial velocity profile,

Figure 2. Domb sykes plot.
Table 1. Comparison of values for
Table 2. Comparison of values for
And we have

4. Conclusions
A new type of series is presented for studying the problems of flow between the two discs using recurrences (3.7) and (3.8). In this process we generate universal coefficients


These coefficients in turn give universal coefficients for





References
- Batchelor, G.K. (1951) Note on Class of Solution of Navier-Stockes Equations Representing Symmetric Flow. Quarterly Journal of Mechanics Applied Mathematics, 4, 29-35. http://dx.doi.org/10.1093/qjmam/4.1.29
- Van Karman, T. (1921) Laminare and Turbulent Reibung. Zeitschrift für Angewandte Mathematik und Mechanik, 1, 233-241. http://dx.doi.org/10.1002/zamm.19210010401
- Stewertson, K. (1953) On the Flow between Two Rotating Discs. Proceedings of the Cambridge Philosophical Society, 49, 233-340.
- Phan Thein, N. and Bush, M.B. (1984) On the Steady Flow of a Newtonian Fluid between the Parallel Disk. Zeitschrift für Angewandte Mathematik und Physik, 35, 912-919. http://dx.doi.org/10.1007/BF00945453
- Wang, C.Y. (1986) Symmetric Viscous Flow between Two Rotating Porous Disc. Quarterly of Applied Mathematics, 4, 29-37.
- Van Dyke, M. (1974) Analysis and Improvement of Perturbation Series. Quarterly Journal of Mechanics Applied Mathematics, 27, 423-456. http://dx.doi.org/10.1093/qjmam/27.4.423
- Bujurke, N.M. and Pai, N.P. (1995) Computer Extended Series Solution to Viscous Flow between Rotating Discs. Proceedings of the Indian Academy of Sciences (Mathematical Sciences), 105, 353-369. http://dx.doi.org/10.1007/BF02837202
- Pai, N.P. and Katagi, N.N. (2013) Semi Numerical Solution for a Boundary Value Problems. American Journal of Computational Mathematics, 3, 43-47. http://dx.doi.org/10.4236/ajcm.2013.31006













