ABSTRACT

In this paper, we provide a maximum norm analysis of an overlapping Schwarz method on nonmatching grids for a quasi-variational inequalities related to ergodic control problems studied by M. Boulbrachène [1], where the “discount factor” (i.e., the zero order term) is set to 0, we use an overlapping Schwarz method on nonmatching grid which consists in decomposing the domain in two sub domains, where the discrete alternating Schwarz sequences in sub domains converge to the solution of the ergodic control IQV for the zero order term. For 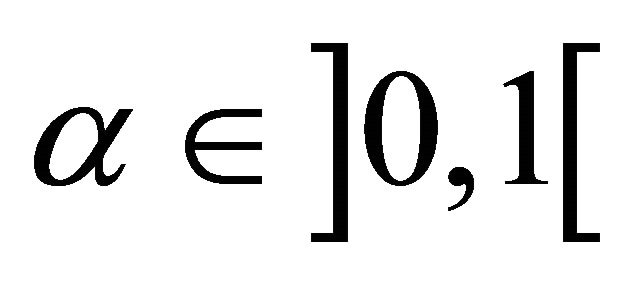and under a discrete maximum principle we show that the discretization on each sub domain converges quasi-optimally in the 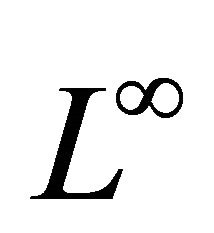norm to 0.

1. Introduction

The Schwarz alternating method can be used to solve elliptic boundary value problems on domains which consist of two or more overlapping sub domains.

The solution is approximated by an infinite sequence of functions which results from solving a sequence of elliptic boundary value problems in each of the sub domain.

In this paper, we are interested in the error analysis in the maximum norm for the obstacle problem in the context of overlapping nonmatching grids: we consider a domain Ω which is the union of two overlapping subdoains where each sub domain has its own triangulation. This kind of discretizations is very interesting as they can be applied to solving many practical problems which cannot be handled by global discretizations. They are earning particular attention of computational experts and engineers as they allow the choice of different mesh sizes and different orders of approximate polynomials in different sub domains according to the different properties of the solution and different requirements of the practical problems.

We study a new approach for the finite element approximation for the ergodic problem where the obstacle is related to a solution. We consider a domain which the union of two overlapping sub-domains where each sub domain has its own generated triangulation. The grid points on the sub-domain boundaries need not much the grid points from the other sub-domains. Under a discrete maximum principle, we show that the discretization on each sub-domain converges quasi-optimally in the 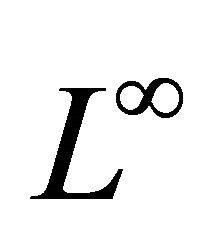norm.

In the first section we study the Schwarz method for the ergodic control Quasi-variational inequalities; we state the continuous alternating Schwarz sequence for quasivariational inequalities, and define their respective finite element counterparts in the context of overlapping grids.

In Section 2, we give a simple proof for the main result concerning error estimates in the 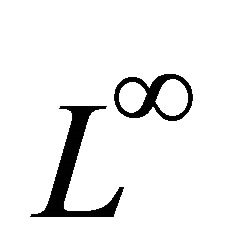norm for the problem studied, taking into account the combination of Jinping Zeng & Shuzi Zhou [2] geometrical convergence and P. L. Lions, B. Perthame [3] quasi-variational inequalities and ergodic impulse control.

2. Schwarz Method for the Ergodic Control Quasi-Variational Inequalities

We begin by down a classical results related to ergodic control quasi-variational inequalities [1-18].

It is well known that impulse control problems for reflected diffusion process may be solved by considering the solution of quasi variational inequalities (QVI) (see Bensoussan [4], A. Bensoussan and J. L. Lions [5]). A typical example is the following:

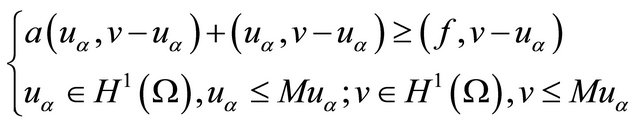(1)

where Ω is given bounded smooth open set in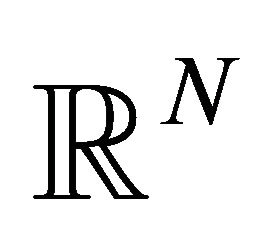, , 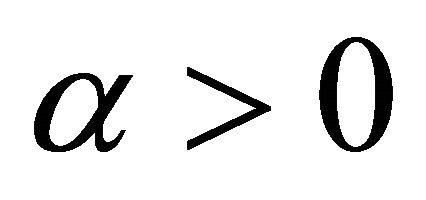f is given function, the cost function 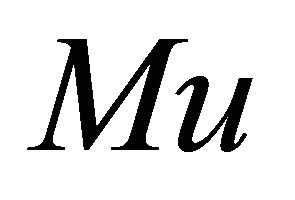represents the obstacle of impulse control defined by:

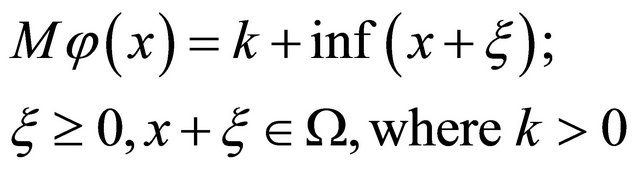(2)

where k is a positive number, M is an operator defined on 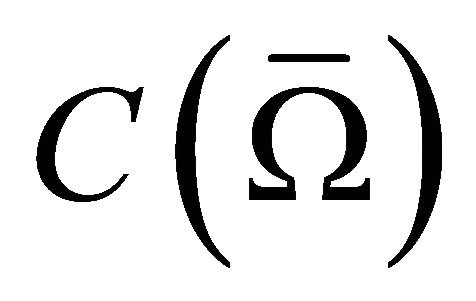and assumed to map into itself, that is,

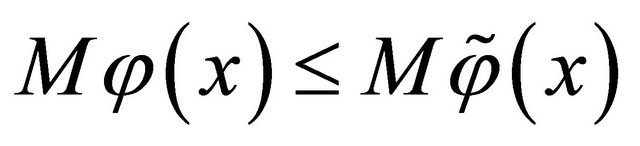whenever  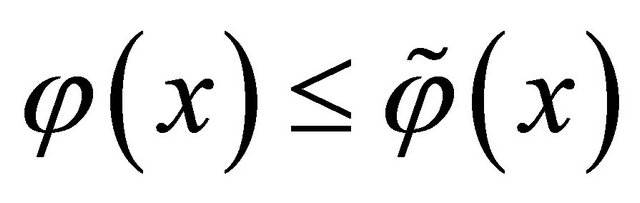  (3)

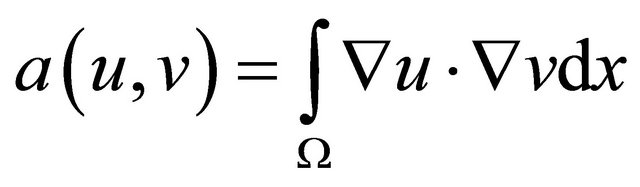; and (.,.) denotes the inner product on Ω.

It has been proved that the long run average cost for this problem solves the ergodic QVI. More precisely, denoting by:

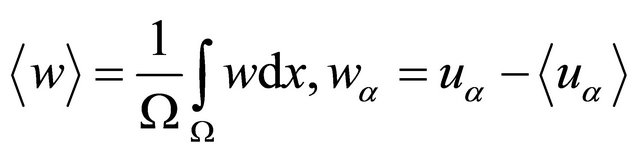and.

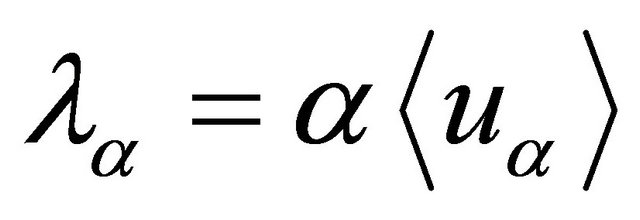P. L. Lions and B. Perthame [3] proved that the solution 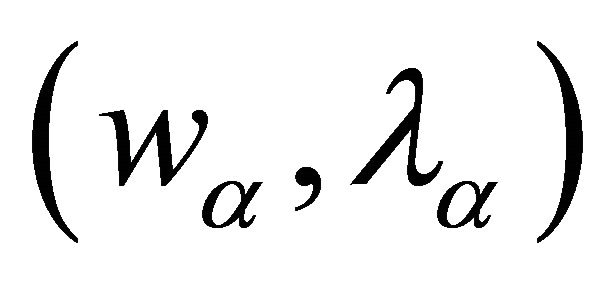of the QVI :

(4)

converges to the solution of the ergodic control QVI :

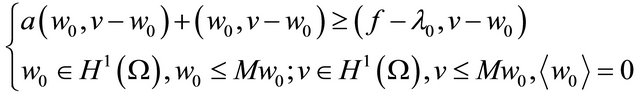
(5)

As stated in the following theorem.

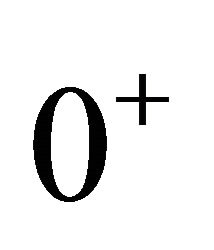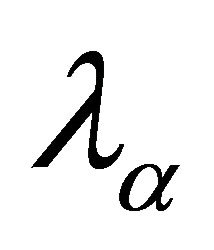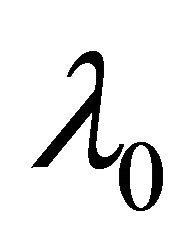Theorem 1 [1]: As goes to, converges uniformly in to some constant, and 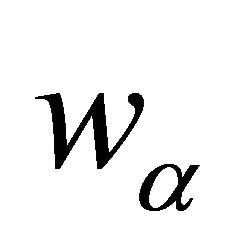converges uniformly in 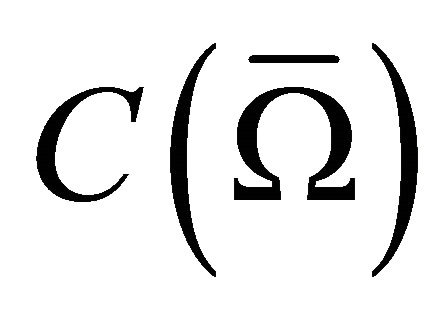and strongly in 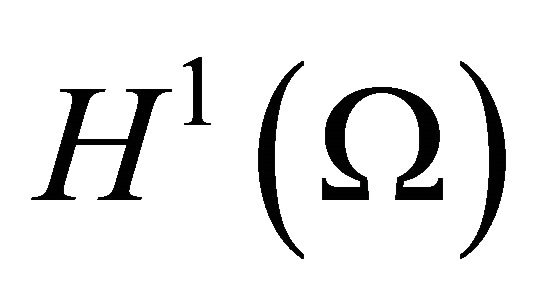to. Moreover is the unique solution of the quasi variational inequality of the ergodic control problem (5).

Problem Position

Let 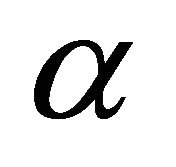be fixed in the open interval 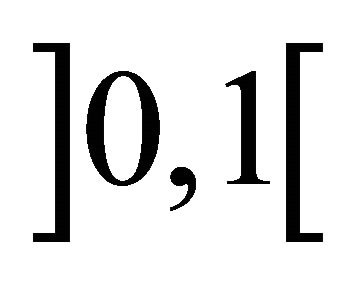and set. Then, one can easily see that problem (1) is equivalent to the following QVI:

(6)

where

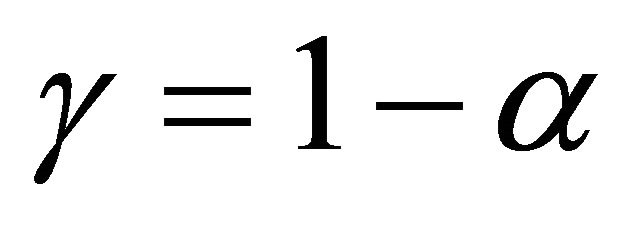, and        (7)

Thanks to [5], (1) or (6) has a unique solution. Also, notice that, as the bilinear form (7) is independent of, the left hand side of (6) is independent of 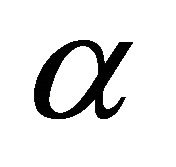too.

3. The Schwarz Method for the Obstacle

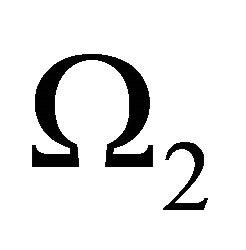We decompose into two overlapping polygonal sub domains and, such that

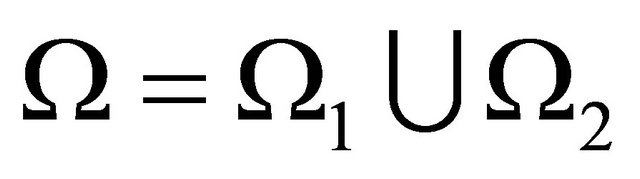(8)

and satisfies the local regularity condition

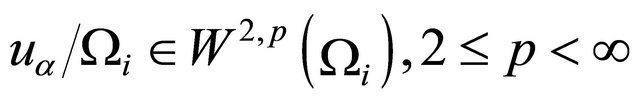(9)

We denote by 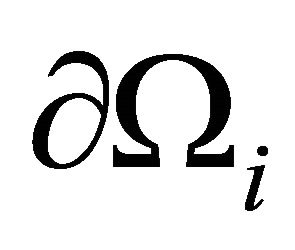the boundary condition of and 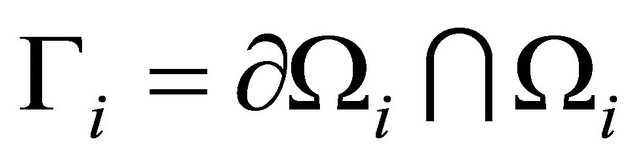the intersection of and is assumed to be empty.

3.1. The Schwarz Sequences for Problem (4)

We denote by:

and (10)

Choosing 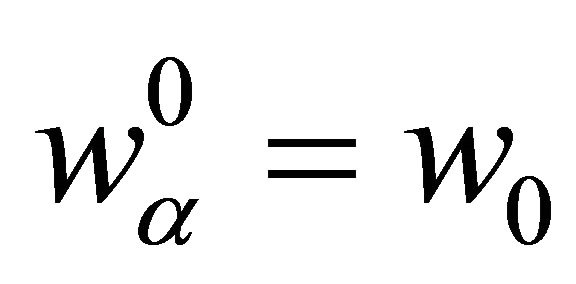such that 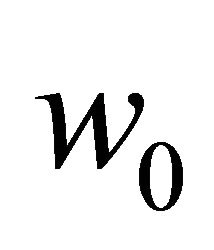the unique solution of:

(11)

We respectively define 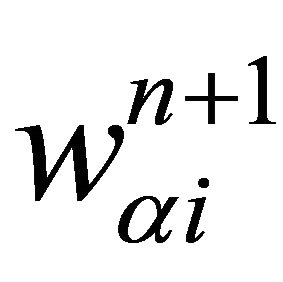the alternating Schwarz sequences on such that:

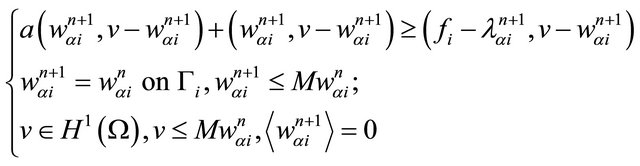
(12)

where.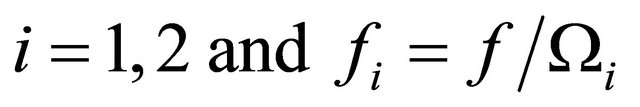

3.2. The Continuous Schwarz Sequences for Principal Problem

We consider the following problem:

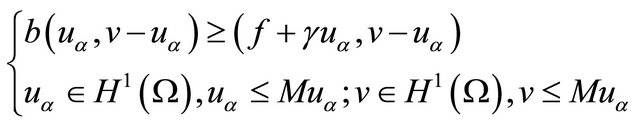(13)

Choosing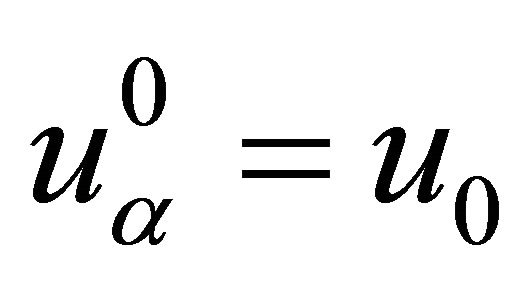, solution of:

(14)

We respectively define the alternating Schwarz sequences 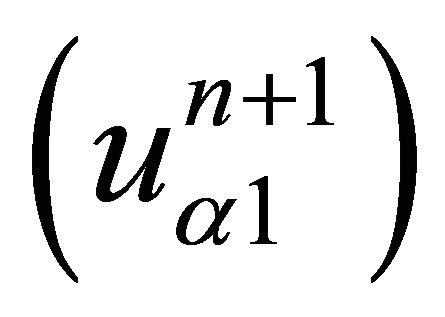on such that: 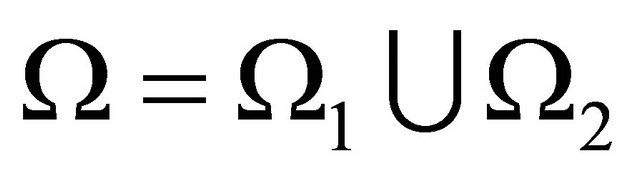and;

(15)

(16)

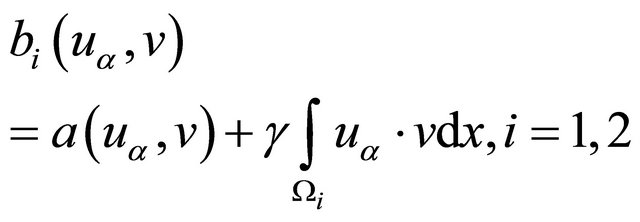(17)

Lemma 1 [3]: for each

4. The Discret Problem

We suppose for simplicity that is polyhedral. Let be a regular, quasi uniform triangulation of into nsimplexes of diameter less than h.

We denote by 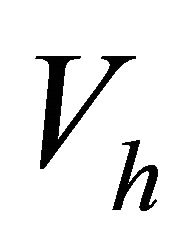the standard piecewise linear finite element espace, we consider the discrete variational inequality:

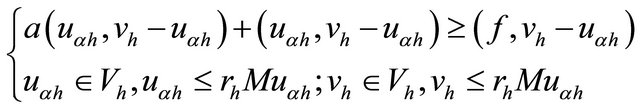(18)

Thanks to ([6]), QVI (18) has a unique solution.

4.1. The Discrete Maximum Principle [7]

We assume that the matrix A with generic coefficient is a M-matrix.

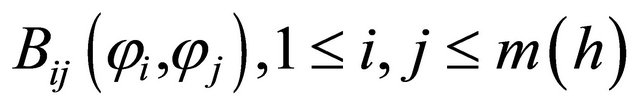(19)

As for the continuous problem, it is easy to see that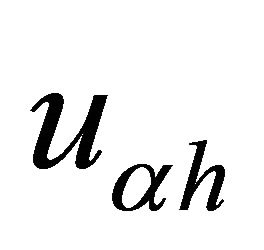, the solution of (18), is also solution to the following (QVI):

(20)

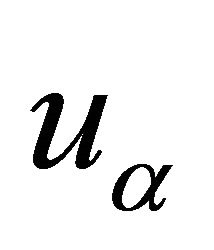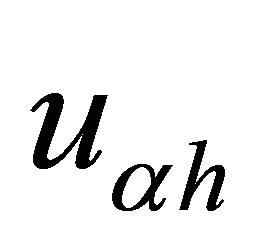Theorem 2 [1]: Let and (the discrete solution). Then, there exists a constant independent of 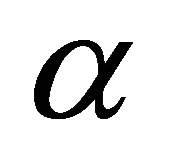the both and h such that

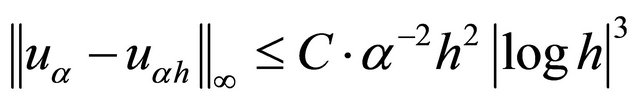
Theorem 3 [1]: Under conditions of theorem 1 and 2, we have

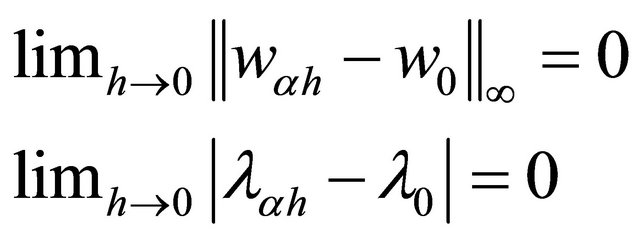
Note that 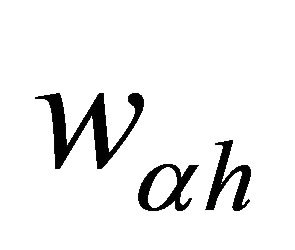and 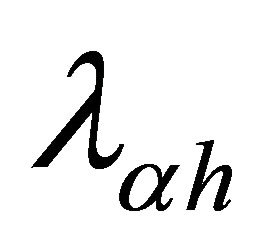is the finite element approximation of and 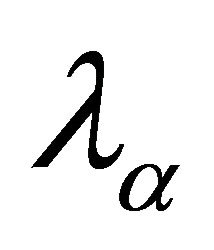respectively. 

4.2. The Discrete Schwarz Sequences

Let 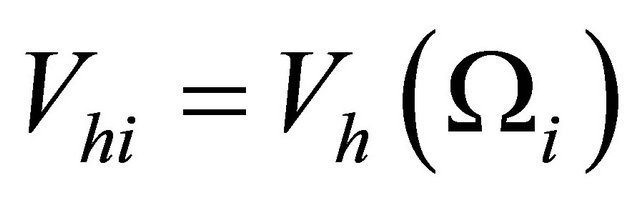be the space of continuous piecewise linear function on which vanish on.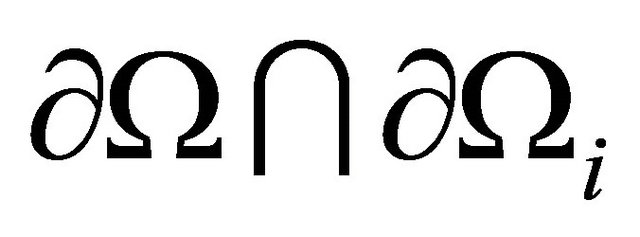

For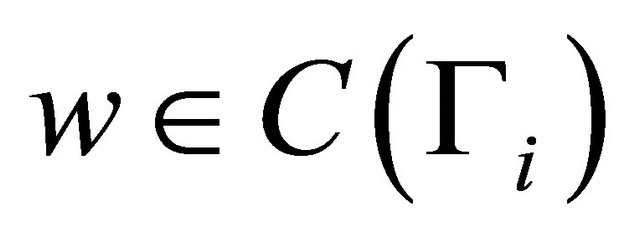, we define

where denotes the interpolation operator on.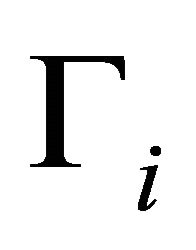

For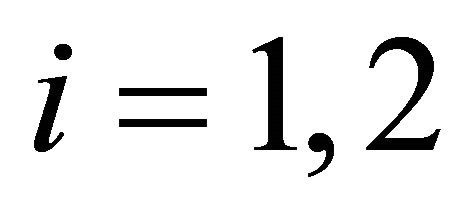. Let 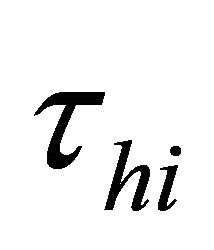be a standard regular finite element triangulation in, being the mesh size.

We suppose that the two triangulations are mutually independent on a triangle belonging to one triangulation does not necessarily belong to the other.

Choosing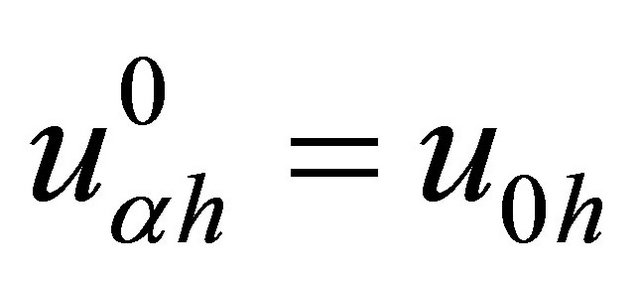, such that 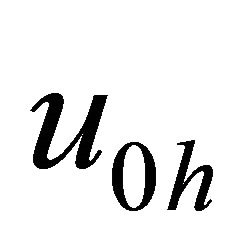is a solution of the following inequation:

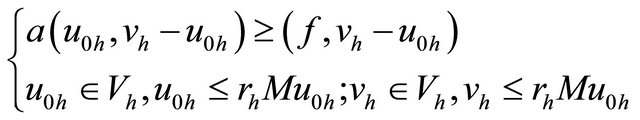(21)

We define the alternating Schwarz sequences 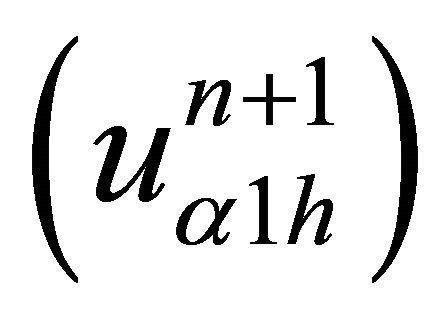on such that:

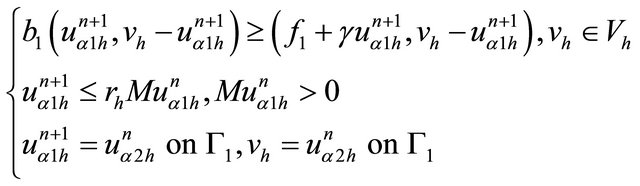(22)

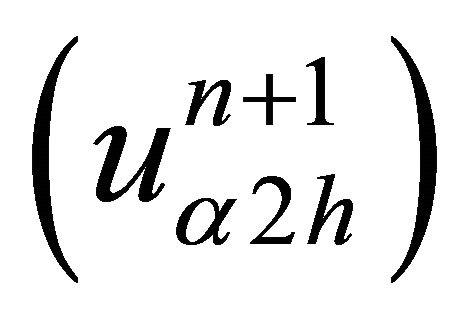And on 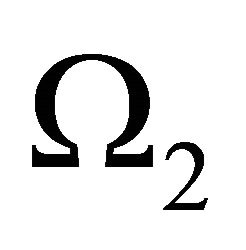such that:

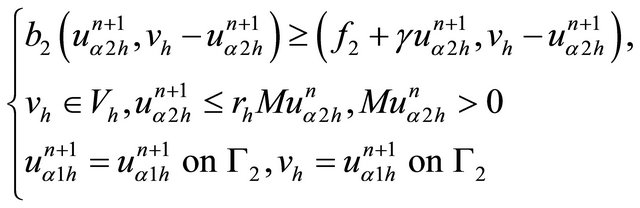(23)

Notation: We will adapt the following notations:

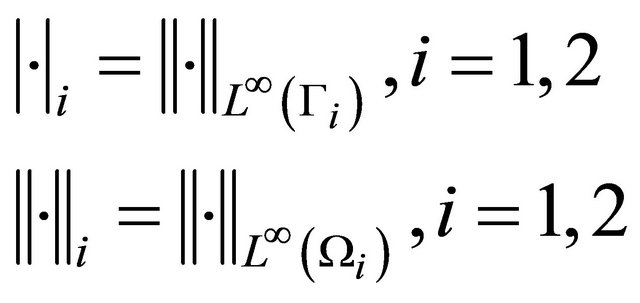(24)

5. -Error Analysis

Lemma 2 [8]: is M-matrix such that

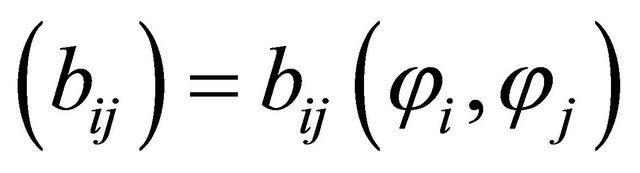
then exists constants 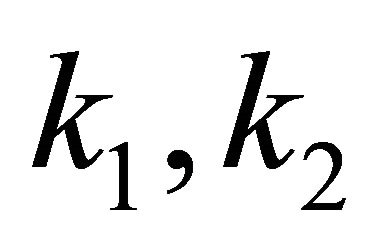such that

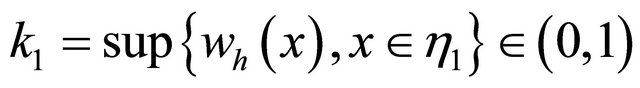
and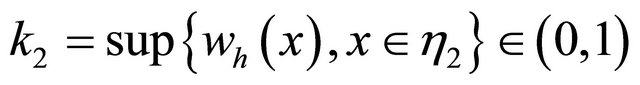

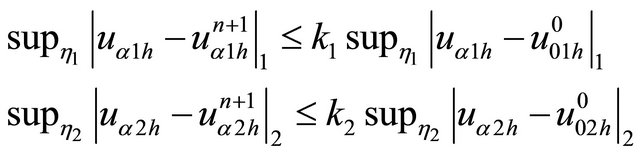(25)

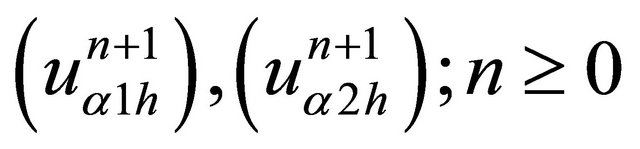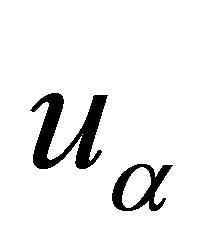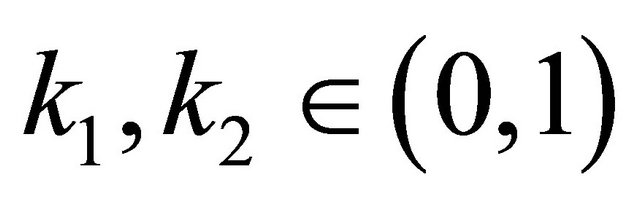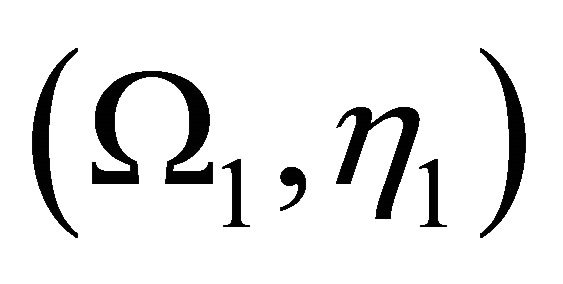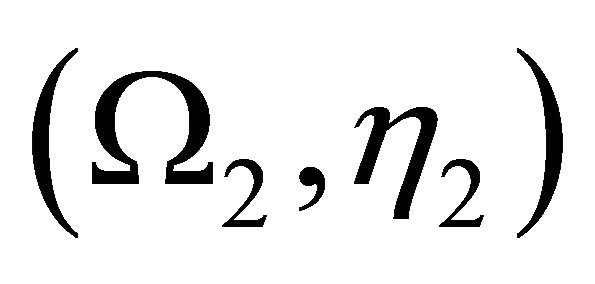Theorem 4 [8]: produced by Schwarz alternating method converges geometrically to the solution of obstacle problem, more precisely, there exist which depend only respectively of and, such that

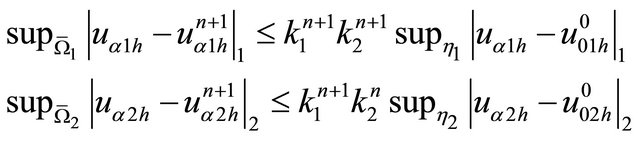(26)

Theorem 5: Let 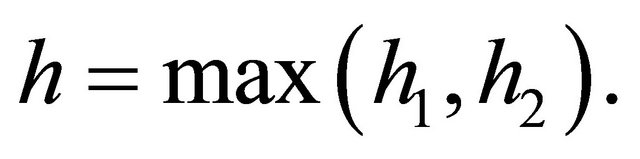Then, there exist two constants C and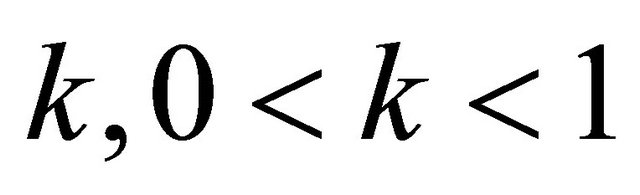, independent of both h and n such that:

and

.

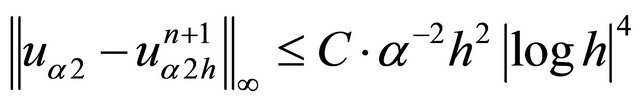Proof:

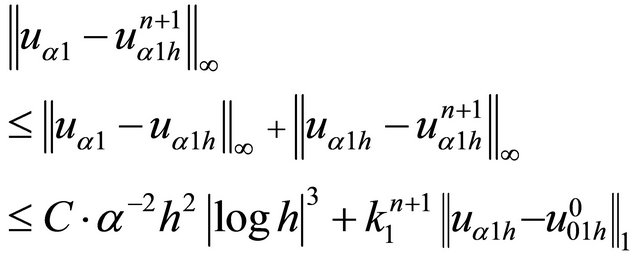
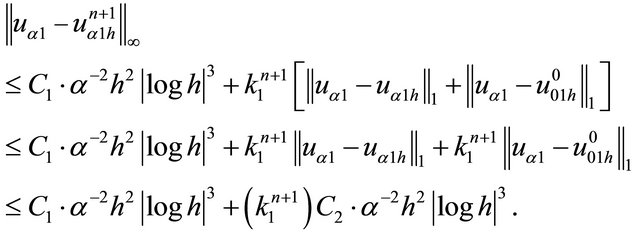
We obtain

.

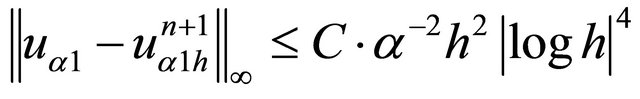The case i = 2 is similar.

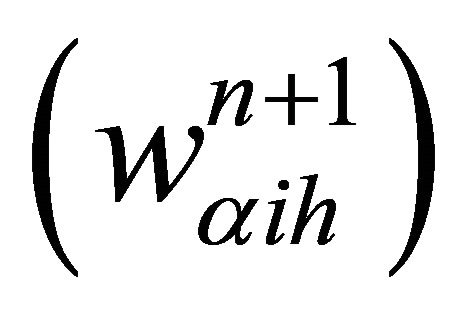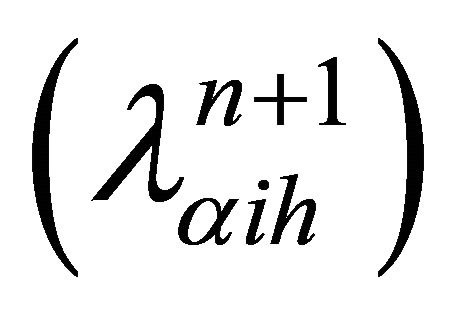Theorem 6: Let and, the discretes alternating Schwarz sequences, we have:

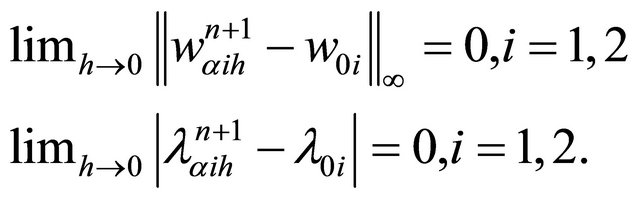
Proof:

1)

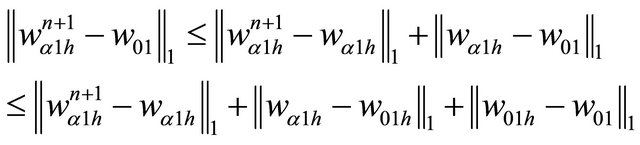
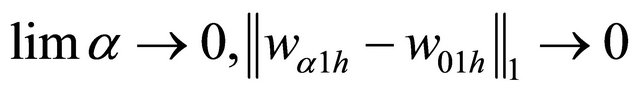
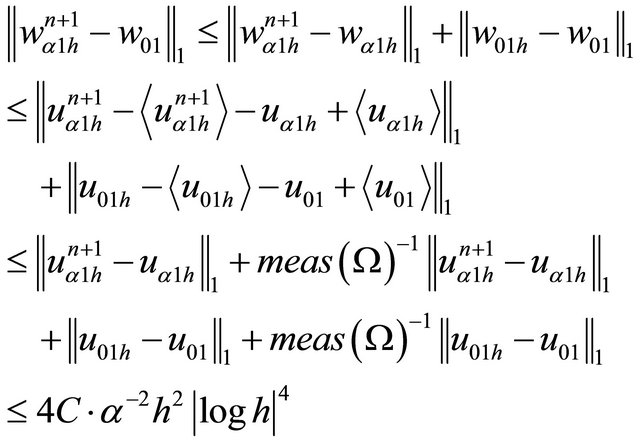
For: 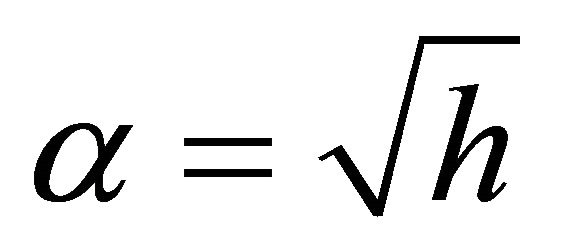and.

The case i = 2 is similar.

.

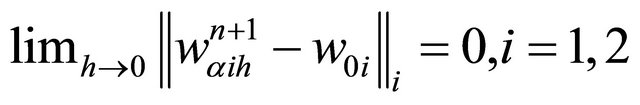2)

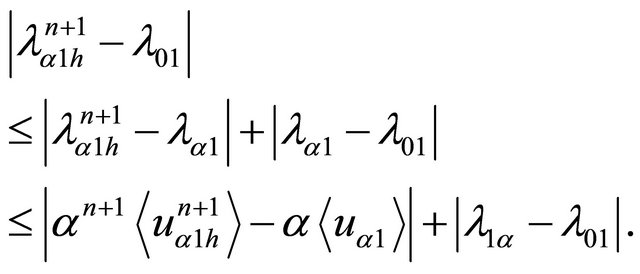
Hence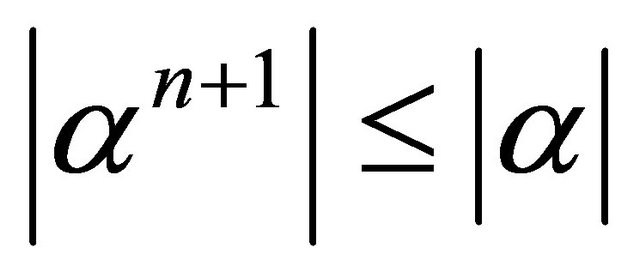: for

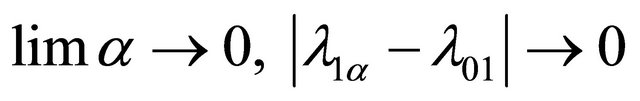, For: 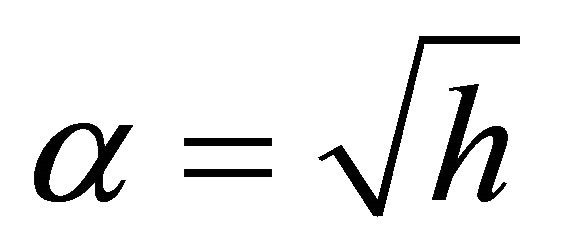and.

The case i = 2 is similar.

.

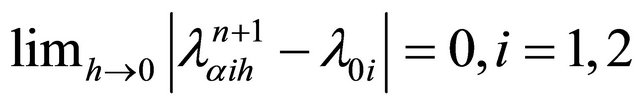REFERENCES