American Journal of Computational Mathematics
Vol.2 No.1(2012), Article ID:17962,9 pages DOI:10.4236/ajcm.2012.21005
Heat Generation Effects on MHD Natural Convection Flow along a Vertical Wavy Surface with Variable Thermal Conductivity
1Department of Mathematics, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh
2Department of Mathematics, Jagannath University, Dhaka, Bangladesh
3Department of Mathematics, Dhaka Commerce College, Dhaka, Bangladesh
Email: {a0alim, mirajaknd}@gmail.com, rrezaul@yahoo.com
Received December 30, 2011; revised January 20, 2012; accepted January 30, 2012
Keywords: Natural Convection; Magnetohydrodynamics; Heat Transfer; Wavy Surface; Temperature Dependent Thermal Conductivity; Heat Generation
ABSTRACT
The heat generation effects on magnetohydrodynamic(MHD) natural convection flow along a vertical wavy surface with variable thermal conductivity have been investigated. The governing boundary layer equations are first transformed into a non-dimensional form using suitable set of dimensionless variables. The resulting nonlinear system of partial differential equations are mapped into the domain of a vertical flat plate and then solved numerically employing the implicit finite difference method, known as Keller-box scheme. The numerical results of the surface shear stress in terms of skin friction coefficient and the rate of heat transfer in terms of local Nusselt number, the stream lines as well as the isotherms are shown graphically for a selection of parameters set consisting of thermal conductivity variation parameter, heat generation parameter Q, magnetic parameter M and Prandtl number Pr. Comparison of numerical results of present work with other published data has been shown in table.
1. Introduction
The effects of heat generation on magnetohydrodynamic (MHD) free convection boundary layer on various geometrical shapes such as vertical flat plate, cylinder, sphere, vertical wavy surface etc, have been studied by many investigators and it has been a very popular research topic for many years. The natural convection heat transfer from an isothermal vertical wavy surface was first studied by Yao [1] and using an extended Prantdl’s transposition theorem and a finite-difference scheme. He proposed a simple transformation to study the natural convection heat transfer from isothermal vertical wavy surfaces, such as sinusoidal surface. Moulic and Yao [2] also investigated mixed convection heat transfer along a vertical wavy surface. Alam et al. [3] have also studied the problem of free convection from a wavy vertical surface in presence of a transverse magnetic field. Combined effects of thermal and mass diffusion on the natural convection flow of a viscous incompressible fluid along a vertical wavy surface have been investigated by Hossain and Rees [4]. Wang and Chen [5] investigated transient force and free convection along a vertical wavy surface in micropolar fluid. Kabir et al. [6] have studied the problem of natural convection of fluid with temperature dependent viscosity along a heated vertical wavy surface. Natural and mixed convection heat and mass transfer along a vertical wavy surface have been investigated by Jang et al. [7] and Jang and Yan [8]. Molla et al. [9] have studied natural convection flow along a vertical wavy surface with uniform surface temperature in presence of heat generation/absorption. Tashtoush and Al-Odat [10] investigated magnetic field effect on heat and fluid flow over a wavy surface with a variable heat flux. Yao [11] studied natural convection along a vertical complex wavy surface. Very recently, Miraj et al. [12] studied conjugate effects of radiation and joule heating on magnetohydrodynamic free convection flow along a sphere with heat generation. Patel and Timol [13] studied magnetohydrodynamic orthogonal stagnation point flow of a power-law fluid toward a stretching surface. Parveen and Alim [14] investigated Joule heating effect on magnetohydrodynamic natural convection flow along a vertical wavy surface with viscosity dependent on temperature. The thermal conductivity of the fluid had been assumed to be constant in all the above studies. However, it is known that this physical property may be change significantly with temperature. For a liquid, it has been found that the thermal conductivity varies with temperature in an approximately linear manner in the range from 0 to 4000 F by Kays [15]. Hossain et al. [16] investigated the natural convection flow past a permeable wedge for the fluid having temperature dependent viscosity and thermal conductivity. The governing partial differential equations are reduced to locally non-similar partial differential forms by adopting some appropriate transformations. The transformed boundary layer equations are solved numerically using implicit finite difference scheme together with Keller box technique [17] and later by Cebeci and Bradshaw [18] along with Newton’s linearization approximation. Numerical results have been obtained in terms of local skin friction, rate of heat transfer for a selection of relevant physical parameters are shown graphically.
2. Formulation of the Problem
It is assumed that the surface temperature of the vertical wavy surface Tw is uniform, where Tw > T¥. The boundary layer analysis outlined below allows 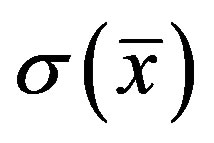 being arbitrary, but our detailed numerical work assumed that the surface exhibits sinusoidal deformations. The wavy surface may be described by
being arbitrary, but our detailed numerical work assumed that the surface exhibits sinusoidal deformations. The wavy surface may be described by
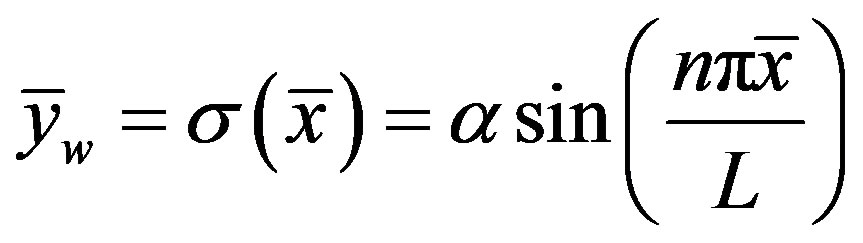 (1)
(1)
where L is the characteristic length associated with the wavy surface.
The geometry of the wavy surface and the two-dimensional coordinate system are shown in Figure 1.
The conservation equations for the flow characterized with steady, laminar and two-dimensional boundary layer; under the usual Boussinesq approximation, the continuity, momentum and energy equations can be written as:

Figure 1. Physical model and coordinate system.
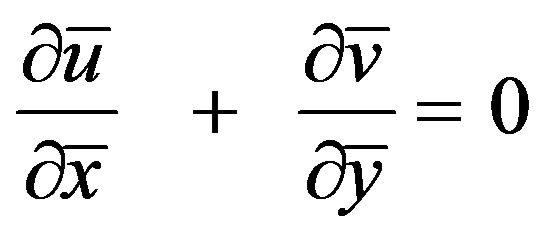 (2)
(2)
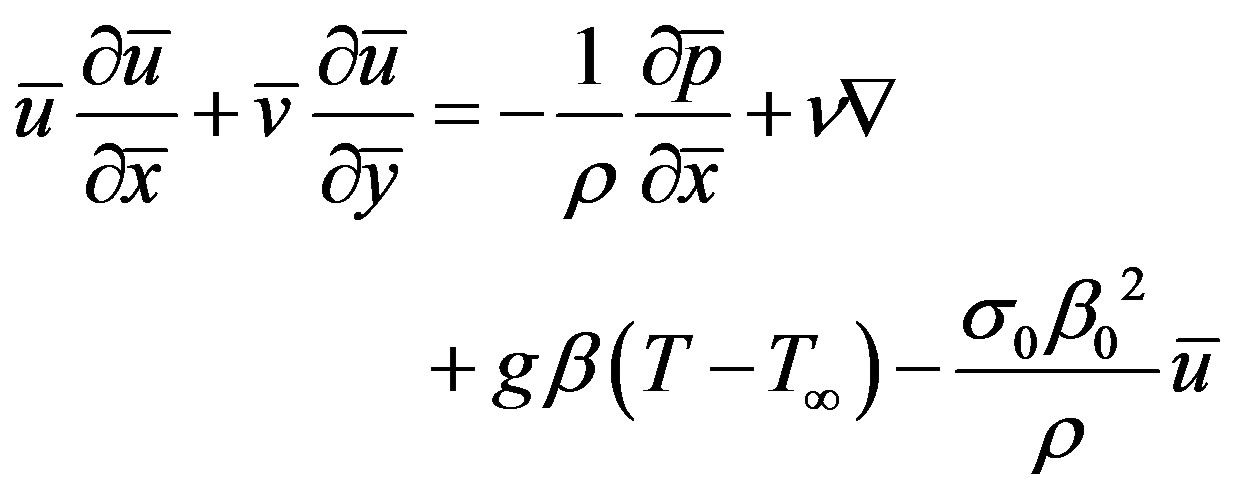 (3)
(3)
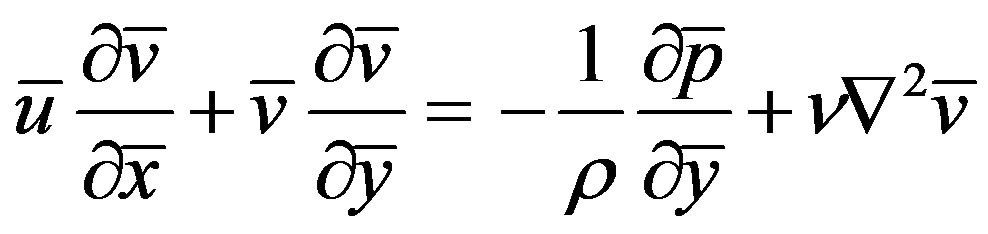 (4)
(4)
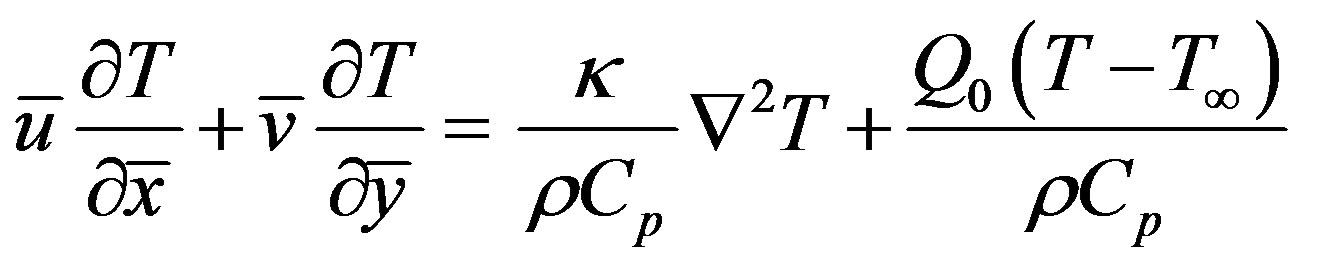 (5)
(5)
where 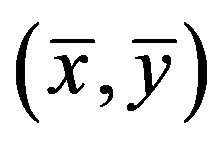 are the dimensional coordinates along and normal to the tangent of the surface and
are the dimensional coordinates along and normal to the tangent of the surface and  are the velocity components parallel to
are the velocity components parallel to ,
,  is the Laplacian operator, g is the acceleration due to gravity,
is the Laplacian operator, g is the acceleration due to gravity, 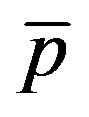 is the dimensional pressure of the fluid, r is the density, b0 is the strength of magnetic field, s0 is the electrical conduction, k is the thermal conductivity of the fluid in the boundary layer region depending on the fluid temperature, b is the coefficient of thermal expansion, n is the kinematics viscosity, m is the dynamic viscosity and Cp is the specific heat due to constant pressure.
is the dimensional pressure of the fluid, r is the density, b0 is the strength of magnetic field, s0 is the electrical conduction, k is the thermal conductivity of the fluid in the boundary layer region depending on the fluid temperature, b is the coefficient of thermal expansion, n is the kinematics viscosity, m is the dynamic viscosity and Cp is the specific heat due to constant pressure.
The boundary conditions relevant to the above problem are
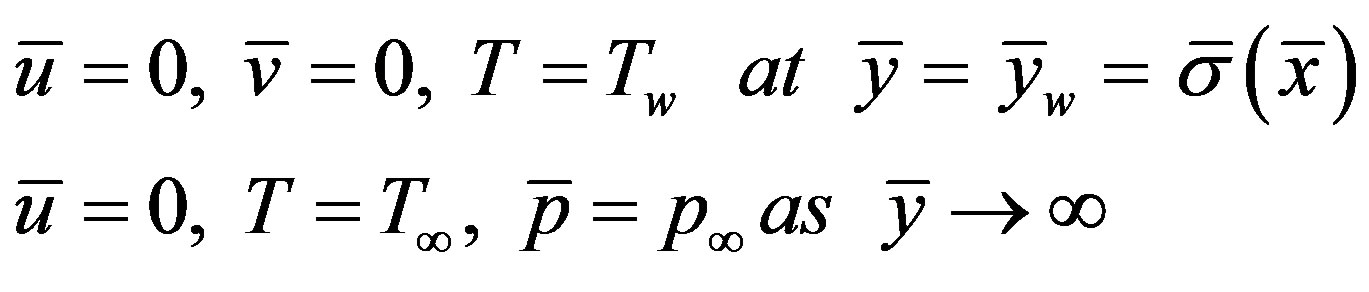 (6)
(6)
where Tw is the surface temperature, T¥ is the ambient temperature of the fluid and p¥ is the pressure of fluid outside the boundary layer.
There are very few forms of thermal conductivity variation available in the literature. Among them we have considered that one which is appropriate for liquid introduced by Hossain et al. [16] as follows:
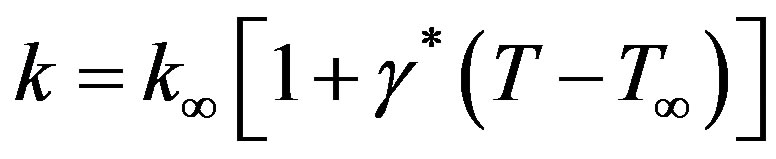 (7)
(7)
where k¥ is the thermal conductivity of the ambient fluid and  is a constant evaluated at the film temperature of the flow
is a constant evaluated at the film temperature of the flow .
.
Using Prandtl’s transposition theorem to transform the irregular wavy surface into a flat surface as extended by Yao [1] and boundary-layer approximation, the following dimensionless variables were introduced for non-dimensionalizing the governing equations:
 ,
, 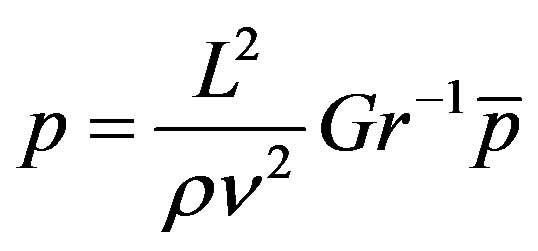
 (8)
(8)
 ,
, 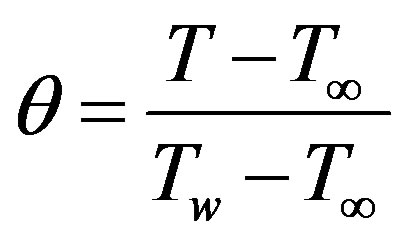
where q is the non-dimensional temperature function and (u, v) are the dimensionless velocity components parallel to (x, y). Introducing the above dimensionless dependent and independent variables into Equations (2)-(5), the following dimensionless form of the governing equations are obtained after ignoring terms of smaller orders of magnitude in Gr, the Grashof number defined in (8).
 (9)
(9)
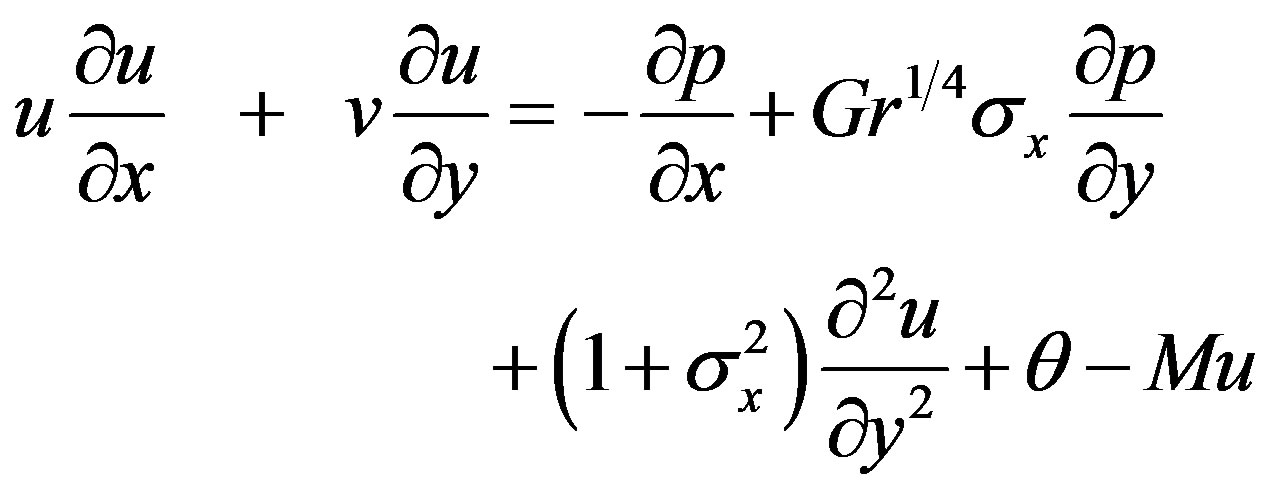 (10)
(10)
 (11)
(11)
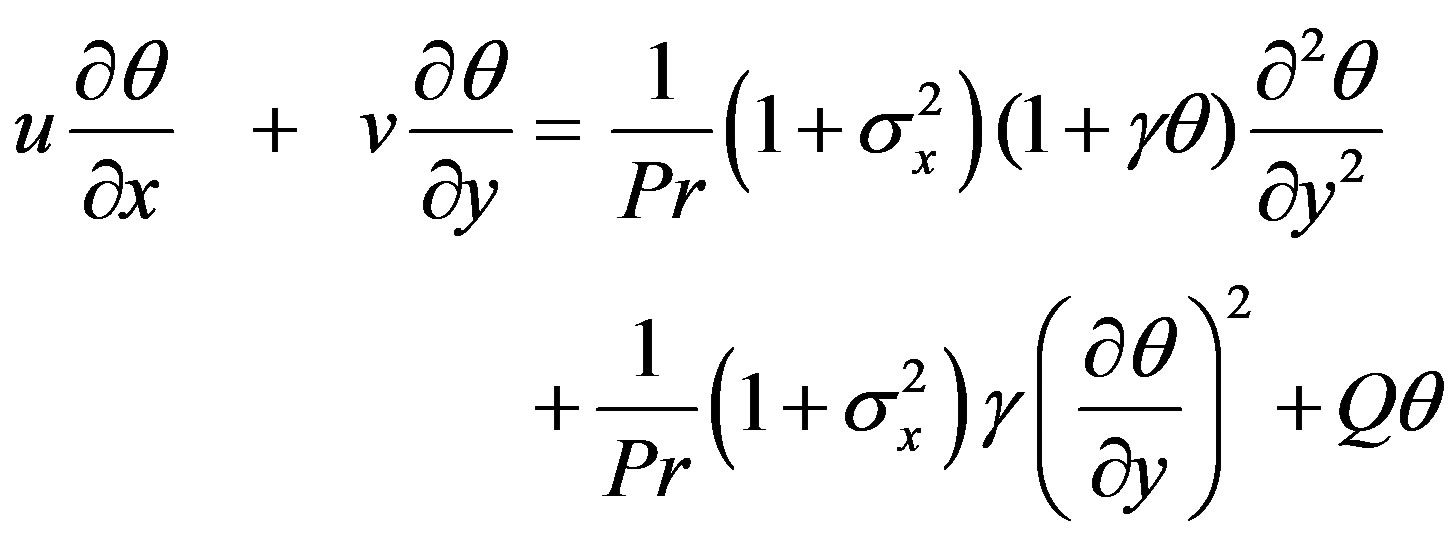 (12)
(12)
where 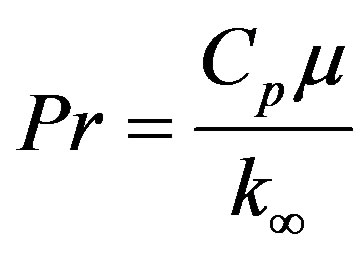 is the Prandtl number,
is the Prandtl number, 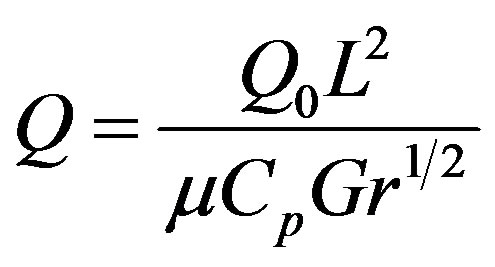
is the heat generation parameter, 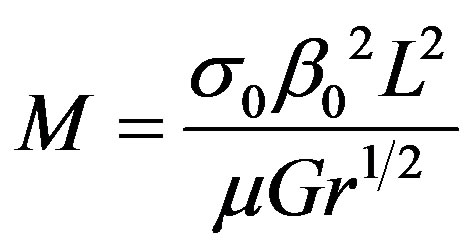 is the magnetic parameter and
is the magnetic parameter and  is the thermal conductivity variation parameter.
is the thermal conductivity variation parameter.
It can easily be seen that the convection induced by the wavy surface is described by Equations (9)-(12). Equation (11) indicates that the pressure gradient along the y-direction, which implies that lowest order pressure gradient along x -direction can be determined from the inviscid flow solution. For the present problem this pressure gradient (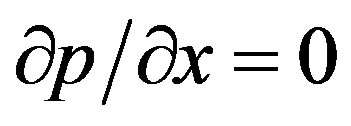 ) is zero. The elimination of
) is zero. The elimination of 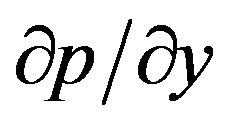 from Equations (10) and (11) leads to the following equation:
from Equations (10) and (11) leads to the following equation:
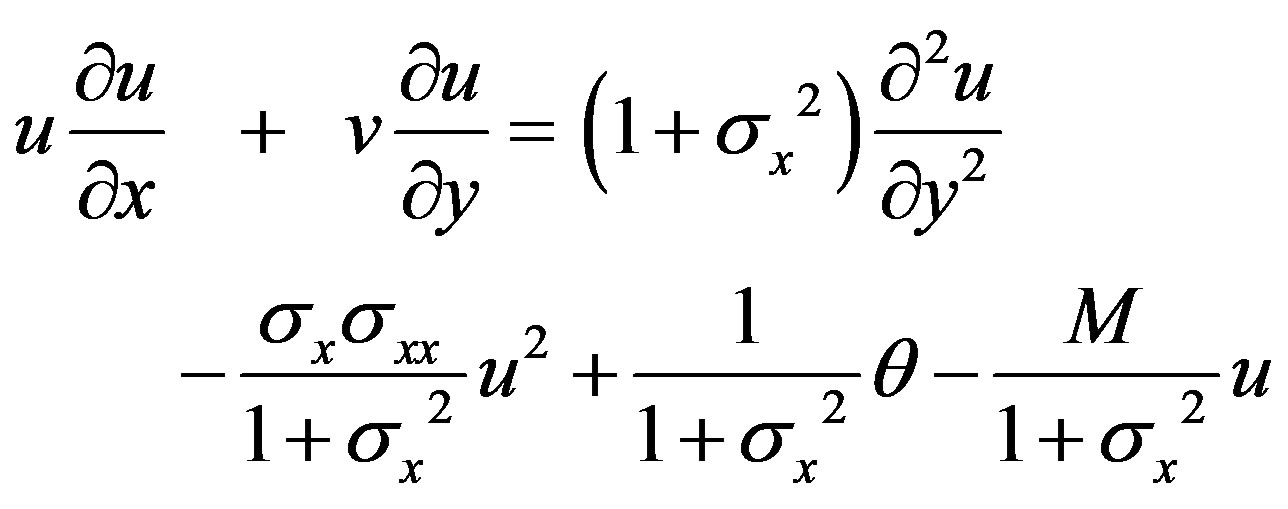 (13)
(13)
The corresponding boundary conditions for the present problem then turn into
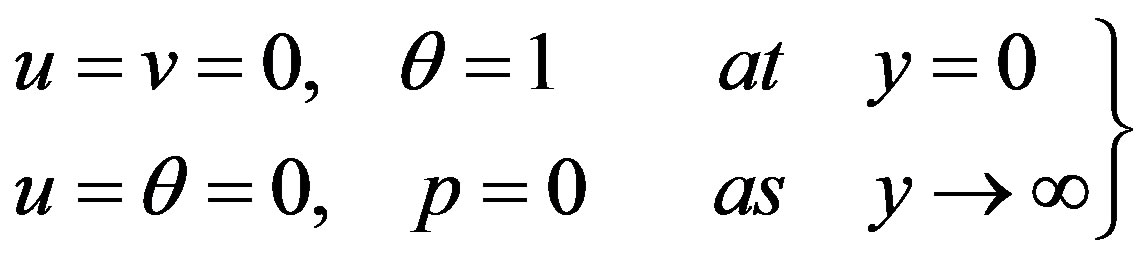 (14)
(14)
Now we introduce the following transformations to reduce the governing equations to a convenient form:
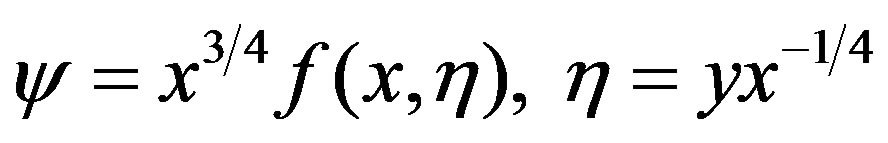 and
and 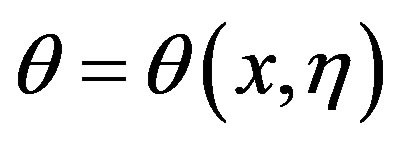 (15)
(15)
where f(η) is the dimensionless stream function, η is the pseudo similarity variable and ψ is the stream function that satisfies the Equation (9) and is defined by
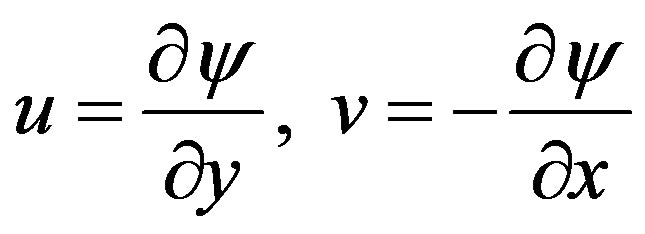 (16)
(16)
Using the above transformed values in Equations (12) and (13) and by simplified, we have the following equation:
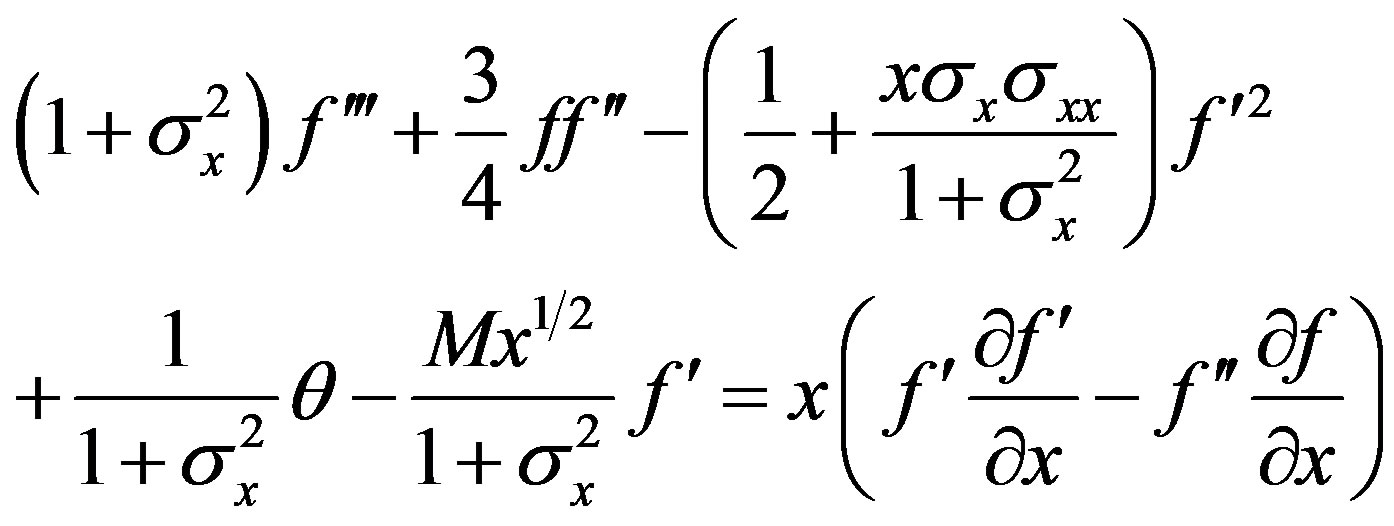 (17)
(17)
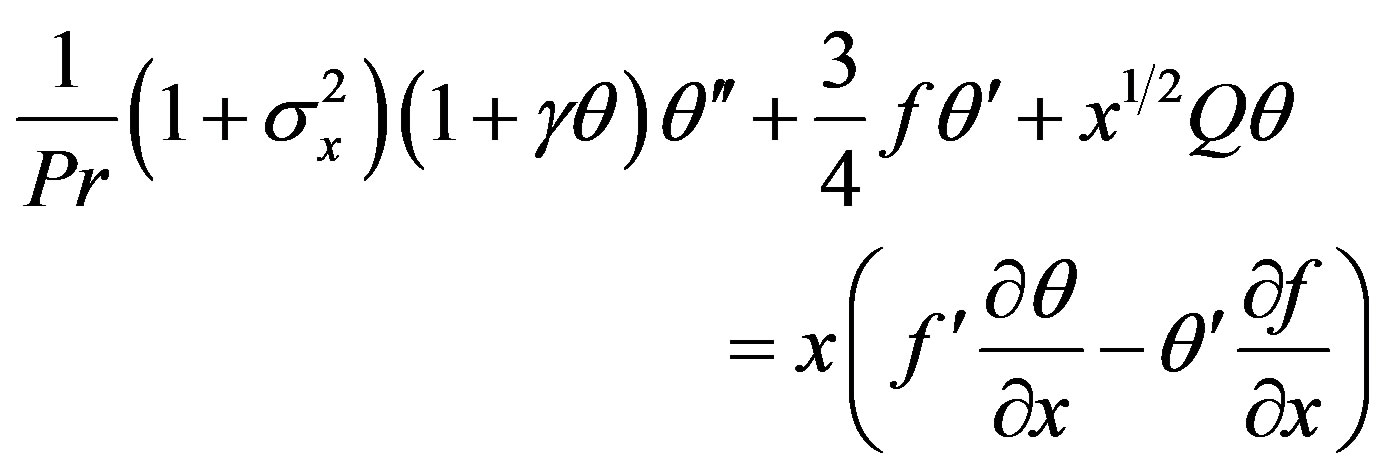 (18)
(18)
The boundary conditions (14) now take the following form:
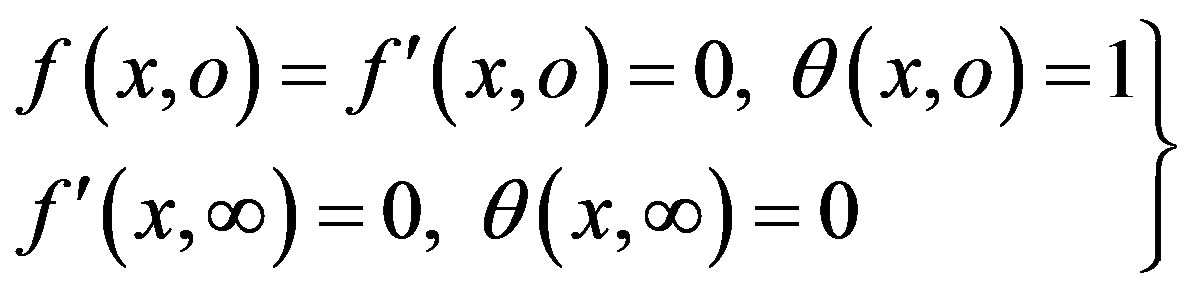 (19)
(19)
In the above equations prime denote the differentiation with respect to η.
Solutions of the local non-similar partial differential Equations (17) and (18) together with the boundary condition (19) are solved numerically by using implicit finite difference method with Keller-box scheme.
In practical applications, the physical quantities of principle interest are the shearing stress tw in terms of the skin friction coefficients Cf and the rate of heat transfer in terms of Nusselt number Nu which can be written as:
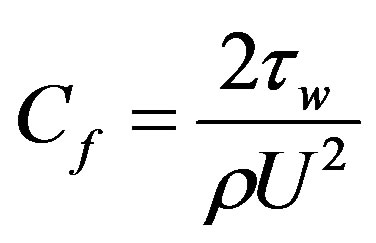 and
and 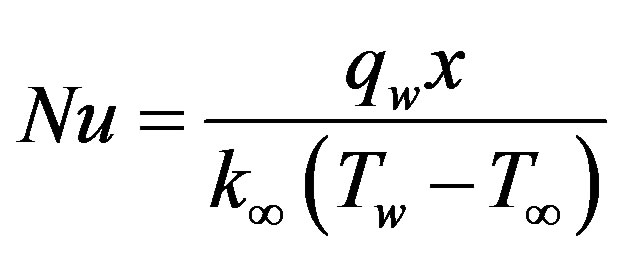 (20)
(20)
where 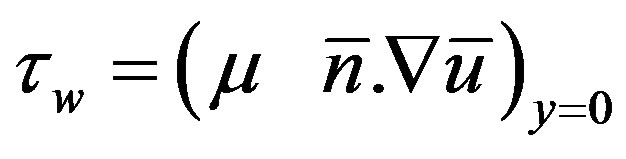 and
and  (21)
(21)
Using the transformations (15) into Equation (20), the local skin friction coefficient Cf and the rate of heat transfer in terms of the local Nusselt number Nu takes the following form:
 (22)
(22)
 (23)
(23)
Finally, it should be mentioned that for the computational purpose the period of oscillations in the waviness of this surface has been considered to be .
.
3. Results and Discussion
The objective of the present work is to analyze the effect of temperature dependent thermal conductivity on magnetohydrodynamic(MHD) free convection flow along a vertical wavy surface with heat generation. Although there are three parameters of interest namely, amplitude of the wavy surface a, thermal conductivity variation parameter g, heat generation parameter Q, magnetic parameter M and Prandtl number Pr. Numerical values of local shearing stress and the rate of heat transfer are calculated from Equations (22) and (23) in terms of the skin friction coefficient Cf and Nusselt number Nu respectively for a wide range of the axial distance x starting from the leading edge for different values of the relevant parameters. The effects of thermal conductivity variation parameter g, heat generation parameter Q, magnetic parameter M and Prandtl number Pr on streamlines, isotherms, skin friction coefficient and the rate of heat transfer have been presented graphically in Figures 2-8.
The effects of thermal conductivity variation parameter g and heat generation parameter Q on the development of streamlines which are displayed in Figures 2(a)-(d) for the amplitude of the wavy surface a = 0.2, magnetic parameter M = 0.4 and Prandtl number Pr = 0.72. When Q = 0.0 and g = 0.0, the thermal conductivity is independent of temperature with Q = 0.0 as shown in Figure 2(a) and found that maximum value of stream function ψmax is 9.98. Figure 2(b) displays the results that an increasing values of g, the boundary layer thickness increases. In this case the maximum value of stream function ψmax is 10.12. For increasing values of heat generation parameter Q the boundary layer becomes thinner and the maximum value of stream function ψmax is 24.22 that is shown in Figure 2(c).The combined effects of g and Q are shown in Figure 2(d). Here the maximum value ψmax is 24.36. From these figures it is observed that the value of stream function ψ becomes higher for larger values of thermal conductivity variation parameter g and heat generation parameter Q as well. The variation of isotherms with thermal conductivity variation parameter g and the heat generation parameter Q for the amplitude of the wavy surface a = 0.2, magnetic parameter M = 0.4 and Prandtl number Pr = 0.72 are shown in Figures 3(a)-(d). We can say after observing the isotherms of these figures that temperature enhances within the boundary layer due to the higher values of g and heat generation parameter Q.
The variation of the local skin friction coefficient Cf and local rate of heat transfer Nu for different values of Prandtl number Pr with g = 0.0, a = 0.4, M = 0.4 and Q = 0.4 are shown in Figures 4(a) and (b). It is observed from these figures that for increasing values of the Prandtl number Pr the skin friction coefficient Cf decreases up to the certain position of x and from that position of x skin friction coefficient Cf cross the sides and then increases.

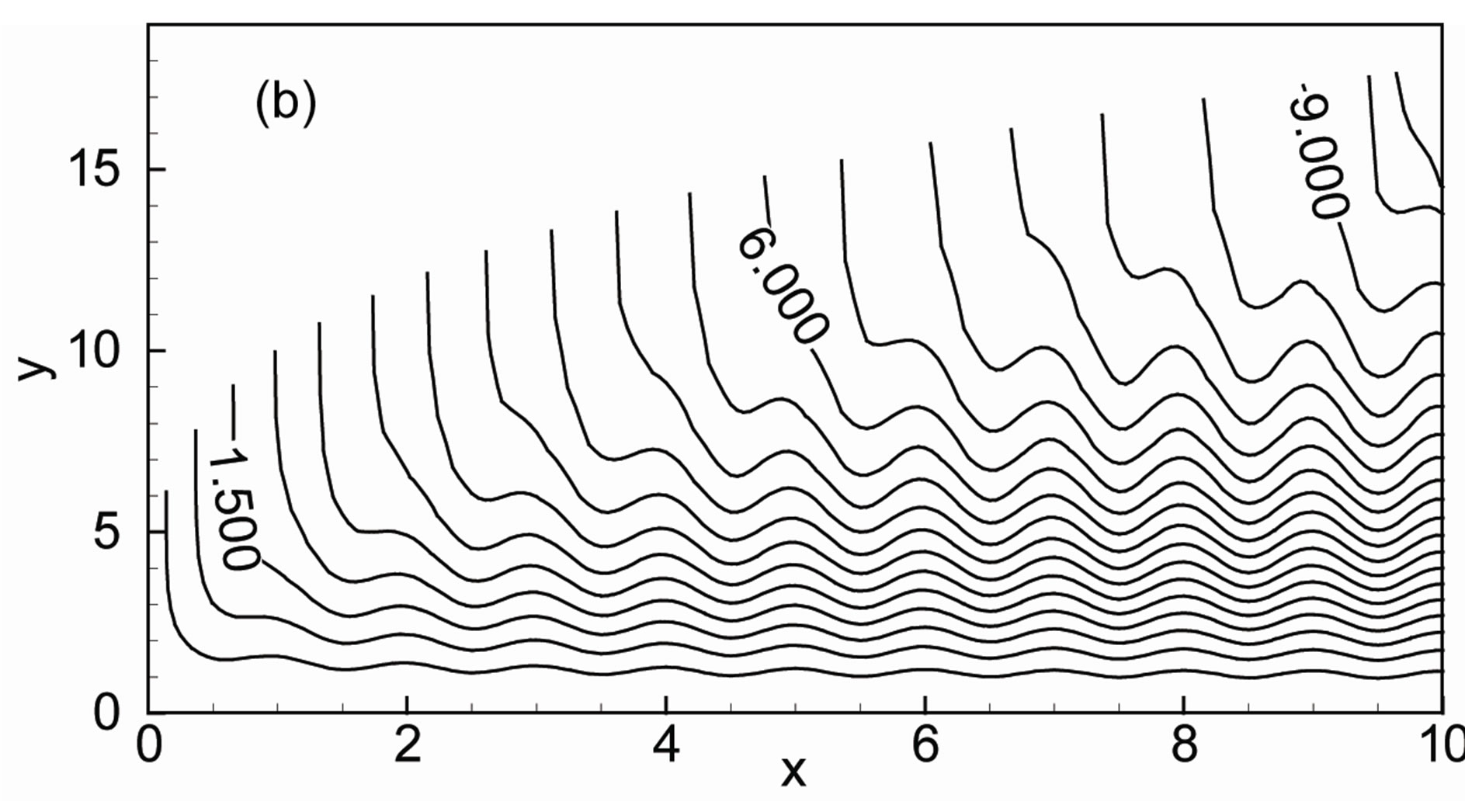

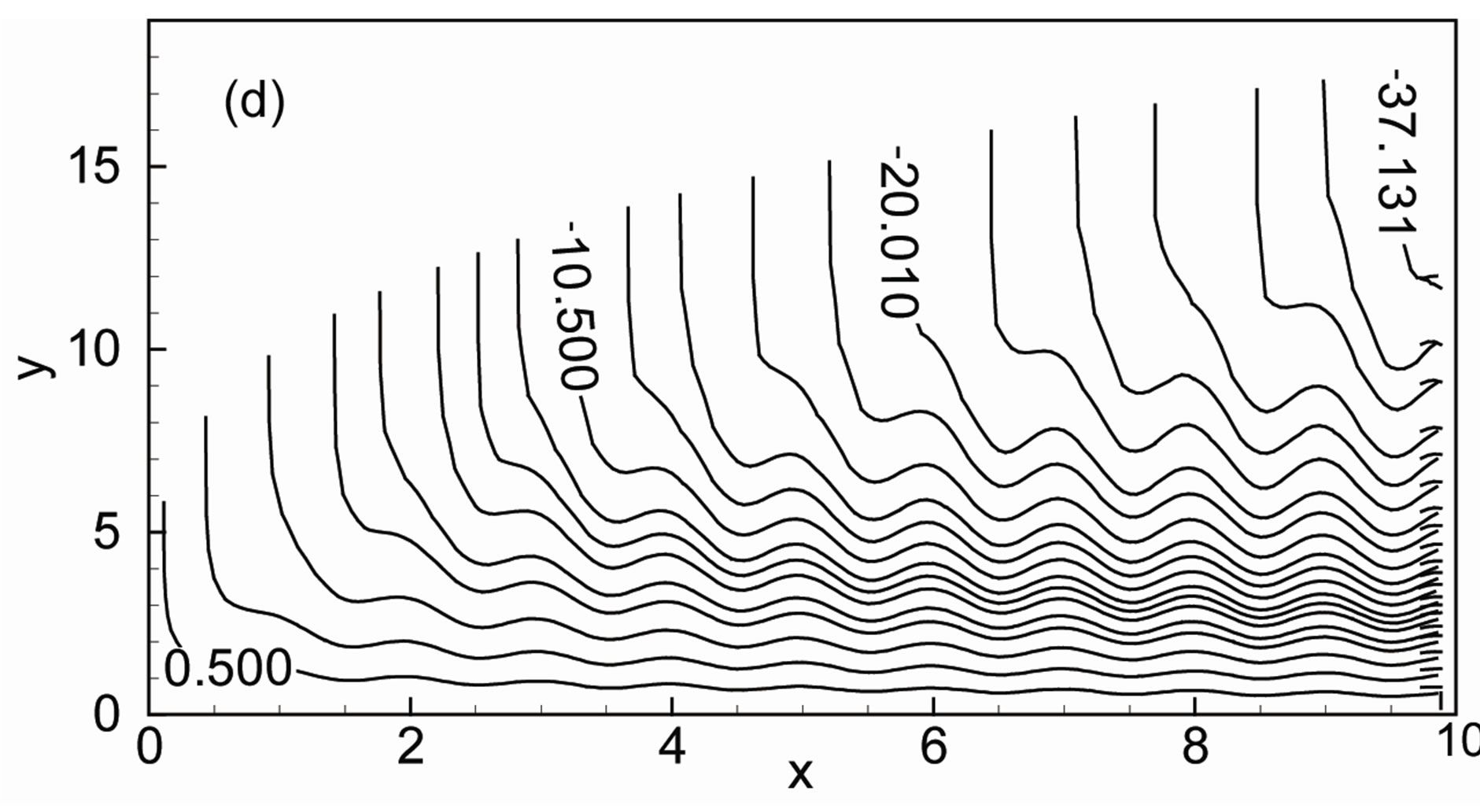
Figure 2. Streamlines for (a) Q = 0.0, g = 0.0; (b) Q = 0.0, g = 2.0; (c) Q = 1. 0, g = 0.0 and (d) Q = 1.0, g = 2.0 while Pr = 0.72, M = 0.4 and a = 0.2.
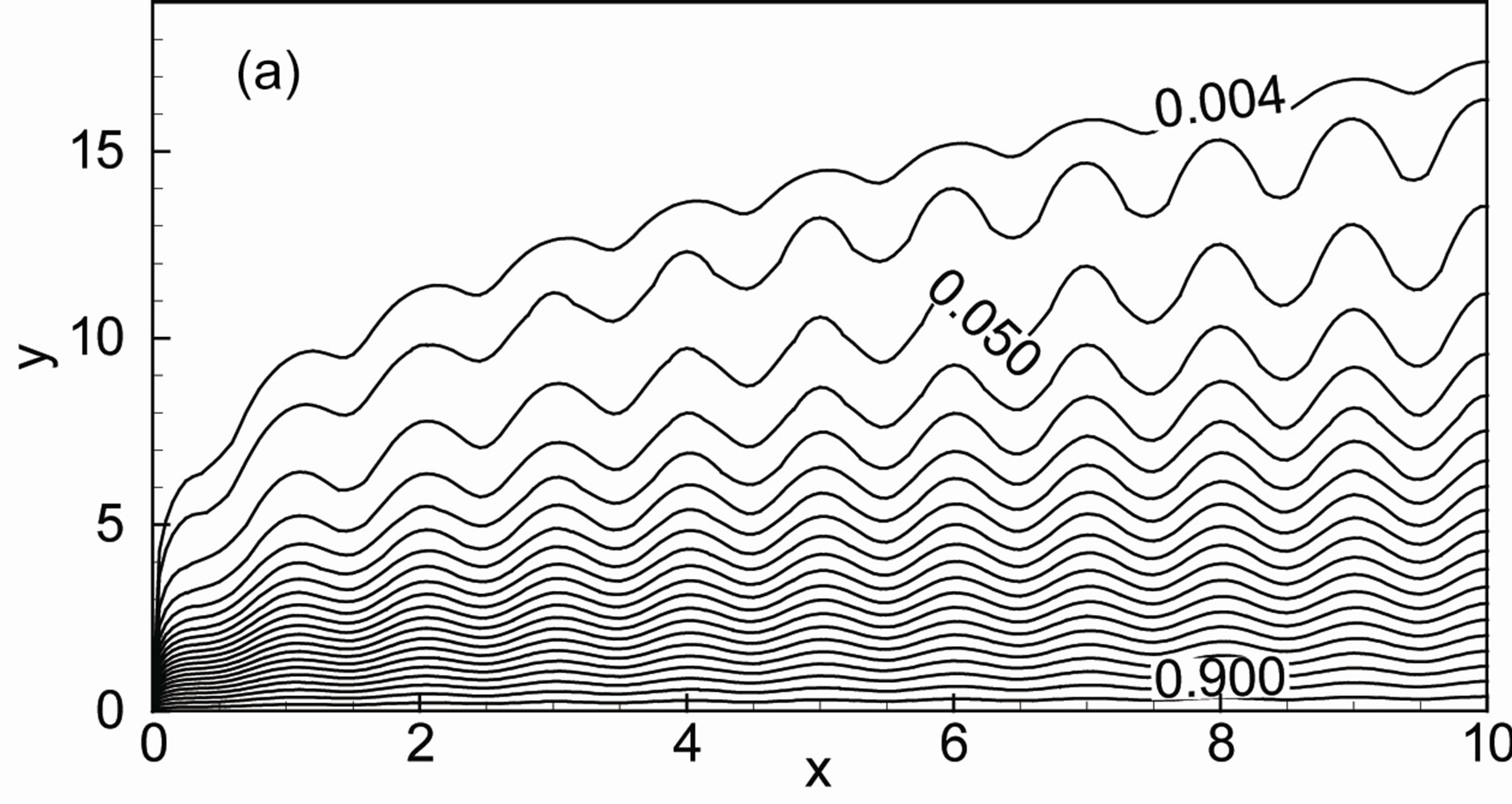

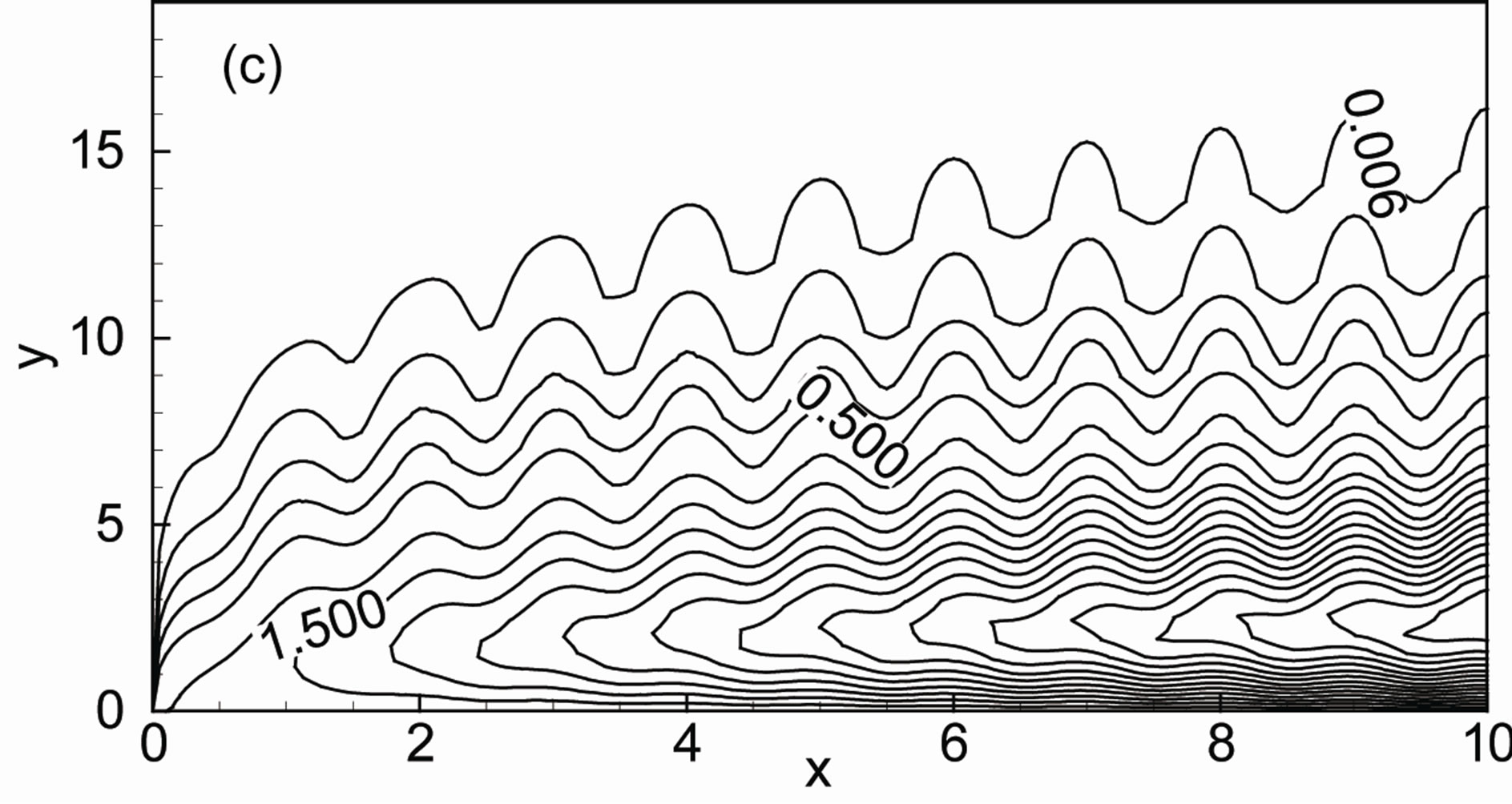
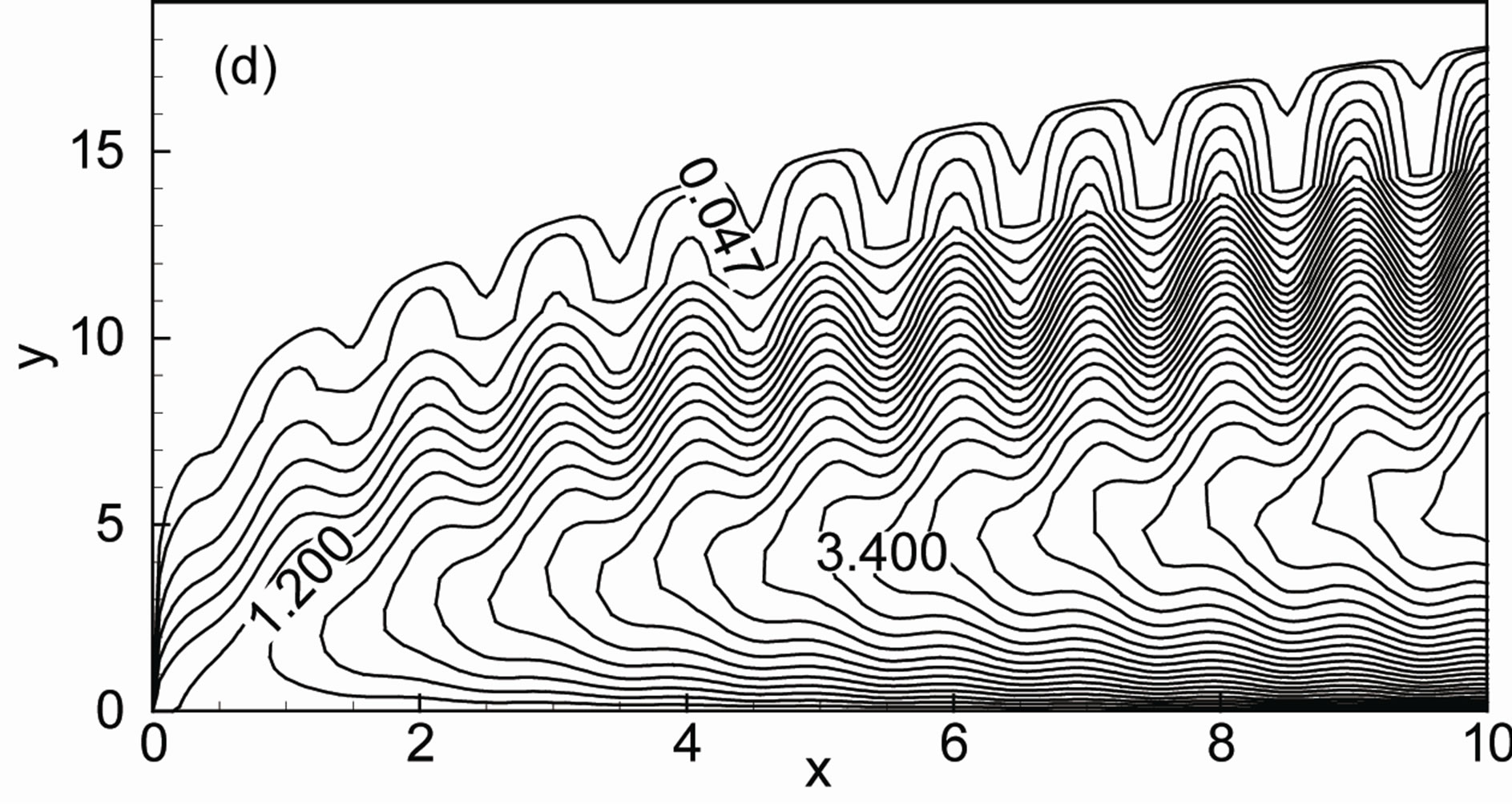
Figure 3. Isotherms for (a) Q = 0.0, g = 0.0; (b) Q = 0.0, g = 2.0; (c) Q = 1.0, g = 0.0 and (d) Q = 1.0, g = 2.0 while Pr = 0.72, M = 0.4 and a = 0.2.
The rate of heat transfer Nu decreases for increasing values of the Prandtl number Pr. The effects of g on skin friction coefficient Cf and the rate of heat transfer Nu while Q = 0.4, a = 0.4, M = 1.0 and Pr = 0.72 are shown in Figures 5(a) and (b). In Figure 5(a) it is shown that, as the parameter g increases the skin friction coefficient Cf increases up to the certain position of x and from that po-


Figure 4. Variation of (a) skin friction coefficient Cf and (b) rate of heat transfer Nu against x for different values of Prandtl number Pr with Q = 0.4, M = 1.0, g = 0.0 and a = 0.4.
sition of x skin friction coefficient Cf change with the increases of g. It is observed from this figure the skin friction coefficient Cf cross the sides and then the skin friction coefficient Cf decreases. It has been seen from Figure 5(b) that as g increases, the rate of heat transfer Nu increases up to the certain position of x and from that position of x rate of heat transfer Nux decreases. Since higher rate of heat transfer having higher gradient and drops of quicker than lower rate of heat transfer so, they tends to meet at a point and changed its behaviour with the increasing g.
Figures 6(a) and (b) display the results on the skin friction coefficient Cf and the rate of heat transfer Nu for different values of heat generation parameter Q while g = 2.0, a = 0.2, M = 0.5 and Pr = 0.72. It is observed from these figures that the skin friction coefficient Cf increases s but the rate of heat transfer Nu decreases. Figures 7(a) and (b), show that increase in the value of amplitude of wavy surface α leads to decrease of the value of the skin
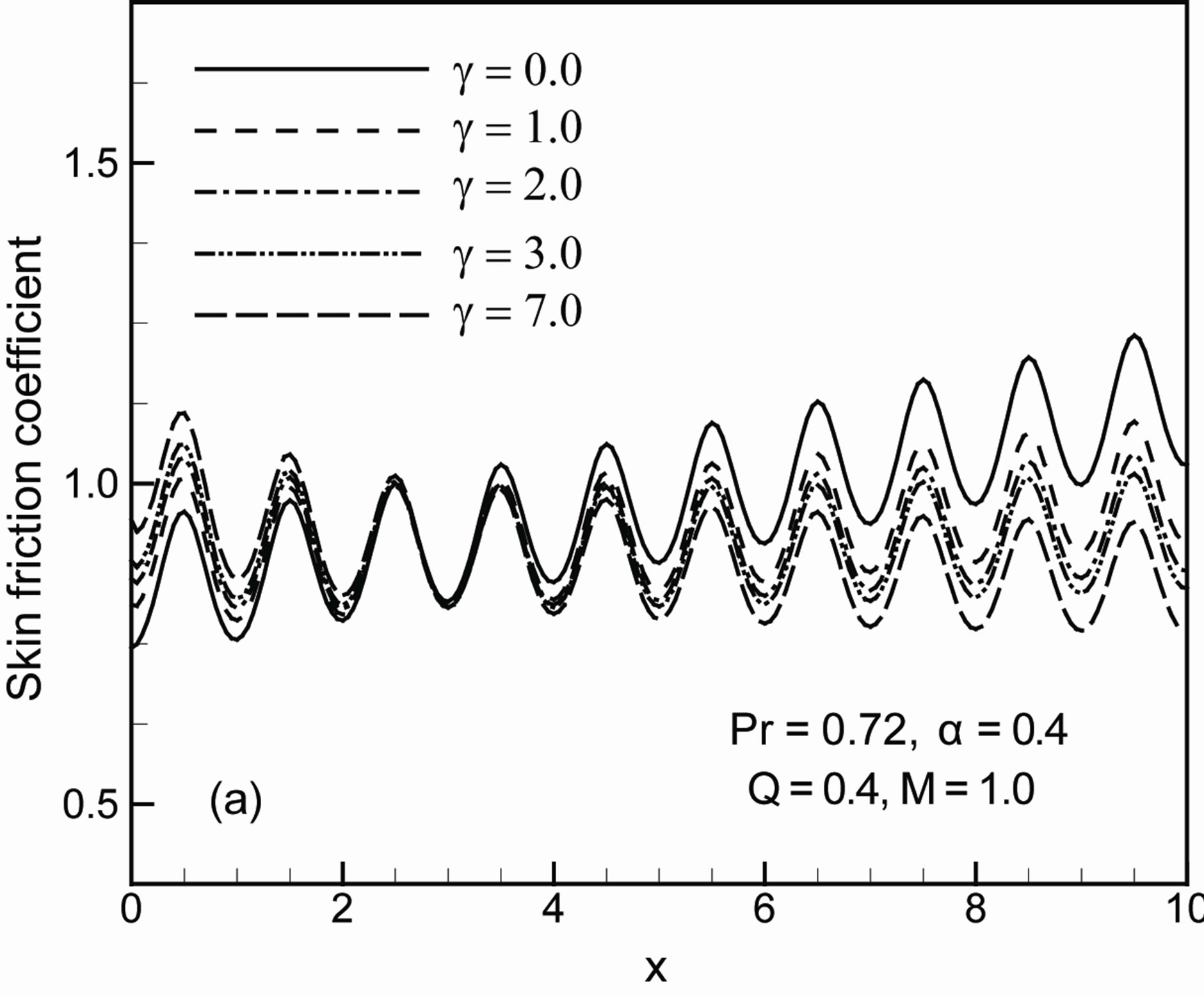
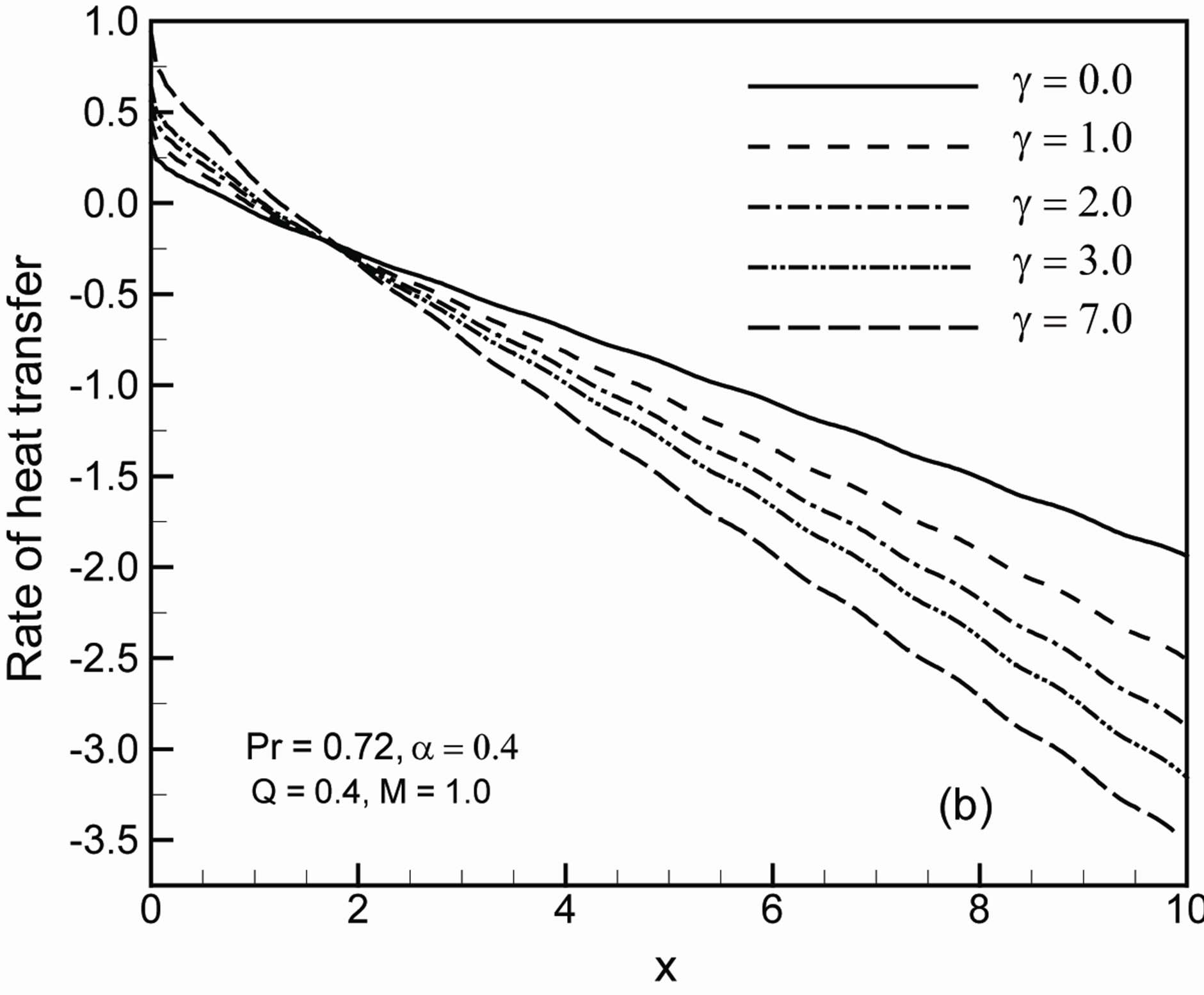
Figure 5. Variation of (a) skin friction coefficient Cf and (b) rate of heat transfer Nu against x for different values of thermal conductivity parameter g with Q = 0.4, a = 0.4, M = 1.0 and Pr = 0.72.
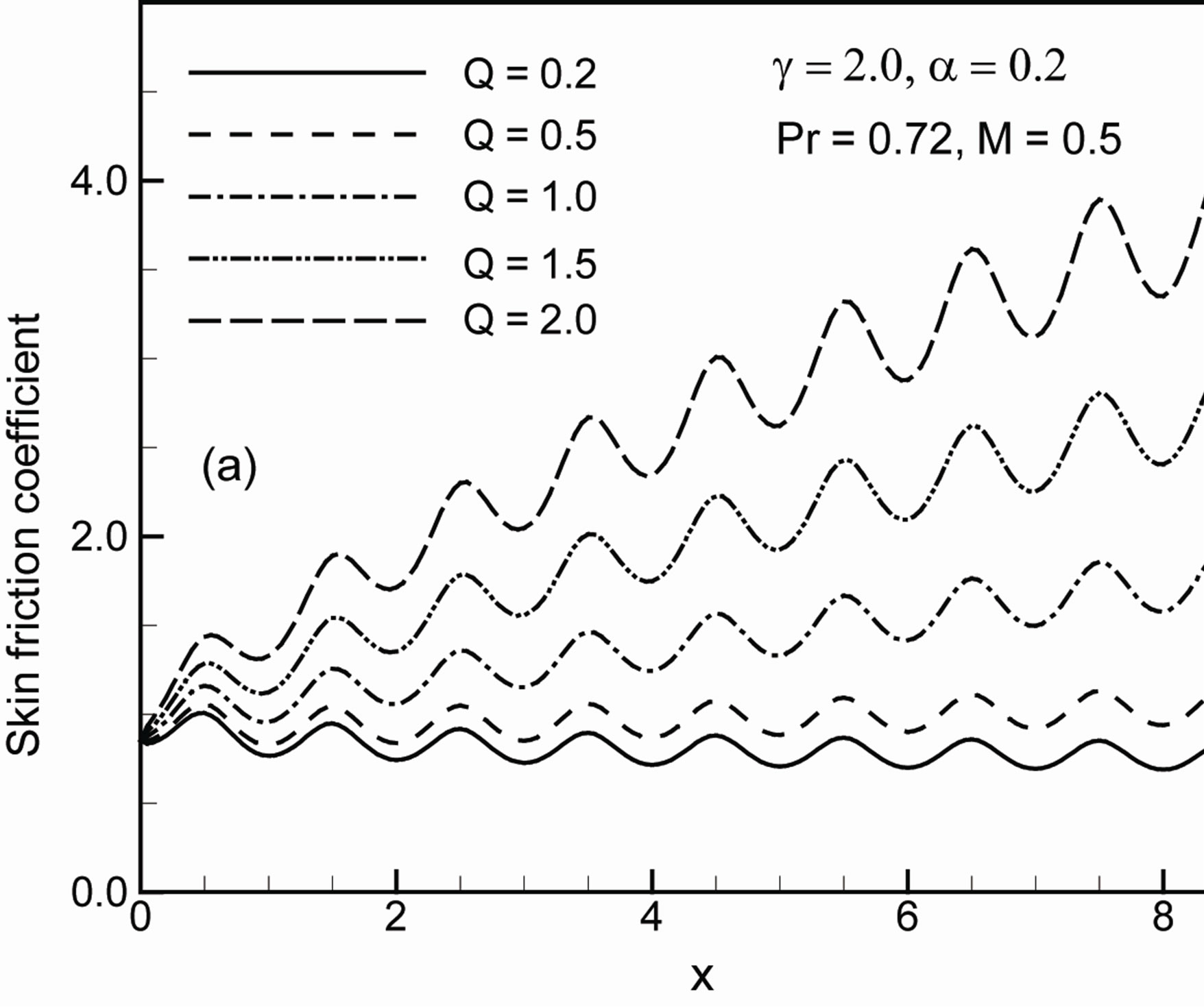
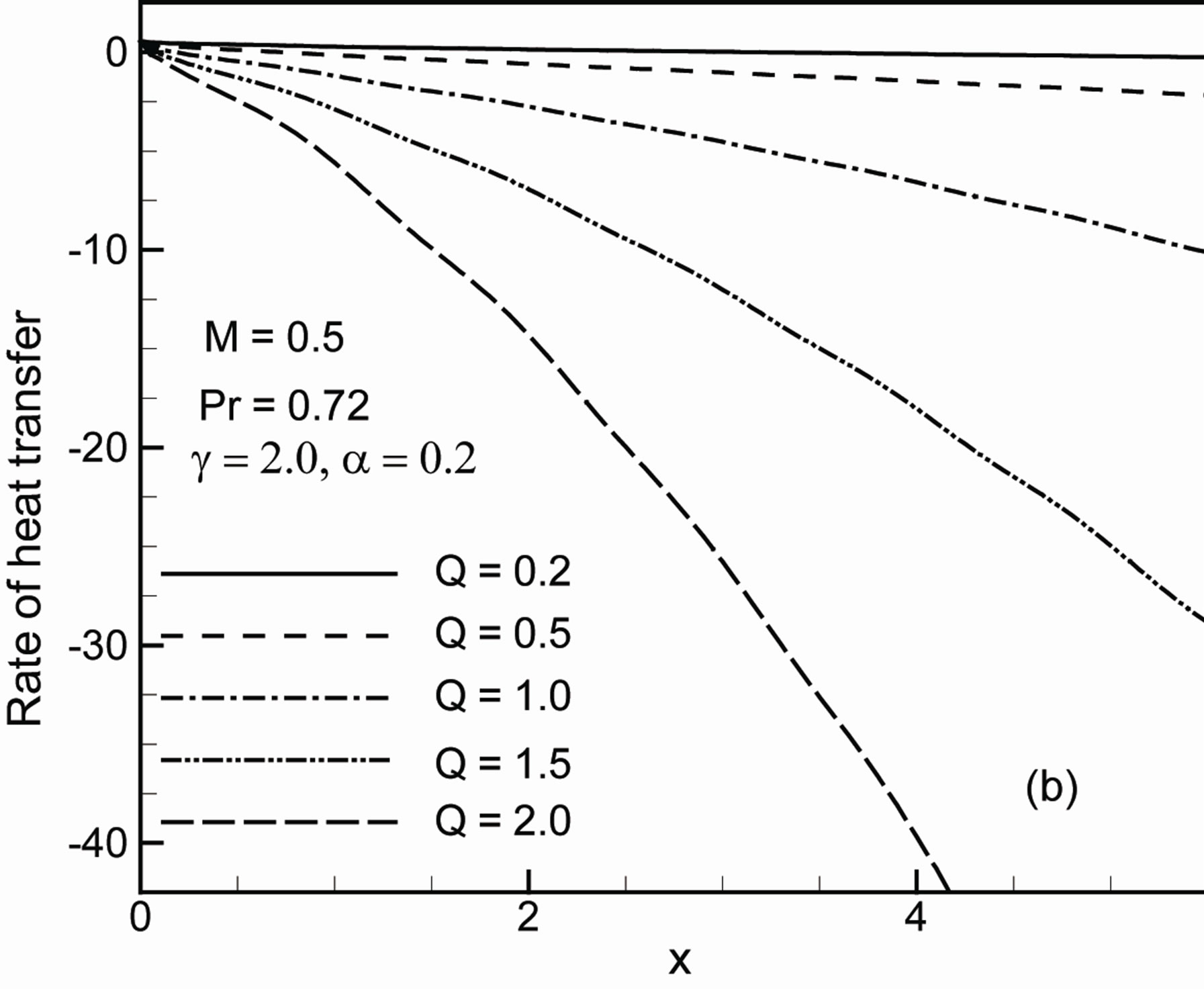
Figure 6. Variation of (a) skin friction coefficient Cf and (b) rate of heat transfer Nu against x for different values of heat generation parameter Q with g = 2.0, a = 0.2, M = 0.5 and Pr = 0.72.
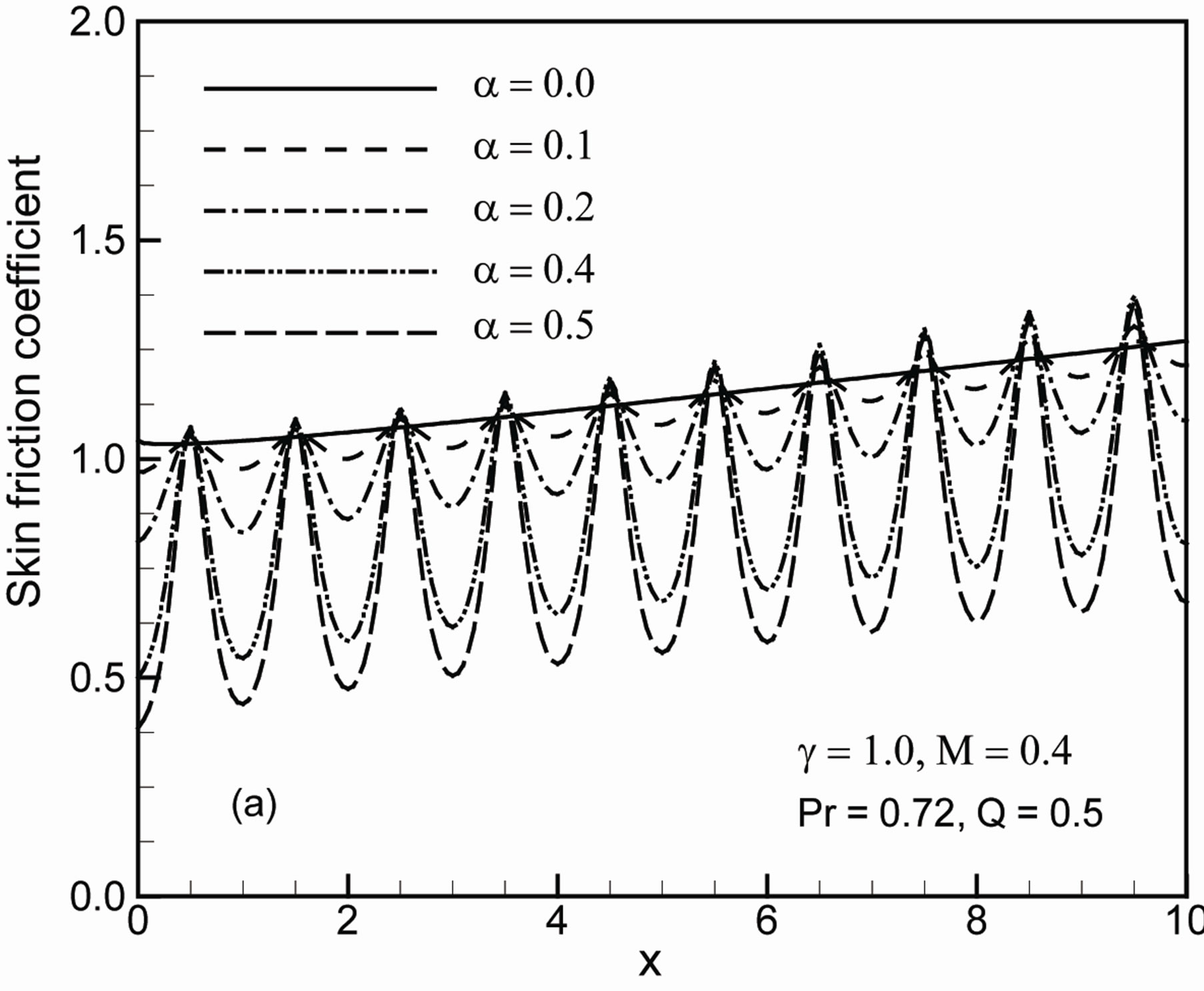
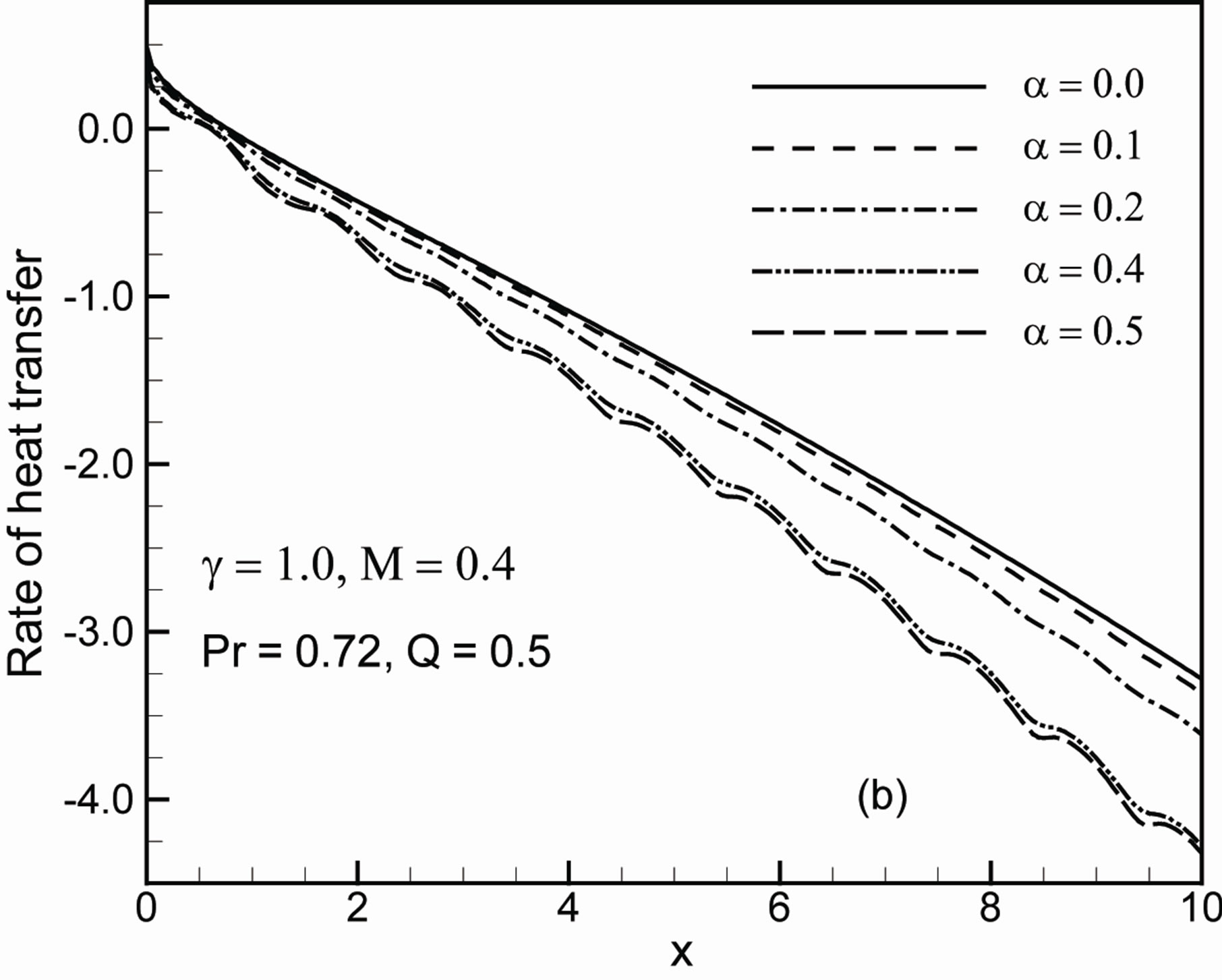
Figure 7. Variation of (a) skin friction coefficient Cf and (b) rate of heat transfer Nu against x for different values of a with g = 1.0, Q = 0.5, M = 0.4 and Pr = 0.72.
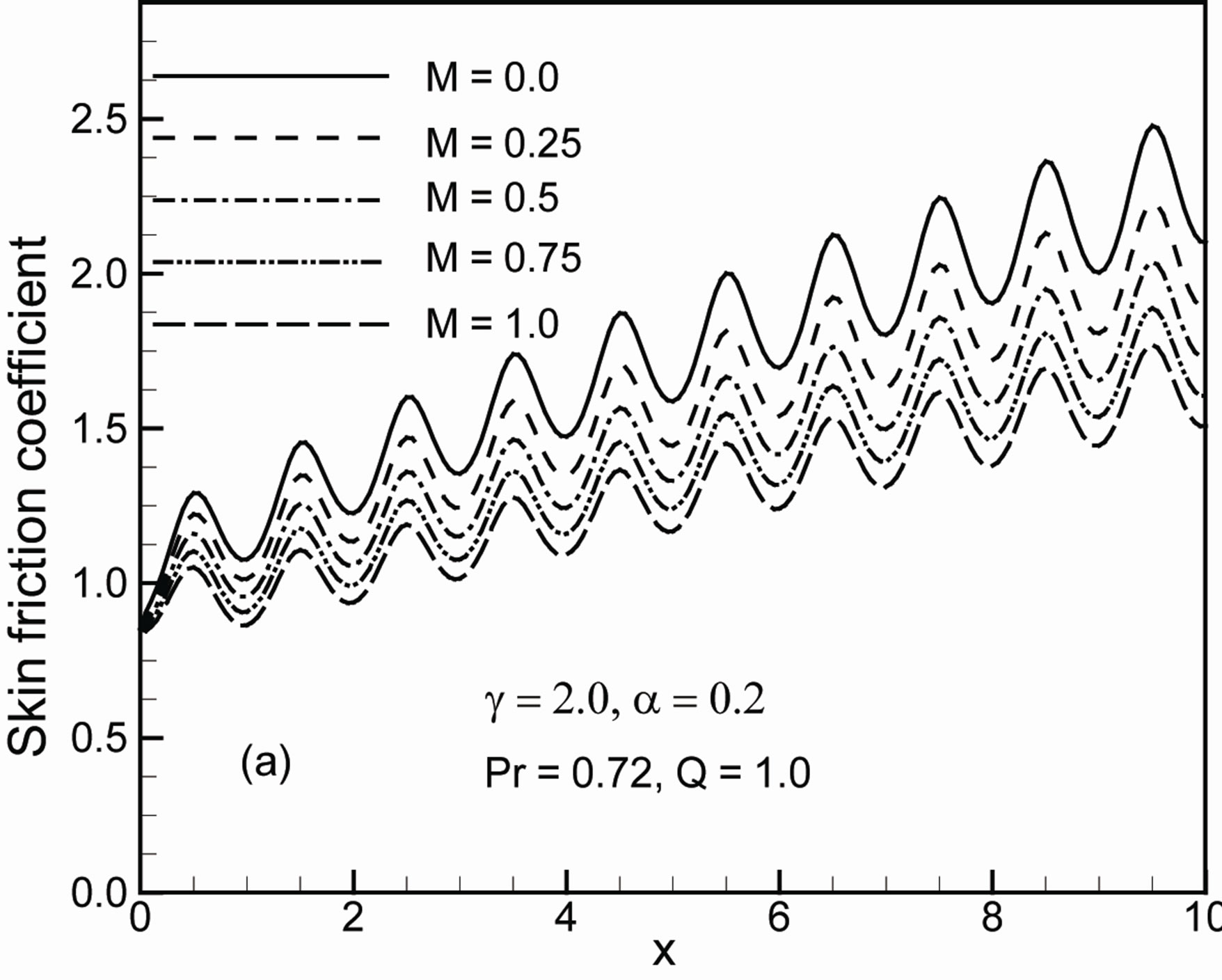

Figure 8. Variation of (a) skin friction coefficient Cf and (b) rate of heat transfer Nu against x for different values of magnetic parameter M with g = 2.0, a = 0.2, Q = 1.0 and Pr = 0.72.
friction coefficient and the rate of heat transfer in terms of the local Nusselt number Nu while g = 1.0, Q = 0.5, M = 0.4 and Pr = 0.72. The variation of the local skin friction coefficient Cf and local rate of heat transfer Nu for different values of M at different positions are illustrated in Figures 8(a)-(b) with g = 2.0, a = 0.2, Q = 1.0 and Pr = 0.72. From these figures it can be observed that an increase in the magnetic parameter M leads to decrease the local skin friction coefficient Cf and local rate of heat transfer Nu at different position of x. The skin friction coefficient and the rate of heat transfer coefficient decrease as M increases. The magnetic field acts against the flow and reduces the skin friction and the rate of heat transfer.
4. Comparison with Previous Work and Code Validation
A comparison of the present numerical results of the values of skin friction coefficient, f ²(x,0), and the heat transfer coefficient, –q'(x,0) with Hossain et al. [18] have been shown in Table 1. Here, the parameters Q and g are ignored to make the numerical data comparable with [19] for different values of Prandtl number Pr. It is evident from Table 1 that the present results agreed well with the results of Hossain et al. [19].
5. Conclusions
The effects of thermal conductivity variation parameter g, amplitude of the wavy surface a, magnetic parameter M, heat generation parameter Q and Prandtl number Pr on momentum and heat transfer have been studied in detail. From the present investigation the following conclusions may be drawn:
Ÿ The skin friction coefficient decreases that is the frictional force at the wall reduces for higher values of the Prandtl number Pr, over the whole boundary layer but

Table 1. Comparison of the values of skin friction coefficient, f''(x,0), and the heat transfer coefficient, –q'(x,0) with Hossain et al. [19] and present work for the variation of Prandtl number Pr while Q = 0.0 and g = 0.0 with a = 0.2.
the rate of heat transfer enhances for the same reason.
Ÿ The skin friction coefficient increases that is the frictional force at the wall enhances and the rate of heat transfer reduces for higher values of the heat generation parameter Q.
Ÿ The skin friction coefficient and rate of heat transfer decrease for increasing values of amplitude of the wavy surface a and magnetic parameter M.
Ÿ As the thermal conductivity variation parameter g increases the local rate of heat transfer Nu, the local skin friction coefficient Cf rise up near the leading edge and change their manner for higher values of g in the downstream.
REFERENCES
- L. S. Yao, “Natural Convection along a Vertical Wavy Surface,” ASME Journal of Heat Transfer, Vol. 105, No. 3, 1983, pp. 465-468. doi:10.1115/1.3245608
- S. G. Moulic and L. S. Yao, “Mixed Convection along Wavy Surface,” ASME Journal of Heat Transfer, Vol. 111, No. 4, 1989, pp. 974-979. doi:10.1115/1.3250813
- K. C. A. Alam, M. A. Hossain and D. A. S. Rees, “Magnetohydrodynamic Free Convection along a Vertical Wavy Surface,” International Journal of Applied Mechanics and Engineering, Vol. 1, 1997, pp. 555-566.
- M. A. Hossain and D. A. S. Rees, “Combined Heat and Mass Transfer in Natural Convection Flow from a Vertical Wavy Surface,” Acta Mechanica, Vol. 136, No. 3-4, 1999, pp. 133-141. doi:10.1007/BF01179253
- C. C. Wang and C. K. Chen, “Transient Force and Free Convection along a Vertical Wavy Surface in Micropolar Fluid,” International Journal of Heat and Mass Transfer, Vol. 44, No. 17, 2001, pp. 3241-3251. doi:10.1016/S0017-9310(00)00329-X
- S. Kabir, M. A. Hossain and D. A. S. Rees, “Natural Convection of Fluid with Temperature Dependent Viscosity from Heated Vertical Wavy Surface,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 53, 2002, pp. 48-57. doi:10.1007/s00033-002-8141-z
- J. H. Jang, W. M. Yan and H. C. Liu, “Natural Convection Heat and Mass Transfer along a Vertical Wavy Surface,” International Journal of Heat and Mass Transfer, Vol. 46, No. 6, 2003, pp. 1075-1083. doi:10.1016/S0017-9310(02)00361-7
- J. H. Jang and W. M. Yan, “Mixed Convection Heat and Mass Transfer along a Vertical Wavy Surface,” International Journal of Heat and Mass Transfer, Vol. 47, No. 3, 2004, pp. 419-428. doi:10.1016/j.ijheatmasstransfer.2003.07.020
- M. M. Molla, M. A. Hossain and L. S. Yao, “Natural Convection Flow along a Vertical Wavy Surface with Uniform Surface Temperature in Presence of Heat Generation/Absorption,” International Journal of Thermal Sciences, Vol. 43, No. 2, 2004, pp. 157-163. doi:10.1016/j.ijthermalsci.2003.04.001
- B. Tashtoush and M. Al-Odat, “Magnetic Field Effect on Heat and Fluid Flow over a Wavy Surface with a Variable Heat Flux,” Journal of Magnetism and Magnetic Materials, Vol. 268, No. 3, 2004, pp. 357-363. doi:10.1016/S0304-8853(03)00547-X
- L. S. Yao, “Natural Convection along a Vertical Complex Wavy Surface,” International Journal of Heat and Mass Transfer, Vol. 49, 2006, pp. 281-286. doi:10.1016/j.ijheatmasstransfer.2005.06.026
- M. Ali, A. Alim and L. S. Andallah, “Conjugate Effects of Radiation and Joule Heating on Magnetohydrodynamic Free Convection Flow along a Sphere with Heat Generation,” American Journal of Computational Mathematics, Vol. 1, No. 1, 2011, pp. 18-25. doi:10.4236/ajcm.2011.11003
- M. Patel and M. G. Timol, “Magneto Hydrodynamic Orthogonal Stagnation Point Flow of a Power-Law Fluid Toward a Stretching Surface,” American Journal of Computational Mathematics, Vol. 1, No. 2, 2011, pp. 129- 133.
- N. Parveen and M. A. Alim, “Joule Heating Effect on Magnetohydrodynamic Natural Convection Flow along a Vertical Wavy Surface with Viscosity Dependent on Temperature,” International Journal of Energy & Technology, Vol. 3, 2011, pp. 1-10.
- W. M. Kays, “Convective Heat and Mass Transfer,” McGraw-Hill, New York, 1966, p. 362.
- M. A. Hossain, M. S. Munir and D. A. S. Rees, “Flow of Viscous Incompressible Fluid with Temperature Dependent Viscosity and Thermal Conductivity past a Permeable Wedge with Uniform Surface Heat Flux,” International Journal of Thermal Sciences, Vol. 39, No. 6, 2000, pp. 635-644. doi:10.1016/S1290-0729(00)00227-1
- H. B. Keller, “Numerical Methods in Boundary Layer Theory,” Annual Review of Fluid Mechanics, Vol. 10, 1978, pp. 417-433. doi:10.1146/annurev.fl.10.010178.002221
- T. Cebeci and P. Bradshaw, “Physical and Computational Aspects of Convective Heat Transfer,” Springer, New York, 1984.
- M. A. Hossain, S. Kabir and D. A. S. Rees, “Natural Convection of Fluid with Temperature Dependent Viscosity from Heated Vertical Wavy Surface,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 53, 2002, pp. 48-52. doi:10.1007/s00033-002-8141-z
Nomenclature
Cf local skin friction coefficient Cp specific heat at constant pressure [J·kg–1·K–1]
f dimensionless stream function g acceleration due to gravity [ms–2]
Gr Grash of number L characteristic length associated with the wavy surface [m]
M magnetic parameter
 unit normal to the surface Nu local Nusselt number P pressure of the fluid [Nm–2]
unit normal to the surface Nu local Nusselt number P pressure of the fluid [Nm–2]
Pr Prandtl number Q heat generation parameter Q0 heat generation constant
 heat flux at the surface [Wm–2]
heat flux at the surface [Wm–2]
T temperature of the fluid in the boundary layer [K]
Tw temperature at the surface [K]
T¥ temperature of the ambient fluid [K]
u, v dimensionless velocity components along the (x, y) axes [ms–1]
x, y axis in the direction along and normal to the tangent of the surface
Greek Symbols
a amplitude of the surface waves
β volumetric coefficient of thermal expansion [K–1]
g thermal conductivity variation parameter
η dimensionless similarity variable q dimensionless temperature function k thermal conductivity [Wm–1·K–1]
k¥ thermal conductivity of the ambient fluid [Wm–1·K–1]
m viscosity of the fluid [kgm–1·s–1]
μ¥ viscosity of the ambient fluid
ν kinematic viscosity [m2·s–1]
r density of the fluid [kg·m–3]
σ0 electrical conductivity
σ(x) surface profile function tw shearing stress y stream function [m2·s–1]

