Received 10 July 2014; revised 12 August 2014; accepted 2 September 2014

ABSTRACT

‘t Hooft-Veltman Wilson dimensional regularization depends crucially upon Borel summability which entails strong links to the modern mathematical theory of transfinite sets and consequently to the fractal-Cantorian spacetime proposal of Ord-Nottale-El Naschie. Starting from the above, we interpret the main step of the mathematical analysis in terms of elementary particles interaction. Thus ‘t Hooft-Veltman “perturbation” parameter which measures the deviation of the regulated space from the four dimensionality of spacetime is interpreted as an elementary particle with a topological mass charge equal to 0.18033989, i.e. double the magnitude of Hardy’s quantum entanglement. In turn, Hardy’s quantum entanglement which may be interpreted geometrically as a consequence of the zero set embedded in an empty set could also be interpreted as an exchange of pseudo elementary particles with a topological mass charge equal to Hardy’s entanglement where is the Hausdorff dimension of the zero set of the corresponding ‘t Hooft-Veltman spacetime.

Keywords:

A New Dimensional Regularization Particle, ‘t Hooft Fractal Spacetime, Hardy Quantum Entanglement, E-Infinity Cantorian Spacetime, Disintegration of the Vacuum

1. Introduction

‘t Hooft-Veltman-Wilson dimensional regularization is a highly successful method in its analytical form as well as in the computerized counterpart extensively used in solid state physics [1] -[12] . It is generally known that the three Nobel Laureates mentioned above occasionally asked themselves if the use of for spacetime where much smaller than unity could imply that spacetime may be a fractal at the quantum scale [4] - [14] . In fact the present author knows firsthand that G. ‘tHooft and at the time his thesis Adviser, M. Veltman debated this issue but did not come to any conclusive result [4] [5] [7] . Historians of science may well debate the issue of why this relatively small step from 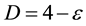to a fractal spacetime described by a Hausdorff dimension was not discovered much earlier i.e. at the same time when the renormalizability of the Yang-Mills theory was discovered [2] [8] . A possible explanation and we stress that it is only a possibility, may be that the intimate link between Borel summability and fractals was not obvious. However the fact is that Emil Borel in France [15] was quite an expert on the essence of fractals long before it was popularized and named fractals by B. Mandelbrot [16] . It is a firm historical fact that G. Cantor’s ideas and his transfinite set theory survived the onslaught of the mainstream at the time and moved from there to France and finally found a dedicated group which established the famous Moscow School of Mathematics [15] led by Egerove. Many of the towering figures of modern mathematics were members of this school and we may mention here the names of a few who had considerable influence on the development of mathematics and theoretical physics in general and E-infinity Cantorian spacetime in particular, namely Kolmogorov, Suslin and Urysohn (see E-infinity communications [17] ). Equipped with the mathematical machinery of E-infinity theory and having some knowledge of quantum field theory and ‘t Hooft’s method it was relatively easy for the present author to discover the almost one to one correspondence of dimensional regularization and the Cantorian-fractal theory of high energy physics [17] - [20] . We stress once more that the subtlety of dimensional regularization lies in the application of Borel’s method for treating divergence and that is where Cantor sets and KAM theorem [16] enters into the subject leading to the inescapable conclusion that ‘t Hooft-Veltman-Wilson method implies a Cantorian fractal spacetime and what more exciting also to a host of exotic new elementary particles [21] - [23] as we hope to show in the following main part of the ensuing sections of the present short paper.

2. Dimensional Regularization and Dark Energy

First To avoid troublesome singularities and to be able to extract a finite answer from an otherwise diverging series, dimensional regularization resorts to some ingenious mathematics due to E. Borel [24] [25] . Not only that but the mathematical scheme would also require that one thinks of the four dimensionality of our spacetime as being slightly less than 4, namely 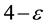where 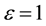will play the role of an order parameter, i.e. more or less a perturbation parameter [1] - [13] . In E-Infinity we encountered in the context of a fractal Kaluza-Klein [26] the fractal K-K spacetime dimension given by [27]

(1)

This could be considered to approach D = 5 from above with being an order parameter with fixed value

where 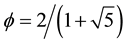as discussed in great detail in [26] [27] . The sparseness of 5 + 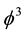compared to 5 was

subsequently reasoned geometrically to be the density of the dark energy of our cosmos provided the K-K fractal theory is an accurate topological description of our universe. In this respect our hope was greatly fulfilled and we were rewarded by a result in full agreement with cosmic measurements and observations as well as all previous derivations, namely [28] [29]

(2)

As mentioned a moment ago the situation with is quite similar and we set to be naturally related to Hardy’s entanglement for a single particle of two entangled Hardy quantum particles, i.e. P(Hardy)/2 = then multiply this value with each of the four dimensions of our spacetime and that way we find 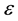namely [4] [5] [27] - [29]

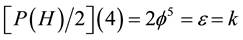(3)

where = 0.18033989. The dark energy density could now be determined as in the K-K theory

to be the ratio of the ‘regulated’ dimension to the original dimension, namely 4. That means [3] [5] [29]

(4)

which is exactly our previous result apart from being what has been measured by WMAP and PLANCK.

The rational question is now to ask what kind of magical number system is involved in the preceding calculation and how come that this numeric fits seamlessly to physics and everything else? This we explain in the next section and we hasten to say that at the end we should find out that the magic is nothing else but the revival of Kantian pure mathematical reasons upon which our very existence is based.

3. Replacing Borel Summation by Suslin Operation and Weyl Scaling

Let us reconsider our last result for which after some simple manipulation could be written as [4] [5] [29]

(5)

Noting that we started with [4] [5] [27] - [29]

(6)

we see that we can let without losing the integer part of our result i.e. Equations (5) and (6). Thus for we have [4] [5]

(7)

and

(8)

However if we had worked from the very beginning with we would have obtained the trivially wrong result, namely

(9)

Again, how is this possible? The short answer is that we used one of the seven pillars of wisdom which is traditionally ignored in physics, namely the number system employed by nature to construct a logical universe [30] - [33] rather than the various mundane number systems which are based on the human experience in dealing with everyday life and that includes the rather rudimentary binary system of digital computers namely of zero and one [30] .

The preceding assertion needs considerable elaboration to be fully or minimally understood. In such a case we could not do better than use a generic example which happens to be the very case we are dealing with here. In essence and in a nutshell, without going into the maize of abstract mathematical arguments characteristic for transfinite se theory, measure theory and the continuum hypothesis the answer is that we will be replacing Borel resummation by what is for physicists, more familiar Weyl scaling [31] .

4. The Main Sequence of E-Infinity Weyl Scaling

As known from E-infinity, differentiation and integration are replaced by down scaling and up scaling respectively [16] -[18] . This is somewhat similar to the replacement of differentiation by a Poisson Bracket and integration with Dixmier trace in A. Connes’ non-commutative geometry [34] . Let us start from the theoretically exact value of the inverse fine structure constant

(10)

For a Cooper pair, we have where and. Scaling down using the fundamental scaling factor [16] one finds the following 6 “quasi-differentiated” sequence [30] - [33]

(11)

Notice we always have an integer plus or minus a multiple of used earlier on to regulate the singularities in ‘t Hooft-Veltman-Wilson method. Thus setting k = 0 we retrieve the Heterotic superstring dimensional hierarchy in full plus the non-super symmetric grand unification inverse coupling constant. The reader should assure himself or herself that taking = 137/2 without the small irrational number will result in a rather messy numerical chain reaction obscuring the neat result found by simply setting k = 0 as we just demonstrated. The preceding result will also encourage us to think seriously about looking at k and consequently also at as well as not only as perturbation book keeping devices or simply unnecessary numbers after the comma which should be better rounded away but as physically meaningful objects such as instantons, texture, domain walls and exotic topological defects as well as other objects resulting from the disintegration of the vacuum discussed by many others including the present one many years ago [23] .

5. Physical-Topological Interpretation of ‘tHooft Order Parameter ε = k = 2f⁵

Define The disintegration of the simplictic vacuum was studied in several earlier publications in connection with paradoxical decomposition and fractal Cantorian spacetime as a source of exotic particles [21] - [23] . Two new particles were identified on this occasion with conjectured mass of 26 Mev and 42 Mev matching those reported in scattered experimental research conducted in Darmstadt as well as Cairo as reported by L. Nottale in his classical book [35] . The most important finding from that period however, at least as far as the present work is concerned, is the conjectured exotic quasi particle with a mass [21] - [33]

M(K) = 0.18033989 Mev (12)

as reported by the present Author in Ref. [22] . In that particular paper we were also concerned with the phenomena of anomalous positron production as well as gravitational instantons again within the basically fractal setting of a symplectic geometry. The incredible coincidence of gauged in Mev is of course no coincidence because even ten years ago [21] we already felt the logical necessity and aesthetic attraction in the sense of Dirac looking at K not only as a geometrical object but as a real physical “quasi” particle. This we elaborate next.

6. Fractal Logic and the Mass Spectrum of the Standard Model

The fuzzy logic related notion of fractal counting of quantum particles which is based on fractal logic [30] was introduced some time ago in connection with the SU(3) SU(2) U(1) standard model of elementary high energy particles [16] . There it was shown how the three particles of SU(2), namely the experimentally found, and should not be counted as 3 but as 2.88543824. The physical meaning of this initially strange proposal becomes more understandable when we see the entire spectrum of all the classical 12 particles. These 12 particles are in fact 14 particles when counted correctly and have the fractal number weight of only

(13)

where = 137.082039325 is the E-infinity exact inverse value of the electromagnetic fine structure constant and is the Hardy-Unruh self entanglement [36] . Consequently putting the 2.88543824 under our transfinite- fractal magnifying glass we see immediately that it is 16 times our dimensional regularization k =, i.e. that used in our interpretation of ‘t Hooft method where D = 4 − and = k = [36] . Consequently we have a highly consistent theory linking in the 16 bosonic dimensions of Heterotic superstring theory with a fractal number of generators of a fuzzy version of the electroweak Lie symmetry group SU(2) [16] [30] . We speculate on passing that there may be a link here between anomalous positron production in ultra strong magnetic fields and to the disintegration of, and into 16 exotic quasi particles [21] - [23] . In this respect it is wise to ponder very deeply the unexpected result of fractal “fuzzy” logic as applied to the 12 gauge bosons of the classical standard model where it was revealed in [30] that the 12 particles are really 14 particles with fractal weight equal 11.7082039325 particles! In particular two particles with the topological charge or weight 16k + k² turn out to be equal 3 − k_o as an elementary computation easily reveal which is a fractal spatial dimension found from some fundamental equations.

7. Conclusions

With the benefit of hindsight we see that the present result, i.e. the existence of an exotic quasi particle M(k) = 2ϕ⁵ where ϕ⁵ is Hardy’s generic value for the entanglement of two quantum particles [36] should have been expected all along and not only after realizing that ‘t Hooft-Veltman-Wilson

spacetime is essentially a fractal spacetime. For instance we have known for decades that the arithmetic mean of the sum of the masses of the charged and the neutral π-meson is to a high accuracy equal to the magnitude of the inverse electromagnetic fine structure constant gauged in Mev. Similar observations were made with regard to K-meson, the proton as well as the famous empirical relation between the mass of the electron and that of the proton and neutron [16] [37] -[39] .

In view of all the aforementioned, we cannot hesitate to express our strong view that quantum spacetime is a Cantorian fractal manifold and that without this fact, dimensional regularization could not be applied in the way it is applied and would not have given the right answer to the problem at hand as it did and in full agreement with measurements and observations.

References