World Journal of Nuclear Science and Technology
Vol.3 No.4(2013), Article ID:37606,7 pages DOI:10.4236/wjnst.2013.34023
Absolute Neutron Activation Analysis Technique of a Large Crude Oil Sample
Nuclear Physics Department, Petersburg Nuclear Physics Institute, Saint Petersburg, Russia
Email: pitzinovjev@yandex.ru
Copyright © 2013 V. G. Zinovyev et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 21, 2013; revised July 29, 2013; accepted August 11, 2013
Keywords: Neutron Flux; Neutron Activation Analysis; ENDF Datab
ABSTRACT
This manuscript presents an application of calculation methods in neutron activation analysis (NAA) of a large crude oil sample. Monte-Carlo computer code was developed. The computer code calculates neutron cross sections and neutron flux density distribution in the interior large sample. ENDF/B-VII.0 data files and ENSDF BNL-NCS-51655-01/02-Rev data files were used as nuclear databases in our computer code. HPGe planar detector efficiency registration technique and the software were developed for the absolute NAA technique of the large sample. The concentrations of Na, K, Ca, Sc, Cr, Fe, Co, Ni, Cu, Zn, Ga, As, Br, Sr, Zr, Mo, Ag, Sb, Cs, Ba, Ce, Nd, Sm, Eu, Tb, Dy, Ho, Tm, Yb, Lu, Hf, Ta, W, Pt, Au, Hg, Th and U in the crude oil samples of Eastern Siberia oilfield were determined using calculation and relative techniques in the concentration range from 10−9 to 0.5%.
1. Introduction
The rapid development in the last few decades of power engineering and industry throughout the world, has led to increase consumption of crude oil and petroleum product. Elements Fe, Co, Ni, V, W, Mo, Pt, Pd are catalysts and N, P, As, Sb, Bi, O, S, Se, Te are paralysts of crude oil dissociation. Trace concentrations of these elements have an effect on the petroleum refining process. The concentration ranges of the elements (Co, Ni, Fe, V, W, Mo, Pt, Pd) are 10−9% - 10−4%. During the last five years at our institute, studies have been conducted on the application of nuclear-physical methods of analysis to determine impurity content of crude oil samples. Neutron activation analysis, X-ray fluorescent analysis (XRF), and prompt gamma neutron activation analysis (PGNAA) were used as study methods. In our work, the NAA has high sensitivity and the ability to determine a large number of elements in one series of analysis.
NAA was used as an analytical method for the determination of impurities in the crude oil samples from Siberia oilfields. Usually the NAA is performed in pointsource geometry for decrease of neutron self shielding effect. Intensity of gamma ray (sensitivity of NAA method) can be increased by using of the large samples (weight about 100 g). An increase in the number of determined elements and the improvement of the detection limits (DL) has been achieved using large oil sample (LOS) NAA.
Monte Carlo method was used for assessing gammaand neutron-transport in samples. The Monte Carlo method is a probabilistic one that follows the path of a particle from its creation to death, simulating all its interactions. The result is an ability to accurately model complex systems. Hussein et al. [1] utilized Monte Carlo method to model the measurement of chlorine with prompt gamma-ray neutron activation analysis. Maurec [2] also used it to assess the neutron and gamma flux distribution in soils saturated with fresh water, salty water, and oil. We used this method to determinate neutron flux density distribution and activity distribution into large crude oil samples. Our studies were carried out under IAEA project “Application of Large Sample Neutron Activation Analysis Techniques for Inhomogeneous Bulk Archaeological Samples and Large Objects,” research contract 15249.
2. Description
Computer code of activation large cylindrical crude oil sample was developed. The program calculates (n, γ), (n, n), (n, f) nuclear reactions cross-section of sample material with ENDF/B-VII.0 data files and the program calculates thermal and epithermal neutron flux density distribution in the sample with the Monte-Carlo method. The program takes resolved resonance data from ENDF data file of section 151. The subroutine that computes Single-Level Breit-Wigner (SLBW) cross-sections uses next equations [3,4]:
Elastic Scattering Cross Sections were calculated with the next equation for resolved resonance
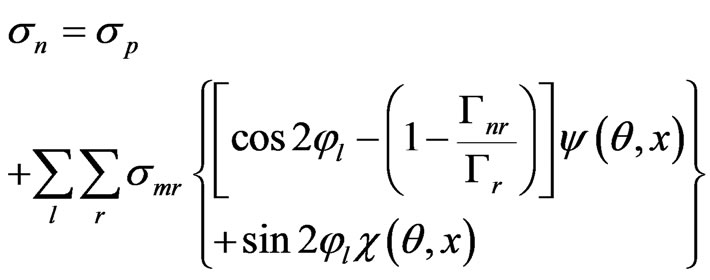
Radiative Capture Cross Section was calculated as
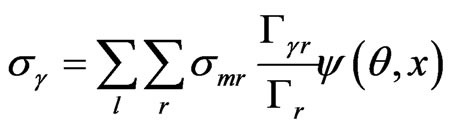
Fission Cross Section was calculated by equation
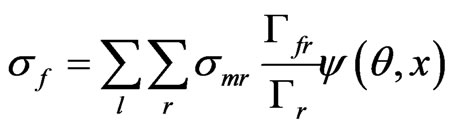 .
.
where Γnr—neutron width, Γγr, the radiative capture width, Γfr—the fission neutron width, Γr—total neutron width, l—orbital moment, J—the spin, or total angular momentum, of the resonance.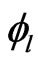 —hard-sphere phase shifts.
—hard-sphere phase shifts.
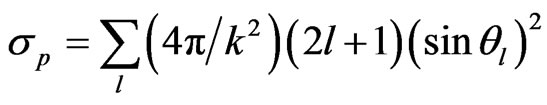 is the neutron potential scat Tering components of the cross section.
is the neutron potential scat Tering components of the cross section.
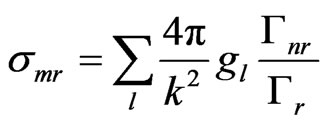 —maximum cross-section value of the resonance.
—maximum cross-section value of the resonance. 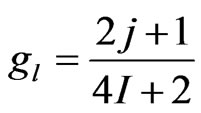 is the spin statistical factorgJ is obtained from the target spin I and the resonance spin J,
is the spin statistical factorgJ is obtained from the target spin I and the resonance spin J, 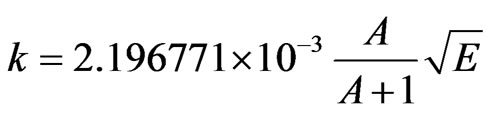 is the neutron wave number, which depends on incident energy E and the atomic weight ratio to the neutron for the isotope A (AWRI in the ENDF file).
is the neutron wave number, which depends on incident energy E and the atomic weight ratio to the neutron for the isotope A (AWRI in the ENDF file).
The resonance line shapes is variated with temperature. The line shape functions ψ and χ determined the temperature dependence with 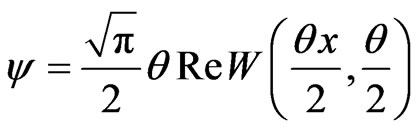 and
and 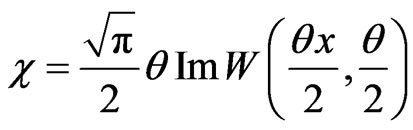 . Where
. Where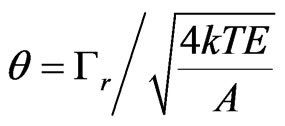 , T is absolute temperature, k is the Boltzmann constant, E is incident neutron energy, x given with
, T is absolute temperature, k is the Boltzmann constant, E is incident neutron energy, x given with 
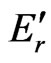 is primed resonance energy.
is primed resonance energy.
Multi-Level Breit-Wigner (MLBW) resonance is described by the same equation as SLBW except that resonance-resonance interference term is included in the equation for elastic scattering of l-wave neutrons
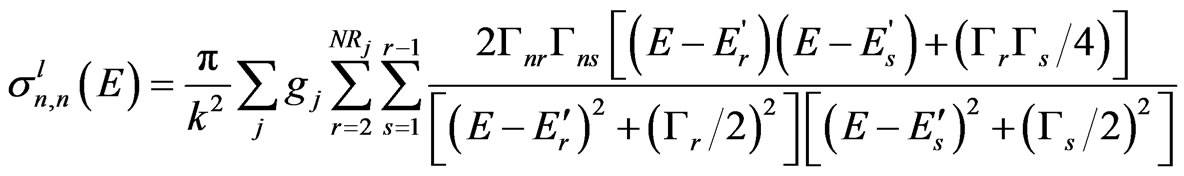
Angular distribution of secondary particles has been made. Angular distributions of emitted neutrons are used for elastically scattered neutrons, and for the neutrons resulting from discrete level excitation due to inelastic scattering. Probability that a particle of incident energy E will be scattered into the interval dμ about an angle whose cosine is μ given by
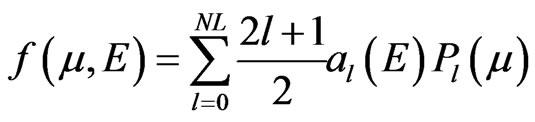
where: μ—cosine of the scattered angle in either the laboratory or the center-of-mass system, E—energy of the incident particle in the laboratory system, l—order of the Legendre polynomial al the l-th Legendre polynomial coefficient, Pl(µ) is penetration factor.
Program verification has been executed using MCNP4C computer code and experiment. Following conditions were taken as initial data to calculate the neutron flux density distribution into sample: sample form was cylinder (Ø4.95 cm, H = 12.5 cm), sample material was NaCl (ρ = 1.38 g/cm3). The sample was irradiated with the isotropic Maxwell neutron flux f = 1013 s∙m−2∙s−1 at T = 293 K. Radial neutron flux density distribution was calculated with our program and MCNP4C computer code into sample, Figure 1.
Figure 2 shows experimental and calculation thermal neutron flux radial distribution inside NaCl sample.
HPGe planar detector efficiency registration technique and software for the absolute NAA technique of the large sample are developed. The correct registration of an activity is a very important problem for absolute NAA. Registration geometry is given in Figure 3.
For the sake of mathematical simplicity are taken a = R. The detector efficiency calculation is based on the formula [5]:
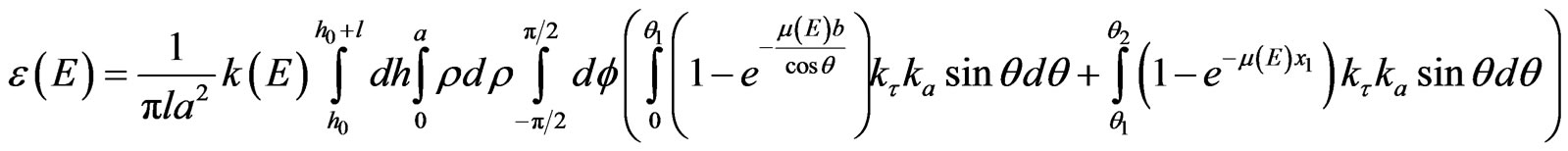
where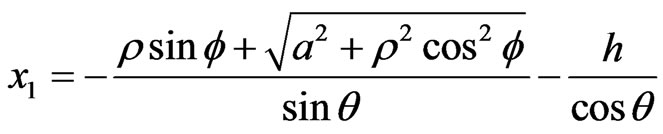 ;
;
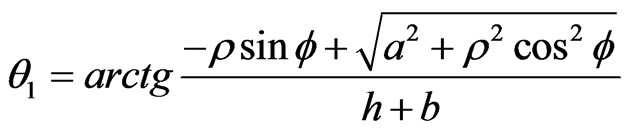 and
and
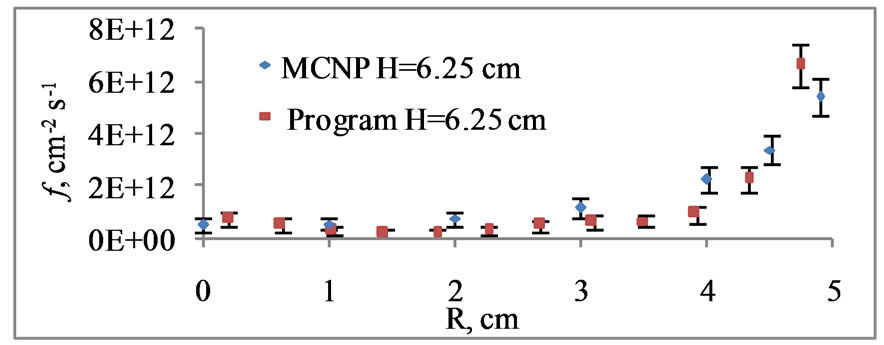
Figure 1. Neutron flux density distribution is obtained with MCNP4 computer code and our program.
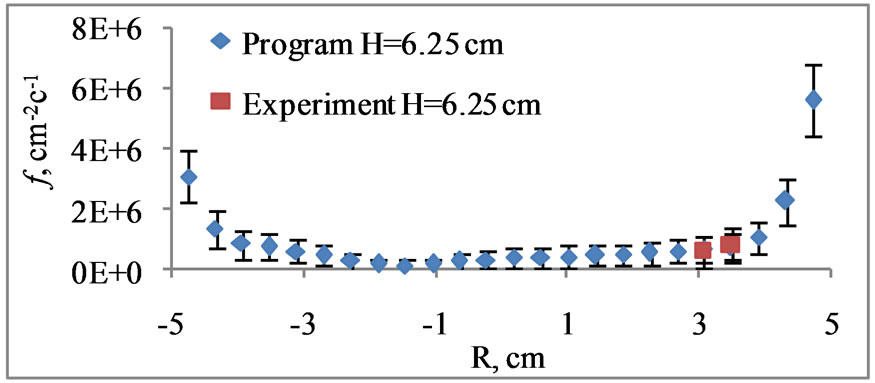
Figure 2. Experimental and calculation thermal neutron flux radial distribution inside NaCl sample. Sample weight 1.35 kg, sample height 12.5 cm, Ø9.9 cm. Flux monitorscontainer bottom distance was 6.5 cm.
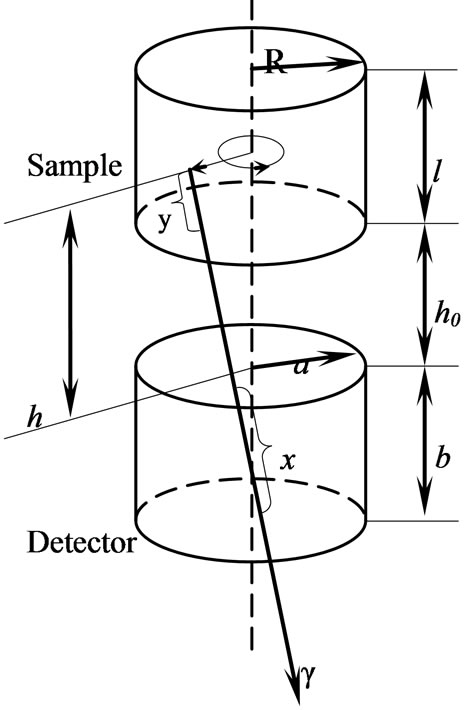
Figure 3. Registration geometry of large sample. x and y— distance travelled by γ-rays through the detector and sample respectively. a and R are detector and sample radius respectively. b and l are detector and sample height respectively. h0 is detector-sample distance.
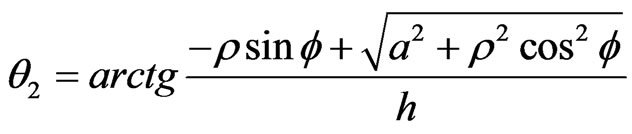 ;
;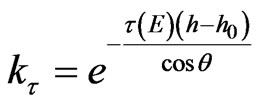 ;
; 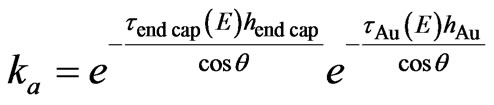
ε(E) is total absolute efficiency with which the Ge crystal detects γ-rays of energy E, μ(E) is total linear absorption factor of Ge detector, τ(E) is total linear absorption factor of sample. k(E) factor to take into account contribution of the Compton effect in the registration efficiency, kτ is gamma ray absorption factor of the sample material, ka is factor take into account the gamma ray absorption in end cap of detector and gold cover; τend cap(E) and τAu(E) Al or Be and Au absorption factor respectively; hend∙cap and hAu are the end cap and golden cover thickness of the detector respectively.
The k(E) factor has been calculated as a deviation of experimentally received ε(E) values from calculated εc(E) values for the point standard 152Eu source. Registration efficiency of the point source was calculated by equation:
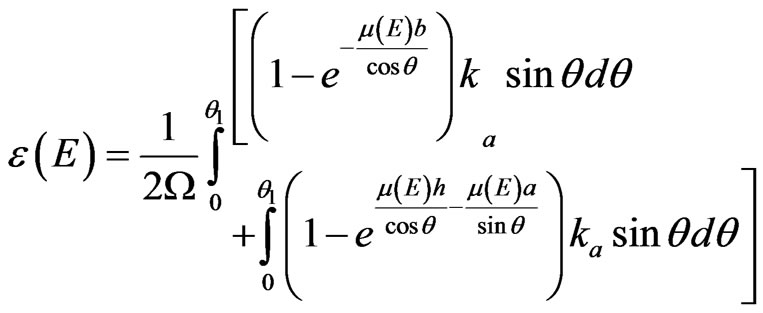
where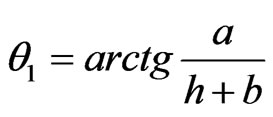 ;
;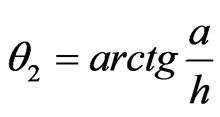 ;
;
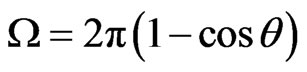 —solid angle of the detector.
—solid angle of the detector.
Calculated and experimental curves of detector efficiency are given in Figure 4 for a large sample (R = 1.1 cm, l = 9 cm, h0 = 3.5 cm). Experimental data were obtained by using water solution of europium salt (152Eu).
3. Experimental Part
The analyses of the crude oil samples are performed using two methods. The large samples are analyses with calculated NAA technique and aliquots of the large crude oil sample are studied with routine INAA (sample mass about 50 - 100 mg).
The calculated NAA technique. We used MDKT1, MDKT2, MDKT3 reference materials (Russia) in our work to verification of the calculation NAA technique. Mass of sample and comparison standard are about 100g. Al(99.9%)-Co(0.1%) and Al(99.9%)-Au(0.1%) alloys were used as thermal and epithermal flux monitors. Ni foil (0.1 mm) is used as fast neutron flux monitor. Samples and comparison standards are packed up into quartz glass containers, Figure 5. Containers have a capillary. The capillary provides reduction of a pressure at an irradiation. Flux monitors are distributed over height and perimeter of the container uniform. Large samples, comparison standard and flux monitors are irradiated into the dry channel (V14) which locates outside the beryllium reflector. Thermal neutron flux is n × 1012 cm−2c−1. The f thermal to epithermal flux ratio is 45. The α epithermal flux deviation from the ideal (1/E) distribution is determined with the “Cd ratio” method (Au, Co monitors) [6]. The result of measurement was 0.023 with uncertainty of 10%. Irradiation time was two-hour.
Samples and reference materials were repacked into clean weighing bottles after irradiation.
The relative NAA technique. Aliquots of the large crude oil sample and IAEA 433 reference material were
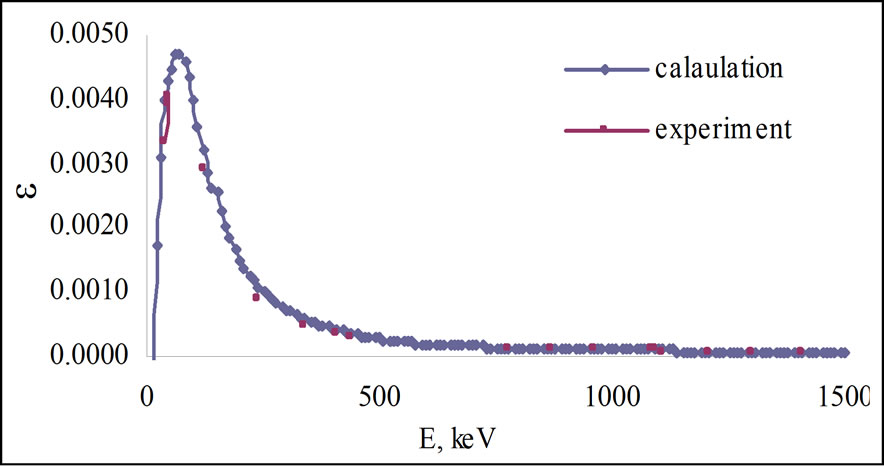
Figure 4. Calculated and experimental curves of planar detector efficiency for the large sample (R = 1.1 cm, l = 9 cm, h0 = 3.5 cm).

Figure 5. Quartz glass containers are used to irradiate of large crude oil samples.
packed in high-purity quartz glass ampoules. Sample mass and comparison standard mass were about 50 - 100 mg. The irradiations were carried out in a water channel of WWR-M reactor, for 2 h, at fth = 4 × 1013 cm−2s−1 and fepi = 2 × 1012 cm−2s−1. α parameter was 0.028 with uncertainty of 10%.
Sample and comparison standard activity was measured with the 15% coaxial HPGe detector (Canberra, FWHM 1.7 keV at Eγ = 1332.5 keV) for the registration of high-energy gamma-rays and with the thin planar HPGe-detector (DSGmbH PSP 1000-13, FWHM 0.9 keV at Eγ = 122 keV) for the registration of low-energy gamma-rays. The gamma-ray spectra were measured after 1, 7 and 15 days of cooling time.
4. Results and Discussion
Relative and calculation NAA techniques were used for determination of Na, K, Cr, Fe, Co, Zn, As, Br, Mo, Ba, La, W, Au, and Hg in sample of Salimskaya oilfield. Analysis results of the oil sample are given in Table 1.
Monte-Carlo computer code was used to determine neutron flux density distribution into the sample. Activity of the analytical nuclide was defined by
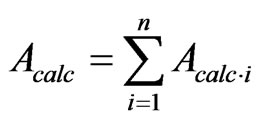
into sample in this case. Acalc∙i, is activity of the nuclide into i-th elementary cell, n is quantity of elementary cells into sample. Mass fraction (%) of a defined element is calculated by equation

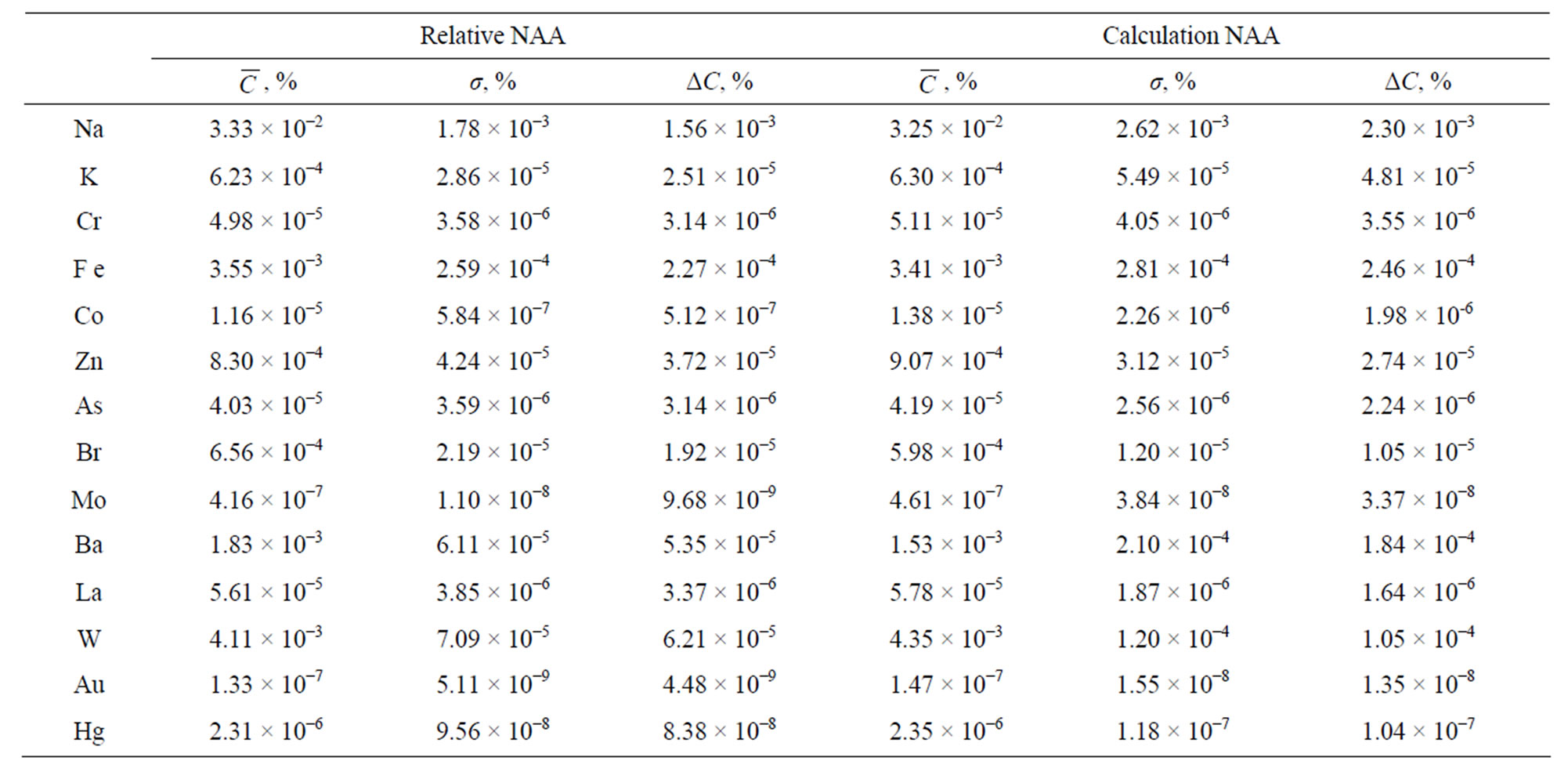
Table 1. Concentrations of elements in the Salimskaya oilfield sample are determined by relative and calculation NAA techniques. 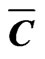 is average value of the element concentration; σ is standard deviation; ΔC is confidence interval. Significance level of measuring results was α = 0.05.
is average value of the element concentration; σ is standard deviation; ΔC is confidence interval. Significance level of measuring results was α = 0.05.

Table 2. The description of oil samples.
where A is the experimental activity of analytical isotope of the defined element in the sample, n is quantity of elementary cells into sample, p is the isotope abundance, M is the atomic weight of the element, mi is mass of an elementary cell, Na is Avogadro number, 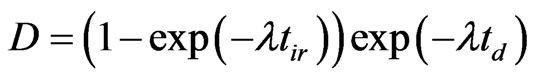 is irradiation and cooling time factor, tir and td are irradiation and cooling time respectively, λ = ln(2)/T1/2, Т1/2 is half-life of the analytical isotope. fth∙i and fepi∙i are thermal and epithermal neutron flux into i-th elementary cell that were calculated by Monte-Carlo computer code. σth is thermal cross-section. I(α) is determined by
is irradiation and cooling time factor, tir and td are irradiation and cooling time respectively, λ = ln(2)/T1/2, Т1/2 is half-life of the analytical isotope. fth∙i and fepi∙i are thermal and epithermal neutron flux into i-th elementary cell that were calculated by Monte-Carlo computer code. σth is thermal cross-section. I(α) is determined by

where I0 is resonance integral of the isotope and  is
is


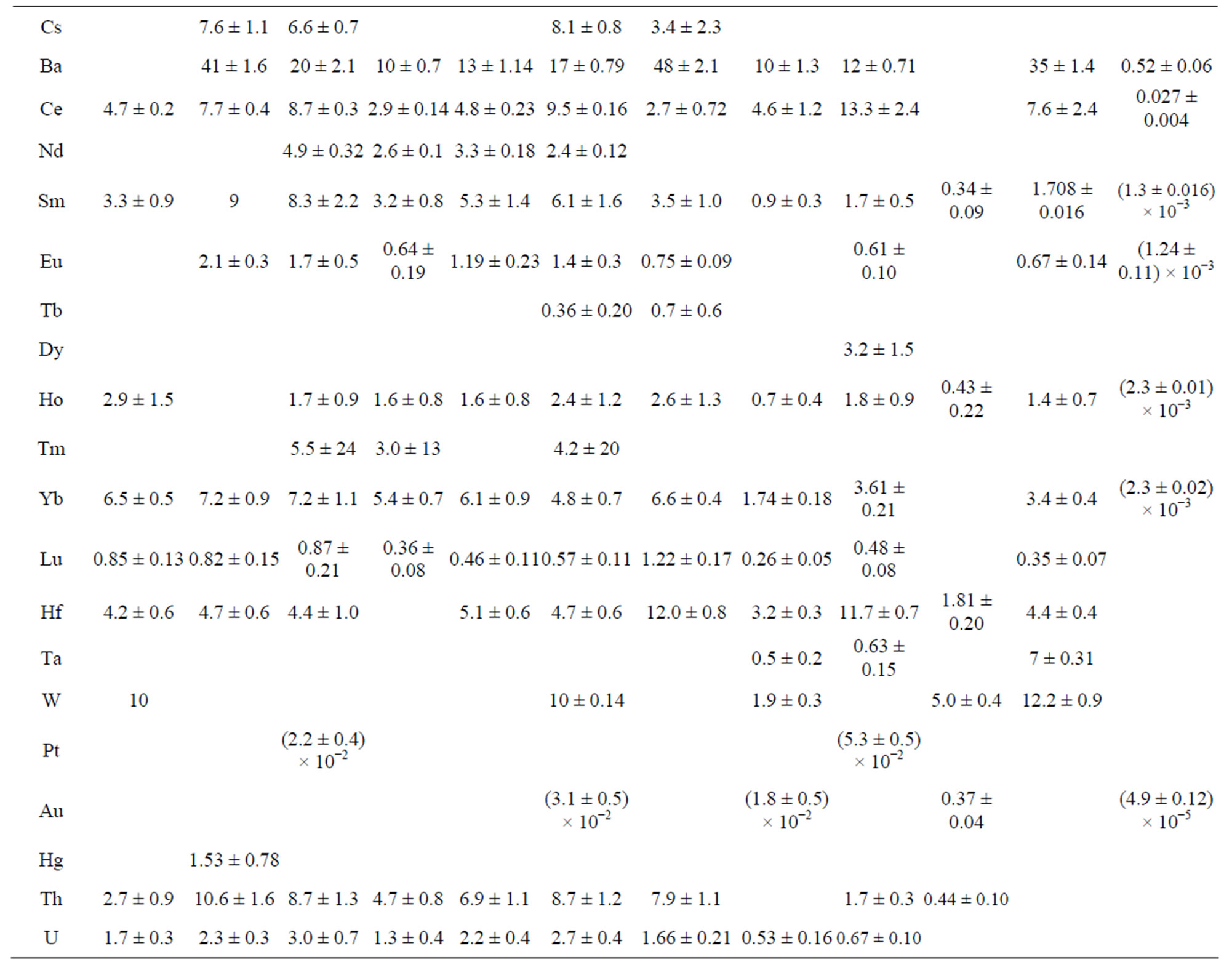
Table 3. The description of oil samples.
effective resonance energy [6,7]. From the activation equation
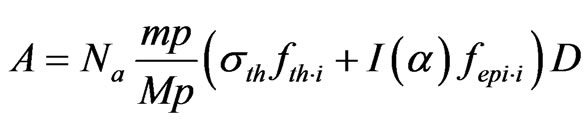 the activity produced per gram of element can be calculated. The minimum activity required to enable measurement with a desired statistical precision can be estimated for example, following the equations given by Gerhard Erdtmann [6]
the activity produced per gram of element can be calculated. The minimum activity required to enable measurement with a desired statistical precision can be estimated for example, following the equations given by Gerhard Erdtmann [6]
 and one obtains for the limit for quantitative determination
and one obtains for the limit for quantitative determination
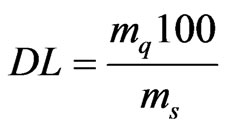
where Aq is the activity, which can be measured with a requisite precision. According to Erdtmann it is
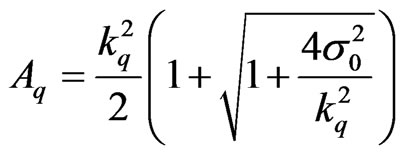
where kq is the reciprocal value of the requisite relative standard deviation and σ0 is the standard deviation of the background measurement.
5. Conclusion
Relative and calculation NAA techniques were developed. Large and routine crude oil samples of East Siberian oilfields were analyzed in our work. We have obtained the concentrations of thirteen eight elements in the samples. Comparison of the relative and absolute results shows that a confidence interval is better at a relative method. However, the calculation technique has better limit determination and is not limited with presence of reference materials, and we can define more elements using this technique. Analysis result of several samples is
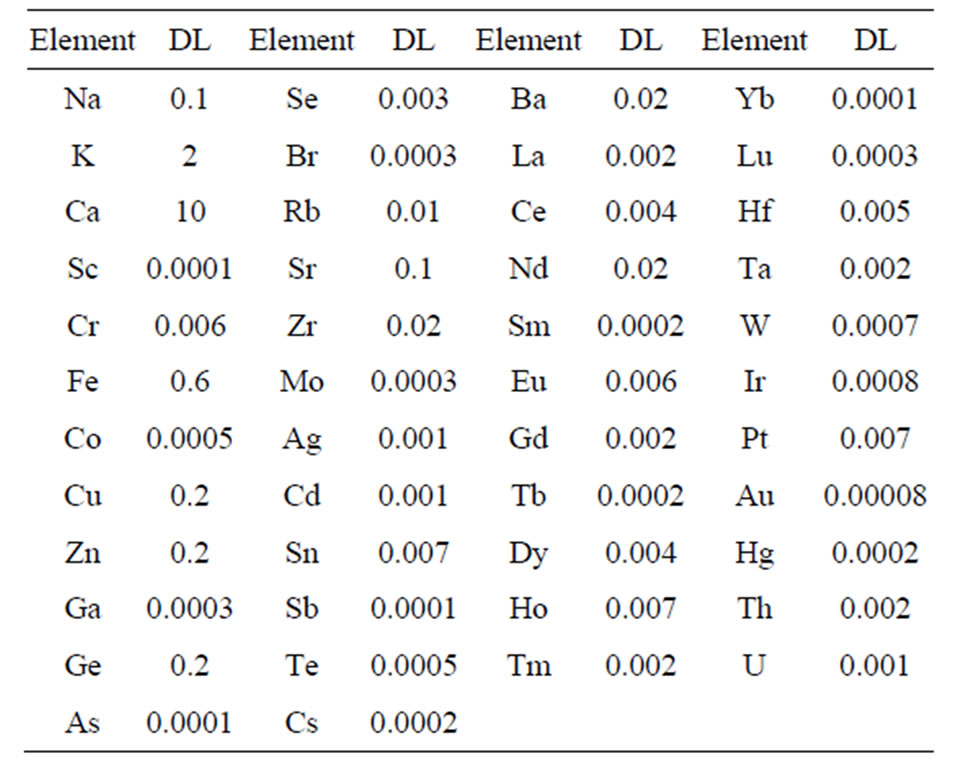
Table 4. Determination limits of NAA for large oil samples, ppm.
given in Table 3. Sample description is given in Table 2. Determination limits of elements are given in Table 4 for large crude oil samples.
REFERENCES
- O. Doron, L. Wielopolski and S. Biegalski, “Advantages of Mesh Tallying in MCNP5 for Soil Analysis Calculations,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 276, No. 1, 2008, pp. 183-186.
- M. Maurec, “Implementation of Variance-Reduction Techniques for Monte Carlo Nuclear Logging Calculations with Neutron Sources,” Radiation Protection Dosimetry, Vol. 116, No. 1-4, 2005, pp. 498-503. http://dx.doi.org/10.1093/rpd/nci245
- R. E. Mac Farlane and A. C. Kahler, “Methods for Processing ENDF/B-VII with NJOY,” Nuclear Data Sheets, Vol. 111, No. 12, pp. 2739-2890.
- S. F. Mughabghab, “Atlas of Resonance Parameters and Thermal Cross Sections, Z = 1-100,” Elservier, Amsterdam, 2006.
- N. A. Vartanov and P. S. Samoylov, “Applied Scintillation Spectrometry,” Atomizdat, Moscow, 1975, p. 408.
- G. Erdtmann and H. Petri, “Nuclear Activation Analysis: Fundamentals and Techniques,” Treatise on Analytical Chemistry, Vol. 14, No. 1, New York, 1986, p. 643.
- F. De Corte and A. De Wispelaere, “The Use of a Zr. Au. Lu Alloy for Calibrating the Irradiation Facility in k0- NAA and for General Neutron Spectrum Monitoring,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 263, No. 3, 2005, pp. 653-657. http://dx.doi.org/10.1007/s10967-005-0639-3

