World Journal of Nuclear Science and Technology
Vol.2 No.4(2012), Article ID:23773,4 pages DOI:10.4236/wjnst.2012.24022
Differential Cross Section of Electron Scattering from 3He and 3H Nuclei with Considering Pionic Contribution
1Department of Physics, University of Azad Tehran Markaz, Tehran, Iran
2Department of Physics, University of Mohaghegh Ardabili, Ardabil, Iran
Email: *Zolfagharpour@uma.ac.ir
Received June 28, 2012; revised July 31, 2012; accepted August 15, 2012
Keywords: Pionic Contribution; Structure Function; Differential Cross Section
ABSTRACT
The excess pion inside the nucleus could change not only nucleons structure function, but also electron scattering cross section from nuclei. In this paper, we calculate pionic contribution in nuclear structure functions of 3He and 3H nuclei and the differential cross sections of electron scattering from these nuclei. At first, we calculate the Fermi motion and binding energy contribution as an important nuclear medium effect in scattering cross sections and then we add pionic contribution to structure functions and differential cross sections of electron scattering from these nuclei that the Fermi motion and binding energy are considered.
1. Introduction
One of the important questions in nuclear physics is difference between a free nucleon structure function with a bound nucleon structure function. In this paper, we have investigated one of the main reasons of this difference in nucleus structure function in 0.1 ≤ x ≤ 0.3 range by considering pion sea around nucleons inside nucleus. A nucleus consists of nucleons, mesons, and objects like ∆ particle [1]. Nucleons and mesons made of quarks and sea quarks. Quarks inside both of nuclei and mesons could not be marked and distinguished, so the electron scattering from bound nucleons are different from free nucleons [2-4]. Therefore, the free nucleon structure function is different from bound nucleon structure function. Pions are the lightest mesons, and presences of them in a nucleus are more than other mesons. So, we investigate presence of pions in nucleus. Since, a free nucleon is a particle that virtual pions embedded around nucleons and creating a pion cloud around nucleons. When a nucleon is inside nuclei, pion cloud is increasing around the nucleon. When electrons scatter from nuclei, the probability of the interaction between a virtual photon of incident electrons with a bound nucleon is increasing, because interaction between virtual photon with pions is increasing. The virtual photon scatters from not only a quark insides nucleons, but also a quark or sea quark from pion cloud [5]. This effect is obvious in range x ≤ 0.2. Therefore, pion cloud plays a role in nuclei structure functions. In this paper, first, we calculate pionic contributions in 3He and 3H nuclei, and then we calculate cross sections by considering these contributions.
2. Pion Structure Function
The nucleus structure function, in nuclear conventional theory, with respecting the pion cloud effect is [5]:
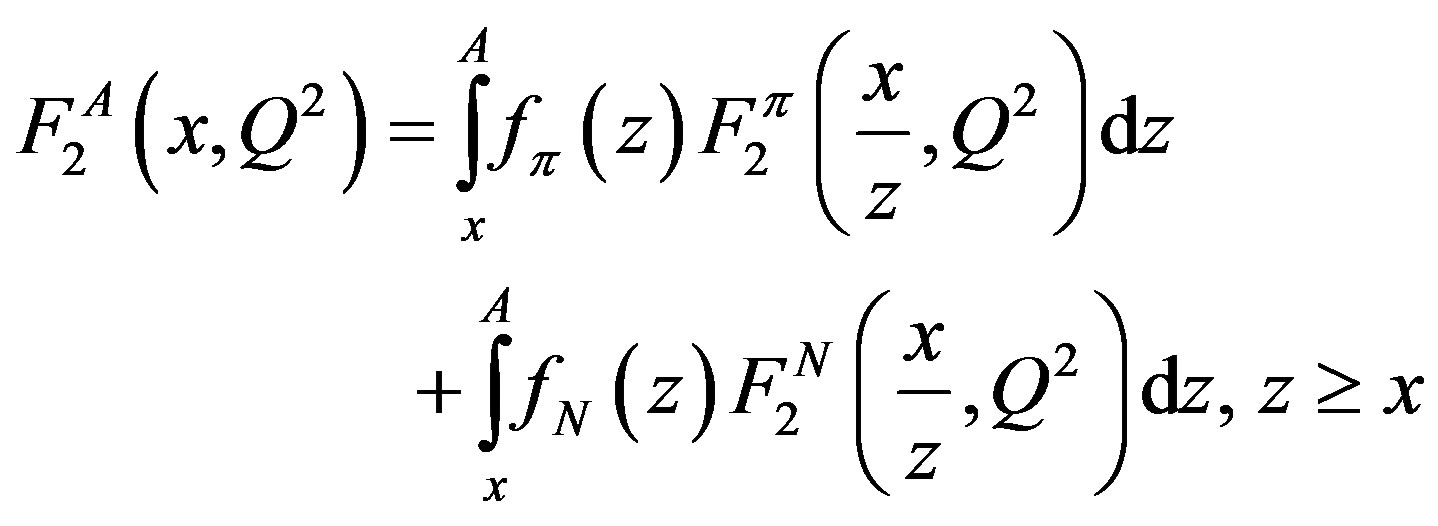 (1)
(1)
First term indicates the pionic contribution and the next term indicates the nucleon contribution in the nucleus. First term contribution is noticeable around . x is Bjorken variable. z is the light-cone momentum fraction of the nucleus carried by nucleon, and its distribution is inside nucleus
. x is Bjorken variable. z is the light-cone momentum fraction of the nucleus carried by nucleon, and its distribution is inside nucleus  taken from [6].
taken from [6]. 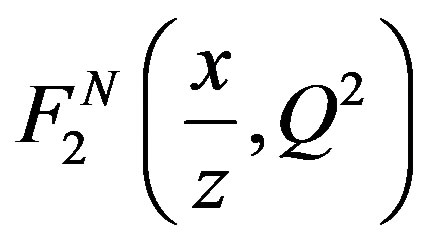 is the nucleon structure function [7]. The momentum distribution
is the nucleon structure function [7]. The momentum distribution 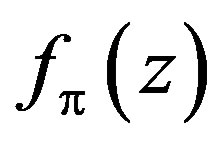 in a free nucleon case is given as follow [8]:
in a free nucleon case is given as follow [8]:
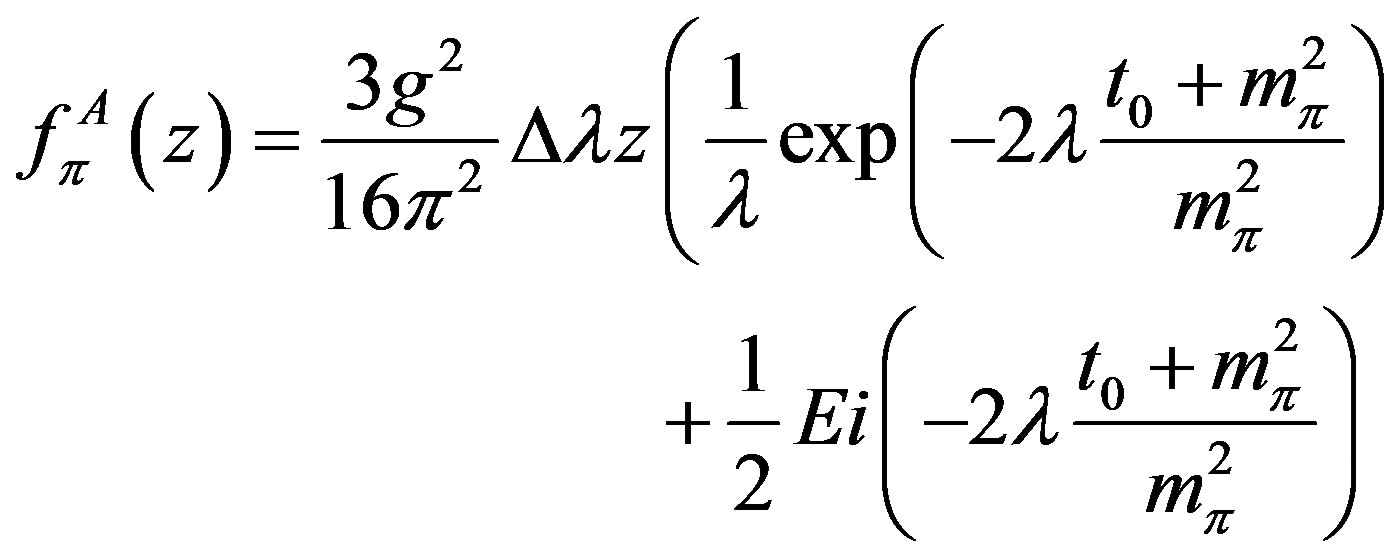 (2)
(2)
where
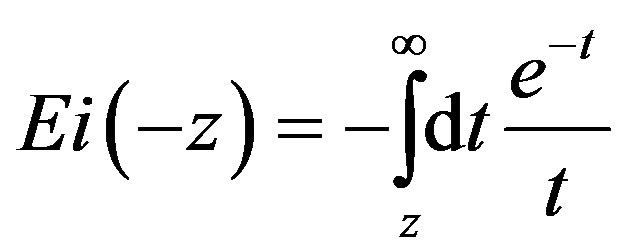 (3)
(3)
which g = 13.5 is the coupling constant. The cut off parameter λ plays the most substantial role. When the nucleon is embedded in a nucleus, several modifications such as the polarization of nuclear medium occur. They may be expressed by an effective change of λ. We have taken λ = 0.026 [8] and pion mass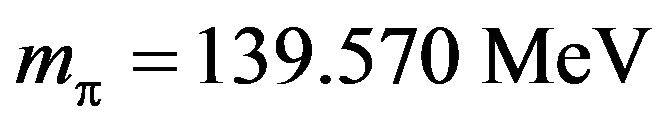 .
.
We take  to have
to have
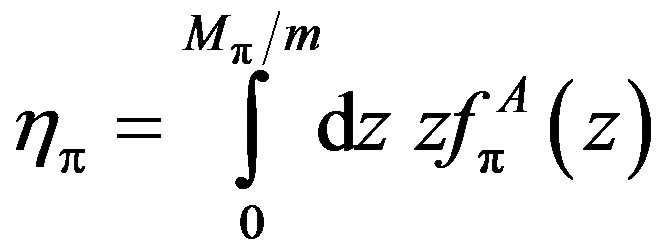 (4)
(4)
where  is the momentum fraction of pion. We have taken
is the momentum fraction of pion. We have taken 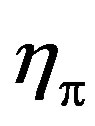 = 0.130 for 2H and
= 0.130 for 2H and 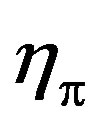 = 0.155 for 3He and 3H nuclei from [8], also
= 0.155 for 3He and 3H nuclei from [8], also 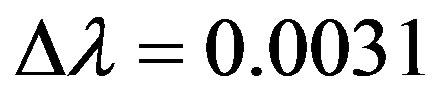 for 2H and
for 2H and  for 3He and 3H nuclei.
for 3He and 3H nuclei.
For pion structure function, we used follow parameterization [9,10]:
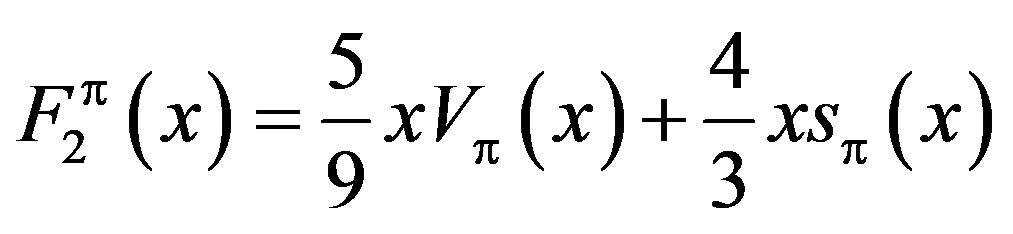 (5)
(5)
 (6)
(6)
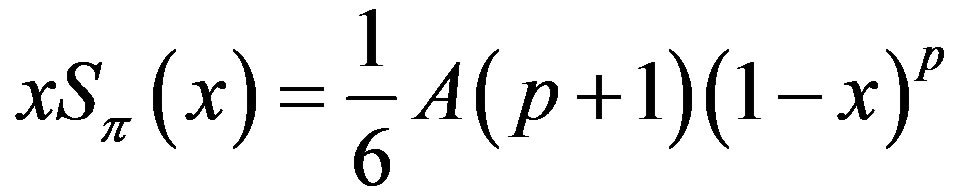 (7)
(7)
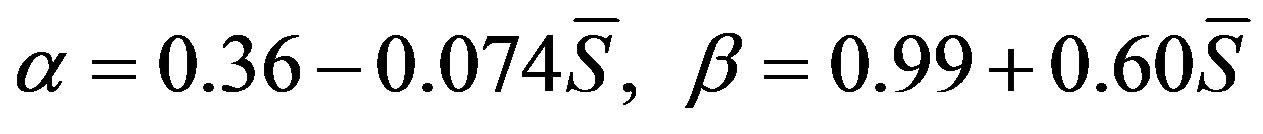 (8)
(8)
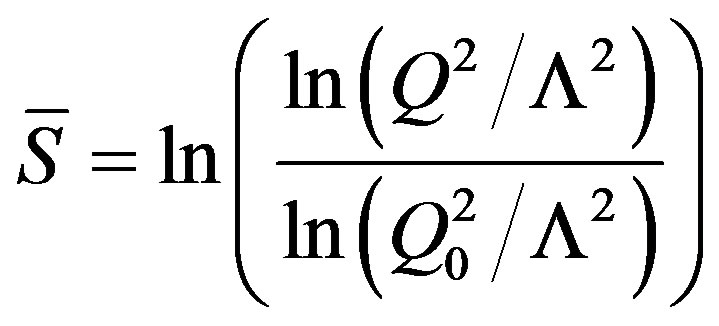 (9)
(9)
 (10)
(10)
In Figure 1, we plotted the momentum distribution of pions inside 2H, 3He and 3H nuclei.
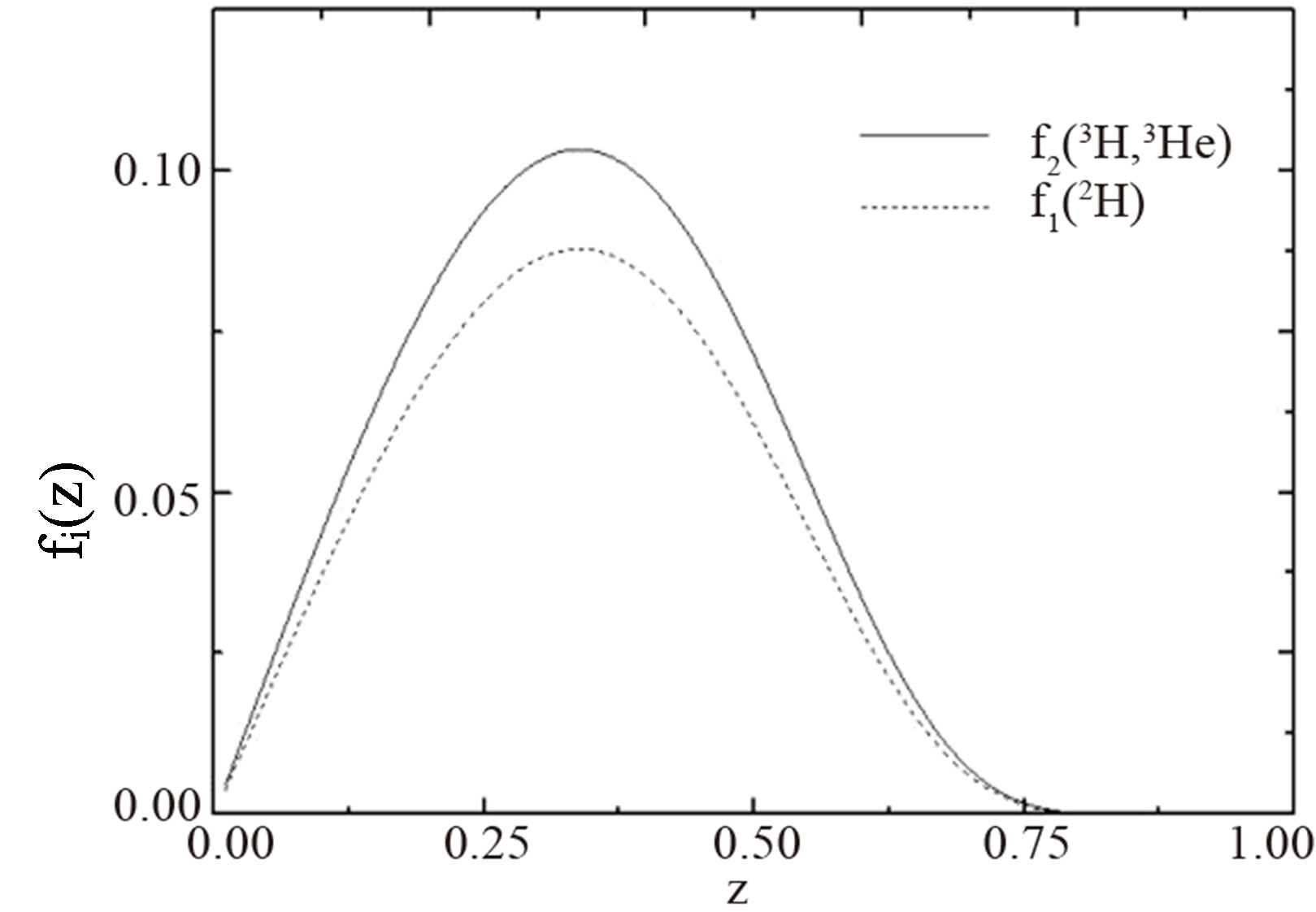
Figure 1. The momentum distribution of pions for 2H, i.e. i = 1 in figure, shown with dotted curve, 3He and 3H, i.e. i = 2 in figure, shown with full curve.
3. Calculating Differential Cross Section of Electron Scattering from Nucleus
The structure functions for charged lepton scattering from a nucleon are related to cross section by [11]:
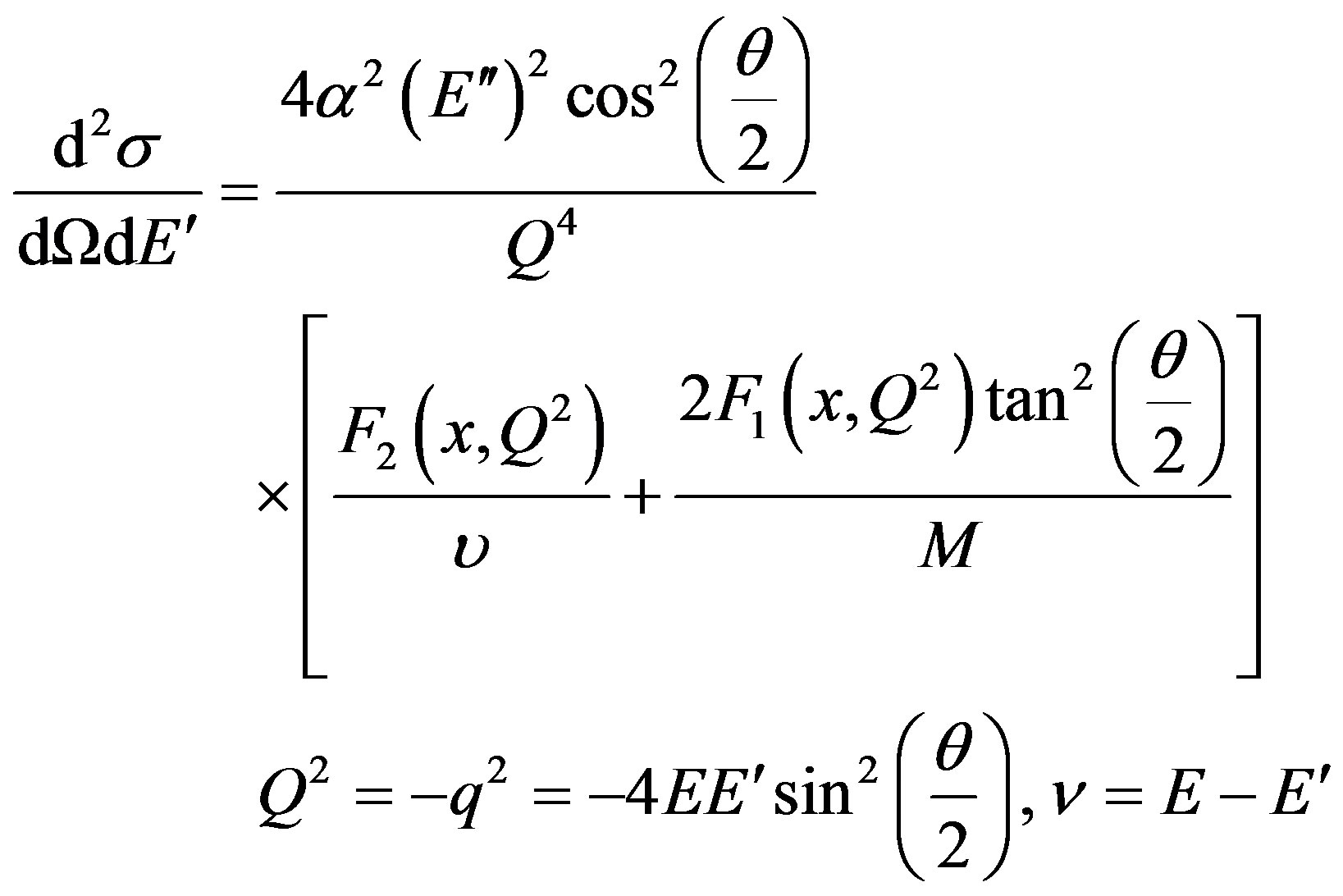 (11)
(11)
where
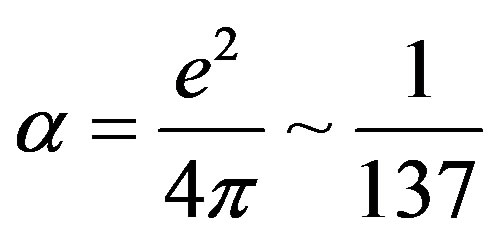
is the fine structure constant, four-momentum transfer squared is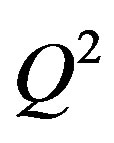 . Initial and scattered lepton energies are E and E', respectively. Energy of the virtual photon is
. Initial and scattered lepton energies are E and E', respectively. Energy of the virtual photon is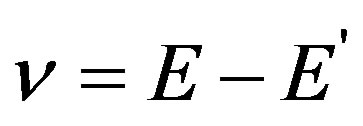 , and
, and
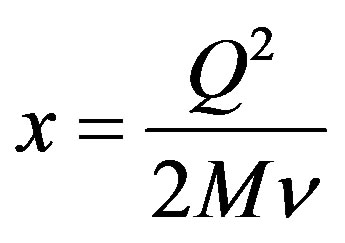
is Bjorken scaling variable. M is the nucleon rest mass. θ is the detected lepton scattering angle. F1 and F2 are the deep inelastic structure functions.
4. Results and Discussion
In Figures 2 and 3, nucleus structure functions for 3He
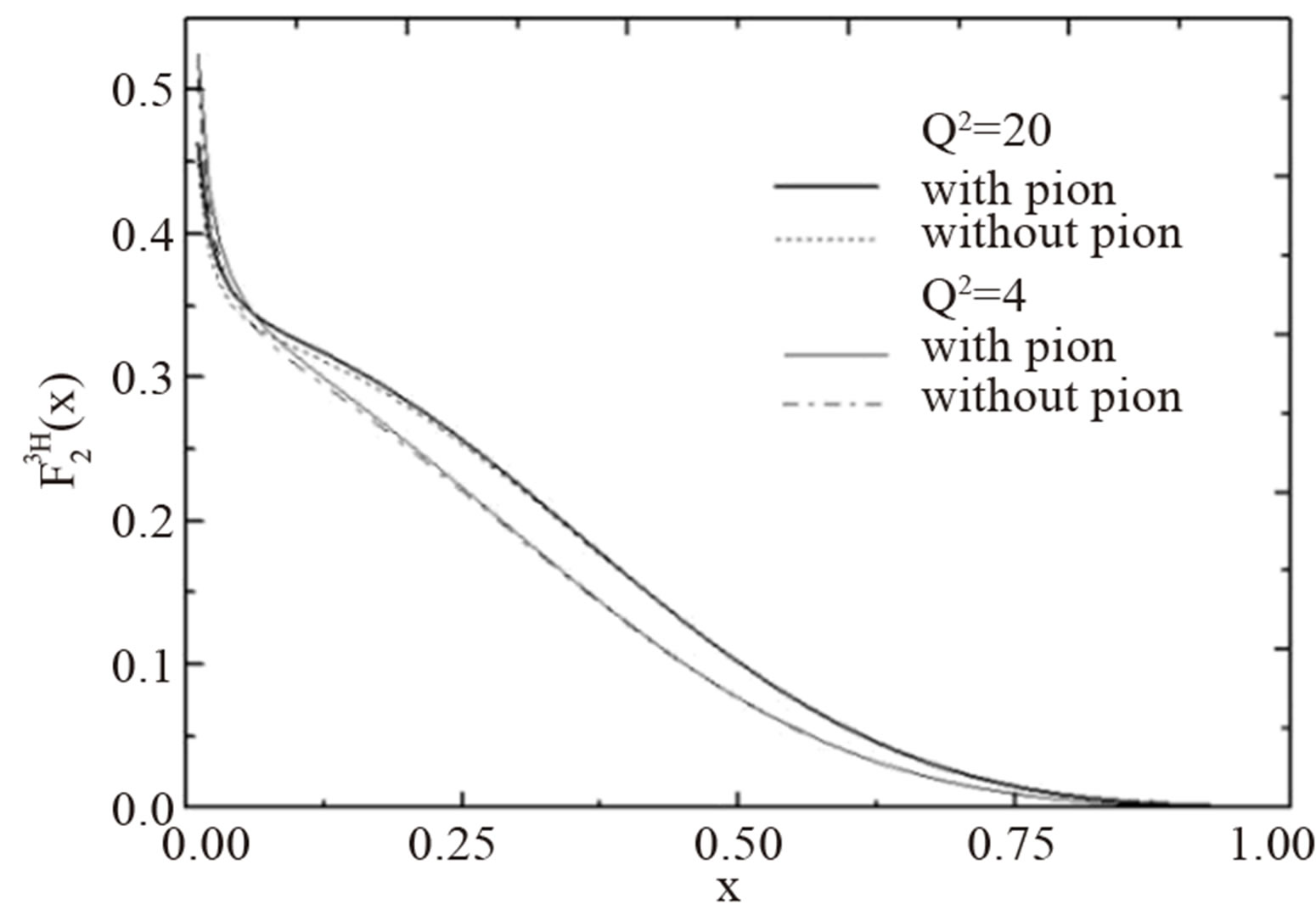
Figure 2. This figure shows 3H structure functions. The full curve is plotted for Q2 = 4 GeV2 with considering the Fermi motion, the binding energy, and the pionic contribution effect, the dotted curve is plotted with considering the Fermi motion, and binding energy effect. The full curve is plotted for Q2 = 20 GeV2 with considering the Fermi motion, the binding energy, and the pionic contribution effect, the line-dash is plotted with considering the Fermi motion, and the binding energy effect.
and 3H nuclei have been plotted by considering the Fermi motion, the binding energy and the pionic contribution. In this calculation we do not consider any difference between pionic cloud around the protons and neutrons and the contribution is equal 3H and 3He nuclear structure functions. This figure shows that the pionic contribution has maximum around x ≈ 0.2 that one expected.
In addition, the full curve in Figures 4 and 5 show differential cross sections of electron scattering from 3He and 3H nuclei with considering the Fermi motion, the binding energy and the pionic contribution. The dotted curves in Figures 4 and 5 show differential cross sections of electron scattering from 3He and 3H nuclei with considering only the Fermi motion and the binding energy effects. These figures show the pionic contribution
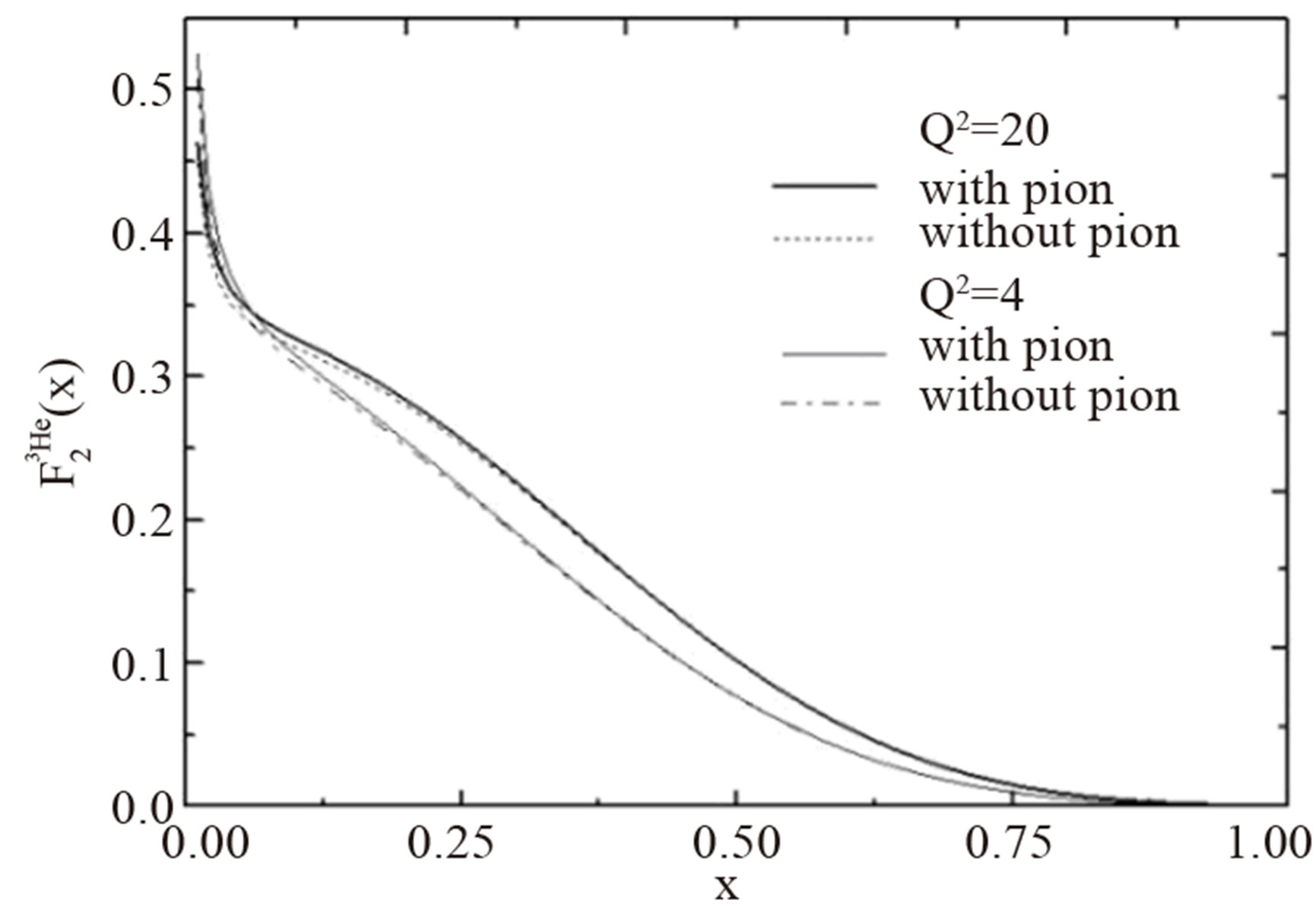
Figure 3. This figure shows 3He structure functions. The full curve is plotted for Q2 = 4 GeV2 with considering the Fermi motion, the binding energy, and the pionic contribution effect, the dotted curve is plotted with considering the Fermi motion, and binding energy effect. The full curve is plotted for Q2 = 20 GeV2 with considering the Fermi motion, the binding energy, and the pionic contribution effect, the line-dash is plotted with considering the Fermi motion, and the binding energy effect.
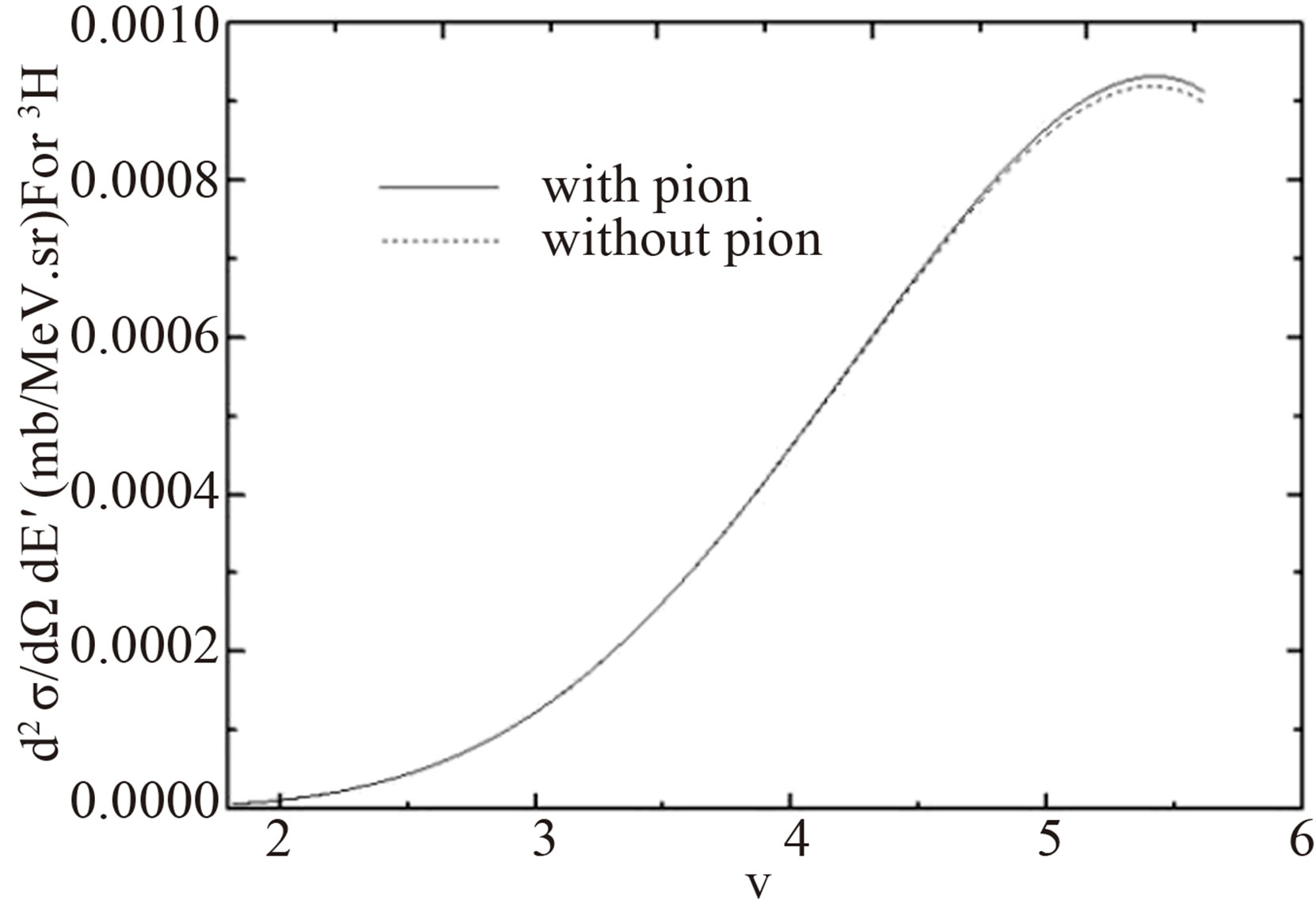
Figure 4. Differential cross section of electron scattering from 3H at θ = 8˚, Q2 = 4 GeV2, and E = 7.26 GeV. The full curve is plotted with considering the Fermi motion, the binding energy, and the pionic contribution. The dotted curve is plotted with considering only the Fermi motion and the binding energy.

Figure 5. Differential cross section of electron scattering from 3He at θ = 8˚, Q2 = 4 GeV2, and E = 7.26 GeV. The full curve is plotted with considering the Fermi motion, the binding energy, and the pionic contribution. The dotted curve is plotted with considering only the Fermi motion and the binding energy.
cloud improve cross section up to %1 or %2, which is perceptible in small x. In these figures pionic contribution increases when v goes up because pion cloud inside nuclei plays a role like sea quark inside nucleons.
REFERENCES
- G. Cattapan and L. Ferreira, “The Role of the Δ in Nuclear Physics,” Physics Report, Vol. 362, No. 5-6, 2002, pp. 303-407. doi:10.1016/S0370-1573(01)00093-X
- J. Ashman, B. Badelek, G. Baum, J. Beaufays, C. P. Bee, C. Benchouk, et al., “Measurement of the Ratios of Deep Inelastic Muon-Nucleus Cross Sections on Various Nuclei Compared to Deuterium,” Physics Letter B, Vol. 202, No. 4, 1988, pp. 603-610. doi:10.1016/0370-2693(88)91872-2
- P. Amaudruz, M. Arneodo, A. Arvidson, B. Badelek and G. Baum, et al., “Precision Measurement of the Structure Function Ratios F2He/F2D, F2C/F2D and F2Ca/F2D, Zeitschrift fur Physik C, Vol. 51, No. 3, 1991, pp. 387-393.
- The European Muon Collaboration, M. Arneodo, A. Arvidson, J. J. Aubert, B. Badelek, J. Beaufays, C. P. Bee, C. Benchouk, et al., “Measurements of the Nucleon Structure Function in the Range 0.002 < x < 0.17 and 00.2 < Q2 < 8 GeV2 in Deuterium, Carbon and Calcium,” Nuclear Physics B, Vol. 333, No. 1, 1990, pp. 1-47. doi:10.1016/0550-3213(90)90221-X
- M. Arneodo, “Nuclear Effects in Structure Functions,” Physics Report, Vol. 240, No. 5-6, 1990, pp. 301-393. doi:10.1016/0370-1573(94)90048-5
- S. V. Akulinichev, S. Shlomo, S. A. Kulagin and G. M. Vagradov, “Lepton-Nucleus Deep Inelastic Scattering,” Physical Review Letters, Vol. 55, No. 21, 1985, pp. 2239- 2241. doi:10.1103/PhysRevLett.55.2239
- M. Gluck, E. Reya and A. Vogt, “Dynamical Parton Distributions of Parton and Small-x Physics,” Zeitschrift fur Physik C, Vol. 67, No. 3, 1995, pp. 433-447. doi:10.1007/BF01624586
- T. Uchiyama and K. Saito, “European Muon Collaboration Effect in Deuteron and in Three-Body Nuclei,” Physical Review, C. Vol. 38, No. 5, 1988, pp. 2245-2250. doi:10.1103/PhysRevC.38.2245
- E. L. Berger and F. Coester, “Nuclear Effects in Deep- Inelastic Lepton Scattering,” Physical Review D, Vol. 32, No. 5, 1985, pp. 1071-1083. doi:10.1103/PhysRevD.32.1071
- K. Nakano, “Remarks on Pionic Constraints in the EMC Effect,” Journal of Physics G, Nuclear Part, Vol. 17, No. 11, 1991, pp. L201-L207.
- J. Gomez, R. G. Arnold, P. E. Bosted, C. C. Chang, A. T. Katramatou, G. G. Petratos, et al., “Measurement of the a Dependence of Deep-Inelastic Electron Scattering,” Physical Review D, Vol. 49, No. 9, 1994, pp. 4348-4372. doi:10.1103/PhysRevD.49.4348
NOTES
*Corresponding author.

