American Journal of Operations Research
Vol.06 No.04(2016), Article ID:68767,17 pages
10.4236/ajor.2016.64030
Aggregation of Priorities in Multi-Criteria Decision Analysis (MCDA): Connecting Decision Spaces in the Cognitive Space
Sajjad Zahir
Faculty of Management, University of Lethbridge, Lethbridge, Canada

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 June 2016; accepted 18 July 2016; published 21 July 2016
ABSTRACT
In Multi-Criteria Decision Analysis, the well-known weighted sum method for aggregating norma- lised relative priorities ignores the unit of scale that may vary across the criteria and thus causes rank reversals. A new aggregation rule that explicitly includes the norms of priority vectors is derived and shown as a remedy for it. An algorithmic procedure is presented to demonstrate how it can as well be used in the Analytic Hierarchy Process when norms of priority vectors are not readily available. Also, recursion relations connecting two decision spaces with added or deleted alternatives give an opportunity to extend the idea of connectivity to a new concept of cognitive space. Expanded analytic modelling embracing multiple decision spaces or scenarios may assist in detecting deficiencies in analytic models and also grasping the big picture in decision making.
Keywords:
Aggregation, Normalization, Decision Space, Cognitive Space, Analytic Hierarchy Process, Scenario

1. Introduction
In Multi-Criteria Decision Analysis (MCDA), often a complex decision problem is decomposed into a hierarchy of criteria, sub-criteria and alternatives. For such decomposition, one assumes that the decision about alternati- ves in respect of one criterion (or sub-criterion) can be made independent of decisions made in respect of other criteria (or sub-criteria). It also becomes easier for a decision maker (DM) to understand and analyze the decision hierarchy in small segments at a time. Finally, results (i.e., criteria and sub-criteria weights and alternative priorities) from different segments are aggregated. Integrated values for the decision alternatives can be presented as aggregate scores, normalised relative priorities or ordinal ranks. In this paper, we consider a simple three level hierarchy without any loss of generality. The top level represents the overall goal of the decision. The second level represents the criteria, and the third level is for a list of alternatives. The criteria are characterised by weights that may sum to one. The priorities of the alternatives under each criterion may be expressed as un-normalised preference scores or relative priorities that are normalised such that they sum to one. The preference scores or the relative priorities are often derived from a Multi-Criteria Decision Model (MCDM). Finally, the criteria weights and alternative priorities are aggregated to generate an overall rating for alternatives.
A commonly used aggregation procedure, introduced in the Multi-Attribute Value/Utility Theory (MAVT/ MAUT), is the weighted sum method (see [1] for a brief overview and references therein). Preference scores or value scores are obtained for each alternative in reference to all attributes or criteria. Then, the weighted sum aggregation can be done in two ways. a) One can obtain the weighted sum of the preference scores (i.e., before normalization) across the criteria for each alternative and then normalize them to obtain the final relative priorities. b) One can just get the weighted sum of the already normalised relative priorities of the alternatives across the criteria to get the final priorities that may not require further normalization. The final results obtained from these two approaches are not the same. Not only so, the ones obtained by method a) are free from the rank reversal problem. The ones obtained by method b) may be affected by the reversal of ranks if another alternative is added or an existing one is deleted from the decision space. Many other types of MCDM techniques and associated aggregation procedures are discussed in the MCDA literature (for example, see [2] and references therein). However, in this paper we will focus on the additive aggregation approach such as the weighted sum method (WSM) [3] .
In any MCDM technique, since method b) may cause unwanted rank reversals, it is justified to question the validity of the aggregate values derived using this technique. This observation brings the Analytic Hierarchy Process (AHP) [4] [5] , a familiar MCDM, into focus. It initiated vigorous discussions about the rank reversal problem (see [6] for a comprehensive review and references) during the last few decades. The AHP provides normalised relative priorities for alternatives from pairwise comparison matrices under each criterion and uses method b) for aggregation across criteria. However, the unit of scale (which essentially is the norm of the vector representing the priorities) used in normalising the relative priorities of alternatives for different criteria may be different. Aggregation method b) ignores this fact causing unwanted rank reversals. Therefore, Zahir [7] suggested a modified weighted aggregation formula (based on intuitive reasoning) that incorporated norms of the priority vectors. This procedure takes into account the variation of the unit of scale across the criteria. Zahir [7] used recursion rules and several numerical examples to illustrate the method for computing the correct aggregate relative priorities that are free from rank reversals. In contrast, the well-known simple weighted sum formula used with normalised priorities perhaps gives flawed results. In this paper, we derive the proposed aggregation rule from a rigorous and generalised mathematical approach [8] making the proposed aggregation rule for MCDA more significant. We discuss, with numerical examples, how this aggregation rule can be used albeit utilising additional information in methodologies that generate only normalised alternative priorities for each criterion (e.g., the AHP).
In addition, based on recursion relations that link two decision spaces having an added or deleted alternative, we introduce the concept of cognitive space spanning multiple decision spaces or scenarios. We present arguments for expanding the usual modelling experiences beyond a particular decision space into the cognitive space. Expanded modelling will help us detect shortcomings if any, of models developed on a particular decision space. In Section 2, we outline the new contributions of this paper. We provide a generalised derivation of a modified aggregation rule, further discuss recursion relations and overview the meaning of weights in this context. Section 3 and Section 4 demonstrate the use the new aggregation rule in the AHP with numerical examples. Section 5 delineates the concept of expanded analytical modelling in cognitive space and conclusions are made in Section 6.
2. Representation of the Generalised Decision Space and Formulation of the Modified Aggregation Rule
In this section, starting from a generalised multi-criteria decision space, a modified aggregation rule is derived and contrasted with the familiar WSM. Calculations involve combining measurements from two different spaces (i.e., criteria space and alternative space), each having different units of scale and may have different dimensions, too. However, no mathematical derivation for the WSM which represents a complex measurement procedure is available in the MCDA literature. Perhaps, the formula was introduced as a simple extension of the expected value formula with the normalised weights replacing probabilities. The earlier work [7] also started with the WSM and modified it to incorporate norms of the priority vectors. The new contributions in this paper include a formal mathematical derivation of the modified weighted sum method showing how the norms of priority vectors naturally appear in formal mathematics spanning the criteria and alternative spaces. The other contribution is the discussion of cognitive space that connects multiple decision spaces, each represented by a set of criteria and alternatives. This approach helps us to project the rank reversal problem as a cognitive issue in the context of an expanded analytic modelling framework. As an alternative is added or deleted, the logical connections between decision spaces are also analysed later in this section in terms of the recursion rules. In the end, we discuss the impact of normalisation of criteria weights whose meanings are further reviewed in reference to earlier MCDA research.
2.1. Modified Weighted Sum Aggregation Rule from the Generalised Decision Space
We consider a decision space with n alternatives judged with respect to m criteria as represented by the hierarchy diagram in Figure 1. The criteria and alternatives constitute two distinct spaces, S(C) and S(A) respectively. S(C) is m dimensional and S(A) is n dimensional vector spaces spanned by a set of orthonormal basis vectors αi, (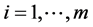 ) and βj, (
) and βj, (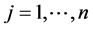 ) respectively where the basis vectors are just column vectors of dimension m and n respectively,
) respectively where the basis vectors are just column vectors of dimension m and n respectively,
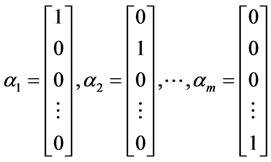
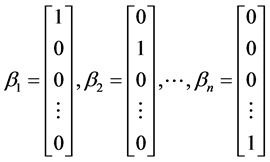
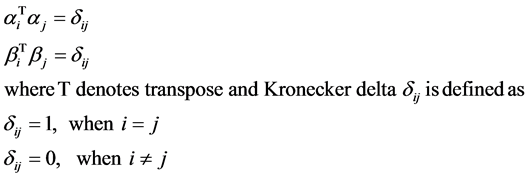 (1)
(1)
Let us assume that the criteria weights (implying the relative importance of the criterion) can be obtained from any available technique. We develop formulations of this section independent of any particular model (e.g.,
Figure 1. Decision hierarchy.
AHP). We represent the weights by a vector w and for the sake of convenience we assume that the weights are normalised such that they sum to one. The rest of the discussions in this section will not change even if the weights are not normalised (in that case weights will be a constant multiple of the normalised ones). So, the weight vector w is,
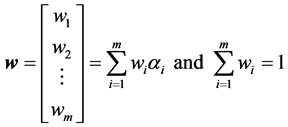 (2)
(2)
Similarly, with respect to ith criterion, let the priority vector for n alternatives be
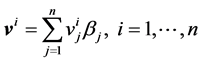 (3)
(3)
The priority vectors vi can be obtained in various ways subject to a decision model. For example, it can represent a set of scores as obtained from a decision maker’s mental model or it can be obtained from the pairwise comparison matrix (Pi) as in the AHP. If one employs the eigenvector method in the AHP, then it can be just an eigenvector (not necessarily normalised) derived from the eigenvalue equation,
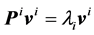 (4)
(4)
Other methods such as minimization of logarithmic least-square approach have been discussed in the AHP literature as well (see [9] ). However, our discussion of aggregation is not restricted to any particular method of eliciting the priority vector from decision maker’s preferences. In a generic form, we can represent this decision-making exercise by a generic operation (GO) in Figure 2.
If ui is the corresponding normalised priority vector, then
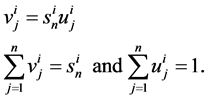 (5)
(5)
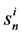 is the norm of the unnormalised priority vector with n alternatives with respect to the ith criterion. In the scoring method,
is the norm of the unnormalised priority vector with n alternatives with respect to the ith criterion. In the scoring method, 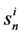 is known, but in the AHP it is unknown.
is known, but in the AHP it is unknown.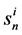 , the norm of n-dimensional priority vector sets the unit of scale for the normalised priority vector uij and can vary for different criteria. Therefore, the correct aggregation rule should incorporate
, the norm of n-dimensional priority vector sets the unit of scale for the normalised priority vector uij and can vary for different criteria. Therefore, the correct aggregation rule should incorporate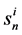 .
.
The combined decision space D is a direct product of the criteria space and the alternative space, i.e.,
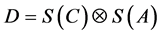
Thus, the priority state y is derived from a direct product of w and vi s so that it preserves the hierarchic structure of Figure 1. We compute the sum of the direct products of the orthogonal components of w in the criteria space with the corresponding priority vectors under each criterion. That is,

Figure 2. Generating priority vector from DM’s preference inputs.
Please note that the column vectors αi s are defined in m dimensional criteria space and vi s are defined in the n-dimensional alternative space.
It is worth pointing out that, in general, there are arbitrary constants multiplying each term in the expansion of Equation (6). For convenience, we absorbed them in vi s and thus in the corresponding norms
Now expanding vi s in terms of the basis vectors βj given in Equation (3), we finally have,

We project out the intensity of priority corresponding to the pth state of the criteria space and the qth basis state of the alternative space by multiplying on the left by 


In additive models, we sum over all criteria to obtain the aggregate priority Rq of alternative q,

Now, using the relation between the unnormalised local priority 


The normalised aggregate priority rq (i.e.,

The above expression should be compared with the traditional weighted sum formula called Simple Aggregation Rule (SAR),

The MAR was proposed as the correct aggregation procedure for obtaining overall priorities in [7] . It is worth pointing out at this stage that if the weight vector was not normalised (i.e., if in Equation (6) we used un-norma- lised weights Wp), we would have

It is straightforward to check that the expression of the normalised aggregate priority rq in Equation (11) would remain the same confirming that we did not sacrifice any generality by considering a normalised weight vector at the very beginning in Equation (6).
It should be further noted that the proposed aggregation rule (MAR) becomes identical with the familiar weighted sum rule (SAR) only when norms of all priority vectors are equal (i.e.,
The above result is independent of decision models that one would use to derive values for the alternative priority vectors. For example, Saaty [4] [5] developed an ingenious mechanism based on reciprocal pairwise comparison matrices and an eigenvalue equation for deriving the normalised local priorities in the AHP. Values for 
2.2. Recursion Rules
Two recursion rules used in [7] for the rank reversal analysis are re-stated below (can be derived easily following the same procedure with a slight change in notations).
1) When a new alternative (i.e., the (n + 1)th alternative) is added to the decision space (the primed items refer to the corresponding quantities in the new decision space with n + 1 alternatives), in a fully consistent case,


2) When an existing alternative (i.e., the nth alternative) is deleted from the decision space (the primed items refer to the corresponding quantities in the new decision space with n − 1 alternatives), in a fully consistent case,


Using the MAR, it can be proved [7] that ratio of two aggregate priorities for alternatives is preserved when a new alternative is added or an existing one is deleted (see Appendix A).
2.3. Meaning of Criteria Weights in the Modified Aggregation Rule
In MCDA research, it has been noted [10] that the most widely used and the simplest aggregation method is the weighted sum method (WSM). Considering n alternatives and m criteria, the aggregate preference Pi of alternative Ai (
where, W j is the weight of the jth criteria. Here, 


the normalisation of weights does not affect the MAR that is being proposed here as the correct aggregation method as it prevents rank reversals. But, rank reversals may occur in the SAR where the 
Here, in this research, we may be tempted to redefine the criteria weights as follows absorbing the norms (i.e., additional information) of the priority vectors:

But, because of the recursion relations in Equation (14) and Equation (16), the new weights



3. Using the Proposed Aggregation Rule: Special Case of the AHP
In the AHP, we can determine weights wp and the local normalised alternative priorities 






In the following formulations, we will assume that there are n alternatives, so we will suppress the index n and will restore it only in the final results. Estimating values for 

In Step 3.1 of Text Box 1, m estimates for the preference scores for alternative 1 is required. In MAVT, such values are obtained from value functions. However, m estimates for the preference scores for alternative 1can be estimated assuming a Beta distribution as a possible choice if we want to deal with the underlying uncertainty stochastically.
Let a decision maker estimates the norm (n = 1), following a Beta distribution, as follows:
bp = high end estimate for


Then, then 
Average score for
Zahir [7] also suggested a technology-based visual interface for estimating the preference scores 
4. Discussion of Results and Future Research
In the preceding sections, we observed that as we move from one decision space to another (obtained by adding or deleting an alternative), the decision model can generate meaningful results only if the aggregation rule is the correct one. This “correctness” is based on our reasoning, i.e., ranks should not reverse when they are not expected to. We illustrated with numerical examples how the MAR supported our correct expectations. Deficiencies of the SAR were detected only when logical reasoning could not be satisfied by calculated results as an alternative was added to or deleted from a decision model. This observation emphasises the need for testing the validity of analytic modelling over an expanded model space. In the AHP (or MAVT using the SAR), if the early developers considered results of two decision spaces (obtained by adding and subtracting alternatives), they would have identified the deficiency of the SAR. An improved aggregation rule that incorporated the unit of scale would have been used in the normalisation of alternatives such as the MAR being discussed in this paper. Such an expanded “big picture” framework is outlined below.
4.1. Cognitive Space and Decision Space: Framework for Avoiding Modelling Deficiencies
In the context of an MCDM, decision making can be discussed in terms of the decision space that is cha- racterised by the number of alternatives and criteria. Alternatives and criteria have numerical values or subjective values (derived from a decision maker’s cognitive process and its interaction with the external world) in a quantitative or a qualitative decision model respectively. However, in this paper, since we are dealing with quantitative decision modelling we assume that we can assign numerical values to our judgements. In general, there can be a large number of choices for the number of alternatives and criteria making a decision problem complex. Often the problem is represented by a model that is nothing but an abstraction of the reality. However, the analysing capability of humans as rational beings, even with technological assistance, is limited and thus we are inclined to “satisfice” by setting a boundary to the decision spaces. The boundary can change as we acquire more knowledge about the problem or are subject to different external influences. This effect can be understood in light of Simon’s bounded rationality [14] .
As more alternatives (or criteria) are added or some are deleted, the decision space expands or contracts creating a new decision space for the underlying decision model. The set of related decision spaces collectively is the cognitive space of the decision problem, and we try to link them through reasoning and understanding. Each decision space is also a cognitive sub-space where model formulations are defined in terms of logic, reasoning and facts. Often, the links among decision spaces are done in human minds and are left out of the decision models and thus each model is treated independently in its own decision space. But, together they are discussed by researchers in their cognitive domain via reasoning processes. Our memory is a repository of information and it plays a significant role in linking the analyses of the decision spaces via reasoning. Thus, it helps us connect scenarios in decision spaces logically to the satisfaction of our rational minds.
We can think of a Gedanken experiment in reference to the example in Section 4. We keep the inputs same as in Section 4. Suppose a DM computes the relative priorities using the SAR for three alternatives. And then she takes a nap and wakes up when she has no memory of the priorities derived before the nap. Now, she computes the relative priorities using the SAR again for four alternatives and obtains new results. Since she has no memory of the results she obtained before the nap, does it matter even if the ranks now are reversed? Most probably it does not. However, in reality we have memory, and our cognitive process finds reasoning to link findings and results from related decision spaces. The links of reasoning connecting the results from one decision space to another as they reside in our memory are not incorporated in the decision models or, may be, models are deficient in part. We reason in our minds. Sometimes, we also fail to satisfy our reasoning and then we raise the question about the validity of a decision model as it stands. It may be due to a flaw in parts of the model and therefore it needs to be corrected. Another approach that has not been widely pursued in practice may be to extend the decision model across the cognitive space that would also model the reasoning links among the decision spaces. That would also help us find a solution to an apparent imperfection in a decision model.
As it has been discussed earlier, when a new alternative is added or an existing alternative is deleted (i.e., moving from one decision space to another in the cognitive space of the decision problem (see Figure 3) by expanding or contracting the decision space), the ranks may be reversed in the SAR-based AHP. We face a problem in our reasoning as we find it difficult to understand the reversal of ranks when such a reversal of ranks is not supposed to happen. In the MAR, associated recursion rules demonstrate how the units of scale (set by the norm of the preference vectors) change as we make a transition from one decision space to another (i.e., from DS-i to DS-j in Figure 3). The MAR takes this effect into the formulation and thus preserves ranks of existing alternatives when they are expected to preserve. The MAR models decision spaces DS-i and DS-j and also represents cognitive link CLij representing the reasoning that links DS-i and DS-j in the cognitive space. CLij represents the recursion rules that asserts that norms (setting the scale of normalisation) of priority vectors change as an alternative is added or deleted, and the MAR incorporates this assertion preserving ranks when it should. The SAR is deficient as it does not incorporate the scale of normalisation and hence produces unwanted rank reversals.
Here, we may attempt to relate decision spaces to a simplified form of scenarios as a parallel concept. The idea of scenario has been discussed for over 40 years (see [15] for some early references) in the context of strategic decision making in many areas of applications including the MCDA (see [16] and [17] and references therein). Huss [15] called a scenario “a narrative description of a consistent set of factors that define in a probabilistic sense alternative sets of future business conditions” and discussed its application to forecasting. The
Figure 3. Decision spaces in cognitive space.
concept of a scenario is still an evolving one but it is clear that each scenario has a context. Tversky and Kahnemann [18] realised difficulties in developing scenarios and stated “it is exceedingly difficult for the human mind to apprehend sequences of variations of several interacting factors. We suggest that in evaluating the probability of complex events, only the simplest and most likely scenarios are likely to be considered.” In this paper, we keep our discussions about scenarios limited to the MCDA.
We have stressed the need for linking decision spaces so as to test the validity of mathematical models. The analysis presented in the preceding sections lead us to the correct aggregation rule called the MAR. The simplified version of the scenario that we adopt is defined by a set of alternatives and criteria and preferences assigned to them by a DM, who sets the context of the scenario. The context emerges as the DM assigns to alternatives and criteria subjective and objective judgements that are influenced by his/her value system and sense of uncertainty. Mathematically speaking, in a modelling environment the context is created by a set of variables, operators and constraints formulated as mathematical expressions. Thus, as we navigate from one decision space to another, some of the things that can happen are,
Parameter values change.
New parameters enter.
Old parameters may drop out.
Expressions are re-evaluated (e.g., the recursion relations in preceding sections).
New constraints may emerge.
And so on.
If we have a valid model, its predictions would satisfactorily track our cognitive expectations not only in a particular decision space but also as navigate to others. Gomes and Costa [19] concluded that the traditional approach of multi-criteria decision-making factoring in a single vision of scenarios might result in less than robust suggestions for decision-makers. In their research, they considered multiple scenarios where the criteria weights were evaluated independently for each scenario keeping number of alternatives unchanged to obtain a robust set of [17] explored possibilities of integrating MCDA with scenario analysis and illustrated the concept with an agricultural policy planning example in a developing country. In this example, they kept the number of alternatives and criteria across scenarios unchanged but preferences were assigned in the context of the scenarios. Ram et al. [16] considered a case where the number of alternatives and criteria were unchanged but their preferences were varied across scenarios for improved evaluation of strategic options. In our case, we got the correct aggregation rule (MAR) that avoided rank reversals as the number of criteria and their weights were unchanged but another alternative was added or deleted. While others have extended the use of scenario planning and MCDA for improved strategic decisions, we promote a framework for improved decision modelling in terms of a parallel concept of decision spaces (i.e., simplified scenarios) embedded in a cognitive space.
4.2. Future Research
While we discussed the multi-criteria decision problem in light decision spaces, we can extend the concept to scenarios applicable to other areas of decision sciences. In management science and operational research, we make models for inventory/supply chain, resource allocation, financial market analysis, portfolio management, etc. based on a particular scenario (analogous to a decision space). Then, we change models as scenarios change (often probabilities are assigned to each scenario in scenario analysis). We try to understand the varying results in our reasoning as we connect scenarios utilising our memory and cognitive strength. It may be possible to include intra-scenario reasoning by having cognitive links in the models spanning more than one scenario. If the models cannot explain results from two scenarios, that can be attributed to a deficient component or weakness of the model itself and thus will call for improvement in the model. We can also try to understand the significance of such integrated multi-scenario decision modelling in light of system thinking [20] . An inter-related reasoning embedded in the expanded analytics is expected to help understand “the whole” for better decision making. The multiple decision spaces or scenarios will be linked by a network in the cognitive space with an objective to assist in forming a decision representing a “big picture”.
5. Conclusion
We identified the deficiency of the traditional weighted sum aggregation rule used in the AHP and possibly in the MAVT with the prior normalisation as the cause for rank reversals and proposed a modified aggregation rule as a remedy. Utilising recursion rules, we analyzed the additive aggregation process in light of the new aggregation rule. We also suggested ways how it could be used with the AHP or MAVT with prior local normalisation. The ideas are illustrated with numerical examples. Also, we discussed possibilities for extending usual modelling techniques developed in the context of a particular decision space or scenario to an expanded form in the cognitive space. Concepts of satisficing and bounded rationality were invoked for managing such expansions. Testing the validity of mathematical models in decision sciences, operations management and possibly economics may need the support of a “big picture” beyond a single scenario.
Cite this paper
Sajjad Zahir, (2016) Aggregation of Priorities in Multi-Criteria Decision Analysis (MCDA): Connecting Decision Spaces in the Cognitive Space. American Journal of Operations Research,06,317-333. doi: 10.4236/ajor.2016.64030
References
- 1. Belton, V. and Stewart, T.J. (2002) Multiple Criteria Decision Analysis: An Integrated Approach. Springer-Science + Business Media, B.V., Berlin, Heidelberg.
- 2. Bouyssou, D., Marchant, T., Pirlot, M., Tsoukias, A. and Vincke, P. (2006) Evaluation and Decision Models With Multiple Criteria. Springer-Science + Business Media Inc., New York.
- 3. Fishburn, P.C. (1967) Additive Utilities with Incomplete Product Set: Applications to Priorities and Assignments. ORSA Publication, Baltimore.
- 4. Saaty, T.L. (1980) The Analytic Hierarchy Process. McGraw-Hill, New York.
- 5. Saaty, T.L. (1995) Decision Making for Leaders. RWS Publications, Pittsburgh.
- 6. Maleki, H. and Zahir, S. (2013) A Comprehensive Literature Review of the Rank Reversal Phenomenon in the Analytic Hierarchy Process. Journal of Multi-Criteria Decision Analysis, 20, 141-155.
http://dx.doi.org/10.1002/mcda.1479 - 7. Zahir, S. (2009) Normalisation and Rank Reversals in the Additive Analytic Hierarchy Process: A New Analysis. International Journal of Operational Research, 4, 446-467.
http://dx.doi.org/10.1504/IJOR.2009.023538 - 8. Zahir, S. (1999) Geometry of Decision Making and the Vector Space Formulation of the Analytic Hierarchy Process (AHP). European Journal of Operational Research, 112, 373-396.
http://dx.doi.org/10.1016/S0377-2217(98)00020-4 - 9. Choo, E.W. and Wedley, W.C. (2004) A Common Framework for Deriving Preference Values from Pairwise Comparison Matrices. Computers and Operations Research, 3, 893-908.
http://dx.doi.org/10.1016/S0305-0548(03)00042-X - 10. Triantaphyllou, E. and Sanchez, A. (1997) A Sensitivity Analysis Approach for Some Deterministic Multi-Criteria Decision-Making Methods. Decision Sciences, 28, 151-194.
http://dx.doi.org/10.1111/j.1540-5915.1997.tb01306.x - 11. Schoner, B. and Wedley, W.C. (1989) Ambiguous Criteria Weights in AHP: Consequences and Solutions. Decision Sciences, 20, 462-475.
http://dx.doi.org/10.1111/j.1540-5915.1989.tb01561.x - 12. Choo, E.W., Schoner, B. and Wedley, W.C. (1999) Interpretation of Criteria Weights in Multicriteria Decision Making. Computers & Industrial Engineering, 37, 527-541.
http://dx.doi.org/10.1016/S0360-8352(00)00019-X - 13. Zahir, S. (2006) Eliciting Ratio Preferences for the Analytic Hierarchy Process with Visual Interfaces: A New Mode of Preference Measurement. International Journal of Information Technology and Decision Making, 5, 245-262.
http://dx.doi.org/10.1142/S0219622006001939 - 14. Simon, H.A. (1979) Models of Thought. Yale University Press, New Haven.
- 15. Huss, W.R. (1988) A Move toward Scenario Analysis. International Journal of Forecasting, 4, 377-388.
http://dx.doi.org/10.1016/0169-2070(88)90105-7 - 16. Ram, C., Montibeller, G. and Morton, A. (2011) Extending the Use of Scenario Planning and MCDA for the Evaluation of Strategic Options. Journal of the Operational Research Society, 62, 817-829.
http://dx.doi.org/10.1057/jors.2010.90 - 17. Stewart, T.J., French, S. and Rios, J. (2013) Integrating Multicriteria Decision Analysis and Scenario Planning—Review and Extension. Omega, 41, 679-688.
http://dx.doi.org/10.1016/j.omega.2012.09.003 - 18. Tversky, A. and Kahneman, D. (1983) Extensional vs. Intuitive Reasoning: The Conjunction Fallacy in Probability Judgment. Psychological Review, 90, 293-315.
http://dx.doi.org/10.1037/0033-295X.90.4.293 - 19. Gomes, C.F.S. and Costa, H.G. (2014) Using Prospective Vision and Multi-Criteria Decision Analysis with Scenario Planning. In: Simpósio Brasileiro de Pesquisa Operacional XLVI, 2014, Salvador. Anais do SBPO 2014. Iltc, Niteroi, 489-500.
http://www.researchgate.net/profile/Carlos_Gomes5/publication/265851236_Using_Prospective_Vision_and_Multi-Criteria_Decision_Analysis_with_Scenario_Planning/links/541f350e0cf203f155c24cc7.pdf - 20. Senge, P.M., Kleiner, A., Roberts, C., Ross, R.B. and Smith, B.J. (1994) The Fifth Discipline Fieldbook. Currency and Doubleday, New York.
- 21. Belton, V. and Gear, A.E. (1983) On a Shortcoming of Saaty’s Method of Analytic Hierarchies. Omega, 11, 228-230.
http://dx.doi.org/10.1016/0305-0483(83)90047-6 - 22. Zahir, S. and Al-Mahmud, Z. (2009) Experimenting with the Proposed New Aggregation Rule for the Additive Analytic Hierarchy Process: Consistency vs. Rank Reversal. Proceedings of the Annual Conference of the Administrative Sciences Association of Canada (ASAC), Niagra Falls, 6-9 June 2009, 1-12.
http://ojs.acadiau.ca/index.php/ASAC/article/viewFile/500/409
Appendix A
The aggregation rule that we derived in the text (also see [7] ) preserves rank of any two alternatives when a new alternative is added or an existing one is deleted. This is independent of the model used to derive normalised local priorities of alternatives under each criterion. We give the mathematical proof below following previous work [7] .
1) An alternative is added
Let 




From Equation (14), we have

However, in a fully consistent case, we have from Equation (5) and Equation (14),

So, finally we get from Equation (A2),

2) An existing alternative is deleted
Let 




From Equation (15) and Equation (A5), we have

However, in a fully consistent case, we have from eqs (5) and Equation (15),

So, finally we get from Equation (A6),

Appendix B
A Numerical Example for Using the MAR
For the sake of illustration, in this section we demonstrate the use of the algorithm given in Section 3 for computing aggregate relative priorities in the AHP using a numerical example. It is a two-level hierarchy having three criteria and three alternatives. It is the same example as the one employed in [21] . Below it is presented in a tabular form. It is the same example as the one employed in [21] and is presented below in Table 1.
Table 1. Preference scores for three alternatives with three criteria.
With absolute scores known, we can construct pairwise comparison matrices under each criterion and compute normalised local relative priorities as in Table 2 (since we have the absolute scores, the relative priorities could be computed directly as well).
Table 2. Normalised relative priorities.
Aggregate relative priorities using the SAR and the MAR (Equation (12) and Equation (11) respectively) are given in Table 3.
Table 3. Aggregate relative priorities using the SAR and the MAR.
In Table 3, numbers in the SAR and the MAR columns are not the same as noted earlier. In the AHP, norms are not known and thus using the MAR is problematic. Algorithm of Text Box 1 utilizes additional information needed as shown in the shaded block in Table 1. The minimum set of information required is shown in the shaded block of Table 4,
Table 4. Initial inputs needed to implement the algorithm in Text Box 1.
We add another alternative and the PCMs are given in Table 5.
Table 5. Pairwise comparison matrices for two alternatives.
The normalised relative priorities obtained from the PCMs using the eigenvalue method are calculated in Table 6.
Table 6. Local relative priorities obtained from PCMs in Table 5 and using eigenvalue method.
Using the norms in the bottom row of Table 4 and the recursion relation Equation (14), we get new norms in Table 7.
Table 7. Calculated norms for two-alternative priority vectors using the recursion relation.
Next we add a third alternative and the PCMs are given in Table 8.
Table 8. Pairwise comparison matrices for three alternatives.
The normalised local relative priorities derived from the PCMs using the eigenvalue method are presented below in Table 9.
Table 9. Local normalised relative priorities obtained from PCMs in Table 8 and using eigenvalue method.
Using the numbers in Table 7, Table 9 and the recursion relation of Equation (14), we have the new norms for three alternatives in Table 10.
Table 10. Norms for three-alternative priority vectors using the recursion relation.
Finally, the aggregate relative priorities computed using the MAR are (compare with Table 3) given in Table 11.
Table 11. Aggregate relative priorities using the MAR.
The above numerical exercise demonstrates how the MAR can be used in the AHP as explained in the algorithm of Text Box 1. We performed extensive numerical analysis and confirmed that the final results are independent of the relative order of the alternatives. Rank reversals are avoided using the MAR as long as the comparisons are consistent. In the presence of inconsistency, rank reversal can happen even with the MAR; but that is acceptable as imperfections in judgments. We performed simulation of the algorithm with random presence of inconsistencies and observed rank reversals varying with amount of inconsistencies (see [22] for details). If we
have a simple hierarchy with one level of m criteria and n alternatives, we need m additional inputs for



However, the procedure involves extra computational steps but generates correct aggregate relative priorities for the alternatives. To substantiate this claim, let us add another alternative (D) to the example above. The PCMs are given in Table 12.
Table 12. Pairwise comparison matrices for four alternatives.
The normalised relative priorities obtained by eigenvalue method are calculated in Table 13.
Table 13. Local normalised relative priorities obtained from PCMs in Table 12 and using eigenvalue method.
Using the numbers in Table 10 and Table 13 and the recursion relation Equation (14), we present the computed norms for three alternatives Table 14.
Table 14. Norms for four alternative priority vectors using the recursion relation.
The aggregate relative priorities are (using both the MAR and the SAR) presented in Table 15.
Table 15. Aggregate relative priorities using the MAR and the SAR.
The important point to note is that the ranks of A and B are reversed by the SAR but are preserved by the MAR! Therefore, if we use the MAR that was derived in Section 3, we can avoid the rank reversal controversy not only of the AHP but also other additive MCDM s.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/









