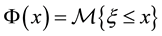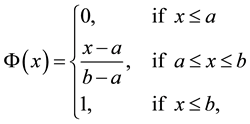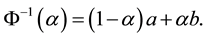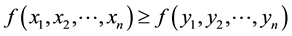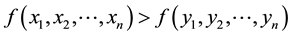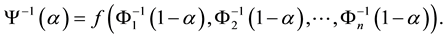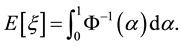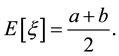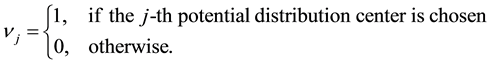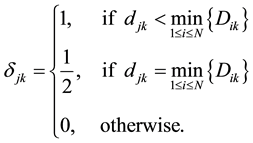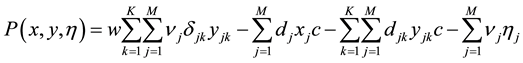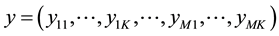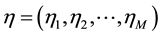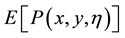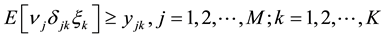American Journal of Operations Research
Vol.05 No.06(2015), Article ID:61509,12 pages
10.4236/ajor.2015.56042
An Uncertain Programming Model for Competitive Logistics Distribution Center Location Problem
Bingyu Lan1, Jin Peng2, Lin Chen3
1College of Mathematics and Sciences, Shanghai Normal University, Shanghai, China
2Institute of Uncertain Systems, Huanggang Normal University, Hubei, China
3Institute of Systems Engineering, Tianjin University, Tianjin, China

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 10 October 2015; accepted 24 November 2015; published 27 November 2015

ABSTRACT
We employ uncertain programming to investigate the competitive logistics distribution center location problem in uncertain environment, in which the demands of customers and the setup costs of new distribution centers are uncertain variables. This research was studied with the assumption that customers patronize the nearest distribution center to satisfy their full demands. Within the framework of uncertainty theory, we construct the expected value model to maximize the expected profit of the new distribution center. In order to seek for the optimal solution, this model can be transformed into its deterministic form by taking advantage of the operational law of uncertain variables. Then we can use mathematical software to obtain the optimal location. In addition, a numerical example is presented to illustrate the effectiveness of the presented model.
Keywords:
Competitive Location, Logistics Distribution Center, Uncertain Programming, Uncertainty Theory

1. Introduction
Research on distribution center location problem is a necessary component of the optimization of logistics distribution’s system. The distribution center plays the role of a bridge that links customers with suppliers so as to transport goods from suppliers to customers. A lot of researches have been devoted to the distribution center location problem. For example, Lu and Bostel [1] investigated a facility location model for logistics system with reverse flows. Klose and Drexl [2] summarized different types of facility location models and their applications to distribution system design.
A large part of location problems have been studied in an ideal environment, in which only a unique facility offers services or products in the market. In practice, with the rapid development of economic, the environment is growing more complex. The facility has to compete with other players for more benefits. Thus the research on competitive location problem plays an important role in location theory. Competitive location problem differs from the general location problem because we must consider the competition between the existing facilities and new facilities. The briefly explain of the competitive location problem is that some facilities have been located in the market and the new facility will be located at the optimal place so as to compete with others for their market share.
Because of the importance of competitive location problem, many scholars devoted to the related research of competitive location problem in deterministic environment, that is, all parameters are known in advance and assumed to be fixed. Hotelling [3] initially introduced the competitive problem of two companies in the market, which laid the foundation for modern competitive location problem. Subsequently, a lot of scholars also studied this topic and made a progress in competitive location theory. In location space aspect, the competitive location problem was extended to the planar location problem by Drezner [4] . Moreover, it was also applied to the network location problem by Hakimi [5] . So Plastria [6] overviewed the papers of competitive location and clarified the location spaces into three traditional spatial settings: discrete space, continuous space and the network. In competition feature aspect, except for the simplest static competitive models, the dynamic models were proposed to describe the action cycles of competing players. Wong and Yang [7] , and Yang and Wong [8] proposed a continuous equilibrium model, respectively. These models solved the competitive location problem with different assumptions of customer demands. With considering the future competition which known in the economic literature as Stackelberg equilibrium problem or leader-follower problem, Plastria and Vanhaverbeke [9] proposed three models to solve Stackelberg equilibrium problem in discrete space. The game theory was introduced into the competitive location problem by Küçükaydin et al. [10] , in which they formulated a bilevel mixed- integer nonlinear programming model to solve the leader-follower problem. Sasaki et al. [11] employed a generic hub arc location model to locate arcs within the framework of Stackelberg. With respect to methodology, various approaches were proposed to obtain the estimate of the market share captured by each competitive facility, such as proximity approach [4] , deterministic utility approach [12] , cover-based approach [13] , and gravity- based approach [14] . For a detailed view of the models of competitive location problem, see Drezner [15] and Plastria [6] .
In practical life, there are many indeterminacy factors in competitive location problem. For example, the demand of customer for a kind of product is variable because it is influenced by other things liked weather. Hence, many scholars established models by stochastic method. Leonardi and Tadei [16] introduced the random utility model into location theory via assuming that the each customer described his utility from a random distribution of utility functions. Subsequently, Drezner and Drezner [17] used the random utility to calculate the expected market share of the competitive facility. In order to overcome the hard of complicated computation of the random utility model, Drezner et al. [18] proved that the random utility model could be approximated by the logit model and designed a procedure to find the best location. Except for the random utility function, some scholars also researched the competitive location problem with stochastic weights in network. Shiode and Drezner [19] analyzed a Stackelberg equilibrium problem on a tree network with stochastic weights and presented a procedure to find the solution. In addition, other papers studied this problem have been published, such as Drezner and Wesolowsky [20] , Shiode and Ishii [21] , and Wesolowsky [22] .
In the above mentioned literatures, these researches cannot be proceeded smoothly without the assumption that there are enough history data to obtain probability distribution which is closed to the real frequency. However, sometimes the lack of history data posed difficulties for applying probability theory, especially when a new product was shipped to the customer by distribution center. In this case, we have to invite some experts to give the belief degree that each event will occur. In order to deal with belief degree, uncertainty theory was found by Liu [23] in 2007, which has become a new tool to describe the human uncertainty.
Within the framework of uncertainty theory, the research of uncertain facility location problem had made a great number of achievements. Gao [24] constructed two uncertain models to deal with single facility location problems on network. Wen et al. [25] proposed an uncertain facility location-allocation model by means of chance-constraints. Wang and Yang [26] investigated two types of uncertain programming models according to different decision criteria for modeling the hierarchical facility location problem in an uncertain environment. Wu and Peng [27] presented an uncertain chance-constrained model to deal with logistics distribution center location problem under uncertain environment.
This paper addresses the problem that a logistics company enters a market by locating a new distribution center where there are many existing competitors in uncertain environment. The demands of customers and setup costs of the potential distribution centers are assumed to be uncertain variables. Then we construct the expected value model with the objective of maximizing the profit of the new distribution center. In order to obtain the optimal solution, the expected value model is transformed into its crisp equivalent model. At last we can use the mathematical software to find the optimal solution.
The innovations of this paper are as follows. We investigate the competitive logistics distribution center location problem under uncertain environment instead of logistics distribution center location problem in uncertain environment. It is different form the problem which dealt with by Wu and Peng [27] . This study is distinguished from the Revelle’s [28] study by making three contributions. Firstly, we assume the customers’ demands are uncertain variables rather than certain amount. Secondly, we study a specific facility rather than any facility, that is, the proposed model can be applied to select logistics distribution center. Thirdly, we describe the customers’ patronizing behavior with a piecewise function instead of a 0 - 1 variable.
The remainder of this paper is organized as follows. We introduce some basic and necessary knowledge about uncertainty theory in Section 2. In Section 3, we state the competitive distribution center location problem and construct an expected value model. In Section 4, we transform the expected value model into its deterministic one. In Section 5, we give a numerical example to illustrate the modeling idea of this paper. At last, the Section 6 concludes the paper.
2. Preliminary
In order to understand the presented model of competitive location problem better, we introduce some necessary knowledge about uncertainty theory in this section.
Let us introduce the concept of uncertain measure first. Let 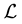 be a σ-algebra over a nonempty set
be a σ-algebra over a nonempty set .
. 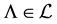 is an event. A set function
is an event. A set function 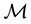 from a σ-algebra
from a σ-algebra 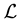 to an interval
to an interval  is an uncertain measure if it satisfies normality axiom, duality axiom, and subadditivity axiom.
is an uncertain measure if it satisfies normality axiom, duality axiom, and subadditivity axiom.
1) (Normality Axiom) 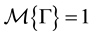 for the universal set
for the universal set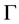 ;
;
2) (Duality Axiom) 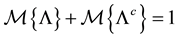 for any
for any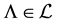 ;
;
3) (Subadditivity Axiom) For every countable sequence of events ,
, 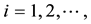 we have
we have
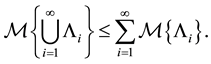
The triplet 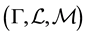 is called an uncertainty space. The product axiom was defined to obtain an uncertain measure of compound event.
is called an uncertainty space. The product axiom was defined to obtain an uncertain measure of compound event.
4) (Product Axiom) Let 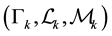 be uncertainty spaces for
be uncertainty spaces for 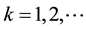

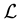
where 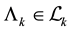
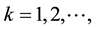
In order to describe the quantities with uncertainty, Liu [23] defined the uncertain variable.
Definition 1. (Liu [23] ) An uncertain variable is a function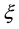
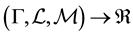
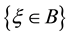
Liu [23] proposed uncertainty distribution to describe uncertain variable analytically.
Definition 2. (Liu [23] ) Let 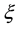
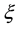
for any number x in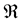
Definition 3. (Liu [29] ) Let 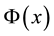
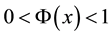
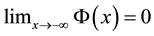
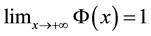
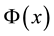
Definition 4. (Liu [29] ) Assume that uncertain variable 
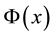
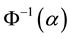
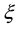
Example 1. If 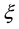
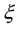
denoted by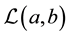

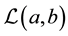
Definition 5. (Liu [30] ) The uncertain variables 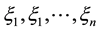
for any Borel sets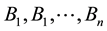
A real-valued function 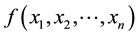
whenever 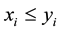
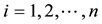
whenever 
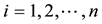
Theorem 1. (Liu [29] ) Let 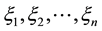

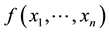
has an inverse uncertainty distribution
We review the important concept of the expected value, which represents the size of uncertain variable.
Definition 6. (Liu [23] ) Let 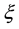
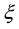
provided that at least one of the two integrals is finite.
Theorem 2. (Liu [29] ) Let 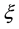
Example 2. Let 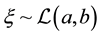
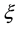
3. The Model of Competitive Location Problem
In this section, we mainly propose the expected value model for competitive distribution center location problem within the framework of uncertain programming. Uncertain programming, proposed by Liu [31] , is a type of mathematical programming which contains uncertain variables.
3.1. Problem Description
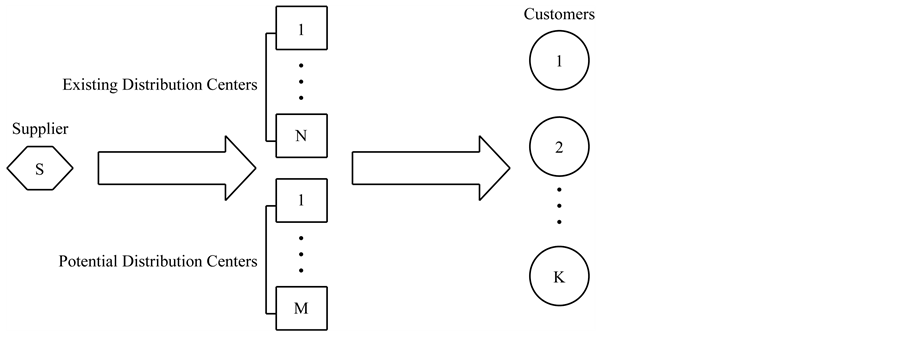
This paper investigates the competitive logistics distribution center location problem in uncertain environment. That is the problem in which a logistics company enters a market by locating a new distribution center where there are many existing distribution centers. The goal of the decision maker is to choose the location of the new distribution center so as to maximize its profit. The flow diagram of logistics distribution is shown in Figure 1. The potential distribution centers in Figure 1 show that they can be selected to build a new distribution center. The setup costs of the potential distribution centers and the demands of customers are assumed to be uncertain variables with known uncertainty distributions. In addition, we assume that the customers patronize the nearest distribution center to meet their full demands.
3.2. Assumptions of Model
Before we begin to study competitive location problem with uncertain variables, we need to make some assumptions as follows (which are referred to Revelle [28] and Wu and Peng [27] ):
1) There is one supplier and many existing distribution centers.
2) The supplier only supplies one kind of product.
3) There is no difference among the products provided by all distribution centers.
4) The location of the new distribution center can be selected from potential distribution centers.
5) The distances between the supplier and potential distribution centers, the distances between potential distribution centers and customers and the distances between existing distribution centers and customers are known in advance.
6) The allocation of customers demands is related to the distance. The full demands of customers will be assigned to the nearest distribution center.
In order to model the competitive location problem, we introduce the following indices and parameters:
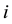
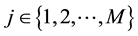
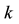

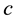
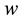
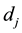
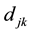
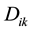
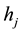
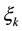
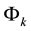
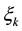
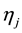

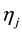
Figure 1. Logistics distribution process.

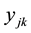
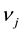
Remark 1: The meaning of variable 
In order to maximize the profit of the new distribution center, the decision maker must choose the appropriate site to build the new distribution center which attracts more customers. The majority of competitive location models assumed that customers will patronize the nearest distribution center. It is rationally for customers who want to sustain the less travel cost. In this paper, we consider that the customers choose the distribution center according to the distance between their sites and distribution centers rather than other conditions, such as price, service and attractiveness.
Thus we assume that the customers patronize the nearest distribution center, and this assumption which has been used by Revelle [28] . This patronizing behavior rule implies that the full demands of each customer are satisfied by the nearest distribution center. The meaning of patronizing behavior which was proposed by Revelle [28] is listed in the following. If the new distribution center is nearer than all existing distribution centers, then the customers choose the new distribution center to satisfy their demands. If they have the same distance, then the half demands of customers are satisfied by the new distribution center. Otherwise, the customers choose the existing distribution center. In Revelle’s [28] model, the customers’ patronizing behavior is embodied in objective function. It used two auxiliary variables to represent the facility which attracts full demands of customers and the facility which attracts half demands of customers, respectively. Our study is distinguished from the Revelle’s [28] study by making the following important contribution: we use a function 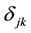
3.3. Expected Value Model
We note that the total profit of the new distribution center is made up of four parts. Thus the total profit is a function related to x, y and
where
and
are decision vectors, and
is an uncertain vector.
Since we know the uncertain objective function 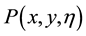
We employ the uncertain programming model to study the competitive logistics distribution center location problem. So we can build the expected value model as follow:

where 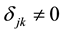
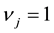

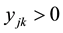
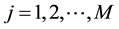
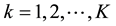
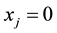

In this expected value model, the first constraint means that the quantity supply is not exceed the demand of customer. The second constraint implies the volume of transport is less than the capacity of the new distribution center. The third one shows that we select single site to build the new distribution center. And the last one ensures the nonnegativity of decision variables 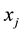
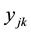
4. The Crisp Equivalent Model
The key problem of the model is seeking for the optimal solution. Taking advantage of the operational law of uncertain variable, we can transform the expected value model (1) into its deterministic form. It is clearly that the total profit function is strictly decreasing with setup costs. According to Theorem 1 and Theorem 2, the objective function
can be converted into

Similarly, the first constraint
can be turned into
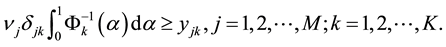
It follows from the formulas (2) and (3) that expected value model (1) can be switched to the following equivalent model:

Clearly, we note that the equivalent model (4) is a deterministic programming model. As all know, the software Lingo cannot show the integral function. Therefore, we can find the optimal solution by using the mathematical software Matlab. In addition, in uncertainty theory, the inverse distribution function is easy to calculate for us. Thus we can calculate the inverse distribution function before we use the software Lingo to find the optimal solution. We can choose one of them to solve this programming. For convenience, the following example is seeking for solution by Lingo.
5. Numerical Example
In order to illustrate the modeling idea and the effectiveness of this model, we give a numerical example in this section. Suppose that there is a supplier in a city. And there are 3 distribution centers to distribute the new model of the televisions to 7 customers. A logistics company want to select an optimal site from 4 potential distribution centers after survey. The distances dj, djk and Dik are listed in Table 1, Table 2 and Table 3, respectively. The unit transportation cost c = 0.01 and the unit product profit w = 5 are given via survey.
Table 1. The distance dj between supplier and potential distribution centers.
Table 2. The distance Dik between existing distribution centers and customers.
Table 3. The distance djk between potential distribution centers and customers.
Table 4. The capacities hj and setup costs ηj of potential distribution centers.
Table 5. The demands ξk of customers.
According to the model (4), the expected value model of this numerical example is listed in the following formula

Then we use Lingo to get the optimal solution which is listed in the following.
Figure 2. Location and distribution plan.
The solution 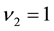
6. The Crisp Equivalent Model
In the process of practical logistics network optimization, uncertain factors often appear in competitive logistics distribution center location problem because of lacking of or even without historical data. This paper investigated a useful model to handle competitive logistics distribution center location problem with uncertain customers demands and uncertain setup costs. The mathematical model of this problem was established by uncertain programming based on the expected value criterion. In order to solve this model, we took advantage of the properties of uncertain variable. Then the expected value model was transformed into its crisp equivalent model, and we used mathematical software Lingo to find its optimal solution. At last, a numerical example was presented to illustrate the effectiveness of the proposed model.
This paper only considers the demands of customers and setup costs of new distribution center are uncertain variables. Indeed, other uncertain factors in competitive logistics distribution center location problem are worthy of studying. We can further focus on the uncertain utility which can be used to describe the uncertainty of customers’ patronizing behavior. Furthermore, we can seek for the expression of uncertain utility. In this paper, we only center on the static competition. It is necessary for further research to consider dynamic competition problem. Thus we can establish dynamic uncertain programming model for uncertain dynamic competitive facility location problem.
Acknowledgements
This work was supported by the Projects of the Humanity and Social Science Foundation of Ministry of Education of China (No. 13YJA630065), and the Key Project of Hubei Provincial Natural Science Foundation (No. 2012FFA065).
Cite this paper
BingyuLan,JinPeng,LinChen, (2015) An Uncertain Programming Model for Competitive Logistics Distribution Center Location Problem. American Journal of Operations Research,05,536-547. doi: 10.4236/ajor.2015.56042
References
- 1. Lu, A. and Bostel, N. (2007) A Facility Location Model for Logistics Systems including Reverse Flows: The Case of Remanufacturing Activities. Computers & Operations Research, 34, 299-323.
http://dx.doi.org/10.1016/j.cor.2005.03.002 - 2. Klose, Z. and Drexl, A. (2005) Facility Location Models for Distribution System Design. European Journal of Operational Research, 162, 4-29.
http://dx.doi.org/10.1016/j.ejor.2003.10.031 - 3. Hotelling, H. (1929) Stability in Competition. Economic Journal, 39, 41-57. http://dx.doi.org/10.2307/2224214
- 4. Drezner, Z. (1982) Competitive Location Strategies for Two Facilities. Regional Science and Urban Economics, 12, 485-493.
http://dx.doi.org/10.1016/0166-0462(82)90003-5 - 5. Hakimi, S. (1983) On Locating New Facilities in a Competitive Environment. European Journal of Operational Research, 12, 29-35.
http://dx.doi.org/10.1016/0377-2217(83)90180-7 - 6. Plastria, F. (2001) Static Competitive Facility Location: An Overview of Optimisation Approaches. European Journal of Operational Research, 129, 461-470.
http://dx.doi.org/10.1016/S0377-2217(00)00169-7 - 7. Wong, S. and Yang, H. (1999) Determining Market Areas Captured by Competitive Facilities: A Continuous Equilibrium Modeling Approach. Journal of Regional Science, 39, 51-72.
http://dx.doi.org/10.1111/1467-9787.00123 - 8. Yang, H. and Wong, S. (2000) A Continuous Equilibrium Model for Estimating Market Areas of Competitive Facilities with Elastic Demand and Market Externality. Transportation Science, 34, 216-227.
http://dx.doi.org/10.1287/trsc.34.2.216.12307 - 9. Plastria, F. and Vanhaverbeke, L. (2008) Discrete Models for Competitive Location with Foresight. Computers & Operations Research, 35, 683-700.
http://dx.doi.org/10.1016/j.cor.2006.05.006 - 10. Küçükaydin, H., Aras, N. and Altnel, I. (2012) A Leader-Follower Game in Competitive Facility Location. Computers & Operations Research, 39, 437-448.
http://dx.doi.org/10.1016/j.cor.2011.05.007 - 11. Sasaki, M., Campbell, J., Krishnamoorthy, M. and Ernst, A. (2015) A Stackelberg Hub Arc Location Model for a Competitive Environment. Computers & Operations Research, 47, 27-41.
http://dx.doi.org/10.1016/j.cor.2014.01.009 - 12. Drezner, T. (1994) Locating a Single New Facility among Existing Unequally Attractive Facilities. Journal of Regional Science, 34, 237-252.
http://dx.doi.org/10.1111/j.1467-9787.1994.tb00865.x - 13. Drezner, T., Drezner, Z. and Kalczynski, P. (2011) A Cover-Based Competitive Location Model. Journal of the Operational Research Society, 62, 100-113.
http://dx.doi.org/10.1057/jors.2009.153 - 14. Huff, D. (1966) A Programmed Solution for Approximating an Optimum Retail Location. Land Economics, 42, 293-303.
http://dx.doi.org/10.2307/3145346 - 15. Drezner, T. (2014) A Review of Competitive Facility Location in the Plane. Logistics Research, 7, 114-126.
http://dx.doi.org/10.1007/s12159-014-0114-z - 16. Leonardi, G. and Tadei, R. (1984) Random Utility Demand Models and Service Location. Regional Science and Urban Economics, 14, 399-431.
http://dx.doi.org/10.1016/0166-0462(84)90009-7 - 17. Drezner, T. and Drezner, Z. (1996) Competitive Facilities: Market Share and Location with Random Utility. Journal of Regional Science, 36, 1-15.
http://dx.doi.org/10.1111/j.1467-9787.1996.tb01098.x - 18. Drezner, T., Drezner, Z. and Wesolowsky, G. (1998) On the Logit Approach to Competitive Facility Location. Journal of Regional Science, 38, 313-327.
http://dx.doi.org/10.1111/1467-9787.00094 - 19. Shiode, S. and Drezner, Z. (2003) A Competitive Facility Location Problem on a Tree Network with Stochastic Weights. European Journal of Operational Research, 149, 47-52.
http://dx.doi.org/10.1016/S0377-2217(02)00459-9 - 20. Drezner, Z. and Wesolowsky, G. (1981) Optimal Location Probabilities in the Distance Weber Problem. Transportation Science, 15, 85-97.
http://dx.doi.org/10.1287/trsc.15.2.85 - 21. Shiode, S. and Ishii, H. (1991) A Single Facility Stochastic Location Problem under a Distance. Annals of Operations Research, 31, 469-478.
http://dx.doi.org/10.1007/BF02204864 - 22. Wesolowsky, G. (1977) Probabilistic Weights in the One Dimensional Facility Location Problem. Management Science, 24, 224-229.
http://dx.doi.org/10.1287/mnsc.24.2.224 - 23. Liu, B. (2007) Uncertainty Theory. Spinger-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-540-73165-8_5 - 24. Gao, Y. (2012) Uncertain Models for Single Facility Location Problems on Networks. Applied Mathematical Modelling, 36, 2592-2599.
http://dx.doi.org/10.1016/j.apm.2011.09.042 - 25. Wen, M., Qin, Z. and Kang, R. (2014) The α-Cost Minimization Model for Capacitated Facility Location-Allocation Problem with Uncertain Demands. Fuzzy Optimization and Decision Making, 13, 345-356.
http://dx.doi.org/10.1007/s10700-014-9179-z - 26. Wang, K. and Yang, Q. (2014) Hierarchical Facility Location for the Reverse Logistics Network Design under Uncertainty. Journal of Uncertain Systems, 8, 255-270.
- 27. Wu, Z. and Peng, J. (2014) A Chance-Constrained Model of Logistics Distribution Center Location under Uncertain Environment. Advances in Information Sciences and Service Sciences, 6, 33-42.
- 28. Revelle, C. (1986) The Maximum Capture or Sphere of Influence Location Problem: Hotelling Revisited on a Network. Journal of Regional Science, 26, 343-358.
http://dx.doi.org/10.1111/j.1467-9787.1986.tb00824.x - 29. Liu, B. (2010) Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty. Spinger-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-13959-8 - 30. Liu, B. (2009) Some Research Problems in Uncertainty Theory. Journal of Uncertain Systems, 3, 3-10.
- 31. Liu, B. (2009) Theory and Practice of Uncertain Programming. Spinger-Verlag, Berlin.