Received 28 March 2015; accepted 8 May 2015; published 12 May 2015

ABSTRACT

This paper provides a gradient search algorithm for finding the maximal visible area polygon (VAP) viewed by an interior point in a simple polygon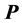. The algorithm is based on a natural partition of 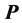into convex sets, such that each element of the partition is associated with a unique analytical form of the area function. We call this partition a back diagonal partition of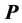. Our maximal VAP algorithm converges in a finite number of steps, and is polynomial with a complexity of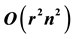, for a simple polygon 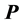with n vertices, and r reflex vertices. We use the maximal VAP algorithm as a basis for a greedy heuristic for the well known guardhouse problem with a computation complexity of.

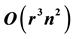Keywords:

Maximal Visible Polygon, Gradient Search, Continuous Optimization, Guardhouse Problem

1. Introduction

A visual polygon is a polygon in which any pair of points is mutually visible. A visible polygon from a point 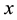in a simple polygon 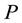with 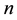vertices can be found with a computational complexity of 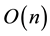by the algorithm of El Gindy and Avis [1] . For each visible polygon, one may associate a real number representing its area. The area function over all points 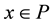is not well behaved, being in general neither convex nor concave, including points that may be not differentiable and even discontinuous. Some properties of polygonal area functions may be found in [2] .

The first problem we intend to solve is finding an interior point 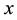that maximizes the area of the visual polygon. We denote this problem as the maximal visible area polygon (VAP) problem. This problem was studied by Cheong et al. [3] , which suggested sampling a finite number of points inside the polygon found by its triangulation.

The algorithm we suggest for this problem is based on a gradient search which converges with a finite number of steps. In order to determine the size of each step taken in the gradient direction, we use a specialized partition of the polygon 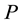into convex sets referred to as a back diagonal partition (BDP). This decomposition arises naturally through the introduction of “back diagonals” in such a manner that the area functional expression is invariant within the domain of each element of the partition. Gradient information along with jump points is combined in an algorithm which traces a path from some initial point in the polygon to a local maximal point. 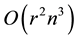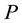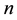The developed algorithm has a computational complexity of for a polygon with vertices and reflex vertices. Such a path may be used to guide a mobile search robot in an enclosed 2D area.

A related problem of placing the minimum number of stationary guards to visually cover a room represented as a 2D polygon was first presented by Klee in 1973 [4] as the art gallery or guardhouse problem. The objective was to find the smallest set of points in a polygon, such that every point inside the polygon would be visible to at least one point in the set. Two points are visible to each other, if the line of sight connecting them lies inside the polygon. Several heuristics and complexity calculations are provided in [5] and [6] for different extensions of the guardhouse problems in which the observers are restricted to the vertices of the polygon, and the edges of the polygon, or not restricted at all. In this paper, we offer a greedy algorithm, which repeatedly uses the gradient search method for finding the maximal VAP, and for solving the guardhouse problem. This greedy heuristic terminates after a finite number of steps and is polynomial with time complexity of. Although the original problem was described in terms of the positioning of guards, it had application to the positioning of surveillance cameras, motion sensors or other detection devices in enclosed environments. We assume that omni vision cameras (or several back to back cameras) are placed at the selected positions. This problem has recently become a popular security problem. For example, currently England has 5 million CCTV security cameras and is adding them at the rate of 100 per day in both inside and outside environments.

In Section 2, we define the maximal VAP problem and introduce useful notation. In Section 3, we introduce the concept of a hidden region, its area, and a back diagonal partition. These set the stage for the introduction of the maximal visible area polygon (VAP) gradient search algorithm described in Section 4. In Section 5, we use the gradient maximal VAP algorithm to form a basis for a greedy algorithm to solve an application in the form of the guardhouse problem, and illustrate it with a small example. Section 6 provides conclusions and future work.

2. Problem Definition and Notation

Before embarking on a formal definition of the problem we present a number of definitions and associated notation. A polygon is a closed plane figure bounded by at least three straight connected line segments. A polygon containing line segments can be described using the vertices along its boundary. Let denote a directed edge between adjacent vertices of where, and. A simple polygon is a polygon which does not contain any holes and whose edges do not intersect. Two points and in are mutually visible if for all points such that, , lie within. A vertex of is said to be non-convex or reflexive if the angle between the two segments that share it as endpoints is greater than when viewed from the interior of. Reflex vertices can create hidden areas when viewed from some points inside the polygon. Figure 1(a) shows a simple polygon where vertex is a reflex vertex, inducing a hidden area with respect to an observation point.

We define as a visibility polygon, such that each point in is visible by an observation point. The area of is denoted as. When understood these will be written simply as and. Given a polygon of size, and a point inside, the visible polygon and its area can be determined with a time complexity of [1] .

The Maximal VAP Problem

Define a maximal visible area polygon (VAP) problem as finding a point for which is maximal, i.e.

The expression for the signed area of a polygon, with vertex coordinates reduced modulo , , is

Note, that represents the signed area of the polygon, i.e., if the vertices of are indexed in counterclockwise order. The visible area function over all is not well behaved, being in general neither convex nor concave. Moreover, it may contain points that are not only non differentiable but discontinuous. For the example in Figure 2(c), the top flat square has a non differentiable boundary and discontinuous drops at its corners.

3. Local Maximal Visible Area Polygon (VAP) Gradient Search Algorithm

We propose a gradient search method which starts with a given observation point, and moves it in the direction of the maximal gradient until a local maximum is achieved. At each step of the algorithm, a different visible area is calculated (i.e. the polygon minus the hidden regions) as a function of the current point. The result of a step in the maximal area gradient direction will give the coordinates of the new observation point. Since there are several local gradients (one for each hidden region), the final direction is determined by the resultant vector. For example, if polygon has two hidden regions with respect to a given point, then two gradients are calculated (one for each hidden area). If the gradients for hidden regions I and II are and, respectively, then the final gradient will be. Below we present several definitions, which will form the basis of a gradient search method to be described subsequently.

3.1. Basic Definitions and Notation

Given a simple polygon with vertices ordered in counterclockwise order, for any three consecutive vertices, , define a turn: as: . We say that is a left turn if is positive, a right turn if is negative, and not a turn otherwise.

Proposition 1 Let a chain be a sequence of connected, nonintersecting line segments. Given two points and, such that the line segment does not intersect any line segment of, then and are said to be mutually visible with respect to chain.

Proposition 2 Let be a simple chain such that and are visible with respect to. If a point is exterior to the region enclosed by and collinear with and, then the region

enclosed by is not visible from. The proof appears in [1] .

Figure 1(b) shows an example of a point exterior to a chain. The point is collinear with and, and therefore, cannot see the region enclosed by. A line segment is

said to be a window of with respect to the region enclosed by. This region is said to be a hidden region with respect to. Note, that if is visible from then so is. We denote the window, of, as a left hand window (LHW) if is a left turn, and as a right hand window (RHW) if is a right turn. Looking back at Figure 1, we can see that is a left turn. Let be a viewpoint inside and a reflex vertex on the boundary of. We classify reflex vertices as active or inactive according to the possibility of each creating an area occluded from. In order to determine whether a reflex vertex is active or inactive with respect to a given viewpoint, we extend the adjacent edges of into the interior of until they hit the boundary to obtain back diagonals and. If and are mutually visible and lies outside the angle, then is said to be an active reflex point, otherwise is inactive. Given a viewpoint and an active reflex point, define a ray from in the direction of and passing through. Let be the set of intersection points of the ray with the boundary of, ordered according to the distance from. Denote the intersection point closest to as a reflection point. Figure 3(a) shows the reflection point (the first intersection point) with respect to a viewpoint and an active reflex vertex.

3.2 Back Diagonal Partition (BDP)

Consider a pair of vertices and on the boundary of, such that is a reflex vertex and is visible from. Define a diagonal as a line segment directed from vertex to vertex. A back diagonal with respect to is a line segment joining the vertex and the point, where is the nearest point on the edge of visible in the reverse direction of. The point is said to be a reflection point on the boundary of visible from along a ray directed from through. Figure 4 shows a back diagonal created by a reflex vertex and a vertex visible from.

Figure 5 shows an example of all back diagonals (dotted lines) induced by the reflex vertices. The introduction of all back diagonals induces a back diagonal partition (BDP) of. Such a partition is a planar graph defining a set of internal regions. Note that five back diagonals are induced by vertex -one for each of the vertices in visible from.

Proposition 3 A BDP of partitions into a collection of regions, each a convex sub polygon of.

Proposition 4 A back diagonal is an edge in a BDP such that viewpoints in the neighborhood on either side of it have different visible and area polygonal functional expressions. Thus, each region in a BDP has a unique visible and area polygonal functional expression.

The above propositions will be useful in construction an algorithm for the maximal VAP problem.

3.3. Hidden Regions

Note that the gray areas in Figure 3 are hidden regions with respect to the viewpoints. We define back edges for two cases. Case 1: If is an interior point of an edge of, then is said to be a reflection point of on through the active reflex vertex, and is called a back edge of through. The edge in Figure 3 is the back edge of the viewpoint through the reflex vertex. Case 2: If coincides with a vertex of, then the back edge is taken as. In this case, and induce a back diagonal on which lies. For ease of exposition, all of the following will be in terms of case 1. Note, that case 1 corresponds to a point that does not lie on a back diagonal with respect to. A left hand hidden region with respect to, a left hand active reflex vertex, a reflection point and its back edge, is a region bounded by the polygon defined by the circular vertex list:

where, and are the original vertices of in CCW order. A right hand hidden region is similarly defined for a right hand reflex vertex as. Figure 3(b) provides an illustration of and for a given observation point.

We can now define a visible polygon in terms of the definitions given above. Given a polygon and an observation point, define the visible polygon as the polygon comprised of subsequences of the original vertices of and all windows with respect to. The visible polygon contains all visible vertices and the reflection points of all active reflex vertices with respect to. From proposition 2 it should be clear that the regions enclosed by and are not visible from.

3.4. Calculation Formulas Using Hidden Areas

Define a rectangular coordinate system in such that each point in is represented by a set of ordered real valued coordinates. Given the coordinates of an observation point, the end points of back edge, and an active reflex point, the reflection point can be calculated as a function of and has the general form:

Here, are constants in terms of the points and. The hidden area as a function of (the reflection point) has the following form:

Here, are constants comprised of the coordinates of the original boundary vertices of. This is a direct result of applying Equation (2) to the boundary vertices,

of the left and right hidden regions, respectively. Given a point in, associate with it a set of active reflex vertices. Let and represent the number of left and right reflex vertices with respect to. Each active reflex vertex has an associated hidden region. Let represent a left/ right hidden regions of associated with an active reflex vertex, respectively.

The collection of left and right hand hidden regions associated with are denoted as; and, respectively. Since intersections of hidden regions are empty (except for possible vertex points), the area of the visible polygon may be represented as follows:

This area function will be derived in terms of the rectangular coordinates of point, in order to determine the directional move of, such as to increase the visible area. For example, Figure 6 shows a polygon, with a, and a visible polygon .

Let represent the area of the visible polygon associated with the view point and a left hand hidden region. Using and isolating the coordinates we get the area in terms of:

The only relevant vertices are the reflex vertex (which created the hidden region) and which is the visible vertex of the edge, the back edge of through. Note that is the intersection point between the line collinear with and. Repeating the process for a right hand side region, where is the visible vertex of the back edge we obtain:

The individual coordinates of can be convex or concave, increasing or decreasing or constant in and depending on the orientation of the ray and the back edge.

4. Gradient Search Algorithm for Maximal VAP

Following are the steps of a gradient search algorithm for finding a local max to the maximal visible polygon problem. Given the current point, the algorithm finds the maximal gradient direction and moves until one of a number of events occurs. These events are determined when the functional form of the area function undergoes a change if the move is continued. This occurs, for example, when the point hits a back diagonal or an original edge of. Also, when the refection point moves to an end point of its back edge, or when a new reflex point becomes active. At any of these events a new area function is introduced and the gradient is recalculated to determine a new movement direction.

4.1. Determination of the Maximal Gradient Direction

Since and depend on the view point, we must rephrase the area’s formulation using its coordinates. To do this two lines are constructed: (connecting and) and (collinear with the back edge) (see Figure 5). The intersection of and is the point. The right side of (9) contains functions of.

The total gradient is the sum of the partials for all active reflex vertices with respect to.

where, and are all active left and right reflex vertices with respect to, respectively.

4.2. Max VAP Algorithm (the Gradient Search Algorithm)

Although this algorithm is based on movements between sub regions of a BDP, there is no need to actually construct it. It is only necessary to construct the back diagonals (line equations). This is because the algorithm searches for a critical event when the observer crosses a back diagonal. At his point, based on proposition 4, a recalculation of the area and new gradient are necessary.

The Steps of the Procedure

Given a simple polygon, and a point in. Set.

Step 1 Compute the area of as.

Step 2 Determine the visible polygon from and its area. Identify all “active” reflex vertices and the corresponding set of windows:, where is the active reflex vertex, and its reflection point which lies on the interior or endpoint its associated back edge. If, go to Step 7 (Stop).

Step 3 Find the total gradient that maximizes the increase in, using (12) and Proposition 5. If no such gradient exists, stop and go to Step 6.

Step 4 If lies on an original edge of, calculate a new gradient direction so as to slide along the edge in a direction such that the angle between the original gradient direction and the edge is minimal.

Step 5 Move in the gradient direction until one of the following critical events occurs:

a) hits a vertex or edge of.

b) One of the reflection points slides to the endpoint of its back edge (i.e. one of the vertices of).

c) If one of the windows becomes collinear with one of the edges that forms a reflex vertex, i.e.; or for a or window, respectively. This reflex vertex becomes inactive; drop its associated window from.

d) A new reflex vertex becomes active. Add the associated window to.

Step 6 If, compute the new point, and return to Step 2; otherwise, , and the entire polygon is viewable from.

Step 7 Stop. No local improvement is possible. Let be the best point. Compute, the total visible area from.

Note that the events in Step 5 correspond to the intersection of the gradient direction vector and all back diagonals.

Proposition 5 The sequence is increasing in.

Proposition 6 The Gradient Search Algorithm converges in a finite number of steps. This is true since the sequence in Proposition 1 is bounded from above by the area of.

Proposition 7 The gradient search algorithm has a time complexity.

Proof. In Step 2, the initial polygon can be calculated in time. This also identifies all active reflex vertices (bounded by). Finding will requires at most calculations. In Step 3, the movement in the direction of is performed until hitting a boundary edge or back diagonal. This requires calculations to find all intersections between the gradient directional line and all back diagonal lines. Steps 2 and 3 are repeated at most times in moving from back diagonal to back diagonal (resulting in at most points between and as back diagonals are not revisited. Thus, the total time complexity of the gradient search algo-

rithm is.

4.3. Illustrative Example for the Maximal VAP Problem

The example in Figure 7 provides a demonstration of the algorithm for the case of a simple polygon with three reflex vertices, one of them, remaining inactive throughout. The sequence of points and visible areas are, and.

5. Application-Solving the Guardhouse Problem

The guardhouse problem, proven to be NP-Hard in [4] , is defined as the problem of the finding the minimal number of observation points in a given a simple polygon such that, the union of the visible area of all points in equals.

A greedy algorithm is described for solving the guardhouse problem which repeatedly uses the maximal VAP algorithm. The idea is to start with a simple polygon, and remove a maximal VAP. This operation can result in disconnected components, each in itself a simple polygon. The process is repeated for any remaining components. Each removal results in an additional observation point, so that the number of removals equals the number of points needed to view the entire original polygon.

5.1. The Greedy Heuristic

Given a simple polygon, let be a collection of polygons.

1) Initially set, remove from and set it to the current polygon.

2) Start with a random point in. Call the Max VAP gradient search algorithm to find the point, and.

3) Let be the set of simple polygons obtained by subtracting the visibility polygon from. (i.e. the parts of the polygon which are not visible from). Add to the collection of polygons.

4) If stop, otherwise;

5) Select a polygon in and remove it, and return to Step 2.

The greedy heuristic described above terminates after a finite number of steps. The complexity of the greedy heuristic for solving the guardhouse problem is. There are at most visits to Step 2 each requiring a call to the max VAP algorithm. Thus, the time complexity of the greedy heuristic is.

5.2 Illustrative Example

Figure 8(a) shows a sample polygon containing 16 vertices. We start with point shown in (b) and improve it until reaching a local maximum. The visible area is then removed from the initial polygon, and two new sub polygons appear in (c). In (d) and (e), this process is repeated with the two parts left, resulting in the final solution (f) in which the entire polygon is covered by 4 observation points.

6. Conclusions and Future Work

This work defined the maximal VAP problem, and offered a gradient algorithm for its solution which had a time

complexity of. In most practical environments, is much smaller than, such that the complexity can be in fact much closer to. The algorithm was used as a basis for a greedy heuristic procedure for

solving the guardhouse problem with a time complexity of. This heuristic procedure can be used for various applications in the field of homeland security such as placing indoor surveillance cameras or motion sensors. Several small examples are presented to illustrate the procedure.

It will be interesting to compare the results of our suggested procedure to other well-known heuristics for the guardhouse problem offered by other researchers. Such a comparison must include not only the quality of the solution, but also the running times. This is left for future work.

References