American Journal of Operations Research
Vol.4 No.3(2014), Article ID:45683,13 pages DOI:10.4236/ajor.2014.43014
Approaches to Solve MID_CPLP Problem: Theoretical Framework and Empirical Investigation
Renduchintala Raghavendra Kumar Sharma1, Pritee Agarwal2
1Department of Industrial and Management Engineering, Indian Institute of Technology, Kanpur, India
2Department of Mathematics and Statistics, Indian Institute of Technology, Kanpur, India
Email: rrks@iitk.ac.in, pritee.iitk@gmail.com, pritee@iitk.ac.in
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 14 March 2014; revised 14 April 2014; accepted 21 April 2014
ABSTRACT
In two-stage warehouse location problem, goods are moved from plants to warehouses at stage-1 (which are larger sized warehouses), and from there to warehouses at stage-2 (which are smaller sized warehouses); and finally to the markets. We aim to minimize the sum of location costs of the warehouses at stage-1 and stage-2; plus the total distribution cost of goods to the markets. In this paper two-stage capacitated warehouse location problem (TSCWLP) is vertically decomposed into the smaller problems, which is attained by relaxing the associated flow balance constraints. This leads to three different versions of Capacitated Plant Location Problem (CPLP) referred as RHS_CPLP, MID_CPLP and LHS_CPLP (Verma and Sharma [1]). In this paper MID_CPLP is reduced to RHS_CPLP and a single constraint 0-1 Knapsack problem by relaxing a difficult constraint. Interesting results and conjectures are given. Later two more valid constraints are added to MID_CPLP which are relaxed further to get additional results.
Keywords:TSCWLP, Location, Transportation, Distribution

1. Introduction and Literature Survey
In country like large geographical area, such as India, distribution of goods such as fertilizer, cement, edible oil, sugar, food grains etc, is close in stages. From large sized plants, goods are moved to larger sized warehouses, from larger sized warehouses to smaller sized warehouses and finally to markets/customers. It is to be decided that where to locate warehouses (among potential locations for large sized warehouses as well as smaller sized warehouses). It is required to minimize sum total of cost of location of warehouse and cost of distribution of goods. Stage wise location-distribution has been attempted by Geoffrion and Graves [2] , Sharma [3] , Sharma and Berry [4] and Verma and Sharma [5] . In this paper we attempt a two-stage warehouse location problem and alongside give a novel method to solve MID_CPLP that results due to vertical decomposition developed for solution. Facility location problems form an important class of integer programming problems, with application in the distribution and transportation industries. In any organization, one of the most important strategic decisions is locating facilities viz. factories, plants or warehouses and their suitable stages. While locating a facility, the most prioritized criterion is a good service level. However, achievement of an economic optimality is also a key decisive factor. Based on the number of stages between the producing facility and the market, there are different types of facility location problems like plant location problem, single-stage/two-stage warehouse location problem. A review of the literature on location problems can be found in (Sahin and Sural [6] , ReVelle and Eiselt [7] , ReVelle, Eiselt and Daskin [8] and Brandeau and Chiu [9] ). Multistage warehouse location problems are frequently occurring in real life; see (Geoffrion and Graves [2] , Sharma [3] and Sharma [10] ). TSCWLP problem has been studied by Verma and Sharma [1] . In Section 2, we give formulation of TSCWLP, few relaxations of MID_CPLP; and also give a few results. In the Section 3 we give empirical investigation and related statistical significance. Finally in Section 4 we conclude.
2. Formulation and Relaxations of TSCWLP
2.1. Problem Formulation of TSCWLP
In this section, we propose the formulation of TSCWLP using the style of Sharma [3] , Sharma and Namdeo [11] , Sharma and Sharma [12] . Verma and Sharma [5] developed a variety of constraints that link real and 0-1 integer variables. They have also developed some strong constraints based on Sharma and Berry [4] .
2.1.1. Index Used
h : set of supply points (plants); 
i : set of potential warehouse points at stage 1; 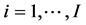
j : set of potential warehouse points at stage 2; 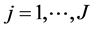
k : set of markets; 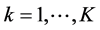
2.1.2. Definition of Constants
Dk : Demand for the commodity at market “k”
dk :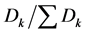 , Demand at market “k” as a fraction of total market demand Sh : Supply available at plant “h”
, Demand at market “k” as a fraction of total market demand Sh : Supply available at plant “h”
sj : , Supply available at plant ‘h’ as a fraction of the total market demand fws1i : Fixed cost of locating a warehouse at “i”
, Supply available at plant ‘h’ as a fraction of the total market demand fws1i : Fixed cost of locating a warehouse at “i”
fws2j : Fixed cost of locating a warehouse at “j”
CAPWS1i : Capacity of a stage 1 warehouse “i”
CAPWS2j : Capacity of a stage 2 warehouse “j”
capws1i : , Capacity of whs-1 at “i”as a fraction of the total market demand capws2j :
, Capacity of whs-1 at “i”as a fraction of the total market demand capws2j : 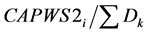 Capacity of whs-2 at “j” as a fraction of the total market demand cpws1hi : Cost of transporting
Capacity of whs-2 at “j” as a fraction of the total market demand cpws1hi : Cost of transporting 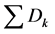 goods from plant “h” to whs-1 “i”
goods from plant “h” to whs-1 “i”
cws1ws2ij : Cost of transporting 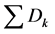 goods from whs-1 “i” to whs2 “j”
goods from whs-1 “i” to whs2 “j”
cws2mjk : Cost of transporting  goods from whs-2 “j” to market “k”
goods from whs-2 “j” to market “k”
2.1.3. Definition of Variables
XPWS1hi : Quantity of commodity transported from plant “h” to whs-1 “i”
xpws1hi :  , Quantity transported from “h” to “i” as fraction of total demand XWS1WS2ij : Quantity of commodity transported from whs-1 “i” to whs-2 “j”
, Quantity transported from “h” to “i” as fraction of total demand XWS1WS2ij : Quantity of commodity transported from whs-1 “i” to whs-2 “j”
Xws1ws2ij : 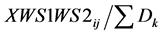 , Quantity transported from “i” to “j” as fraction of total demand XWS2Mjk : Quantity of commodity transported from whs-2 “j” to market “k”
, Quantity transported from “i” to “j” as fraction of total demand XWS2Mjk : Quantity of commodity transported from whs-2 “j” to market “k”
Xws2mjk : 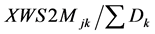 , Quantity transported from “j” to “k” as fraction of total demand yws1i : 1 if stage 1 warehouse is located at “i”, 0 otherwise yws2j : 1 if stage 2 warehouse is located at “j”, 0 otherwise
, Quantity transported from “j” to “k” as fraction of total demand yws1i : 1 if stage 1 warehouse is located at “i”, 0 otherwise yws2j : 1 if stage 2 warehouse is located at “j”, 0 otherwise
2.1.4. Mathematical Formulation
The cost minimization problem for the TSCWLP can be written as mixed 0-1 integer linear programming problem as given in the formulation below.
Objective Function:
Minimize
 (1)
(1)
This can be written as:
Minimize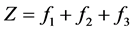 , where
, where
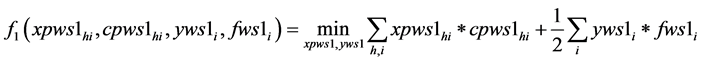
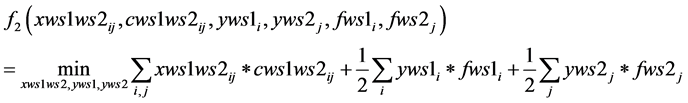

Subject to:
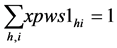 (2)
(2)
 (2a)
(2a)
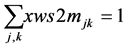 (2b)
(2b)
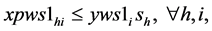 (3a)
(3a)
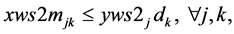 (3b)
(3b)
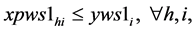 (4a)
(4a)
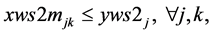 (4b)
(4b)
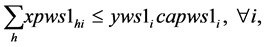 (5)
(5)
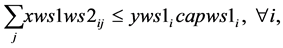 (5a-i)
(5a-i)
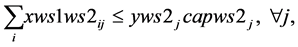 (5a-ii)
(5a-ii)
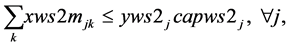 (5b)
(5b)
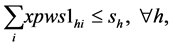 (6)
(6)
 (6a-i)
(6a-i)
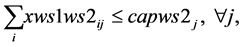 (6a-ii)
(6a-ii)
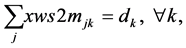 (6b)
(6b)
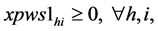 (7)
(7)
 (7a)
(7a)
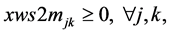 (7b)
(7b)
 (8a)
(8a)
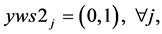 (8b)
(8b)
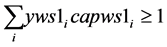 (9a)
(9a)
 (9b)
(9b)
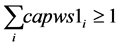 (10a)
(10a)
 (10b)
(10b)
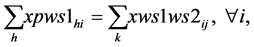 (11a)
(11a)
 (11b)
(11b)
Since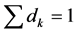 , constraints 2, 2(a) and 2(b) ensure that flow across stages is equal to total demand by all the markets. Constraints 3(a) and 3(b) are strong linking constraints (see Sharma and Berry [4] and Verma and Sharma [5] ). Equations 4(a) and 4(b) are weak linking constraints. Equations 5, 5(a-i), 5(a-ii) and 5(b) strong capacity constraints (see Sharma and Berry [4] ). Equation 6 ensures the flow from plant is less than supply available at that plant. Equations 6(a-i) and 6(a-ii) ensure that throughput form a warehouse is less than or equal to its capacity. Equation 6(b) ensures that the quantity received at a market is equal to its demand. Equations 7, 7(a) and 7(b) are non-negativity restrictions on real variables. Equations 8(a) and 8(b) are 0-1 restrictions on binary location variables. Equations 9(a) and 9(b) ensure that located capacity is more than or equal to the total demand of the markets. Equations 10(a) and 10(b) ensure that total average capacity is more than market demand at each stage. Equations 11(a) and 11(b) are flow balance constraints (inflow is equal to outflow) at each of the warehouses. By relaxing different constraints, various relaxations can be obtained as Lagrangian relaxation (LR). LR is a relaxation technique, which works by moving hard constraints into the objective to impose a penalty on the objective if they are not satisfied. This is easier to solve than the original problem. An optimal objective value of the Lagrangian relaxed problem, for a given set of multipliers, provides a lower bound (in the case of minimization) for the optimal solution to the original problem. The best lower bound can be derived by updating the multipliers by a dual ascent procedure. An upper bound on the optimal solution of the original problem can be derived by using the information obtained from the LR to construct a feasible solution to the original problem. This is normally done by applying some heuristic. In the next section, we present vertical decomposition approach for solving TSCWLP and variety of LR and LP relaxations.
, constraints 2, 2(a) and 2(b) ensure that flow across stages is equal to total demand by all the markets. Constraints 3(a) and 3(b) are strong linking constraints (see Sharma and Berry [4] and Verma and Sharma [5] ). Equations 4(a) and 4(b) are weak linking constraints. Equations 5, 5(a-i), 5(a-ii) and 5(b) strong capacity constraints (see Sharma and Berry [4] ). Equation 6 ensures the flow from plant is less than supply available at that plant. Equations 6(a-i) and 6(a-ii) ensure that throughput form a warehouse is less than or equal to its capacity. Equation 6(b) ensures that the quantity received at a market is equal to its demand. Equations 7, 7(a) and 7(b) are non-negativity restrictions on real variables. Equations 8(a) and 8(b) are 0-1 restrictions on binary location variables. Equations 9(a) and 9(b) ensure that located capacity is more than or equal to the total demand of the markets. Equations 10(a) and 10(b) ensure that total average capacity is more than market demand at each stage. Equations 11(a) and 11(b) are flow balance constraints (inflow is equal to outflow) at each of the warehouses. By relaxing different constraints, various relaxations can be obtained as Lagrangian relaxation (LR). LR is a relaxation technique, which works by moving hard constraints into the objective to impose a penalty on the objective if they are not satisfied. This is easier to solve than the original problem. An optimal objective value of the Lagrangian relaxed problem, for a given set of multipliers, provides a lower bound (in the case of minimization) for the optimal solution to the original problem. The best lower bound can be derived by updating the multipliers by a dual ascent procedure. An upper bound on the optimal solution of the original problem can be derived by using the information obtained from the LR to construct a feasible solution to the original problem. This is normally done by applying some heuristic. In the next section, we present vertical decomposition approach for solving TSCWLP and variety of LR and LP relaxations.
2.2. Lagrangian Relaxation of TSCWLP
Proceeding in a manner similar to Verma and Sharma [13] , TSCWLP is also vertically decomposed into three sub problems viz. LHS_CPLP, MID_CPLP and RHS_CPLP. In this approach, stages of warehouses are vertically decomposed to get smaller sized problems, which are relatively easier to solve. 1st LR of this formulation is obtained by relaxing flow balance constraints (11(a)) and (11(b)) with suitable multipliers ![]() and
and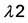 respectively. In main problem, we note that constraint set (11(a)) connects the “xpws1hi” and “xws1ws2ij” variables. Similarly, constraint set (11(b)) connects the “xws1ws2ij” and “xws2mjk” variables. If these two sets of constraints are relaxed, main problem will be separated into three sub-problems. One problem with “xpws1hi” and “yws1i”, called as LHS_CPLP, the other with “xws1ws2ij”, “yws1i” and “yws2j” to be called as MID_CPLP, and the last problem with “xws2mjk” and “yws2j” called as RHS_CPLP. Verma and Sharma [13] have already attempted RHS_CPLP and LHS_CPLP. Here different relaxations of MID_CPLP are developed and relationship is obtained for them.
respectively. In main problem, we note that constraint set (11(a)) connects the “xpws1hi” and “xws1ws2ij” variables. Similarly, constraint set (11(b)) connects the “xws1ws2ij” and “xws2mjk” variables. If these two sets of constraints are relaxed, main problem will be separated into three sub-problems. One problem with “xpws1hi” and “yws1i”, called as LHS_CPLP, the other with “xws1ws2ij”, “yws1i” and “yws2j” to be called as MID_CPLP, and the last problem with “xws2mjk” and “yws2j” called as RHS_CPLP. Verma and Sharma [13] have already attempted RHS_CPLP and LHS_CPLP. Here different relaxations of MID_CPLP are developed and relationship is obtained for them.
2.2.1. LHS_CPLP
 (1(a))
(1(a))
s.t.: (2), (3), (4), (5), (6), (7), (8(a)), (9(a)), (10(a)).
2.2.2. MID_CPLP
 (1(b))
(1(b))
s.t.: (2(a)), (5(a-i)), (5(a-ii)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (8(b)), (9(b)), (10(b)).
2.2.3. RHS_CPLP
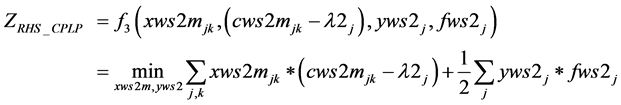 (1(c))
(1(c))
s.t.: (2(b)), (3(b)), (4(b)), (5(b)), (6(b)), (7(b)), (8(b)), (9(b)) and (10(b)).
2.2.4. Original relaxed TSCWLP
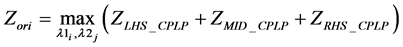 (1(d))
(1(d))
s.t.: (2)-(7), (2(a)), (5(a-i)),(5(a-ii)), (6(a-i)), (6(a-ii)), (7(a))-(10(a)), (2(b))-(10(b)).
We focus on MID_CPLP in this chapter.
2.3. A Few Theoretical Results on MID_CPLP
We relax constraint (5(a-ii)) by attaching multiplier 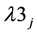 to get,
to get,
2.3.1. MID_CPLP (λ3j)
 (1(e))
(1(e))
s.t.: (2(a)), (5(a-i)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (8(b)), (9(b)), (10(b)).
 problem will be separated into two sub-problems:
problem will be separated into two sub-problems:  (Verma and Sharma [5] ) and one 0-1 knapsack problem (single constraint).
(Verma and Sharma [5] ) and one 0-1 knapsack problem (single constraint).
1) CPLP_R (λ3j)
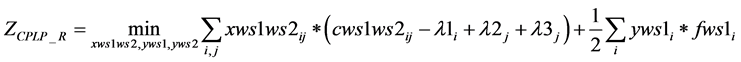 (1(f))
(1(f))
s.t.: (2(a)), (5(a-i)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (10(b)).
2) 0-1_KSP (λ3j)
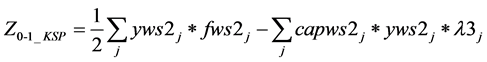 (1(g))
(1(g))
s.t.: (8(b)), (9(b)).
2.3.2. Relaxation of CPLP_R (λ3j)
Now  is attempted in literature by three different relaxations. They are R1, R2 and R3 respectively. When integrality restriction on yws1i is relaxed we obtain (12(a)).
is attempted in literature by three different relaxations. They are R1, R2 and R3 respectively. When integrality restriction on yws1i is relaxed we obtain (12(a)).
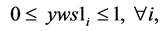 (12(a))
(12(a))
1) CPLP_R1 (λ3j)
(1(f)); Subject to: (2(a)), (5(a-i)), (6(a-i)), (6(a-ii)), (7(a)), (10(a)), (10(b)) and (12(a)).
Result 1: R1 is equal to strong LP relaxation of 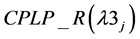 (Sharma and Berry [4] , Verma and Sharma [5] ). Here the restriction on yws1i is relaxed by (12(a)).
(Sharma and Berry [4] , Verma and Sharma [5] ). Here the restriction on yws1i is relaxed by (12(a)).
Proof: It is easy to see.
2) CPLP_R2 (λ3j)
In this LR a constraint introducing upper (PU1) and lower (PL1) limits on the number of open plants is added up, Cornuejols, Sridharan and Thizy [14] i.e.
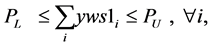 (13(a))
(13(a))
This LR was proposed first by Christofides and Beasley [15] and later used Verma and Sharma [5] among others and is obtained by dualizing (2(a)) and (6(a-ii)). Let λxws1ws2, λxws1ws2j be the Lagrangian multipliers associated with (2(a)) and (6(a-ii)) respectively.
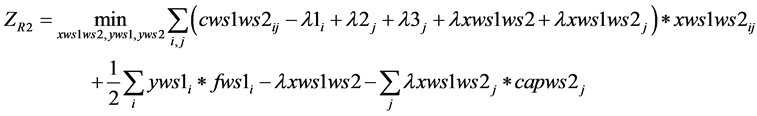 (1(h))
(1(h))
Subject to: (5(a-i)), (6(a-i)), (7(a)), (10(a)), (10(b)), (8(a)) and (13(a)).
3) CPLP_R3 (λ3j)
(1(h)); Subject to: (5(a-i)), (6(a-i)), (7(a)), (8(a)), (9(a)), (10(a)) and (10(b)). It is also attempted by first by Nauss [16] and later by Verma and Sharma [5] . We have following result due to Verma and Sharma [5] .
Result 2: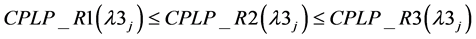 .
.
If we add the objective function value of the 0-1 knapsack problem in the objective value of CPLP_R then we get the objective value of the MID_CPLP_R. Hence, the same relaxation along with their relative strength is used for MID_CPLP here in form of theorem 2 below.
Result 3: 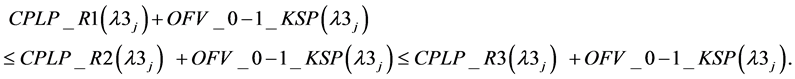
where OFV stands for objective function value of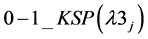 . Hence we have Theorem 1: For any value of
. Hence we have Theorem 1: For any value of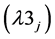 ,
, 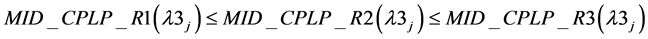 .
.
This theorem provides the relative effectiveness of the bounds that may be obtained for these relaxations of MID_CPLP. Verma and Sharma [5] have shown that difference between R2-R1 and R3-R2 is significant. Hence we have the result given below.
Result 4: Difference between 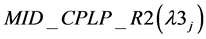 and
and 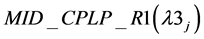 &
&  and
and 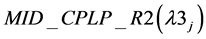 is significant.
is significant.
Now we add two new constraints to the MID_CPLP. They are as follows.
 (14)
(14)
 (15)
(15)
We get the modified and a valid formulation of MID_CPLP i.e., MO_MID_CPLP as given below.
2.3.3. MO_MID_CPLP
 (1(i))
(1(i))
s.t.: (2(a)), (5(a-i)), (5(a-ii)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (8(b)), (9(b)), (10(b)), (14) and (15).
Now we relax the constraints (5(a-ii)), (14) and (15) by attaching multiplier λ3j, λ4ij and λ5ij respectively to get the following.
1) MO_MID_CPLP_R (λ3j, λ4ij, λ5ij)
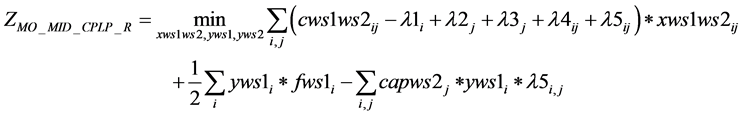 (1(j))
(1(j))
s.t.: (2(a)), (5(a-i)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (10(b)).
2) MO_0-1_KSP (λ3j, λ4ij, λ5ij)
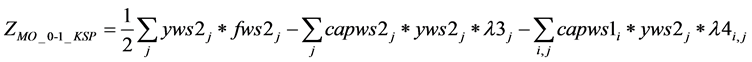 (1(k))
(1(k))
s.t.: (8(b)), (9(b)).
3) Relaxation of MO_MID_CPLP_R (λ3j, λ4ij, λ5ij)
Now MO_MID_CPLP_R 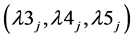 can be attempted by three different relaxations. They are R1, R2 and R3 respectively as before.
can be attempted by three different relaxations. They are R1, R2 and R3 respectively as before.
Result 5: We get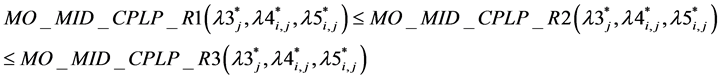 .
.
Theorem 2: For optimal value of ,
, 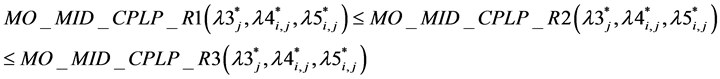 .
.
Result 6: Differences between MO_MID_CPLP_R2 and MO_MID_CPLP_R1 & MO_MID_CPLP_R3 and MO_MID_CPLP_R2 are statistically significant.
Now since R1 is LP relaxation, it easily follows that
Theorem 3: 
In R2: we solve single constraint bounded variable LP to get a factor that is added to 0-1 single constraint knapsack problem (which is solved by inspection) (see Christifides and Beasley [15] ). A priori it is observed that the process is complicated enough and is NOT amenable to theoretical result (for determining the difference between MID_CPLP (R2) and MO_MID_CPLP (R2).
In R3: we solve several continuous knapsack problems & their objective function value is fed to a 0-1 knapsack problem (see Nauss [16] ). This is also complicated enough; and theoretical result may NOT be possible (for determining the difference between MID_CPLP (R3) and MO_MID_CPLP (R3)).
Hence, we may have to determine differences empirically (by coding R2 and R3 for different Lagrangian Relaxations). However, as warehouse capacities are more constrained, MO_MID_CPLP for both R2 and R3 will give significantly superior lagrangian lower bounds at little computational expense. However, we do have a theoretical result for R1 (for difference between MID_CPLP and MO_MID_CPLP) which a LP relaxation. Hence we have the following Conjectures.
Conjecture 1: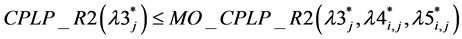 .
.
Conjecture 2: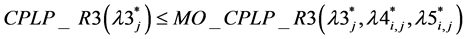 .
.
If only (14) is added to MID_CPLP then we get MO1_MID_CPLP. Several similar results are given without much discussion as they are obvious.
2.3.4. MO1_MID_CPLP
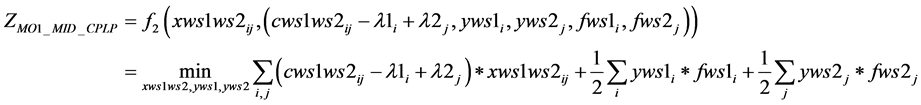 (1(m))
(1(m))
s.t.: (2(a)), (5(a-i)), (5(a-ii)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (8(b)), (9(b)), (10(b)), (14).
Now we relax the constraints (5(a-ii)) and (14) by attaching multiplier  and
and 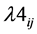 respectively to get the following.
respectively to get the following.
1) 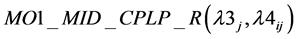
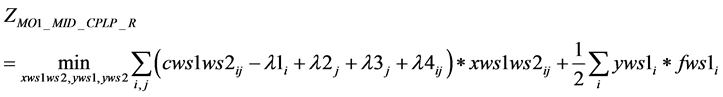 (1(n))
(1(n))
s.t.: (2(a)), (5(a-i)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (10(b)).
2) 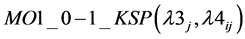
 (1(o))
(1(o))
s.t.: (8(b)), (9(b)).
3) Relaxation of 
Now 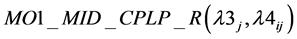 can be attempted by three different relaxations. They are R1, R2 and R3 respectively as before.
can be attempted by three different relaxations. They are R1, R2 and R3 respectively as before.
Result 7: We get .
.
Theorem 4: For optimal value of ,
, 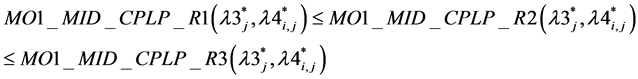 .
.
Result 8: Differences between MO1_MID_CPLP_R2 and MO1_MID_CPLP_R1 & MO1_MID_CPLP_R3 and MO1_MID_CPLP_R2 are statistically significant.
Now since R1 is LP relaxation, it easily follows that
Theorem 5: 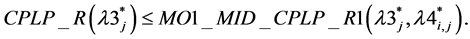
Conjecture 3: .
.
Conjecture 4: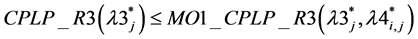 .
.
If only (15) is added to MID_CPLP then we get, MO2_MID_CPLP.
2.3.5. MO2_MID_CPLP
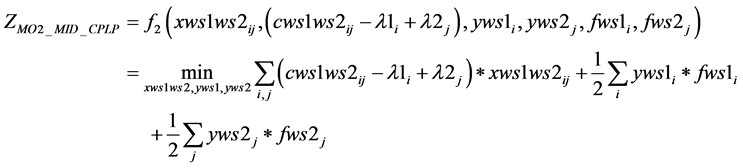 (1(q))
(1(q))
s.t.: (2(a)), (5(a-i)), (5(a-ii)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (8(b)), (9(b)), (10(b)), and (15).
Now we relax the constraints (5(a-ii)) and (15) by attaching multiplier 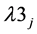 and
and 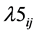 respectively to get the following.
respectively to get the following.
1) 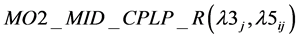
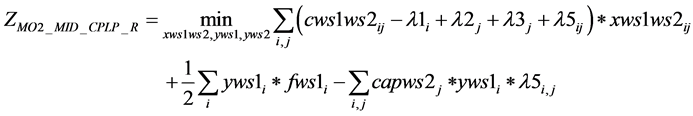 (1(r))
(1(r))
s.t.: (2(a)), (5(a-i)), (6(a-i)), (6(a-ii)), (7(a)), (8(a)), (9(a)), (10(a)), (10(b)).
2) 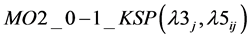
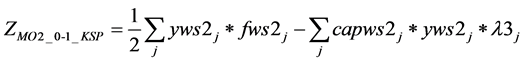 (1(s))
(1(s))
s.t.: (8(b)), (9(b)).
3) Relaxation of 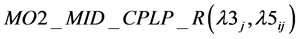
Now 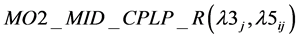 is attempted in literature by three different relaxations. They are R1, R2 and R3 respectively as before. When integrality restriction on yws1i is relaxed we obtain (12(a)).
is attempted in literature by three different relaxations. They are R1, R2 and R3 respectively as before. When integrality restriction on yws1i is relaxed we obtain (12(a)).
Result 9: we get,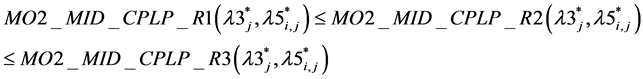 .
.
Theorem 6: For optimal value of ,
, .
.
Result 10: Differences between MO2_MID_CPLP_R2 and MO2_MID_CPLP_R1 & MO2_MID_CPLP_R3 and MO2_MID_CPLP_R2 are statistically significant.
Now since R1 is LP relaxation, it easily follows that Theorem 7: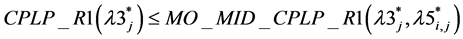 .
.
Conjecture 5: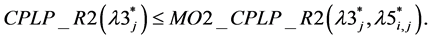 .
.
Conjecture 6: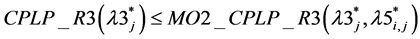 .
.
By the similar logic we have Theorem 8: we have, .
.
Theorem 9: we have,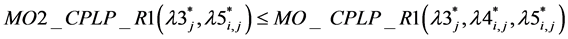 .
.
Now we give two more conjectures that are based on similar logic given earlier.
Conjecture 7: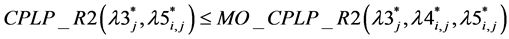 .
.
Conjecture 8: 
Since the effect of λ4ij and λ5ij is known only after it is through two combinatorial optimization problems, we believe a priori that it will difficult theoretically to prove the conjectures given in this paper. Hence we propose to carryout empirical investigation to support these conjectures.
3. Empirical Investigation and Statistical Significance
We have created sample problems randomly for the TSCWLP problem of sizes 25 × 25 × 25, 50 × 50 × 50, 75 × 75 × 75, and 100 × 100 × 100: CPLP_R1, CPLP_R2, CPLP_R3 and KSP; MO_CPLP_R1, MO_CPLP_R2, MO_CPLP_R3 and MO_KSP; MO1_CPLP_R1, MO1_CPLP_R2, MO1_CPLP_R3 and MO1_KSP; MO2_CPLP_R1, MO2_CPLP_R2, MO2_CPLP_R3 and MO2_KSP for the different values of θ such as 2, 1.6 and 1.2. For each category of the problem size we created 25 problems for fws1(i): 111-999, fws2(j): 111-999, capws1(i): 0.111-0.999 such that sum capws1(i) ≥ 1, capws2(j): 0.111-0.999 such that sum capws2(j) ≥ 1, cws1ws2(i,j): 1111-9999, thus created 3600 problem instances. We used the CPLEX 12.4.0.0 solver of GAMS 23.8 on an Intel (R) Core (TM) i7 CPU 870@ 2.93GHz and 4 GB RAM, 64 bit operating system to solve the problem instances. For each problem categories, we applied Lagrangian relaxations. Here, we obtained after Lagrangian Relaxation CPLP_R: Objective Function value of CPLP_R, KSP: Objective Function value of 0-1 Knapsack, MID_CPLP_R: Objective Function value of MID_CPLP_R, for each type of relaxations for R1, R2 and R3. Similar details for MO, MO1 and MO2 for R1, R2 and R3 can be written. Here, we only concentrate upon the objective function values of CPLP_R, KSP and MID_CPLP_R by applying Lagrangian Relaxations on the different formulations. After taking maximum objective function values of CPLP_R, KSP and MID_ CPLP_R for the different values of θ (denoted by *) for each category. The results of statistical significance are reported in the Table 1, Table 2, Table 3 and Table 4. In Table 5, standard t-critical values are given for n = 25, df = 24. Table 6 is giving all the information about empirical investigation.
4. Conclusion
Here we attempt problem TSCWLP by vertical decomposition. When the flow balance equations are relaxed, it leads to three versions of CPLP; that is, RHS_CPLP, LHS_CPLP and MID_CPLP. RHS_CPLP has been solved by Cornuejol, Sridharan and Thizy [14] and LHS_CPLP has been solved by Verma and Sharma [5] . We solve MID_CPLP again by LR and give interesting theoretical results; and these were mostly verified by empirical
Table 1. T-stat values for difference in performance of Lagrangian Relaxations on Model(j) - Model(i).
***Significant at 0.005 level, **Significant at 0.05 level, *Significant at 0.10 level. CPLP_R1*, CPLP_R2*, CPLP_R3*, (CPLP_R1+KSP_R1)*, (CPLP_R2+KSP_R2)* and (CPLP_R3+KSP_R3)* are the maximum values of CPLP_R1, CPLP_R2, CPLP_R3, (CPLP_R1+KSP_R1), (CPLP_R2+KSP_R2) and (CPLP_R3+KSP_R3).
Table 2. T-stat values for difference in performance of Lagrangian Relaxations on Model(j) - Model(i).
***Significant at 0.005 level, **Significant at 0.05 level, *Significant at 0.10 level. CPLP_R1*, CPLP_R2*, CPLP_R3*, (CPLP_R1+KSP_R1)*, (CPLP_R2+KSP_R2)* and (CPLP_R3+KSP_R3)* are the maximum values of CPLP_R1, CPLP_R2, CPLP_R3, (CPLP_R1+KSP_R1), (CPLP_R2+KSP_R2) and (CPLP_R3+KSP_R3).
Table 3. T-stat values for difference in performance of Lagrangian Relaxations on Model(j) - Model(i).
***Significant at 0.005 level, **Significant at 0.05 level, *Significant at 0.10 level. CPLP_R1*, CPLP_R2*, CPLP_R3*, (CPLP_R1+KSP_R1)*, (CPLP_R2+KSP_R2)* and (CPLP_R3+KSP_R3)* are the maximum values of CPLP_R1, CPLP_R2, CPLP_R3, (CPLP_R1+KSP_R1), (CPLP_R2+KSP_R2) and (CPLP_R3+KSP_R3).
Table 4. T-stat values for difference in performance of Lagrangian Relaxations on Model(j) - Model(i).
***Significant at 0.005 level, **Significant at 0.05 level, *Significant at 0.10 level. CPLP_R1*, CPLP_R2*, CPLP_R3*, (CPLP_R1+KSP_R1)*, (CPLP_R2+KSP_R2)* and (CPLP_R3+KSP_R3)* are the maximum values of CPLP_R1, CPLP_R2, CPLP_R3, (CPLP_R1+KSP_R1), (CPLP_R2+KSP_R2) and (CPLP_R3+KSP_R3).
Table 5. n = 25; df = 24; t table of critical values.
Table 6. Results, theorems, conjectures.
investigation. Theoretical results say that R1 < R2 < R3 in general; but in some cases this was not observed (as found by Verma and Sharma [5] ).
References
- Verma, P. and Sharma, R.R.K. (2008) Two Stage Capacitated Warehouse Location Problem: Conceptual Scheme of the Vertical Decomposition Approach. Proceedings of the 4th International Conference on Logistics and Supply Chain Management 2008, PSG College of Technology Coimbatore and Central Michigan University, USA.
- Geoffrion, A.M. and Graves, G.W. (1974) Multicommodity Distribution System Design by Benders Decomposition. Management Science, 20, 822-844. http://dx.doi.org/10.1287/mnsc.20.5.822
- Sharma, R.R.K. (1991) Modeling a Fertilizer Distribution System. European Journal of Operational Research, 51, 24- 34. http://www.sciencedirect.com/science/article/pii/037722179190142I http://dx.doi.org/10.1016/0377-2217(91)90142-I
- Sharma, R.R.K. and Berry, V. (2007) Developing New Formulations and Relaxations of Single Stage Capacitated Warehouse Location Problem (SSCWLP): Empirical Investigation for Assessing Relative Strengths and Computational Effort. European Journal of Operational Research, 177, 803-812. http://www.sciencedirect.com/science/article/pii/S037722170600018X http://dx.doi.org/10.1016/j.ejor.2005.11.028
- Verma, P. and Sharma, R.R.K. (2011) Vertical Decomposition Approach to Solve Single Stage Capacitated Warehouse Location Problem (SSCWLP). American Journal of Operations Research, 1, 100-117. http://www.scirp.org/journal/PaperInformation.aspx?paperID=7698#.U01DvHbedk4 http://dx.doi.org/10.4236/ajor.2011.13013
- Sahin, G. and Sural, H. (2007) A Review of Hierarchical Facility Location Models. Computers and Operations Research, 34, 2310-2331. http://www.sciencedirect.com/science/article/pii/S0305054805002959 http://dx.doi.org/10.1016/j.cor.2005.09.005
- ReVelle, C.S. and Eiselt, H.A. (2005) Location Analysis: A Synthesis and Survey. European Journal of Operational Research, 165, 1-19. http://www.sciencedirect.com/science/article/pii/S0377221704002139
- ReVelle, C.S., Eiselt, H.A. and Daskin, M.S. (2008) A Bibliography for Some Fundamental Problem Categories in Discrete Location Science. European Journal of Operational Research, 184, 817-848. http://www.sciencedirect.com/science/article/pii/S037722170700080X
- Brandeau, M.L. and Chiu, S.S. (1989) An Overview of Representative Problems in Location Research. Management Science, 35, 645-674. http://pubsonline.informs.org/doi/abs/10.1287/mnsc.35.6.645 http://dx.doi.org/10.1287/mnsc.35.6.645
- Sharma, R.R.K. (1996) Chapter 5. Foodgrains Distribution in the Indian Context: An Operational Study. In: Tripathy, A. and Rosenhead, J., Eds., Operations Research for Development, New Age International Publishers, Ahmedabad, New Delhi, 212-227.
- Sharma, R.R.K. and Namdeo, S. (2005) Two Stage Capacitated Warehouse Location Problem: Developing New Strong Constraints. Proceedings of 5th International Conference on Operational Research for Development: ICORD V, Jamshedpur, Jamshedpur, 19-21 December 2005, 330-333.
- Sharma, R.R.K. and Sharma, K.D. (2000) A New Dual Based Procedure for the Transportation Problem. European Journal of Operational Research, 122, 611-624. http://www.sciencedirect.com/science/article/pii/S0377221799000818 http://dx.doi.org/10.1016/S0377-2217(99)00081-8
- Verma, P. and Sharma, R.R.K. ( 2007) Vertical Decomposition Approach to Solve Single Stage Capacitated Warehouse Location Problems. Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 2-4 December 2007, 907-911. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4419323&tag=1
- Cornuejols, G., Sridharan, R. and Thizy, J.M. (1991) A Comparison of Heuristics and Relaxations for the Capacitated Plant Location Problem. European Journal of Operational Research, 50, 280-297. http://www.sciencedirect.com/science/article/pii/037722179190261S http://dx.doi.org/10.1016/0377-2217(91)90261-S
- Christofides, N. and Beasley, J.E. (1983) Extensions to a Lagrangean Relaxation Approach for the Capacitated Warehouse Location Problem. European Journal of Operational Research, 12, 19-28. http://www.sciencedirect.com/science/article/pii/0377221783901790 http://dx.doi.org/10.1016/0377-2217(83)90179-0
- Nauss, R.M. (1978) An Improved Algorithm for Capacitated Plant Location Problem. Journal of Operational Research Society, 29, 1195-1201. http://www.palgrave-journals.com/jors/journal/v29/n12/abs/jors1978263a.html http://dx.doi.org/10.1057/jors.1978.263


