ABSTRACT

Received December 7, 2013; revised January 7, 2014; accepted January 14, 2014

The application of some MVS operations (each dimension of which corresponds to a capability indicator) in sys- tem capability analysis and design, including capability indicator requirement analysis, effectiveness analysis, sensibility analysis, fuzzy analysis, stability analysis, capability optimization design, etc., is discussed in the second paper of this series of papers. And some MVS-based models and algorithms for capability analysis and design are put forward. Finally, an example of capability analysis and optimization design is given for explaining the usages of related models and algorithms.

Keywords:

Monotonic Vector Space; System Capability Indicators; Analysis; Optimization Design

1. Introduction

System capability indicator analysis and design are very important and also difficult for system development and system engineering. Many practical methods have been proposed and will be introduced in the following.

1.1. The Representative System Capability Indicator Analysis Methods

・ Index method. It is a traditional method for weapon system capability indicator analysis. This method is suit- able for synthesis and easy to understood. However, the index formula and weight influenced by analyzer are difficult to be determined. And the analysis result of index method is to some extent ambiguous.

・ ADC model [1]. Based on the principle of division and transformation of system state, this method proposed by WEISIC is able to give clear quantitative analysis result. However, the calculation overload will exponen- tially grow with the increasing of system dimension number. Furthermore, other models and algorithms are required to get the capability vector C of ADC model.

・ Weight-based multi-attributes analysis method [2,3]. This type of method such as AHP [4], ELECTRE, LINAMP, etc., determines weight of each indicator firstly. Then, all indicators are synthesized according to each of their weights in a linear way. Obviously, they are regardless of the mutual influence among indicators and so fail to reveal the nonlinearity of complex system. And furthermore their analysis results are also unclear.

・ SEA method [5]. This method compares system capabilities with mission requirements in a common attribute space and emphasizes the whole characteristic of complex system. This comparison leads to the evaluation of partial measures of effectiveness that are then combined to yield a global measure. But system mission requirement loci used by this method are difficult to acquire.

1.2. System Capability Indicator Design Method

・ Linera programming methods. This kind of method is traditional and neat. Many complex problems (espe- cialy with nolineartity and uncertainty) have to be over trivialized so as to be solved by these neat methods. Therefore, these methods are not directly effective for many complex problems.

・ Capability-based Planning (CPB) [6]. CPB method emphasizes the flexibility, adaptiveness and robustness of capability and usually adopts exploratory analysis strategy. Compared with programming method, CPB, as a flexible and non-neat method, is more suitable for complex problems.

Monotonic vector space (MVS) model is used for system capability indicator analysis and design in this paper. Since each dimension of MVS corresponds to one capability indicator, the MVS, therefore, is also called Mo- notonic Indicator Space (MIS) here. And likewise there exist some monotonic mappings between capability in- dicators and requirement measures in MIS.

1.3. Assumptions Adopted in This Paper

A monotonic relationship between the system capability indicators and the system requirement measures is assumed in this paper. It must be noted that system capability indicators are different from system parameters. For example, the velocity of a certain aircraft is not a capability indicator, but the maximal (or minimal) velocity of the aircraft is a system capability indicator. This assumption is usually in accordance with the practical situation in many cases. For example, in reference [5], there exists a monotonic relationship between the capability indi- cators (including reliability indicator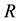, survivability indicator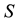, delay time indicator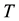, and link capacity indicator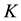) and the requirement measure, i.e. the ratio of kill to loss. In reference [7], there also exists a mo- notonic relationship between the capability indicators (including link reliability indicator and delay time indicator) and the requirement measure (the kill probability). Actually, similar monotonic relationship between the capability indicators and the requirement measure can be found in many practical cases introduced by references [8-12].

In addition, the weak capability is assumed to be a subset of the stronger one. Thus, if a system with weak capability meets some certain mission requirements, the one with stronger capability will be certain to meet these mission requirements. For example, if an aircraft with the maximal cruise velocity of 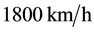can ar- rive at a certain location in one hour (a requirement measure), the one with maximal cruise velocity of 3000 km/h will definitely be able to arrive at the same location in one hour as long as the other capability indicators of these two aircrafts are equal.

The contents of system capability indicator analysis and design based on MIS include indicator requirement analysis, effectiveness analysis, sensitivity analysis, fuzzy analysis, relativity analysis, finance-based optimiza- tion design and time-based optimization design. The mutual relationships among these contents are shown in Figure 1. Obviously, system indicator analysis is the start point of system capability indicator analysis and de- sign. And in the following sections, the related models and algorithms for system capability indicator analysis and design will be dealt with in detail.

2. MIS-Based System Capability Indicator Analysis

2.1. System Capability Indicator Requirement Analysis

The partitioning operation in MVS introduced by the first part of this series paper is used to produce the system capability requirement locus. For example, the dimensions of a monotonic indicator space 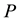for a ground-to-air missile system may include the searching radar detecting capability indicator dimension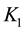, delay time indicator dimension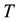, and tracking radar detecting capability indicator dimension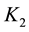. So, the equation

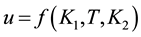describes the relationship between these three system capability indicators (i.e., 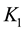, , 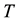and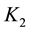) and one requirement measure 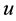(the kill probability). The function 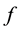may adopt several different forms, each of which corresponds to a different context. For example, 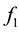and 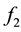correspond to the different contexts in which the enemy stealth aircraft is respectively type A and type B. Function 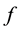is obviously monotonic, that is to say, the value of u (the kill probability) will monotonically increase or decrease with one of three system capability indicators changing monotonically while the others maintaining to be constants. Because the mono- tonic relationship between capability indicators (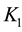and) and the requirement measure (the kill probability) is different from that between capability indicator and the kill probability, so, and are called monotonic increasing indicators and called monotonic decreasing indicator.

Every dimension in MIS can be continuous or discrete type. System capability indicators are usually of con- tinuous type as all the above mentioned ones. For discrete-type indicators, if its range is large enough, it still can be considered as continuous type just like many integer programming problems can be solved by general linear programming model. In this paper, all the dimensions of MIS are assumed to be continuous. The purpose of system capability indicator requirement analysis is to find out the MVRL or MIRL (monotonic indicator re- quirement locus) which can then be acquired with the algorithm proposed by the first part of this series papers. Figure 2 shows the MIRL for the above-mentioned ground-to-air missile system. There are 3 MIS dimensions, each of which corresponds to a capability indicator. The requirement measure (the kill probability for enemy invading stealth aircraft of type A and type B) is assumed as. The simulation calculation realizes the mapping from capability indicators to requirement measure. The MIRLs are produced by the partitioning algo- rithm at first and then synthesizing operation is used to produce the intersection of these multiple MIRLs which correspond to multiple requirements. According to the algorithm for producing MIRL, the algorithm output is a heap tree consisting of MIHs and MEHs. The MIHs compose the MIRL.

2.2. Effectiveness Analysis for the Indicators of Stochastic Type

Due to the uncertainty of the system capability indicators, it is usually difficult to represent them precisely. So the probability distribution function is applied to represent the system capability indicators. We represent a sys- tem capability indicator with such equation as, where and respectively denote the ex- pected value and a stochastic variable. Furthermore, a union probability density function where is the vector in the MIS is used to describe the system capability indicators. The system effectiveness is denoted as

and its expression is, where is the MIRL. It can be easily known that the range of

is. As the system effectiveness, reflects the extent to which system meets the requirements. If the

MIRL is approximated by the hyperboxes, i.e., where is the jth hyperbox and is the number of hyperboxes, the expression of will change into.

2.3. Sensitivity and Relativity Analysis for the Indicators of Stochastic Type

The purpose of getting the indicator’s sensitivity includes: 1) acquire the weightiness of indicator and determine

which indicator is critical; 2) more carefully deal with the uncertain and sensitive context or system capability indicators; and 3) optimize system.

The sensitivity analysis is realized by the perturbation analysis. This paper uses the analytic method to acquire the indicator’s sensitivity. In addition, every indicator is normalized within a common range for simplicity.

Definition 1. Denote the sensitivity of indicator as and its definition is

,

where and is the expected value of the system capability indicator (stochastic variable)

and also the perturbation variable.

Definition 2. Denote the relativity between indicator and as.

If;

If;

Definition 3. Possibility measure [13]. is assumed as a non-empty set and as the power set of.

If meets three axioms, i.e., , , and, it is

called possibility measure.

Definition 4. System effectiveness based on the fuzzy indicators and possibility measure. The ex- pression of is, where is multi-dimensional fuzzy indicator and is the re- quirement locus. The value of can be acquired by fuzzy simulation method which is detailed as follows.

Step 1 Set and is a very small estimate of.

Step 2 According to subordinating fuction of, uniformly produce from set and let.

Step 3 Set.

Step 4 If and, set

Step 5 Repeat step 2 to 4 times.

Step 6 If, return.

Credibility, which reveals the possibility and impossibility simultaneously, is a novel mode describing fuzzy relation. So, as a measure, credibility is more reasonable than possibility. The definition of credibility measure is stated as follows.

Definition 5. Credibility measure [13]. With the assumption that is a possibility space and is the element of power set, credibility measure is defined as

.

Definition 6. System effectiveness based on the fuzzy indicators and credibility measure. The ex-

pression of can be stated as, where is multi-

dimensional fuzzy indicator and is the requirement locus. Similarly, it can be acquired by fuzzy simulation method.

Step 1 Uniformly produce from and let if, where is a very small number.

Step 2 Let

and then return.

For the above two algorithms, it is important to judge whether the is within or not. And based on the tree structure output of partitioning algorithms introduced in the first one of this series papers, it can be quickly judged whether the is within or not. The judging procedure is detailed as follows. Firstly, judge whether the is within the top MEH (root of the tree) or not. If it is not, it is not within either and the judging procedure ends. If is within the MEH, judge whether is within the next-level MIH or not. If is within the MIH, it is also within and the judging procedure ends. If it is not, judge whether is within one certain MEH of this level or not. If is contained by one MEH, continue the recursive searching proce- dure from this MEH. If searching reaches the bottom of the tree and no one MIH containing is found, it means that this is not within.

2.4. Effectiveness Analysis Based on Fuzzy MIRL

Definition 7. Fuzzy monotonic indicator requirement locus (FMIRL). is a fuzzy set on a cer- tain domain; is the l-cut set of; and is the effective range in P (MIS) which meets the re- quirement. These concepts are now illustrated by an example. For an air defense system, the mission re- quirement measure (fuzzy set) is killing the enemy aircraft. The domain is the kill probability. Set a l to de- termine the. is a requirement measure of kill probability that must be larger than a certain value.

The fuzzy system capability indicator (assumed to be stochastic) effectiveness analysis model is introduced as follows. can be determined according to l. If, we can get the corresponding conclusion, i.e., and according to the monotonic assumption.

and;

when. So,. And can be solved rapidly by

the binary method. The fuzzy effectiveness analysis model is not only suitable for the fuzzy requirement but also able to decrease misclassification rate of the boundary points especially when the system capability indicator values are distributed near the boundary of MIRL.

3. MIS-Based System Capability Indicator Optimization Design

3.1. Budget-Oriented Optimization Design

Budget-oriented capability indicator optimization design will be discussed in this section. In order to make a system meet a certain requirement, there are usually many development “paths” with different cost for system capability indicators. Figure 3 gives three linking paths (i.e., OA, OB and OC) between point O representing the initial system capability and the requirement locus. And point O is assumed to be out of the requirement locus. Certainly, besides these three paths, there exist countless other linking paths between point O and requirement locus. The purpose of capability indicator optimization design is to find out the path with the minimal budget or least time cost. In this paper, the optimization model is used to get the optimized expectation values of the statis- tical capability indicators according to practical problems. For simplicity, all the capability indicators are as- sumed to be mutually independent and have fixed variances (i.e., every capability indicator can be developed independently). And the optimization design model is:

In this model: is union probability density function and, as the optimization variable, repre-

sents the expectation value of;, , and respectively represent the MIRL (monotonic indicators requirement locus), the effectiveness value, and the capability indicator effectiveness requirement threshold; represents the budget-cost function of capability indicator varying from to. The which meets the effectiveness requirement and has the least budget can be found through optimization. The corresponding duality programming is

.

This model will be used to get the maximized capability indicator effectiveness value with the budget being less than.

3.2. Time-Oriented Optimization Design

Capability development is usually a time-consuming work. The following optimization model is able to find the path from the original capability point to MIRL with the least time.

.

In this model: represents time-cost function of the capability indicator varying from to and represents the total number of capability indicators. This model can also be transformed into the following programming model,

.

Similarly, the dual programming can be changed into

.

4. A Notional Example: Number Optimization of Missiles Available

In this section, some models and algorithms mentioned above are used to program missile available numbers of six types so as to meet the mission requirement with the least budget cost.

4.1. Problem Context

Ten types of opponent targets (i.e., T1, T2, T3, T4, T5, T6, T7, T8, T9, and T10) are assumed to be destroyed to win the air superiority. Target-attacking missile types are assumed to be type A, type B, type C, type D, type E, and type F.

Because missile production cost is usually very large, so the missile number available of each type is an im- portant capability indicator. The capability indicator optimization design will be carried out in a MIS with six dimensions (i.e., six missile available number indicators). The required number of one certain type missile, when only this type of missile is used to destroy one target of a certain type, is presented in the following table. “No” in the table means that type of missile can not be assigned to attack the corresponding type of target.

If there exists solution meeting the following equality and inequalities group, it means that the missile number available of each type can satisfy the mission requirement.

In the above equation and inequalities group, , , and respectively represent the number of the type of missile assigned to the type of target, the required number of the type missile to destroy type target, and the number available of type missile.

If the number available of each type of missiles all meet the mission, the requirement measure is set to 1, otherwise, set to 0. And the function is obviously monotonic.

4.2. Capability Indicator Analysis and Optimization Design

The MIS-based capability indicator analysis and optimization design is performed according to the following steps.

1) Construct the MIS, i.e., select all the MIS dimensions and standardize every dimension value range into the range [0,100].

2) Create the monotonic function representing the relation between the capability indicators and requirement measure. Actually, the function is already put forward in section 4.1.

3) Apply the partitioning algorithm to acquire the MIRL, i.e., accomplish capability indicators requirement analysis.

4) Use the capability indicators effectiveness model (introduced in section 2.2) to judge whether the present capability meet the requirement or not. If not, go to step5 to perform optimization design, else stop capability indicator analysis and optimization design.

5) Trade off missile number for each type with the optimization model introduced in section 3.1.

Based on the data of Table 1, the MIRL shown in Figure 4 is acquired by the partitioning algorithm. The numbers of six types of missiles (i.e., type A, B, C, D, E, and F) available is respectively assumed to be 14 - 26 number unit, 14 - 26 number unit, 12 - 29 number unit, 14 - 26 number unit, 14 - 26 number unit, and 12 - 29 number unit.

All the numbers of six types of missiles available are assumed to be subject to normal distribution and according to principle, the corresponding distribution functions can be approximately stated as follows:

Furthermore, the budget costs of six types of incremental missiles are assumed to be evaluated with the fol- lowing functions:

;;;

;;.

In these functions: respectively represent the incremental missile numbers of the type A, B, C, D, E, and F; respectively represent the budget costs of the incremental missiles of type A, B, C, D, E, and F.

If the effectiveness value (introduced in section 2.2) is required to be larger than 0.9, the optimized in- cremental numbers of six types of missiles can be acquired through conducting the following programming model.

In this model:

respectively represent the probability density functions of missile numbers of type A, B, C, D, E, and F; respectively represent the expectation values of six distribution functions; respectively represent the incremental missile numbers of type A, B, C, D, E, and F. The initial numbers of six types of missiles are all and variances of six distribu- tion functions are 2 or 3.

Through solving the programming model mentioned above, we get such conclusions that the optimized in- cremental missile numbers of type A, B, C, D, E, and F should be 28 number unit, 28.2 number unit, 27.9 num- ber unit, 25.7 number unit, 36.5 number unit, and 35.9 number unit and the optimized least budget cost will be 3275 (cost unit).

5. Conclusion and Perspective

This series of papers propose and introduce a novel model, i.e., MVS (monotonic vector space) model, in which there exist some monotonic mappings. Many MVS operations (such as partitioning operation, synthesizing op- eration, sampling operation, etc.) can be directly used to solve related practical problems, which have been ela- borated in the first one of this series papers. Based on MVS, some system capability indicator analysis and op- timization models (e.g., requirement analysis model and effectiveness analysis model) are put forward and used to perform capability indicator analysis and optimization design in the second one of this series of papers. The future work for MVS model includes: 1) improving the present operation algorithms and developing other types of operations (such as partitioning operation in non-deterministic discrete or non-deterministic continuous MVS), which is of great significance to practical problems; 2) extending the application of the MVS model in other fields such as imaging processing and multi-object programming, etc.

Funding

Supported by NSFC, China, PRC, Grant No 70871120.

References