 Journal of Power and Energy Engineering, 2014, 2, 162-169 Published Online September 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.29023 How to cite this paper: Xia, C.J., Zhou, Y., Men, K. and Xie, Y.G. (2014) Study on Identification of Inductive-Motors Load Par- tition Based on Coherence. Journal of Power and Energy Engineering, 2, 162-169. http://dx.doi.org/10.4236/jpee.2014.29023 Study on Identification of Inductive-Motors Load Partition Based on Coherence Chengjun Xia1, Yun Zhou1, Kun Men2, Yinggeng Xie1 1School of Electric Power, South China University of Technology, Guangzhou, China 2Electric Power Research Institute of CSG, China Southern Power Grid, Guangzhou, China Email: yunzh09@163.com Received June 2014 Abstract A new inductive motors load equivalence algorithm based on coherence is proposed in this paper. In order to partite motors load rapidly and accurately, fuzzy c-means clustering along with parti- cle swarm optimization (PSO-FCM) algorithm is proposed to identify coherent motors base on its physical essence of fuzziness. The merits of PSO algorithm are independent to initial value and convergent to optimum value rapidly, and the validity function is constructed to assess clustering validity. The test on IEEE 39-Bus System is presented to evaluate the effectiveness of the new algo- rithm, the membership matrix definite not only coherence group of motors but also correlation value of coherence between motors. The algorithm can be used to partite motor load based on co- herency in dynamic equivalence with power system operating on different modes. Keywords Load Model, Inductive-Motor Load, PSO, FCM, Clustering Validity, Dynamic Equivalent 1. Introduction To simplify the analysis of the large scale interconnected power system, a series of power system equivalent methods had been proposed in recent years. Numerous investigations had shown that the load model has an im- portant and complex role on the dynamic simulation and response of power system after fault. Because most power system loads involve many inductive motors, it makes sense to develop an effective identification theory for industrial loads which comprised of different induction motors. In order to obtain more accurate results in transient analysis and simulation, it is necessary to identify inductive motors based on coherence [1]-[3]. For actual power system, there is no coherence load in the strict sense because of the uncertainty of load model. The similar dynamic characteristics exist in coherence load due to its ambiguity. In [4], clustering me- thod is used to partite motor load, and criteria of coherence were proposed in dynamic control and analysis in power system. In [5], dynamic performance of power system load representation is analyzed and the importance of load modeling is emphasized. In [6], the identifiability of the equivalent motor parameters is investigated in the composite load model, case studies verify the validity of the proposed method. This paper proposes a method for the identification of inductive motors load partition based on coherence. In order to partite motors load rapidly and accurately, fuzzy c-means clustering along with particle swarm optimi-  C. J. Xia et al. zation (PSO-FCM) algorithm is applied to identify coherent motors base on its physical essence of fuzziness. Then fuzzy partition entropy function is used as a measurement index to measure the performance of algorithm and evaluate the effectiveness of fuzzy c-mean clustering algorithm based on particle swarm optimization. The computational results show that control strategy works effectively and can be applicable to the identification problem. 2. Load Models in Power System 2.1. Static Load Models [7] The load models are traditionally classified into two broad categories: static models and dynamic models. A static load model expresses the characteristics of the load at any instant of time as algebraic functions of the bus voltage magnitude and frequency at that instant, including ZIP model, exponential model and polynomial model. An alternative model which has been widely used to represent the voltage dependency of loads is the ZIP model, as it is composed of constant impedance (Z), constant current (I), and constant power (P) components. 2.2. Dynamic Load Models There are, howev er, many cases where it is necessary to account for the dynamic of load components. Studied of inter-area oscillations, voltage stability, and long-term stability often require load dynamics to be modeled. Study of system with large concentrations of motors also requires representation of load dynamics. The dynamic characteristics of induction machine should be taken in account in terms of influence of induc- tion machine on power system. The dynamic equation of an induction machine may be written as: 0 0 1 =-[-(X -X )]-(-1)E 1 =-[-(X -X )]-(-1)E ddq brq qqdbrd dE EI dt T dE EI dt T ωω ωω ′ ′′ ′ ′ ′ ′′ ′ ′ (1 ) 22 22 1 =[(V -E)+(-E)] + 1 =[(V -E)-(-E)] + dsdd qq s qsqq dd s IR XV RX IRXV RX ′′ ′ ′ ′′ ′ ′ (2) (3) where, and are transient electric potential, is rotor angular velocity, , , , ; TJ is motor inertia time constant, S is slip speed of rotor. is me- chanical torque, is electromagnetic torque; is rotor open circuit reactance. 2.3. Synthesis Load Model For actual power system, the modeling of loads is complicated because a typical bus represented in stability studies is composed of a large number of devices. The exact composition of load is difficult to estimate. The characteristics of load can be represented by the ZIP models and induction machine. The synthesis load model consists of third-order induction motor in paralleled with ZIP. The schematic structure of this synthesis load model is shown in Figure 1. In Figure 1, Rs is stator equivalence resistance, Xs is stator equivalence leak reactance, Rr is rotor equivalence resistance, Xr is rotor equivalence leak reactance, Xm is value of mutual inductance between stator and rotor windings. Model order reduction techniques are often used to reduce the model complexity. When analyzing the tran- sients of circuits and electrical machines, the detailed model is often built first to describe the plant as accurately as possible. Then the model order can be reduced according to the specific problems under investigation.  C. J. Xia et al. Figure 1. Equivalent circuit of the synthesis load model. 3. The Characteristics for Load Partition Identification The dynamic characteristics of equivalence load will be poor in the circumstance because there are amount of discrepant load in equivalence load. To guarantee the accuracy of dynamic simulation of power syste m, it’s necessary to partite load in appropriate way [8]. The essence of partition equivalence load is to observe the dynamic characteristics of aggregation load. For induction machine, the best tool to study the performance is slip. The relationship between slip and rotor speed is s = (n0−n)/n0, so s is corresponding to speed completely. If Tm is constant, the formula of Te can be expressed as following: (4) where, Scr = Rr/Xl is critical slip, Xl is sum of rotor leak reactance and stator leak reactance. Therefore, the lin- earized forms of Equation (4) is (5) 22 N2 2 -/ =+/ cr Ncr lcr Ncr Uss s Xsss ζ ⋅ (6) Generally, the value of SN is quite small, so compare to Scr, it can be ignored. Then, 222 1== NN lN l crlrr UU XU Xs XRR ζ ≈× × (7) Therefore, the linearized forms of Equation (7) is (8) From the given Equation (8), the corresponding solution is (9) So is determined by TJRr. If values of TJRr of the induction machine are similar, then they own similar dynamic characteristics. Finally, to evaluate the state of induction machine, (TJRr, KL) is chosen to be a charac- teristic quantity which is used to identify coherence inductive motors in power system. So, coherent inductive motors own similar characteristic quantity. 4. Improved Fuzzy c-Means Clustering Algorithm 4.1. Fuzzy c- Means Clustering Fuzzy c-means clustering (FCM) approach is widely implemented to tackle practical problems with uncertainty,  C. J. Xia et al. imprecision and vague peculiarity. Initial categories and parameters are given before the program began to iter- ate. Satisfying solution for project can be obtained though modification, as well as iteration. Robust results for categories can be achieved based on fuzzy clustering. The formula of FCM can be expressed as following: 22 11 11 min=( ) NK NK mijijij ik ij ij Jux cu = == = = − ∑∑∑∑ d ( 10) where, xi is sample, cj is a set of class center, U = (uij) is a membership matrix of samples. To solve Equation (10) is impossible. Formula for soft clusters was given by mathematician Bezdek [9] [10]: 2 1 1 1 ij cm ij kik ud d − = = ∑ (11 ) (12) 1 2 2 1 d () m ijij kj j xc = = − ∑ (13) where, m is constant of vague degree, dij represents the distance between sample and class center. 4.2. Particle Swarm Optimization In PSO, the solution of the objective function can be imaged as a point in d-dimension, just as a bird fly in the sky. The process of finding the solution is based on the analogy of swarm of bird flocking and fish schooling. A swam of particles represent a candidate solution to the optimization problem [11] [12]. Each particle adjusts its position according to its own experience, and the experience of its neighbouring par- ticles. The position and velocity of the ith particle in the d-dimensional search space are represented in (14) and (15). (14) 1112 2 ()( ) kk ididid idgd id vvc randpxcrandpx ω += +−+− (15) where, Xik is position of individual i at iteration k, Vik is velocity of individual i at iteration k, is weight pa- rameter, c1 is cognitive factor, c2 is social factor, pid is the best position of individual i until iteration k, Pgd is the best position of the group until iteration k, rand1, rand2 are random numbers between 0 and 1. To evaluate the merit rating of the particles, we can set a function to measure which called the fitness function. According to the fitness function, the best particle is selected. And initial positions and velocities are vector. Particles can move to a better position by sensing its own position and the particles nearby. In every step each agent’s position is updated by the best fitness value called as pibest. Also each agent knows the best value in the group called as pgbest among the pibest. After a specified number of iterations, the agents searching points gradu- ally reach the global optimal point using pibest and pgbest. An inertia weight in PSO algorithm was introduced in 1998, in order to provide better control exploration [13]. The inertia weight is used to control the impact of the previous history of velocity, and thus to influence the tradeoff between global and local exploration abilities of the moving agents. In PSO, the balances between the global and local exploration abilities are mainly controlled by inertia weights. Both convergence speed and ac- curacy of solution will be affected. The inertia weight is suggested to decrease linearly from 0.9 to 0.4 during the run. The inertia weight is formulated as in (16). max max minmin min ( )() n Tt T ω ωωω ω − = −+ (16) 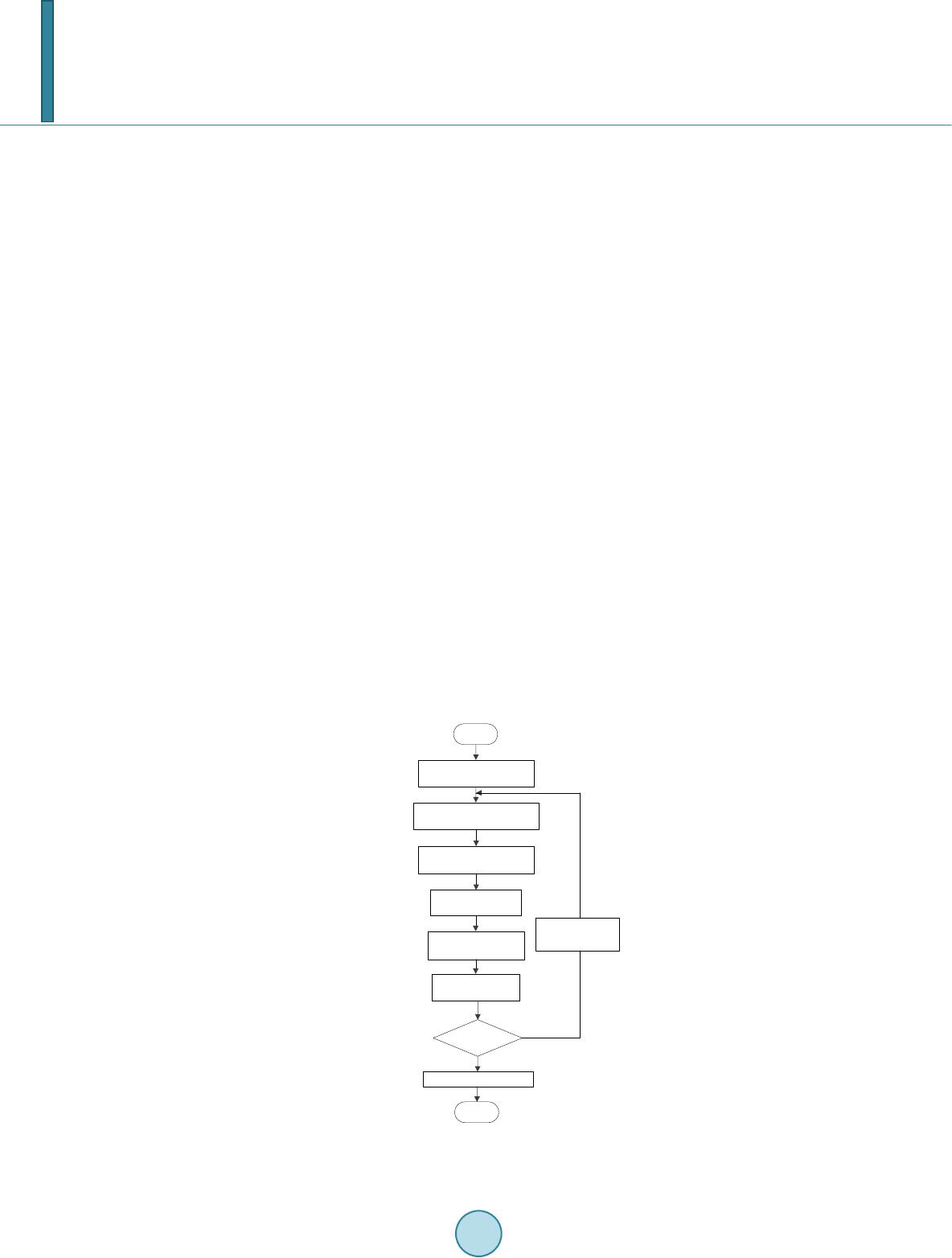 C. J. Xia et al. where is the attenuation index of inertia weight, is the initial value of the inertia weight, is the final value of the inertia weight, Tmax is the maximum iteration number; t is the current iteration number. 4.3. Particle Swarm Optimization Fuzzy c-Means Clustering Algorithm As fuzzy c-means algorithm is easy to convergent to partial optimum, PSO is introduced to program instead of the process based on gradient descent. The performance of the algorithm is fantastic and effective in the process of iteration, and it is insensitive to initial values. Finding the optimal particle center is main task in the process of iteration. Hence, class center ci is encoded as a particle. The particle can be expressed as following: () 1,1 1,,,1, ,...,,..., ,...,,..., lD ijKKD xc cccc = (17) where, cij is the center ith with clustering method jth. To evaluate the performance of particle, objective function is recommended. In the paper, JH is used to be ob- jective function to compare the performance among particles. The objective function can be expressed as fol- lowing: (1 8) Solving Equation (18), we can obtain the fitness for every particle. Particle optimum point can be obtained after comparing the global optimal point and particle optimal point. If f(xid) is greater than f(pgd), then fitness of global optimal point will be updat ed, vice versa. ( )( ) ( ) ( ) ( ) ()( ) ( ) ( ) ( ) ,1 1, 1 idid id id id id id f tft p xx t ptf tft pp x ≥− =− <− (1 9) The iteration structure of particle swarm optimization fuzzy c-means clustering algorithm is presented in Figure 2. 4.4. Evaluating the Effectiveness of Clustering Algorithm To evaluate the effectiveness of fuzzy c-mean clustering algorithm based on particle swarm optimization, fu z zy Set the initial parameters Randomize particles Calculate membership for clustering center as in (11) Calculate objective function as in (10) Calculate the fitness: fi as in (18) Update Pibest and Pgbest as in (19) Start |uijk+1-uijk|<ε Update the new Vi and Xi Out optimal parameters Yes No Stop Calculate clustering center as in (12) Figure 2. Block diagram of PSO-FCM algorithm.  C. J. Xia et al. partition entropy S(U,K) is used as a measurement index to measure the performance of algorithm. The small S(U,K) is, the dispersion degree between particle is smaller, that is to say, the performance of clustering algo- rithm is more perfect. S(U,K) can be expressed as: ( ) 2 2 11 2 , 1 ,min NK ij ij ij ij ij uxc N SUK cc = = − ∑∑ =− (20) The distance between clusters and the data points assigned to them should be minimized and the distance be- tween clusters should be maximized [14]. 5. Simulation and Numerical Analysis To verify the effectiveness of the proposed algorithm, source program is developed for identification of induc- tive-motors load partition based on coherence for simulations and is applied to the standard IEEE-39 bus benchmark system. The parameters used for chaos particle swarm optimization algorithm are as following: num- ber of particles is 30, , , number of iterations is itermax = 100, . Research system and external system are shown in Figure 3. Broken line passing through bus 39, bus 3 and bus 27 is shown in Figure 3. Taking actual research into consideration, research system is one above the broken line. The program is developed to partite the coherence motors in outside system including 13 motors. It is clearly known that clustering results with the relationship among membership matrix. The results of iden- tification of inductive-motors load partition based on coherence can be written as following. 2 Group: (3, 4, 7, 8, 12, 15, 18); (16, 20, 21, 23, 24, 27) 3 Group: (3, 4, 7, 8, 12, 15, 18); (16, 20, 21); (23, 24, 27) 4 Group: (3, 4, 7, 8, 12, 15, 18); (16, 20, 21); (23, 27); (24) The value of fuzzy partition entropy S(U,K) is shown in Table 1. Therefore, it can be inferred that the cluster performance is best in group 2. Optimum membership matrix U can be obtained after calculation and simulation. 0.0084 0.0006 0.0064 0.0033 0.0092 0.00060.9841 0.0033 0.9767 0.9609 0.9657 0.9870 0.9657 0.9916 0.9994 0.9936 0.9967 0.9908 0.99940.0159 0.9967 0.0232 0.0391 0.0343 0.0130 0.0343 U= For this improved PSO-FCM algorithm, the program runs after parameters initialized, and convergen ce re- sults of iteration are shown in Figure 4. GG G G G G GG GG 30 39 1 2 25 37 29 17 26 9 3 38 16 5 4 18 27 28 3624 35 22 21 20 34 23 19 33 10 11 13 14 15 831 12 6 32 7 Figure 3. Diagram of IEEE-39 with 10 generators.  C. J. Xia et al. The progress of PS O-FCM algorithm can be illustrated easily in Figure 4. After 35 times iteration, the task of iteration is over. And the optimum solution can be obtained. So identification of inductive motors load partition based on coherence can be easily implemented. To illustrate the stability of the proposed algorithm, source program is developed for identification of induc- tive motors load partition, and runs for several times, which contain 2 groups of inductive motors. The results are shown in Tab le 2. It is clearly know that the results are same nearly. The value of fuzzy partition entropy in iteration 3rd, 5th, 6th, 8th, and 10th is 7.7845e−04. The value in iteration 2nd, 7th is 7.7853e−04. The error existed between maximum and minimum is only 0.0034. It is sufficient to illustrate the stability of proposed algorithm. Considering convergence rate, the PSO-F CM method can always generate precipitous convergence rate to- ward an acceptable solution, wh i ch show that the PSO-FCM method has good convergence performance. As shown in Figure 5, the convergence characteristic from 20 to 30 times is different. The program based on PSO- FCM is easier to be convergent with certain reliability. And it can be applied to large-scale power systems. Table 1. The validity function value. Group 2 3 4 S(U,K) 7.7862e−004 0.0437 0.2261 Table 2. S(U,K) value of ten times simulation (e−004). Times 1 2 3 4 5 S(U,K) 7.7862 7.7853 7.7845 7.7879 7.7845 Times 6 7 8 9 10 S(U,K) 7.7845 7.7853 7.7845 7.7845 7.7845 010 20 30 40 50 60 70 80 90100 0.105 0.110 0.115 0.120 Fitness Value Iteration Figure 4. Fitness function evolution curve. 010 20 30 40 50 60 70 80 90100 0.105 0.110 0.115 0.120 0.125 Fitness Value Iteration Figure 5. Fitness function evolution curve in ten times.  C. J. Xia et al. 6. Conclusion To investigate the identification of inductive motors load partition based on coherence, PSO -FCM algorithm is proposed considering the characteristic of inductive motor load. The proposed algorithm uses PSO to find opti- mum instead of the process of gradient descent. The coherence motors can be identified according to member- ship matrix, as well as intensity of coherence motors. For the sake of validating the coherence motor in dynamic studies, a series of simulation tests are performed and compared. And the analysis results of measured simula- tion curves show that the coherence motors identified by the proposed strategy possess good description ability for load dynamics. What’s more, the proposed identification strategy can improve the stability of identification results, by which promotes the practical application of the load model. Case study also shows the effectiveness and feasibility of the proposed identification strategy. Acknowledgements This work was financially supported by National High Technology Research and Development Program of China (2012AA050209). References [1] Shenghu, L., Zhengkai, L., Xinjie, H. and Shusen, J. (2010) Dynamic Equivalence to Induction Generators and Wind Turbines for Power System Stability Analysi s . International Symposium on Power Electronics for Distributed Genera- tion Systems, Hefei, 16-18 June 2010, 887-892. [2] Baozhen, Z., Yao, Z., Qing, Z. and Zhaobin, D. (2011) Application of Dynamic Equivalence Based on Coherency in South China Power Grid. Power and Energy Engineering Conference, Wuhan, 25-28 March 2011, 1-4. [3] Resende, F.O., Matevosyan, J. and Milanovic, J.V. (2013) Application of Dynamic Equivalence Techniques to Derive Aggregated Models of Active Distribution Network Cells and Microgrids. PowerTech IEEE Grenoble, Grenoble, 16-20 June 2013, 1-6. [4] Haiqiang, Zh., Ping, J., Hui, Y. and Ran, S. (2010) Dynamic Equivalent Method of Interconnected Power Systems with Consideration of Motor Loads. Science China Technological Sciences, 40, 902-908. http://dx.doi.org/10.1007/s11431-010-0110-8 [5] He, R., Ma, J. and Hill, D.J. (2006) Composite Load Modeling via Measurement Approach. IEEE Transactions on Power Systems, 21, 663-672. http://dx.doi.org/10.1109/TPWRS.2006.873130 [6] Ma, J., Han, D. and He, R. (2007) Research on Identifiability of Equivalent Motor in Composite Load Model. Power Tech IEEE Lausanne, Lausanne, 1-5 July 2007, 1015-1020. [7] Kundur, P. (2001) Power System Stability and Control. 1st Edition, McGraw Hill Inc., New York. [8] Wang, J., Han, M. and Ma, J. (2010) A New Identification Strategy for Improving Convergence Stability of Load Model Parameters. International Conference on Electrical and Control Engineering, Wuhan, 25-27 June, 145-148. [9] Pal, N.R., Pal , K. and Keller, J.M . (2005) A Possibilistic Fuzzy c-Means Clustering Algorithm. IEEE Transactions on Fuzzy Systems, 13 , 2005. http://dx.doi.org/10.1109/TFUZZ.2004.840099 [10] Chunjuan, Y. (2011) Derivatives of Fuzzy C-Means Method and Their Application Comparisons. International Con- ference on Computer Science and Service System, Nanjing, 27-29 June 2011, 326-329. [11] Fengrui, Z., Jianshu, C. and Zhenhui, X. (2013) An Improved Particle Swarm Optimization Particle Filtering Algo- rithm. International Conference on Circuits and Systems, Chengdu, 15-17 November 2013, 173-177. [12] Lin, L., Qi, L ., Junyong, L. and Chuan, L. (2008) An Improved Particle Swarm Optimization Algorithm. IEEE Inter- national Conference on Granular Computing, Hangzhou, 26-28 August 2008, 486-490. [13] Yi, S., Yunfeng, B. and Mingxin, Y. (2009) A Novel Chaos Particle Swarm Optimization (PSO) and Its Application in Pavement Maintance Decision. IEEE Conference on Industrial Electronics and Applications, Xi’an, 25-27 May 2009, 3521-3526. [14] Lingkui, M. and Chunchun, H. (2007) Cluster Validity Index Based on Measure of Fuzzy Partition. Computer Engi- neering, 33, 15-17.
|