R. A. Leonidovich et al.
Concentrate consumption (kg/h)
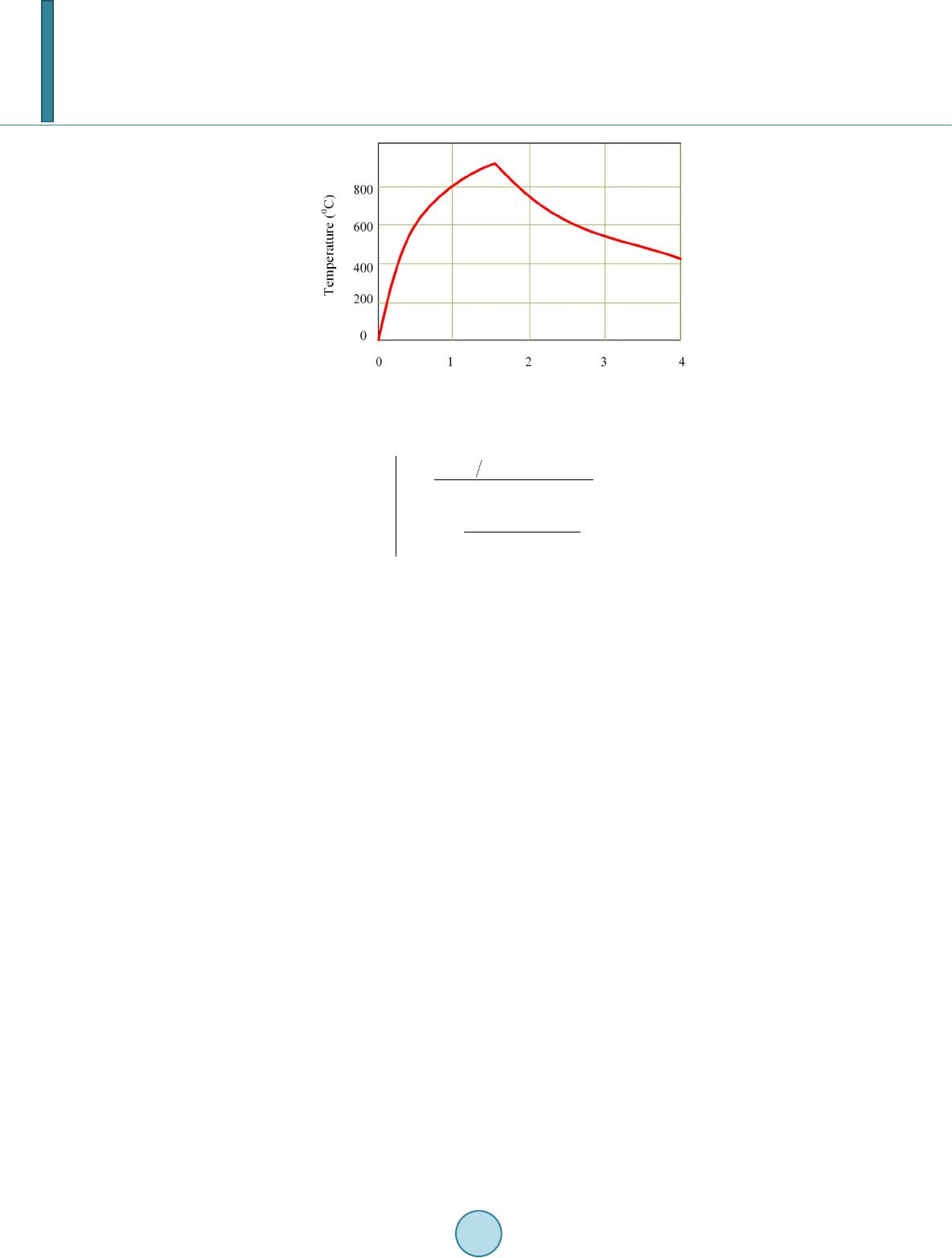
Figure 3. Dependence of the temperature of the boiling layer on
the concentrate consumption.
( )( )
()
v vc
v
2.991
vc vvv
ccv
c
cc vvv
ccv
Gq GсT
Tif GG
GGc
TG Gq GсT
T otherwise
GGc
⋅+ ⋅⋅
←≤
+⋅
=
⋅ +⋅⋅
←+⋅
(6)
Researchers conducted the calculating experiment using the Mathсad software and identified the dependence of
the boiling layer temperature on the concentrate consumption (Figure 3).
The sensitometric curve displays the extreme character of the dependence. The inf lu ence of the per tu rba tion
action on the dependence leads to th e shif t of the ex t remum and the rise of drift of the static characteristic.
Output parameter of the roasting pr oces s, temperature in the “fluidized bed” furnace, is defined by the amount
of the burned cinder and by the amount and temperature of the incoming air. The cinder does not burn completely
with the small amount of air, and this, therefore, reduces productivity of the process. With excess of air in the
“fluidized bed ” furnace, fuel of the furnace charge burns completely, but much of the heat released during its
combustion is used to heat the excess air and is carried away from the furnace with products of burning and excess
air.
At a certain ratio of the amount of cinder and incoming air, the temperature mode of the “fluidized bed” furnace
will be optimal corresponding to an extremum of the output parameter of the process.
At the optimum consumption of the concentrate, its full oxidation is provided, and the temperature reaches its
maximum. Consequently, the purpose of managing the roasting process is redu c ed to maintaining optimum per-
formance of the “fluidized bed” furnace operation, where in a continuous mode its maximum productivity is
reached with the change of conditions of conducting the process and limited aprioristic infor mation about it.
The process of roasting of zinc con centrates belon gs to in ertial control objects and is characterized by difficult
dynamics. Change of the key regime parameters of the proces s may lead to a drift of the position of th e optimum of
studied dependence. Consequently, provision and long-term maintenance of the optimum static mode of the
studied process may be realized based on the use of the extreme control systems. Stabilization of the process is
reduced to the repeated solution of the interconnected problems of defining the extreme position of the working
point and the organization of movement toward it.
References
[1] Rutkowki, A.L., Meshkov, E.I., Davidson, A.M., Zurabov, A.T. and Kovaleva, M.A. (2009) Investigation of the Proc-
ess of Jet Burning of Gaseous Fuel. Journal of Engineering Physics and Thermophysics, 82, 133-139.
[2] Rutkowski, A.L., Bigulov, A.V., Bilaonov, B.D. and Dzantiyev, N.L. (2013) Analysis of Regularities of Process of
Burning of Gaseous Fuel in a Torch Mathematical Modeling. Mining Informational and Analytical Bulletin (Scientific
and Technical journal), 2, 131-138.
[3] Salikhov, Z.G., Arunyants, G.G., Rutkowki, A.L. (2004) Systems of Optimum Control of Difficult Technological Ob-