 Journal of Power and Energy Engineering, 2014, 2, 29-34 Published Online September 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.29005 How to cite this paper: Shao, M.L., Liang, Q.C., Yan, D., Qin, H. and Xiang, J. (2014) Application of Fuzzy Comprehensive Evaluation on COGAG Power Plant of Performance. Journal of Power and Energy Engineering, 2, 29-34. http://dx.doi.org/10.4236/jpee.2014.29005 Application of Fuzzy Comprehensive Evaluation on COGAG Power Plant of Performance Menglin Shao1, Qianchao Liang1, Dong Yan1, Heng Qin2, Jun Xiang2 1The College of Naval, University of Engineering, Wuhan, China 2The DaLain Naval Vessel Academy, Dalian, China Email: smlin18@163.com Received May 2014 Abstract A fuzzy comprehensive evaluation of COGAG power plant performance is given by using a method of fuzzy mathematics, and multilevel fuzzy evaluation model is set up. Taking a naval ship as an example, the major parameters related to COGAG power plant performance are obtained by com- puter simulation, and a set of synthetic performance evaluation index system is established. The result shows that the strong fuzzy propulsion system performance indexes can be quantified by this fuzzy evaluation model in order to provide the reference for choosing the optimal design of ship propulsion system. Keywords COGAG Power Plant, Fuzzy Comprehensive Evaluation, Performance Index 1. Introduction COGAG power plant [1] [2] will have a broad application prospect in the future, because its excellent maneuver capability, high single power density and adaptation for large range working condition. The propulsion system consists of four gas turbines (GT), two gearboxes, and two controllable pitch propellers (CPP). Two shaft gen- erators are directly mounted on the shafts. The ship is able to operate in several propulsion modes: one to four gas turbines, one or two shaft lines, etc. [3]. The performance of power plant directly affects the economy and mobility of entire ship so that evaluating its performance could provide referential evidence when applied to de- sign other type of power plant. On basis of fuzzy comprehensive evaluation, this paper establishes multilevel fuzzy evaluation model of COGAG power plant by depending on some major parameters obtained by computer simula t io n. With this model, the performance of COGAG power plant is analyzed to offer data for the users and decision-ma ker s. 2. Principle of Fuzzy Comprehensive Evaluation Method Fuzzy comprehensive evaluation method is a synthetic evaluation method based on fuzzy mathematics [4]. The  M. L. Shao et al. evaluation method changes the qualitative evaluation into quantitative one according to the principle of mem- bership degree in fuzzy mathematics. The fuzzy comprehensive evaluation method is suitable for solving Non- deterministic problems because of its features, such as clearer result, systematic approach and making solutions about fuzzy and difficult-quantized problem. Fuzzy synthetic evaluation model is mainly made up of single- level fuzzy comprehensive evaluation model and multi-level fuzzy comprehensive evaluation model [5]. 2.1. Single-Level Fuzzy Evaluation Model The 3 elements of the comprehensive evaluation: factors set, remark set, single factor evaluation set. Factors set , the set of factors about the object of being judged. Remark set , the set of comments. Single factor evaluation set means the evaluation of single factor in (i = 1, 2, , n), and gets the fuzzy set ( , , …, ) in V, which is a fuzzy mapping from U to V, thus the fuzzy set ( , , …, ) in V can be got. Fuzzy mapping f can determine a fuzzy relationship , called evaluation matrix, which is composed of single factor fuzzy sets for evaluation. 11 121 21 222 12 m m n nnm rr r rr r R rr r ⋅⋅⋅ ⋅⋅⋅ = ⋅⋅⋅⋅⋅⋅ ⋅⋅⋅⋅⋅⋅ ⋅⋅⋅ Because of the differences of each single factor, all factors are needed to be weighted; using fuzzy set in U represents the weight distribution of each factor. As Equation (1) shows, the compre- hensive evaluation for each factor is composed fuzzy set A with evaluation matrix R. (1) 2.2. Multi-Level Fuzzy Evaluation Model In complex system, satisfactory result can’t be obtained easily by using 1st-level fuzzy comprehensive evalua- tion model when the factors of the evaluation object are more than usual, where exists different levels between each factor. Evaluation factors should be classified due to the characteristics of evaluation object, and evaluated synt het ically level by level, which is multi-level fuzzy comprehensive evaluation. The steps of multi-level fuzzy comprehensive evaluation are as follows: • Divide the evaluation factors set U into m subsets according to the attributes, which meets Equation (2): , (2) • Pre According to Equation (2), the second-level evaluation factors set can be got. ( , ) means evaluation factors in the subset , which could be evaluated by using the single-level fuzzy comprehensive evaluation model. If the weight distribution in is , the corresponding evaluation matrix is . The comprehensive evaluation result of the i-th subset can be got as Equation (3): 12 [,,, ] iiii iin BARbbb= = (3) • Evaluate synthetically for the m evaluation factors subsets in U, the decision matrix is R (see Equation (4)). 111 121 221 222 12 n n mm mmn B bbb B bbb R B bbb ⋅⋅⋅ ⋅⋅⋅ = = ⋅⋅⋅ (4 ) 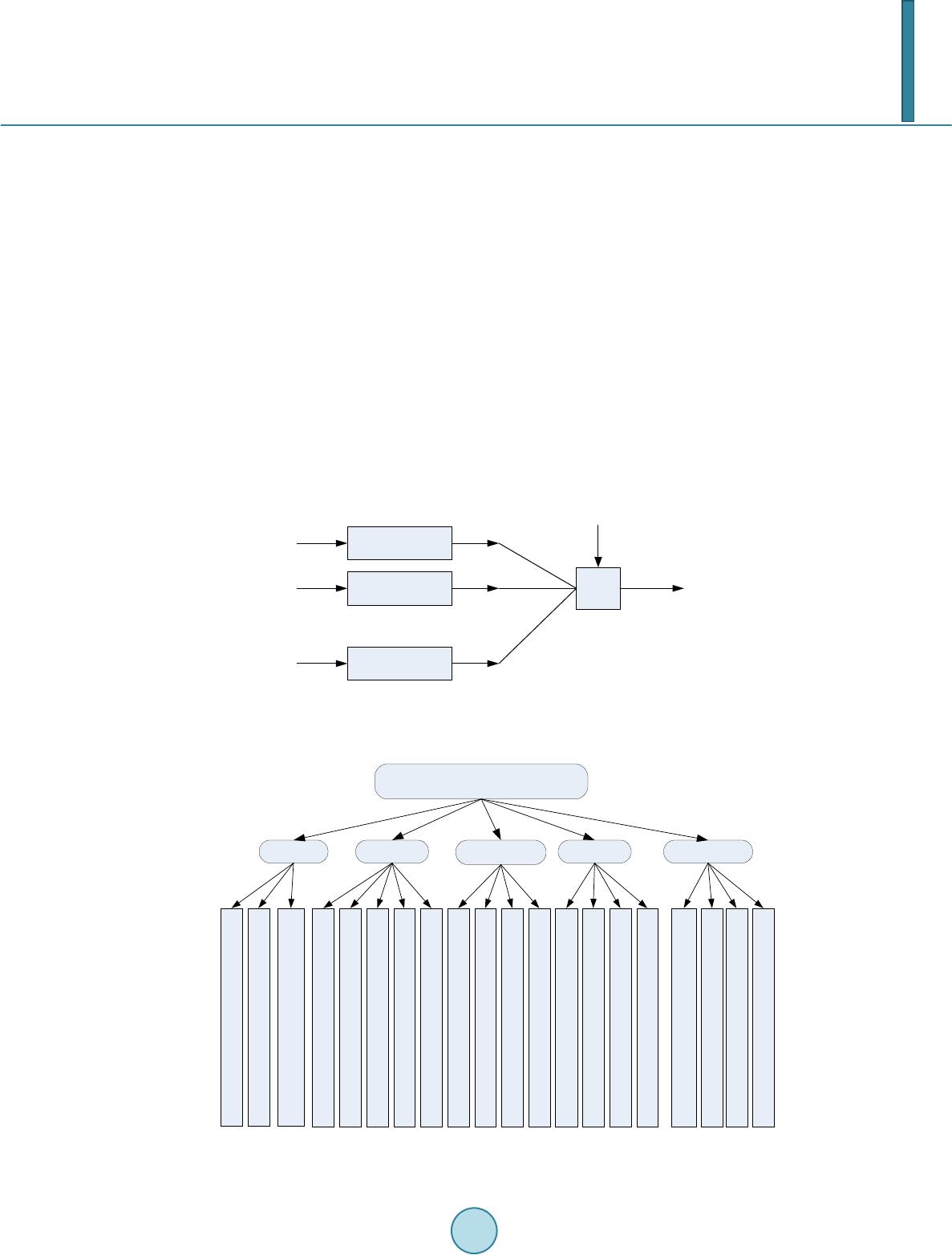 M. L. Shao et al. If weight of each evaluation factors subsets in U is A, the result of evaluation is . Similarly, Con- struct third-level, fourth-level fuzzy synthetic evaluation model could be worked out. Figure 1 shows the sketch map of second-level fuzzy synthetic evaluation model. In conclusion, the (U, V, R) fo rms a fuzzy comprehensive evaluation mathematics model. The fuzzy transform R in which change fuzzy subset in U to fuzzy subset B in V. The B is a fuzzy comprehensive evaluation to the evaluation object. 3. Application Example 3.1. Performance Index Framework Analysis On the base of the principle of maximum membership degree and fuzzy linear transformation, main relevant in- dexes are taken into consideration to make a reasonable assessment, which is the basic idea of fuzzy compre- hensive evaluation. The performance indexes of power plant are determined by the type, primary skill parame- ters and driving methods of engine [6]. For COGAG power plant, the performance evaluation indexes are di- vided into 3 layers by screening. The following are estimate index of each level: • The target layer: Comprehensive performance evaluating system of COGAG power plant. • The firs t-degree index: 1) Economy; 2) Flexibility; 3) Co nce a l ment; 4) Reliability; 5) Repairable. • The second-degree index: As Figure 2 sho ws, there are 22 indexes corresponded with first-degree index. Figure 1. The sketch map of second-level F uzzy comprehensive evalu- ation model. comprehensive performance evaluating indexes of COGAG propulsion system economy flexibility concealment reliabilityrepairable Power plant fuel consumption Cruising endurance Cost of equipment procurement and research Switch time from cruise to both machine Switch time from both machine to full speed Switch time from full speed to both machine Switch time from both machine to cruise Underwater noise Aerodynamic noise Vibration intensity Infrared stealth and Stealth performance Gas turbine reliability Line shafting reliability Propeller reliability gear box reliability Single part maintenance time Maintenance difficulty Spare parts supply Average pre-maintenance time Maximum speed arrival time Figure 2. The sketch map of multilevel performance evaluation index of COGAG power plant. R1 R2 Rm R . . . . . . . . . A1 A2 Am B1 B2 Bm B=A×R A=(a1,a2,…,am) `  M. L. Shao et al. 3.2. Index Weight The major parameters related to COGAG power plant performance are obtained by simulation. Then, the in- volved factors are graded according to experts grading method, thus the weight of each index is achieved [7]. With a view to the difference from invited experts, 3 groups are divided, which have been given corresponding wei g h t. The specific data can be seen from Table 1. Table 2 displays Weight for performance indexes and mean for evaluation of all experts. Table 1. Subgroup of experts and weight distribution. Subgroup Number We ig h t 1 of Ship Design Dep a rt ment 2 0.079/0.077 1 0.078 2 0.075/0.062 2 1 0.063 2 0.067/0.061 -professor 1 0.062 3 -root Units 2 0.064/0.061 rship 3 0.058/0.059/0.060 1 0.074 Table 2. Weight for performance indexes and mean for evaluation of all experts. First-degree index Wei gh t S ec on d-degree index W ei gh t M ea n Econ omy 0.34 Power plant fuel consumption 0.33 0.81 Cruising endurance 0.37 0.93 Cost of equipment procurement 0.14 0.65 Cost of equipment research 0.16 0.73 Flexibility 0.24 Maximum speed arrival time 0.24 0.88 Switch time from cruise to both machine 0.23 0.76 Switch time from both machine to full speed 0.28 0.58 Switch time from full speed to both machine 0.12 0.43 Switch time from both machine to cruise 0.13 0.75 Con c ea lm en t 0.09 Underwater noise 0.31 0.47 Aerodynamic noise 0.26 0.39 Vibration intensity 0.14 0.66 Infrared stealth 0.21 0.75 Stealth performance 0.08 0.55 Reliability 0.23 Gas turbine reliability 0.22 0.49 Line shafting reliability 0.25 0.48 Propeller reliability 0.28 0.77 gear box reliability 0.25 0.81 Repairable 0.10 Maintenance difficulty 0.27 0.90 Spare parts supply 0.32 0.87 Single part maintenance time 0.21 0.56 Average pre-maintenance time 0.20 0.51  M. L. Shao et al. 3.3. Remark Set All possible results of assessment constitute remark set. As for this study, remark set is divided into 4 ranks such as excellence, fine , qualification, disqualification (see Equation (5)). 4 remark grades are transformed into the corresponding evaluation one (see Equation (6)). (5) In the equation: V—remark set; V1—excellence, 90 ≤ F < 100; V2—fine, 75 ≤ F < 90; V3—qualification, 60 ≤ F < 75; V4—disqualification, F < 60. (6) 3.4 Evaluation Mat ri x The elements in Evaluation matrix indicate the degree of membership of Second-degree index, which can be obtained from the result of experts grading method. Equation (7) means the Evaluation matrix of e co nomy. Similarly, can be got. 1 0.6 0.20.1 0.1 0.5 0.30.1 0.1 0.4 0.2 0.2 0.2 0.3 0.2 0.2 0.3 R = (7) 3.5. Fuzzy Comprehensive Evaluation The weight of first-degree estimate index: (0.34,0.24,0.09,0.23,0.10)A= The weight of second -degree estimate index: 2 {0.24,0.23,0.28,0.12,0.13}A= 3 {0.31,0.26,0.14,0.21,0.08}A= The results of second -degree estimate are as follows: 1 11 (0.487,0.237,0.13,0.146)B AR =×= 2 22 (0.496,0.241,0.175,0.088)B AR=×= 3 33 (0.325,0.278,0.165,0.232)B AR =×= 4 44 (0.5,0.266,0.181,0.053)B AR=×= 5 55 (0.553,0.248,0.179,0.02)B AR=×= The final evaluation result of COGAG power plant performance, as show below: 1 2 3 4 5 0.487 0.2370.130.146 0.4960.241 0.175 0.088 0.325 0.278 0.165 0.232 0.50.2660.1810.053 0.553 0.248 0.1790.02 B B RB B B = =  M. L. Shao et al. (0.484,0.249,0.161,0.106)B AR=×= The evaluation results: According to the principle of maximum membership degree, the overall goal of the general reviews is 77.195, and its evaluation level is fine. 4. Conclusions The main conclusions of this work are the following: • Results show that, the integrated index rank of this type was between excellence and fine which can guaran- tee the safety work of the ship. But the probability in the fine grade was higher which showed that the per- formance of this COGAG power plant should be improved and optimized. • Comprehensive estimate of the power plant from the experts showed that the cover-up performance was worse. The box, shock isolation device and the coating absorbing technique could be used to the invisible goal. Shock isolation device was added in this system which could strengthen the damping of the mechanical stress wave so as to shortening the oscillation intensity. • Proper parameter was chosen based on the comprehensive evaluation model on the performance of the COGAG which could quantity the performance index that is blurred. Then, reliable basis of design and de- monstration of the power plant could be obtained. • The principle and theory of the method could be used to estimate the performance index of other type of power plant. The method could be translated and edited in computer program which can be used to the performance analy- sis of other kinds of power plant. References [1] Yu, Y.-H., Sun, F.-R. and Liu , Y.-B. (2008) Analysis of Load Efficiency Characteristics of COGAG Power Plant Based on Dynamic Simulation. Ship Engineering, 30. [2] Gu, H.W. (2012) Research on Parallel Method of COGAG. Harb in Engineering University, Harbin. [3] Altosole, M., Benvenut o, G., Figari, M. and Campora, U. (2009) Real-Time Simulation of a COGAG Naval Ship Pro- pulsion System. Engineering for the Maritime Environment, 223, 47-61 . [4] Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X [5] Yang, L.-B. and Gao , Y.-Y. (2011) Principle and Application of Fuzzy Mathematics. South China University of Tech- nology Press. [6] Manuel, V., Dolores, D.M. and Antonio, R. (2003) Thermoeconomic Optimization of Combined Cycle Gas Turbine Power Plants Using Genetic Algorithms. Applied Thermal Engineering, 23, 2169-21 82 . [7] Lian g, Q.-C. and Zhang, S. (2011) Research on Fuzzy Judge Model of Ship Propulsion System. 2011 IEEE Interna- tional Conference on Intelligent Computing and Integrated Systems, Gui Lin, 1, 451 -453.
|