 Journal of Power and Energy Engineering, 2014, 2, 1-7 Published Online September 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.29001 How to cite this paper: Liu, G.Y., Wu, Y. and Liao, B.T. (2014) Impact of Vibration Models on Heat Capacities of HF Molecu- lar System. Journal of Power and Energy Engineering, 2, 1-7. http://dx.doi.org/10.4236/jpe e. 2014.29001 Impact of Vibration Models on Heat Capacities of HF Molecular System Guo Yue Liu, Ying Wu, Bi Tao Liao Research Center of Computational Physics, Mianyang Normal University, Mianyang, China Email: guoyueliu@sohu.com Received May 2014 Abstract Based on the analysis of completeness and finiteness of HF molecular vibrational levels, HF sys- temic vibrational heat capacity is studied with quantum statistical and full set of vibrational en- ergy level determined AM (algebraic method). The results show that correct vibrational descrip- tion and vibrational energy level set of HF system are key factors in calculating heat capacity, HF heat capacity data determined by AM energy spectra {Eυ} are much superior to the ones of har- monic oscillator model, AM results are agreement with experiment data. Keywords HF Molecule, Vibrational Energy Level, Quantum Ensemble, Molar Heat Capacity 1. Introduction It is well known that macroscopic thermodynamic system is consists of many molecules, vibration is molec ular intrinsic movement. Molecular vibration directly effects for systematic macroscopic thermodynamic properties (TDP), for example, affect the heat capacity of actual gas. Diatomic molecular vibration makes contributions for thermodynamic properties of macroscopic systems, the problems have been the important topics worth studying, there are some meaningful results [1] [2]. How to deal with diatomic molecular v ibration al energy is important and difficult to solve the thermodynamic properties (TDP) using statistical methods. For example, diatomic molecular vibration was seen as a simple harmonic vibration, quantum summation was usual over 0 → ∞ in computing vibrational partition function (VPF) [3]. But diatomic molecular is not simple harmonic oscillator (SHO), there is actually not infinite v ibr a- tional levels, too. Important SHO heat capacity cannot show reasonability in wider temperature range. The po- tential energy function (PEF) with good physical behavior should be necessary. Morse function [4], MS poten- tial (Murrell-Sorbie) [5], ECM potential (energy-and consistent-method) [6] [7], and so on, they are all good analytical potential energy functions. In 1932, Dunham proposed an analytical diatomic molecular vibra- tion-rotation level formula [8]. Since high order vibration coefficients and the number of vibrational levels are difficult to be determined, so far the thermodynamic work report has not been seen. In 1953, Herzberg proposed an important vibration level formula, coefficients or levels can be directly determined by related vibration spec- trum data [9]. Sin ce the selected number of expansion item is uncertainty and the analytical expression is more  G. Y. Liu et al. complexity, the work used Herzberg’s vibrational levels has not been seen, too. Once the number of vibrational levels is un limited, the paradox will be inevitable t hat the vibration energy level can be greater than the diatomic molecular dissociation energy. It is obvious that accuracy and finiteness of vibrational energy spectrum (a full set of vibrational levels) are essential to study on macroscopic thermody- namic properties (TDP). Ab initio should be a meaningful way to directly obtain numerical vibration levels. But there are differences between ab initio levels and experiment data, the differences will rise as vibrational quan- tum number increases [10]. There are some experiment data like RKR data [11]-[13], too. But such data are of- ten difficult to give high vibrational levels and the highest vibration quantum number. In this work, the algebraic method (AM) proposed by Sun Weiguo [14] is adopted to obtain a full set of vibra- tion energy level and maximum quantum number of HF molecular in ground state. Using quantum statistical ensemble theory, the statistical contributions for vibration heat capacity of HF gas are discussed. 2. The Full Set for Vibrational Energy Level of HF in Ground State X1Σ+ The ground state X1Σ+ of hydrogen fluoride is particularly well characterized by spectroscopic methods and very precise molecular constants for the lower vibrtional levels are available. HF is important for high - efficiency chemical lasers in the infrared (IR) and far infrared (FIR), and the ground state pure rotational transitions of HF serve as accurate wavelength standards for IR and FIR spectroscopy [15]. In 1975, W. Meyer and P. Rosmus used coupled electronic pair approach (CEPA) method to study the spectra data and the potential energy behav- ior of HF molecule in ground state and given dissociation energy De = 5.83 eV [16]. In 1990, J. A. Coxon et al. studied the vibration energy levels of HF in ground state, 20 vibrational levels were given, and at the vibrational quantum number υ = 19, relative vibrational level is 49026.508 cm−1 [15], but the number of vibrational energy levels in the ground state of HF did not give. The high order expansion of diatomic molecular vibration level was derived by Sun Weiguo and his collabo- rators us ing second order perturbation theory [14]. 2 00 3 45 67 11 () 22 111 222 11 22 e eee eeeeee e eee Ex yzt sr υ ωωω υωυ ωυω υωυ ωυ ωυ =+ ++−+ +++++ + + ++ ++ (1) where υ is vibrational quantum number, ω 0, ω 0e, ω e, ω exe, ω eye, ω exe, ω exe, ω exe and ω exe are molecular vibra- tional spectroscopy data, ω 0 and ω 0e are two new small quantities which are absence in Herzberg’s level formula [9]. The Algebraic method (AM) determined diatomic molecular vibrational energy level was put forwarded by Sun Weiguo [14]. Using method, Equation (1) can be rewritten as an algebraic equation AX = E (2) where the spectrum data solution matrix X and the level matrix E are 0 e e ee X r ω ω ω ′ = (3) The matrix A is an 8 × 8 coefficient square, its matrix element is Aυk = (υ + 0.5)k. A group of vibrational en- ergy level, whose number is , can be obtained with modern experimental technologies, chosen eight vi- brational levels from m levels are instituted into Equation (2), a set of vibrational spectrum constants X can be solved using the standard algebraic method. There are different selection schemes, which give N ma- trixes of vibration spectrum constant Xe. In the resolved matrixes, there is always a group of vibration spectrum data can best meet with the requirements of the following physical conditions [14]. maxmax 1 ,1 mm E EE υυυ υ − − ∆ =−→ as small as possible (4)  G. Y. Liu et al. 12 ,exp , 0 1 (,)|| 0 m cal v EecE E m υυ − = ∆=− → ∑ (5) (6 ) maxmaxmaxmax max2max max 2,1 ,,1 /( ) cal e DE EEE υυ υυυυυ −− ≅ +∆∆−∆ (7 ) max max exp ,1 0 ()/1 cal rror ee E DD E υυ − <= −∆≤ ( 8) In 2008, a full set { }of vibrational levels,the highest vibrational quantum number υmax and dissociation energy De of HF in X1Σ+ state have been obtained by Liu Yi-Ding, Sun Weiguo et al. with AM method [17]. The AM data and experiment data [15] are all listed in Table 1. The full set { } of vibrational levels and maximum vibration quantum number υmax determined with AM method from the finite and precision experimental vibrational levels are the important basis on the stud y of macroscopic thermodynamic properties of real gas HF. 3. Statistical Methods and Results The core and important basis of quantum statistical theory are distribution function of statistical ensemble. In this study, the set energy level { } of HF is not analytical bu t numerical, the number of real vibration levels is limited but unlimited. When vibration quantum number υ is greater than the υmax, the corresponding vibratio- nal levels does not actually exist. In calculating the partition function, these vibrational levels should be not in- cluded in the sum of vibrational levels. Using the canonical quantum ensemble, the vibrational partition function Table 1. Comparisons of different vibrational energy spectra of HF in X1Σ+ (in cm−1). υ exp [15] AM 0 2050.771 2050.771 1 6012.194 6012.194 2 9801.56 9801.895 3 13423.603 13424.012 4 16882.448 16882.721 5 20181.824 20181.824 6 23324.620 23324.482 7 26313.146 23613.042 8 29148.927 29148.927 9 31832.367 31832.531 10 34362.909 34363.093 11 36738.405 36738.494 12 38954.943 38954.943 13 41006.593 41006.508 14 42884.443 42884.443 15 44576.055 44576.279 16 46064.207 46064.629 17 47325.663 47325.663 18 48328.541 48327.221 19 49026.508 49026.508 20 49367.340 49380.000  G. Y. Liu et al. is [3] (9 ) where gυ (=1) is the degeneracy of vibr ational level of HF in ground state, k is Boltzmann constant and β = 1/kT. Molar heat capacity is [3] 2 ln( ) mA CNkTQT TT υ ∂∂ = ∂∂ (10) In statistical physics, molar heat capacity is an important observable quantity. For HF macro system, as te m- perature is not very high, the thinking may be reasonable that the vibration of HF in electronic ground state makes only real contribution for vibrational heat capacity. A kind of common practice was that simple harmonic oscillator (SHO) model was used, and sum was over infinite vibrational levels, the operation is equivalent with υmax → ∞, and the sum is deservedly changed into integral. So thus obtained partition function is an a l yt ical form [3] /2 () 1 e e cal SHO e QT e βω βω − − =− (11 ) The result leads to analytical vibrational heat capacity. ( ) 2 ,2 ( 1) e v cal SHO Ae e C Nke βω υβω βω =− (12) where NA is Avogadro constant. R (=kNA) is universal gas constant. In fact, it is not reasonable for simple harmonic oscillator (SHO) model to be used to discuss thermodynamic properties of real macro system, υmax is not infinite. As real number of diatomic molecular vibration levels is generally dozens or even hundreds, so that it hard to obtain analytical solution of thermodynamic properties, and the calculations are usually complex. For example, AM method have been used to calculate full vibrational en- ergy spectrum {Eυ} and maximum vibrational quantum number υmax of HF in ground state, obtained υmax = 20. Molar internal energy, entropy, heat capacity and other macroscopic thermodynamic properties of statistical system made of HF in ground state can be obtained. But the results are not equal to one’s of summation over in- finite items. For example, molar vibrational heat capacity should be expressed as [3] ( ) 22 ,2 cal A AM N C EE kT υ υυ =<>−< > (13) where <Eυ > is statistical average of finite vibrational levels and < > is statistical average of square of finite vibrational levels, they are respectively decided by the following formulas [3] max 0 max 0 E E gEe E ge υ υ β υυ υ υβ υ υ − = − = < >= ∑ ∑ (1 4) max 2 20 max 0 E E gEe E ge υ υ β υυ υ υβ υ υ − = − = < >= ∑ ∑ (1 5) Based on the theory of quantum statistical ensemble, using above the accurate full set of { } vibrational energy spectrum and υmax of HF in ground state, its vibrational heat capacity can be obtained. 4. Theoretical Results and Comparison Hydrogen fluoride is colorless gas. It is the principal industrial source of fluorine, component of many super- acids and precursor to many important compounds including pharmaceuticals and polymers. Study on the heat  G. Y. Liu et al. capacity of hydrogen fluoride gas is important. To test the correctness of theoretical results, these results will be compared with reliable experimental data. In this work, reference [18 ] gives experimental heat capacity (in constant pressure) data of HF gas. To convert these data to vibrational molar heat capacity and to reduce complicacies from intermolecular interactions in actual gas, the chosen temperature range (1000 K ~ 3 000 K) should be suitable to ideal gas that there are not obvious errors in relevant data, the translational and rotational heat capacities have been deducted. The three kinds of vibrational heat capacities , and (their unit are J/mol∙K) and c al cu- lated relative percentage error δ AM and δ SHO are all listed in Table 2. In given temperature range, the SHO heat capacity goes prematurely into the expected scope of the classical energy equipartition theorem, AM vibrational heat capacities and experimental heat capacities are much smaller than SHO vibra- tional heat capacities . At 1000 K, the relative error δ SHO is as high as 659.12%, heat capacity is too much larger than theoretical and experimental , but the relative error δ AM is on ly −14.59%. At 2000 K, δ SHO is still as high as 68.38%, the relative error δ AM has been down to −7.56%. The relative errors δ SHO are so large that the can not be used in all cases. On the whole, AM data are qualitative agree- ment with experimental data. Relative errors δ AM may be acceptable for actual works. Figure 1 obviously and visually represents the differences and change trends bring three kinds of vibration heat capacity, “*”, “▲” and “○” are , and , respectively. As shown in Figure 1, the vibrational heat capacities from AM full vibrational levels set {Eυ} are obviously superior to one’s of SHO’s. It is easy to see that the rough potential energy function and the summation over infinite levels led to devia- tion from real situation. The differences from heat capacities determined by limited AM vibrational lev- els with experimental data are obviously superior to one’s of SHO. But relative errors are still bigger. There can be the causes, molecular rotation may be non-rigid , the coupling of molecular vibration—rotation are not con- side red, some molecules are excited. The problems will be discussed in other papers. Table 2. Comparisons of different vibrational heat capacities. T 103K δ AM % δ SHO % 1.0 1.103 8.115 1.069 −14.59 659.12 1.1 1.275 8.149 1.459 −12.61 458.53 1.2 1.672 8.176 1.929 −13.84 323.85 1.3 2.061 8.196 2.369 −13.00 245.97 1.4 2.458 8.212 2.789 −11.87 199.44 1.5 2.846 8.225 3.189 −10.76 157.92 1.6 3.219 8.236 3.559 −9.55 131.41 1.7 3.573 8.245 3.919 −8.83 110.39 1.8 3.906 8.252 4.259 −8.29 93.75 1.9 4.218 8.259 4.579 −7.88 80.37 2.0 4.510 8.264 4.879 −7.56 68.38 2.1 4.781 8.269 5.169 −7.51 59.97 2.2 5.033 8.273 5.449 −7.63 51.83 2.3 5.267 8.276 5.709 −7.74 44.96 2.4 5.485 8.279 5.949 −7.80 39.17 2.5 5.687 8.282 6.179 −7.96 34.03 2.6 5.867 8.285 6.399 −8.31 29.47 2.7 6.050 8.287 6.609 −8.46 25.39 2.8 6.213 8.289 6.799 −8.62 21.92 2.9 6.366 8.290 6.989 −8.91 18.61 3.0 6.508 8.292 7.159 −9.09 15.83 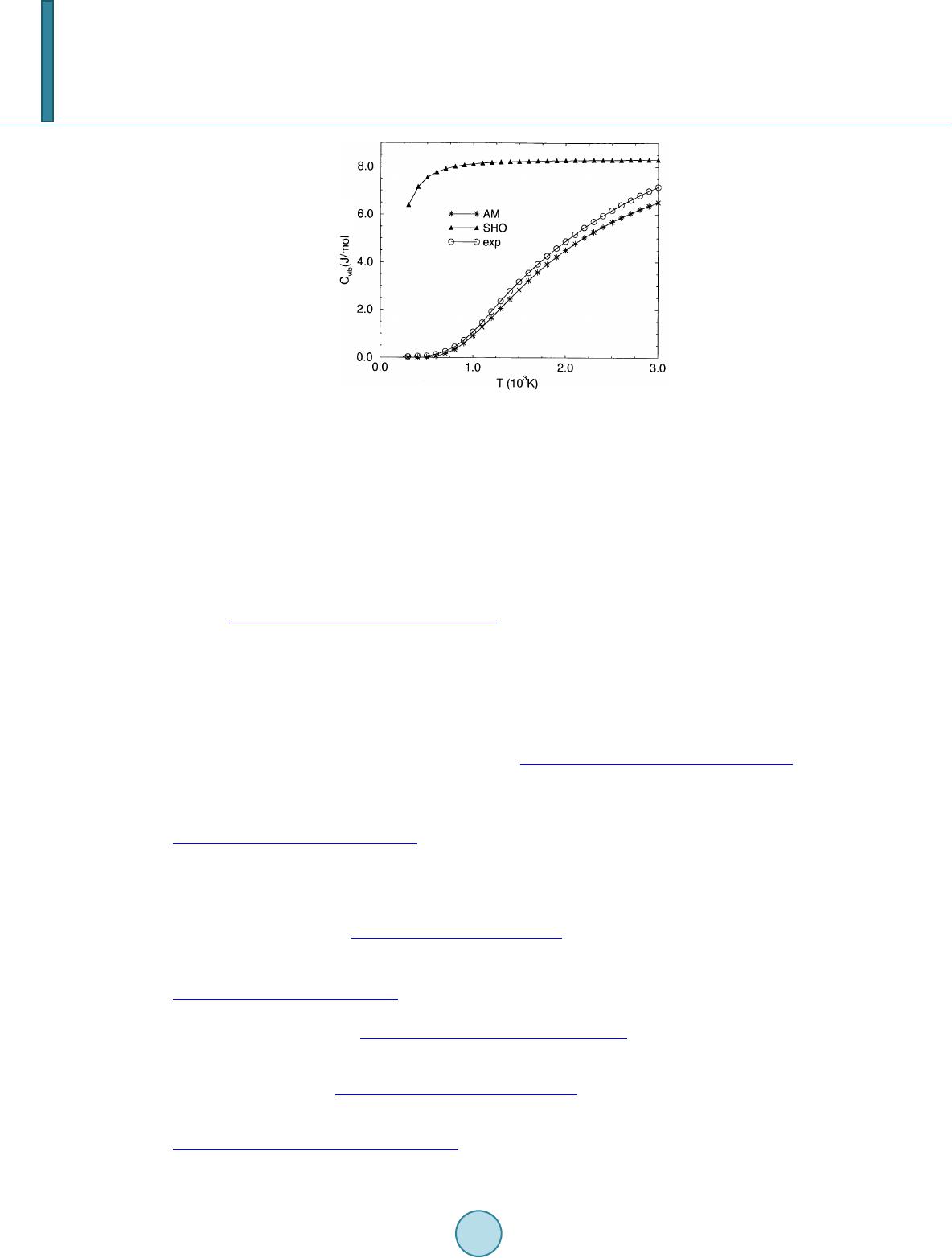 G. Y. Liu et al. Figure 1. Comparison of heat capacities Cυi. Acknowledgements This work is supported by the science Foundation of Department of Science and Technology of Sichuan Pro- vince (2013JY0077). References [1] Ambaye, H. and Manson, J.R. (2006) Calaulations of Accommodation Coefficients for Diatomic Molecular Gases. Physical Review E, 73, 031202. [2] Tandon, P. and Uttam, K.N. (2009) Thermodyamic Properties of Platinum Diatomics. Platinum Metals Review, 53, 123-134. http://dx.doi.org/10.1595/147106709X463688 [3] Pathria, R.K. (1977) Statistical Mechanics. 2nd Edition, Pergamon Press, London, 100-107. [4] Morse, P.M. (1929) Diatomic Molecules According to Wave Mechanics.Ⅱ. Vibrational Levels. Physical Review, 34, 57-60. [5] Murrell, J.N. and Sorbie, K.S. (1974) New Analytic Form for the Potential Energy Curves of Stable Diatomic States. Journal of the Chemical Society, Faraday Transactions 2, 70, 1552-1557. [6] Sun, W.G. (1997) The Energy—Consistent Method for the Potential Energy Curves and the Vibrational Eigenfunction of Stable Diatomic States. Molecular Physics, 92, 105-109. http://dx.doi.org/10.1080/00268979709482078 [7] Sun, W.G. and Feng, H. (1999) An Energy Consistent Method for Potential Energy Curves of Diatomic Molecules. Journal of Physics B, 32, 109-5113. [8] Dunham, J.L. (1932) The Energy Levels of a Rotating Vibrator. Physical Review, 41, 721-731. http://dx.doi.org/10.1103/PhysRev.41.721 [9] Herzberg, G. (1953) Molecular Spectra and Molecular Structure (I), Spectra of Diatomic Molecules. Van Nostrand, New York, 92. [10] Bytautas, L., Matsunaga, N., Scuseria, G.E. and Ruedenberg, K. (2012) Accurate Potential Energy Curve for B2Ab Ini- tio Elucidation of Experimentally Elusive Ground State Rotation—Vibration Spectrum. The Journal of Physical Chemistry A, 116 , 1717-1729. http://dx.doi.org/10.1021/jp210473e [11] Redberg, R. (1931) The Ro-Vibrational Energy Levels of Diatomic Olecules. Zeitschrift für Physik, 73, 376-385. [12] Klein, O. (1932) Zur berechnung von Potential kurven für zweiatominge molecule. Zeitschrift für Physik, 76, 226-334. http://dx.doi.org/10.1007/BF01341814 [13] Rees, A.L.G. (1947) The Calculation of Potential-Energy Curves from Band-Spectroscopoc Data. Proceedings of the Physical Society, 59, 998-1010. http://dx.doi.org/10.1088/0959-5309/59/6/310 [14] Sun, W.G., Hou, S., Feng, H. and Ren, W.Y. (2002) Studies on the Vibrotional and Ro-Vibratioal Energies and Vibra- tional Force Constants of Diatomic Molecular States Using Algebraic and Variational Methods. Journal of Molecular Spectroscopy, 215, 93-105. http://dx.doi.org/10.1006/jmsp.2002.8619 [15] Coxon, J.A. and Hajigeorgiou, P.G. (1990) Isotopic Dpendence of Born Oppenheimer Breakdown Effects in Diatomic Hydrides: B1Σ+ and X1Σ+ States of HF and DF. Journal of Molecular Spectroscopy, 142, 254-278. http://dx.doi.org/10.1016/0022-2852(90)90182-P  G. Y. Liu et al. [16] Meyer, W. and Rosmus, P. (1975) PNO-CI and CEPA Studies of Electron Correlation Effect.Ⅲ. Spectroscopic Con- stants and Dipole Moment Functions for the Ground States of the First-Row and Second-Row Diatomic Hydride s. The Journal of Chemical Physics, 63, 2356-2375. [17] Liu, Y.D., Sun, W.G. and Zhang , J.P. (2008) Studies on the Full Vibrational Energy Spectra and Potential Energy Curves for Ground State of Fluorine Hydrogen HF and Its Cation HF+. Journal of Sichuan University (Natural science Edition), 45, 864-868 (Chinese) [18] Chase Jr., M.W. (1998) NIST-JANAF Themochemical Tables. 4th Edition, J. Phys. Chem. Ref. Data, Monograph 9, 1-1951.
|