 Journal of Computer and Communications, 2014, 2, 31-37 Published Online September 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.211004 How to cite this paper: Novák, D., Slowik, O. and Cao, M. (2014) Reliability -Based Optimization: Small Sample Optimization Strategy. Journal of Computer and Communications, 2, 31-37. http://dx.doi.org/10.4236/jcc.2014.211004 Reliability-Based Optimization: Small Sample Optimization Strategy Drahomír Novák1, Ondřej Slowik1, Maosen Cao2 1Institute of Structural Mechanics, Faculty of Civil Engineering Brno University of Technology, Brno, Czech Republic 2Department of Engineering Mechanics, Hohai University, Nanjing, China Email: novak.d@fce.vutbr.cz Received Ju ly 2014 Abstract The aim of the paper is to present a newly developed approach for reliability-based design opti- mization. It is based on double loop framework where the outer loop of algorithm covers the op- timiz ati on part of process of reliability-based optimization and reliability constrains are calcu- lated in inner loop. Innovation of suggested approach is in application of newly developed optimi- zation strategy based on multilevel simulation using an advanced Latin Hypercube Sampling tech- nique. This method is called Aimed multilevel sampling and it is designated for optimization of problems where only limited number of simulations is possible to perform due to enormous com- putational demands. Keywords Optimization, Reliability Assessment, Aimed Multilevel Sampling, Monte Carlo, Latin Hypercube Sampling, Probability of Failure, Reliability-Based Design Optimization, Small Sample Analysis 1. Introduction Reliability-based optimization is a demanding discipline in which it is necessary to combine the optimization approaches and reliability assessment of structures [1]. Methods for reliability calculation utilize similar simula- tion techniques and stochastic methods such as optimization approaches—it is also usually a repeated solving of problem. Some particular parts of the reliability calculations can be even formulated as an optimization problem (e.g. calculation of reliability index according Hasofer and Lind [2] or imposing statistical correlation between random variables). Therefore a connection of model optimization with its reliability assessment in the form of optimization constraint is a challenging issue. Thanks to the development of computer technology and stochastic, simulation and approximation methods themselves is such connection of optimization process with reliability assessment possible nowadays [3]. This paper presents a newly developed approach to reliability-based design optimization. It is based on double loop framework where outer loop of algorithm covers optimization part of process of reliability-based optimiza- tion and reliability constrains are calculated in inner loop [4]. FORM-based double-loop approach has been  D. Novák et al. proposed by Dubourg in [5] [6]. Innovation of suggested approach is in application of newly developed optimi- zation strategy based on multilevel sampling using an advanced simulation technique. This method was called Aimed multilevel sampling (hereinafter AMS) [3] and it is designated for crude optimization using small num- ber of generated samples. 2. Reliability-Based Optimization Problem 2.1. General Formulation The basic prerequisite for reliability-based optimization is to model a load and structural response using random variables. Depending on the required robustness and accuracy of the mathematical model it is therefore neces- sary to randomize some of its input parameters. If any of the functional parameters are considered to be random, then analysed function itself is consequently also a random function. The general stochastic formulation of the reliabilit y-based optimization problem can be expressed like this: ( ) ( ) ,, ,,f min→ , xY rxYy (1) within constraints: ( ) ( ) ,,,,0 1 j hj top= = , xY rxYy (2) () ( ) ,,,,0 1 i gi tom≤= , xY rxYy (3) whe re x is a vector of deterministic design variables is a vector of random variables, r is a vector of considered probability functions and are statistical parameters of random variables. Numbers p and m indicate a num- bers of constraints functions. In the context of the simultaneous application of reliability assessment and stochastic optimization within one procedure, it has to be noted, that the vector may include two sets of statistical parameters of random vari- ables. The first set of statistical parameters represents the randomization of variables that reflects the natural be- haviour of statistical quantities evaluated on the basis of the experiment. This set of statistical parameters is then used for reliability calculations. The second set of statistical parameters of random variables is then used for op- timization purposes. For optimization those parameters are randomized, for which optimal input combination is searched. Statistical parameters are then selected with regard to the choice of optimization method so that the design space should be covered as evenly as possible. Generally structural design is dependent on variables quantifying the response of the investigated structures to the load (e.g. strains and stresses). Therefore we can define the response of the structure as: (4) whe re x is the vector of deterministic design variables and is a vector of random parameters of the in- vestigated structure (e.g. load or strength). Design requirements can be formulated as: ( ) ( ) ,1 il iiu yYy itom ω ≤ ≤=Ax (5) with given boundaries yil and yiu. Constraints for deterministic design variables can be determined as: (6) Reliability constraints can be expressed by a probability function: ( )( ) ( ) ( ) ,1 iil iiu PP yYyitom ω =≤ ≤=x Ax (7) Let us introduce now the function of overall cost of structure c = c(z), which will serve as the main criterion of optimality. Optimal design vector of input values z* composed of a vector of deterministic design variables x and vector of random variables is determined using a stochastic optimization (e.g. [7]). Then the opti- mization problem can be understood as maximization of reliability, with consideration of constraints, defined as the maximum acceptable cost of structure.  D. Novák et al. ( )() ( ) ( ) , ,1 il iiu PP yYyitommax ω = ≤≤=→x Ax (8) Constrained by: (9) (10) where the design space for the calculation of the probability is defined as: (11) with a given probability distribution, where Ω is the sample space for the probability calculations and Σ is a complete design space of variables. Computational demands of reliability-based optimization are obvious from the formulation above. For the purposes of stochastic optimization it is necessary to repeatedly generate random realizations within the design space Σ. It is also necessary for each of these realizations to calculate the probability of failure in the general case by computationally demanding (mostly numerical) integration of the equation: 121 2 (, ,,),,, f f nn D pf XXXdXdXdX= ∫ (12) whe re Df represents the failure area (that is the area where value of function indicating a failure is <0) and is the joint probability density function of random variables . The quantification of reliability is associated with the repeated evaluation of structural response. It can bring (especially in case of finite element models) enormous demands on the computing time. Therefore lot of ap- proximation methods, which aim to reduce the computational complexity of reliability assessment (FORM, SORM, Response surface methods) [8]-[10], as well as advanced optimization techniques for the small sample analysis [3], [11] have been developed. 2.2. Practical Solution A practical solution to the above-defined optimization problem is performed using the so-called double-loop ap- proach. The algorithm is composed of two basic loops: • The outer loop represents the optimization part of the process based on small-sample simulation Latin hy- percube sampling. The simulation within the design space is performed in this cycle. For obtained design vectors of n-dimensional space xi = (x1, x2,…, xn) objective function values are calculated. The best realiza- tion is then selected based on these values and utilized optimization method. Consequently the best realiza- tion of random vector xi,best is compared with optimization constraints. These constraints may be formulated by any deterministic function which functional value can be compared with a defined interval of allowed values. Constraints are also possible to formulate as allowed interval of reliability index β for any limit state function (within design space of given problem). Calculations of reliability index of each generated random vectors xi takes place in the inner loop. Note that it is recommended to use some of advanced meta-heuristic optimization techniques in this loop such as simulated annealing or Genetics algorithms etc. to avoid local minima. • The inner loop is used to calculate reliability index (FORM-based) either for the need of checking of gener- ated solutions—if they satisfy constraints, or to calculate the actual value of the objective function, if the target reliability index is set as goal of optimization process. 3. Latin Hypercube Sampling For time-intensive calculations, small-sample simulation techniques based on stratified sampling of the Monte Carlo type represent a rational compromise between feasibility and accuracy. Therefore, Latin Hypercube Sam- pling (LHS) [12]-[14], which is well known today, has been selected as a key fundamental technique. LHS be- longs to the category of advanced stratified sampling techniques which result in the very good estimate of statis- tical moments of response using small-sample simulation. More accurately, LHS is considered to be a variance reduction technique, as it yields lower variance in statistical moment estimates compared to crude Monte Carlo sampling at the same sample size; see e.g. [15]. This is the reason the technique became very attractive for deal- 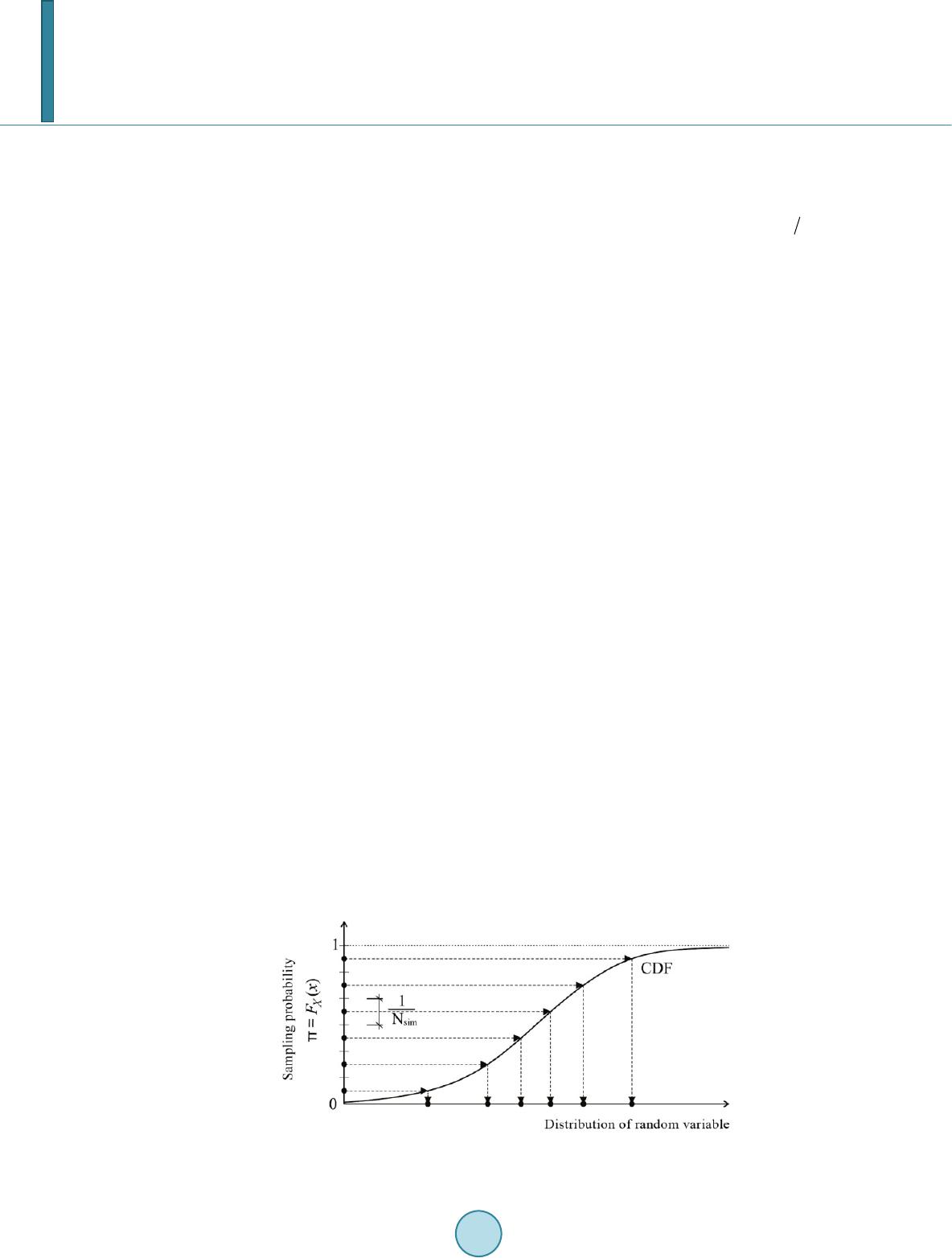 D. Novák et al. ing with computationally intensive problems like e.g. complex finite element simulations. The basic feature of LHS is that the range of univariate random variables is divided into Nsim intervals (Nsim is a number of simulations); the values from the intervals are then used in the simulation process (random selection, median or the mean value). The selection of the intervals is performed in such a way that the range of the proba- bility distribution function of each random variable is divided into intervals of equal probability, . The samples are chosen directly from the distribution function based on an inverse transformation of the univariate distribution function (Figure 1). The representative parameters of variables are selected randomly, being based on random permutations of in- tegers k = 1, 2, ..., Nsim. Every interval of each variable must be used only once during the simulation. Section 5 of this paper is focused at utilization of LHS simulation for purpose of optimization. Uniform cov- erage of design space is required during optimization therefore rectangular distributions are assigned to random variables. In such case LHS median could be recommended for simulation at each level of optimization algo- rithm. 4. Software Tools (FReET) FReET multipurpose probabilistic software for the statistical, sensitivity and reliability analysis of engineering problems (authors: Novák, Vořechovský and Rusina) is based on the efficient reliability techniques described in [16]-[18]. Software allows definition of stochastic model of given problem; perform advanced simulation within design space and calculate reliability using one of built-in methods. FReET enables to define probability distribution function for each random variable (by selection of prede- fined functions and its parameters, based on raw data etc.). For simulation FReET offers simple Monte Carlo method or above described LHS methods (in random, median or mean form). Correlation matrix for random va- riables can also be prescribed. To achieve required correlation structure between generated simulations permuta- tions of generated values, a random vector is optimized using Simulated annealing approach [19]. For reliability calculations FReET enables to use simple Cornell index calculations, Curve fitting technique or First order re- liability method (FORM). Other useful features of FReET are described fully in details in [16]. Software FReET was utilized in a suggested reliability-based optimization approach in both of its loops. Sim- ple software described in [3] was developed to control work of FReET within outer and inner loop of above de- scribed double - loop approach. FORM approximation was applied for reliability calculations in inner loop. State-of-the-art probabilistic algorithms are implemented in FReET to compute the probabilistic response and reliability. FReET is a modular computer system for performing probabilistic analysis developed mainly for computationally intensive deterministic modeling such as FEM packages, and any user-defined subroutines. The main features of the software are (version 1.5): Response/Limit state function • Closed form (direct) using implemented Equation Editor (simple problems) • Numerical (indirect) using user-defined DLL function prepared practically in any programming language • General interface to third-parties software using user-defined *.BAT or *.EXE programs based on input and output text communication files • Multiple response functions assessed in same simulation run Figure 1. Diagram of LHS median simulation. 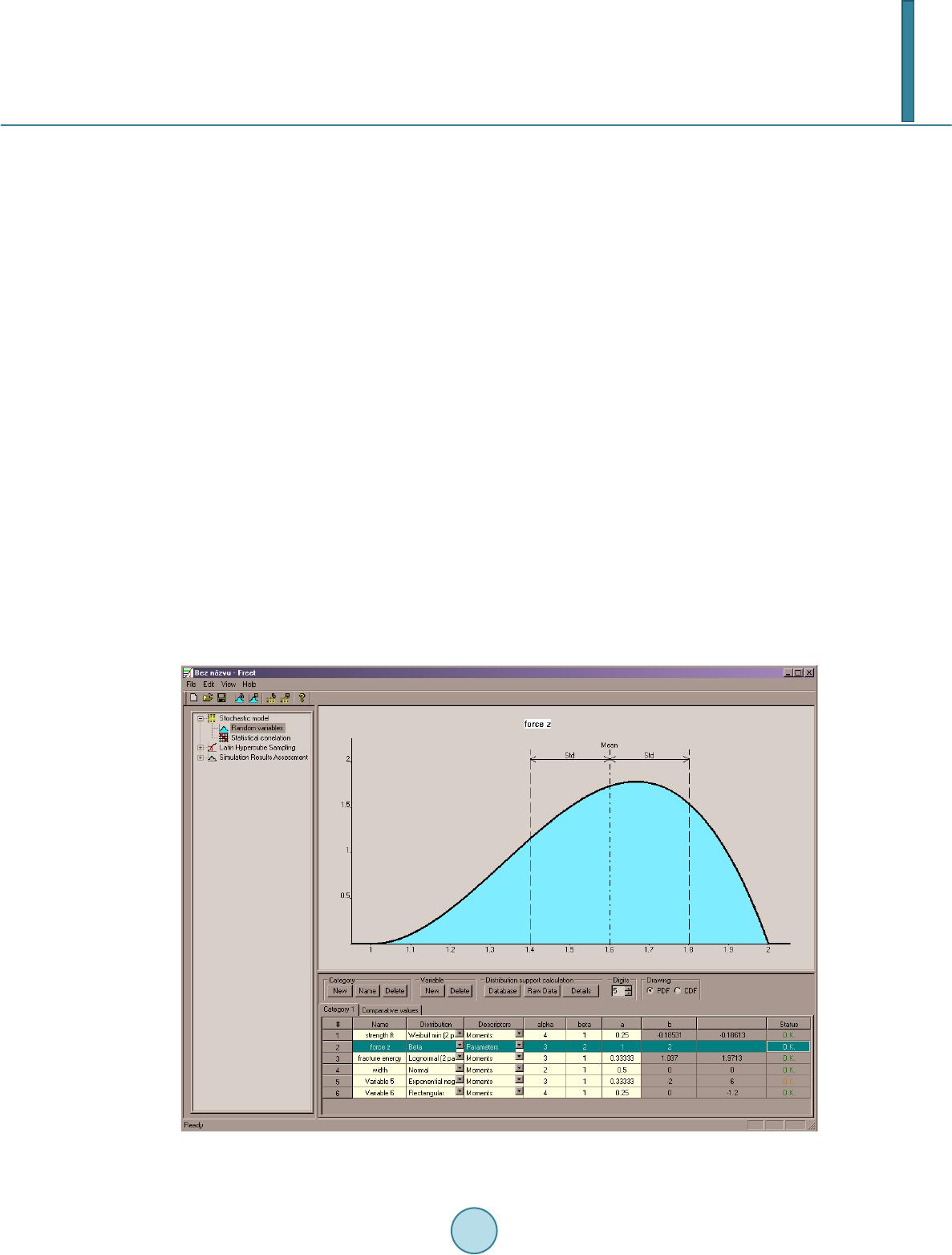 D. Novák et al. Probabilistic techniques • Crude Monte Carlo simulation • Latin Hypercube Sampling (3 alternatives) • First Order Reliability Method (FORM) • Curve fitting • Simulated Annealing • Bayesian updating Stochastic model (inputs) • Friendly Graphical User Environment (GUE) • 30 probability distribution functions (PDF), mostly 2-parametric, some 3-parametric, two 4-parametric (Beta PDF and normal PDF with Weibullian left tail), Figure 2. • Unified description of random variables optionally by statistical moments or parameters or a combination • PDF calculator • Statistical correlation (also weighting option) • Categories and comparative values for PDFs • Basic random variables visualization, including statistical correlation in both Cartesian and parallel coordi- nates 5. Aimed Multilevel Sampling The simplest heuristic optimization method is to perform Monte Carlo type simulation within a design space and select the best realization of random vector (with regard to optimization criteria). Such a procedure clearly does not converge toward function optimum and the quality of solution depends on the number of the simulations. The exact location of the optimum using only simple simulation is highly improbable. Scatter of the results of such optimization is in the case of small sample analysis very high and strongly dependent on the number of simula t i o ns. This approach, however, is very simple requiring no knowledge of features of the objective func- tion and from the engineering point of view is transparent and relatively easy to apply. Figure 2. Window “random variables”.  D. Novák et al. Method Aimed Multilevel Sampling was first suggested in [3]. Its basic idea is to sort the course of the simu- lation into several levels. An advanced sampling (one of the best option is usage of LHS small-sample simula- tion) within a defined multidimensional space will be performed at each level. Subsequently, the sample with the best properties with respect to the definition of the optimization problem will be selected. Design vector Xi,best (x1, x2, ..., xn) corresponding to the best in the i-th level generated sample is determined as a vector of mean valuesof random variables for simulation within the next level of algorithm AMS. Subsequently, the sampling space is scaled down around the best sample. Another LHS simulation is then performed in this reduced space. This leads to more detailed search in the area around the samples with the best properties with respect to the ex- treme of the function. Gradual reduction in the size of the design space can be represented by convergent geo- metrical series. Coefficient q of such series should be selected with respect to number of levels of AMS method to provide an optimal convergence during whole optimization procedure [3]. AMS method is designated for small sample analysis therefore it converge very fast from beginning and convergence slows down with growing number of levels. Also ability to avoid local minima is higher at beginning and decreases at higher levels of AMS algorithm. AMS provides better results within small sample analysis (with usage of only hundreds of simulation) for so far tested optimization problems than other common optimization techniques (e.g. Simulated annealing, Differ- ential evolution method etc.). However more tests of described algorithm should be performed to prove its effi- ciency. The general algorithm of AMS method along with a detailed description of the settings of input parame- ters and comparison of suggested method with other common optimization techniques is presented in [3]. 6. Conclusion The paper presents a summary of newly developed strategy for reliability-based optimization. Suggested ap- proach uses a newly proposed optimization algorithm AMS, which was developed for small sample analysis and existing program FReET for simulation and reliability calculations. Tests of AMS algorithm performed so far provide promising results. However, it is necessary to make another series of tests, especially for high-dimen - sional problems to determine more accurately effectiveness of the proposed method. Detailed information about utilized software and algorithm AMS are available in [3]. Acknowledgements The paper was worked out using the support of projects of Ministry of Education of Czech Republic KONTAKT No. LH12062 and previous achievements worked out under the project of Technological Agency of Czech Re- public No. TA01011019. The project of the specific university research at Brno University of Technology, reg- istered under the number FAST-J-14-2425 should be also acknowledged. References [1] Rackwitz, R. (2000) Optimization—The Basis of Code-Making and Reliability Verification. Structural Safety, 22, 27-60. http://dx.doi.org/10.1016/S0167-4730(99)00037-5 [2] Haso fer, A.M. and Lind, N.C. (1974) Exact and Invariant Second-Moment Code Format. Journal of the Engineering Mechanics Division, 10 0, 111-121. [3] Slowik, O. (2014) Reliability-Based Structural Optimization. Master’s The si s, Brno University of Technology, Brno. [4] Tsompanakis, Y., Lagaros, N. and Papadrakis, M. (Eds.) (2008) Structural Design Optimization Considering Uncer- tainties. Taylor & Francis. [5] Dubourg, V., Noirfalise C. and Bourinet, J.M. (2008) Reliability-Based Design Optimization: An Application to the Buckling of Imperfect Shells. In: 4th ASRANet colloquium, Athens, Greece. [6] Dubourg, V., Bourinet, J.M. and Sudret, B. (2010 ) A Hierarchical Surrogate-based Strategy for Reliability-Based De- sign Optimization. In: Straub, D., Esteva, L. and Faber, M., Eds., Pro ceedings 15th IFIP WG7.5 Conference on Relia- bility and Optimization of Structural Systems, Taylor & Francis, Munich, Germany, 53-60. [7] Marti, K. (1992) Stochastic Optimization of Structural Design. ZAMM—Z. angew. Math. Mech., 452-464. [8] Grigoriu, M. (1982/1983) Methods for Approximate Reliability Analysis. J. Structural Safety, No. 1, 155-165. [9] Bucher, C.G. and Bourgund, U. (1987) Efficient Use of Response Surface Methods. Inst. Eng. Mech., Innsbruck Uni- versity, Report No. 9-87.  D. Novák et al. [10] Li, K. S. and L umb , P. (1985) Reliability Analysis by Numerical Integration and Curve Fitting. Structural Safety, 3, 29- 36. http://dx.doi.org/10.1016/0167-4730(85 )90 005 -0 [11] Ali, M., Pant, M., Abraham, A. and Snašel, V. (2011) Differential Evolution Using Mixed Strategies in Competitive Environment. International Journal of Innovative Computing: Information and Control, 7, 5063-50 84 . [12] Conover, W.J. (2002 ) On a Better Method for Selecting Input Variables. Unpublished Los Alamos National Laborato- ries manuscript, reproduced as Appendix A of Latin Hypercube Sampling and the Propagation of Uncertainty in Ana- lyses of Complex Systems by J.C. Helton and F.J. Davis, Sandia National Laboratories report SAND2001-0417, 1975, Printed No vember. [13] McKay, M.D. and Conover, W.J. and Beckman, R.J. (1979) A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code. Techno metri cs, 21, 239 -24 5. [14] Novák, D., Tep l ý, B. and Keršn er, Z. (1998) The Role of Latin Hypercube Sampling Method in Reliability Engineering. In: Proc. of ICOSSAR—97, Kyoto, Japan, 403 -409. [15] Koehler, J.R. and Owen , A. B. (1996) Computer Experiments . In: Ghosh, S. and Rao, C.R., Eds . , Handbook of Statis- tics, Vol. 13, Elsevier Science, New York, 261-308. [16] Novák, D., Vořechovský, M. and Rusina, R. (20 13) FREET Version 1.6—Program Documentation, User’s and Theory Guides. Brno/Červenka Consulting, Prague. http://www.freet.cz [17] Novák, D., Vořechovský, M. and Rusina, R. (2003) Small -Sample Probabilistic Assessment—Software FREET. In: Proceedings of 9th Int. Conf. on Applications of Statistics and Probability in Civil Engineering—ICASP 9, Rotterdam Mill Press, San Francisco, USA, 91-96. [18] Novák, D., Vořechovský, M. and Rusina, R. (20 09) Statistical, Sensitivity and Reliability Analysis Using Software FReET. In: Furuta, Frangopol and Shinozuka, M., Ed s., Sa fety, Reliability and Risk of Structures, Infrastructures and Engineering Systems, Proc. of ICOSSAR 2009, 10th International Conference on Structural Safety and Reliability, Osaka, Japan. Taylor & Francis Group, London, 2400-2403. [19] Vořechovský, M. and Novák, D. (2009) Correlation Control in Small Sample Monte Carlo Type Simulations I: A Si- mulated Annealing Approach. Probabilistic Engineering Mechanics, 24, 452 -462. http://dx.doi.org/10.1016/j.probengmech.2009.01.004
|