 Journal of Computer and Communications, 2014, 2, 24-30 Published Online September 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.211003 How to cite this paper: Velarde-Alvarado, P., Martinez-Pelaez, R., Ruiz-Ibarra, J. and Morales-Rocha, V. (2014) Information Theory and Data-Mining Techniques for Network Traffic Profiling for Intrusion Detection. Journal of Computer and Com- munications, 2, 24-30. http://dx.doi.org/10.4236/jcc.2014.211003 Information Theory and Data-Mining Techniques for Network Traffic Profiling for Intrusion Detection Pablo Velarde-Alvarado1, Rafael Martinez-Pelaez1, Joel Ruiz-Ibarra1, Victor Morales-Rocha2 1Autonomous University of Nayarit, Area of Basic Sciences and Engineering, Ciudad de la Cultura “Amado Nervo ”, Tepic, Nayarit, Mexico 2Department of Electrical and Computer Engineering, Autonomous University of Ciudad Juarez, Ciudad Juarez, Mexico Email: pvelarde@uan.edu.mx, rafael_uvm @ho tmail .co m, joelruizibarra@gmail.com, victor.morales@uacj.mx Received June 2014 Abstract In this paper, information theory and data mining techniques to extract knowledge of network traffic behavior for packet-level and flow-level are proposed, which can be applied for traffic pro- filing in intrusion detection systems. The empirical analysis of our profiles through the rate of re- maining features at the packet-level, as well as the three-dimensional spaces of entropy at the flow-level, provide a fast detection of intrusions caused by port scanning and worm attacks. Keywords Intrusion Detection, Traffic Profiling, Entropy, and Network Worms 1. Introduction Network Intrusion Detection Systems [1], or NIDSs, have become an important component to detecting attacks against information systems. However, they offer only a limited defense. For instance, a signature-based NIDS (S-NIDS) monitors packets on the network and compares them against a database of signatures or attributes from known malicious threats. A weakness of this type of NIDS is that there will always be a lag between a new threat being discovered and the signature for detecting that threat being applied to the NIDS. During that lag time the NIDS would be unable to detect the new threat. A second type of NIDS is the anomaly-based NIDS (A-NIDS), which monitors network traffic and compares it against an established baseline, [2]. The baseline helps to identify what is normal behavior for that network. If a deviation from the established baseline reaches a specified threshold, an alarm is generated. Therefore, ano- maly detection techniques have the potential to detect new and unforeseen types of attacks. Traditional anomaly based IDSs, employ algorithms that focus primarily on changes in the traffic volume at specific points on the network, and promptly alert the operator of a sudden increase. However, such systems can be evaded through sophisticated attacks that focus on compromising significant hosts, causing them a collapse of memory or CPU  P. Velarde-Alvarado et al. and maintaining a level of traffic within the normal threshold. Recently, a new generation of anomaly based IDSs have emerged, which focus on gaining knowledge in the structure and composition of the traffic and not just its volume. Such systems are based on the fact that the mali- cious activities affect the natural randomness of the network, e.g., they change significantly the entropy of the network [4] [5]. The composition of traffic is related to its probability distribution, and can be characterized by its entropy; a malicious activity changes that composition and the shape of the distribution and therefore its en- tropy. By means of entropy measures to a set of traffic features, we can establish the profiles of normal activity of the network and determine intrusions to the system. This paper presents an analysis at the packet and the flow level on traces obtained through measurements conducted in a campus network under real attacks of the Blaster [6] and Sasser [7] worms, as well as a port scan attack to the proxy server of that network. The captured traces during a week of normal operation, helped to de- velop a profile of normal behavior that is useful to be compared to attack conditions. The paper is organized as follows. In Section 2, we present our profiling approach and the context of this pa- per. Section 3 describes the test environment; Sections 4 and 5 explain the methodology: the rate of remnant items and spaces of entropy and results. Section 6 gives concluding remarks. 2. Profiling Approach We propose two methods for the creation of profiles based on entropy. The analysis applies primarily to the packet-level for the method of the rate of remnant elements and to the flow-level for the spaces of entropy. In- itially, there is a set of captured traffic traces corresponding to five days in typical working hours in an academic LAN. The traces have been inspected to be considered free of anomalies, so they may serve as a baseline. We use traffic features to build the profiles. A traffic feature is a field in a header of a packet (at the packet level) or a field in a five-tuple (at the flow level), respectively. Four fields will be used: source address (srcI P), destination address (d stIP), source port (srcPrt), and destination port (dstPrt). After the feature extraction, an essential part in the builder profile block is the measurement of entropy. For a discrete set of symbols { } with probabilities , , the entropy of the discrete distribution of a random variable associated, is a measure of randomness in the set of symbols and represented as ()( ) 22 1log, 0log MAX n ii i HXppHX Hn = = ≤≤= ∑ (1) The relative uncertainty (RU) provides a measure of variety or uniformity that is independent of the sample size. For a random variable XRU is defined as, [3], ( )( ) ,0 1 MAX HX RURU X H = ≤≤ (2) means that observed values of X are closer to being uniformly distributed, thus less distinguishable from each other, whereas indicates that the distribution is highly concentrated. 3. Experimental Platform The worm propagation and port scanning were carried out on academic LAN which is subdivided into four sub- nets (192.168.1.0, 192.168.2.0, 192.168.4.0, and 10.253.253.0). There are 100 hosts running Windows XP SP2 mainly. One router (192.168.1.1) connects the subnets with 10 Ethernet switches and 18 IEEE 802.11b/g wire- less access points. The data rate of the core network is 100Mbps. A sector of the network is left vulnerable for worm propagation, with ten no Windows XP service pack installed at all (192.168.1.104 - 113). In the experi- ments Blaster and Sasser worms where released in the vulnerable sector. The scanning port attack was observed on the proxy server (192.168.4.253). Data-Set and Tools The benign traffic traces in typical work hours for a period of five days were labeled with a number from one to five. The anomalous traffic for port scanning attack was labeled as 6-P1. Blaster and Sasser worm attacks were labeled as 6-P2 and 6-P4, respectively. The data-set was collected by a network sniffer tool based on libpcap  P. Velarde-Alvarado et al. library used by tcpdump, [8]. All traces were cleaned to remove spurious data using plab, a platform for packet capture and analysis, [9]. Traces were split into segments using tracesplit which is a tool that belongs to Libtrace, [10]. The traffic-files in ASCII format suitable for MATLAB processing were created with ipsumdump, [11]. The flow generation was done with flow analyzer, a tool based on perl and developed by us. 4. Rate of Remnant Elements We define a traffic trace χ of a duration tD seconds with a total of N packets, χ is divided into M non-overlapping slots of seconds each one. The i-th slot has Wi packets for . In each i-slot, four fea- tures are extracted that we associate with a value of r, namely r = 1 for source IP address, r = 2 for destination IP address, r = 3 for source TCP port, and r = 4 for destination TCP port. Let S be a finite sequence of r = 1 values or IP source addresses in a slot-i. This sequence with elements in an alphabet set A, is a function from to A for some . The generated sequence S is denoted by ( ), and the length of S is Wi. The elements of S belong to an alphabet A with cardinality . From A an ordered set ( )( )()( ) { } 12 , ,, o ooo n A aaa= is created, contains the n-source IP addresses in decreasing order sorted by frequency. With the associated frequencies of A, we define a probability mass function (pmf) () ( ) 1 () 1 Pr ,0 rest j ro i jj X f jn j pa = = ≤≤ = (3) where . Ordered set is transferred to an iterative process P to create l subsets of denoted as , . This family of l subsets is shown in Equat i ons (4)-(6) and holds ()()( ) { } , ,1okoko k AAa + = ( ) ()( )( )( )( ) { } ,1 123 ,,,, o oooo on A Aaaaa= = (4) ()( )( )( )( ) { } ,1 234 ,,,, o oooo n A aaaa= (5) ()()( )( )() { } , 12 ,,, ..., olo ooo n lll A aaa a ++ = (6) When in a k-iteration, the relative uncertainty of a partial pmf reaches a threshold β, i.e ., , we say that the iterative process P reached its latest iteration, and hence, k = l. An estimator of relative uncer- tainty for a discrete random variable in the k-iteration is defined in terms of its partial pmf as: ( )( ) ( ) ( ) ( ) ( ) ( ) ( )( ) 22 22 log log ˆ ,ˆlog log oo MAX jj jjj nn rj ijk jk r i papaf f HPX RU Xknk nk H = = = == −− ∑∑ (7) Selecting a , the resultant subset is closer to being uniformly distributed. Then, for a given β, and a number l of iterations carried out, it is possible to calculate the remnant for a subset . Genera- lizing this for an i-slot and a r-traffic feature we have the rate of remnant elements: ( ) ( ) 1 when all,1 for 1 o jj r i n pn n Rnl l a = ≥ =−≥ (8) In other words, is the cardinality of the subset . We found that this feature under normal condi- tions presents regularities that allow creating behavioral traffic profiles. Ta bl e 1 summarizes the behavior with β = 0.95 for our data-set. Through of mean, variance, the intensity factor ( ), and maximum value we can define a threshold for normal behavior of . For instance, by averaging the means of and its maximum values during benign traffic, we can define an average threshold of 28.5 with a maximum of 114.8 units. We denoted these thresholds for each r by , , , and . Figure 1 shows the patterns and for benign traffic in Trace 5 and their variation are inside of stan- dard behavior mentioned above. 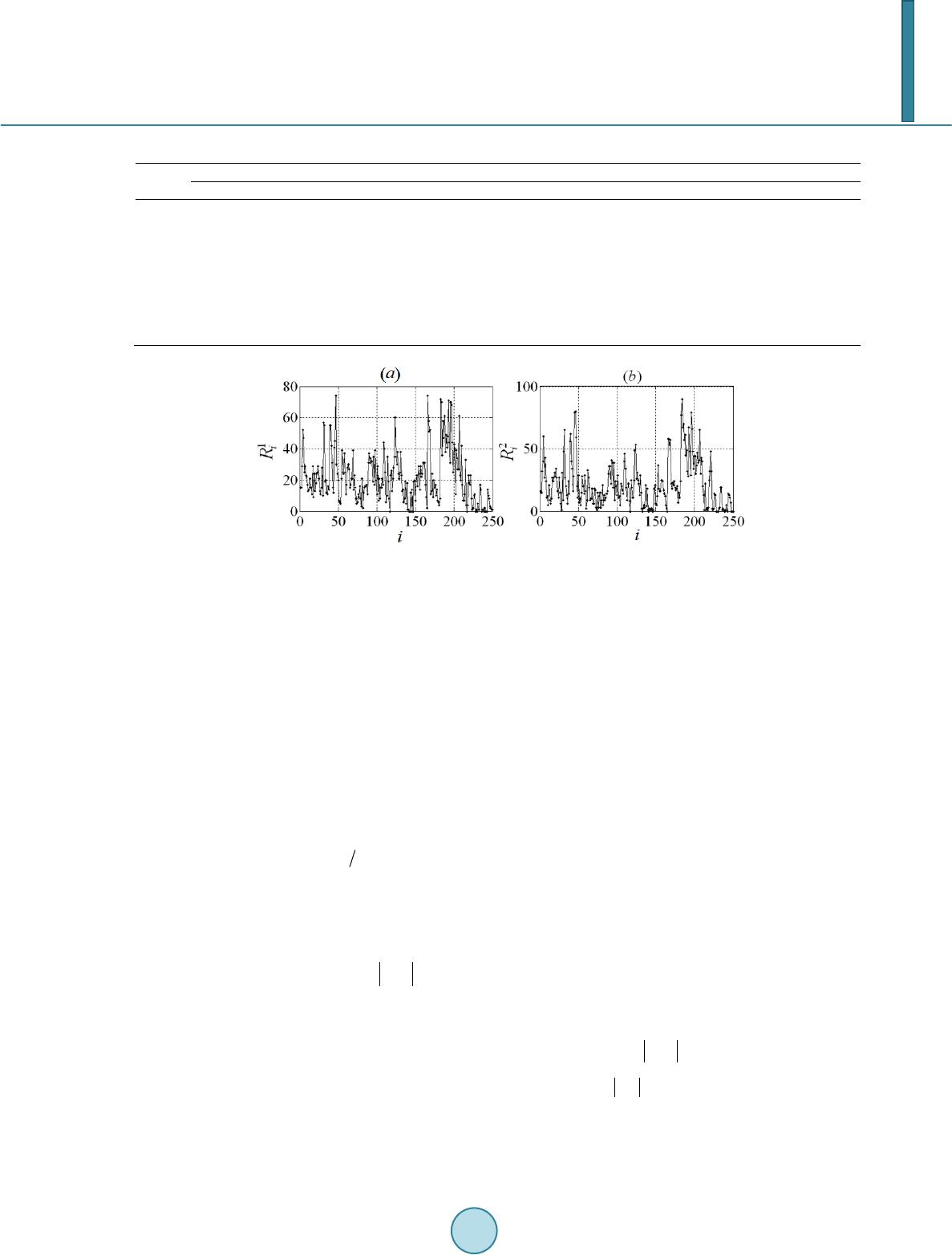 P. Velarde-Alvarado et al. Table 1. Values of mean, variance, and intensity factor for the rate of remnants. Trace 6-P1 14.5 1 6.6 76.1 74.5 145.1 166.8 4916 4958 10.0 1 0.05 64.6 66.53 Figure 1. Rate of remnants for (a) srcIP and (b) dstIP for standard traffic in Trace 5 in typical work hours. (td = 60 s, and β = 0.95). An anomaly related with a port scan attack directed to the proxy server was possible to detect it since the first slot that appeared (i.e . i = 2, 3) in trace 6-P1. The attack was carried out across a large number of TCP packets with source addresses supplanted. The growth of is possible to observe in Figure 2(a) and is far away from . patterns during worms attacks are presented in Figure 2(b) and Figure 2(c). There is a significant in- crease in the amount of remnants for r = 3 during the Blaster and Sasser Worm propagation. It is important to note that the anomaly detection is done from the earliest slots that the intrusion appears. 5. Three-Dimensional Spaces of Entropy The construction of a space of entropy is carried out at flow level, and through these spaces is possible to create profiles of behavior for the traffic of a network. Four three-dimensional spaces are generated for each one of the features extracted from the flows. We define a traffic trace χ of a duration tD seconds that is divided into M non-overlapping slots of seconds each one. In an i-slot flows are generated with a given in- ter-flow gap (IFG). All the flows for each slot are stored on indexed text files. The traffic features used in this technique are the flow’s fields and are identified as r = 1 for source IP address, r = 2 for destination IP address, r = 3 for source TCP port, and r = 4 for destination TCP port. Once that flows in an i-slot are generated, they should be clustering according to a r-flow feature. For instance, with a cluster key or pivot r = 1 the flows are aggregated into those flows that share the same source IP address. The number of clusters depends on , where is the alphabet set of all source IP addresses seen in the slot i. Thus, each cluster has flows with the same source IP address, but the rest of fields or features (r = 2, 3, 4) have freedom of variation. In this context, we can estimate the entropy for each r = 2, 3, 4 of each cluster. If we join these three values and associate them with a coordinate, we have a cloud of data points in a 3-D Eucli- dean space, where the axis are ( ) srcPrt dstPrt dstIP ˆ ˆ ˆ ,, HHH for r = 1. Finally, the points in the slot i, that is, ( ) srcPrtdstPrtdstIP 1 ˆ ˆ ˆ ,,HHH , ( ) srcPrtdstPrtdstIP 2 ˆ ˆ ˆ ,,HHH ,… ( ) srcPrt dstPrt dstIP1 ˆ ˆ ˆ ,, r i HHH = are plotted in the 3D-space. When we apply this procedure to the rest of cluster keys and all slots, we get four spaces of entropy. Figure 3 shows the spaces of entropy for three. First, in Figur e 3(a), we see the point pattern for Trace-1, which corresponds to normal traffic conditions being typical for Traces 1 - 5. Figure 3(b) and Figure 3(c) show 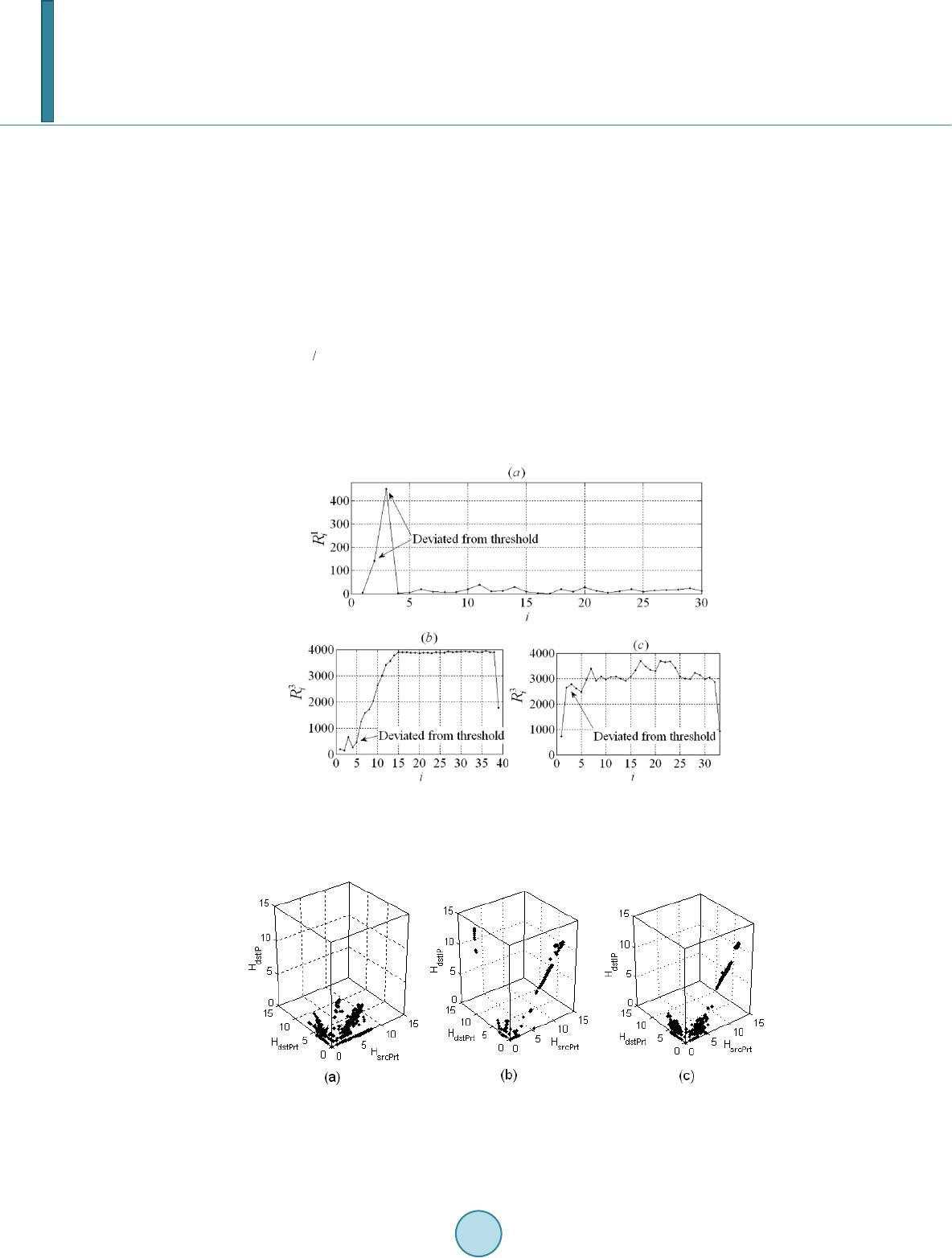 P. Velarde-Alvarado et al. a marked difference with regard to benign traffic, since the data points move away from positions typically ob- served. The characterization of the spaces of entropy represented by the vector for a cluster key r was rea- lized applying initially a technique of multivariable analysis, the Principal Component Analysis. PCA provides a roadmap for how reduce a complex data-set to a lower dimension to reveal the sometimes hidden, simplified structure that often underlie it. PCA is mathematically defined as an orthogonal linear trans- formation that transforms the data to a new coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component, PCA 1), the second greatest variance on the second coordinate, and so on, [12]. To obtain accurate analysis estimation, tools like Kernel Density Estimation (KDE) may be useful. This anal- ysis was applied on data-points at the slot level on the PCA 1 by using a Gaussian kernel of 200 points, with a bandwidth of , given by the Silverman’s criteria, where J is the number of observations and σ is the standard deviation of the set of observations. KDE shows that the traffic slots have Gaussian bimodality be- havior in its pdf. Each mode was labeled as principal mode and far mode respectively, as shown in Figure 4. Figure 4(a) shows that the densities of PCA 1 in benign traffic traces present a clear regularity in their shapes. This pattern of behavior changes drastically for anomalous traffic traces, see Figure 4(b) and F ig ure 4(c). Figure 2. Rate of remnant for: (a) srcIP, under port scan attack using spoofed IP addresses which is observable in slots i = 2 and i = 3 on Trace 6-P1 (b) srcPrt during Blaster Worm on Trace 6-P2. (c) srcPrt during Sasser Worm on Trace 6-P4. All cases td = 60 s and β = 0.95. Figure 3. Spaces of entropy for three srcIP cluster keys: (a) Traffic Trace-1 (benign traffic) in typical working hours. (b) Anomalous traffic, Trace 6-P2 (Blaster Worm) dur- ing 38 min period. (c) Anomalous traffic, Trace 6-P4 (Sasser Worm) during 38 min pe- riod. 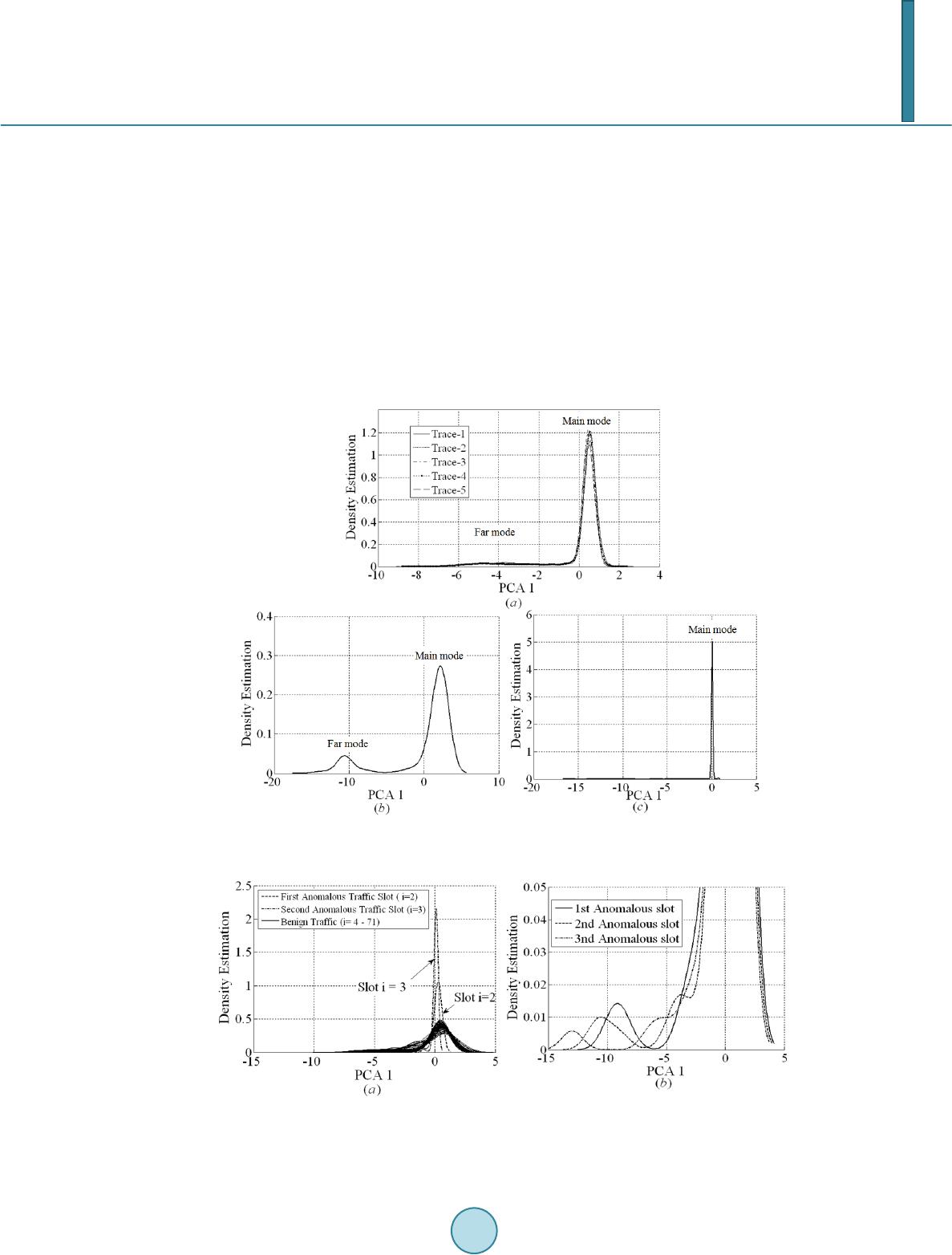 P. Velarde-Alvarado et al. This procedure was applied to i-slot level for a given r-, feature. The transformed data points are denoted by . Densities of under normal conditions presents bimodality, the second mode (far mode) is situated on the left side of the main mode, at an average of minus five units. On the other hand, the empirically calculated average variance of for benign traffic is three units. During analysis of the trace P1 was discovered that slots two and three had a variance of 0.32 and 0.74 units, respectively. These values are anomalous with regard to the threshold of three units. Thus, an anomaly (Figure 5(a)) was early detected in Trace 6-P1. The analysis of these traffic slots with Wireshark, was able to identify a port scan attack. In another case, Figure 5(b) shows the first three anomalous slots, where far mode moves away from the typ- ical value. The far mode displace to −9, −11 and −13 units, representing an anomaly with regard to the threshold of −5. This anomalous behavior in the far mode was caused by the spread of the Blaster worm. Similarly, the Sasser worm attack caused anomalous values in the variance of the transformed data-points, these anomalous values were close to 0.5 units. Figure 4. Kernel density estimation for PCA1 for: (a) Traces 1-5 (Benign Traffic), (b) Trace 6-P2 (Blaster attack), and (c) Trace 6-P4 (Sasser attack). Figure 5. Anomaly Detection on PCA1 (a) Anomaly caused by port scan detected in first slot in Trace 6-P1, (b) Anomaly caused by the Blaster worm that deviate the far mode out of the typical position.  P. Velarde-Alvarado et al. In all three cases studied, the attack leads to changes in traffic patterns that are detected from the first slots containing the malicious traffic. 6. Conclusions and Future Work The generation of behavioral profiles based on entropy offers an effective support for the Intrusion Detection Systems. The results of this study in a campus network show that under the Blaster and Sasser worm attacks as well as the port scanning, an A-NIDS employing profiles generated by the Rate of remnant elements or Three- Dimensional Spaces of Entropy methodologies can provide a rapid response detecting deviations from an estab- lished baseline in the early slots that the attack appears. As a future work, we will investigate the effect on variation of the slot duration td, smaller values of slot dura- tion represent faster response times, but also represent a smaller data set where to obtain representative traffic features, finding the optimum value is an important objective design. Acknowledgements This research was supported by the National Counsel of Science and Technology (CONACyT) of Mexico as part of the project SEP-2011 Ciencia Basica No. 167859. References [1] Fung, C. and Boutaba, R. (2013) Intrusion Detection Networks: A Key to Collaborative Security. Auerbach Publica- tions. [2] Kruegel, C., Valeur, F. and Vigna, G. (2005) Intrusion Detection and Correlation. Advances in Information Security. Springer. [3] Xu, K., Zhang, Z. and Bhattacharyya, S. (2005) Profiling Internet Backbone Traffic: Behavior Models and Applica- tions. SIGCOMM, 2005, 22-26 . [4] Nucci, A. and Bannerman, S. (2007) Controlled Chaos. IEEE Spectrum, 44, 42-48. http://dx.doi.org/10.1109/MSPEC.2007.4390022 [5] V elarde-Alvarado, P., Vargas-Rosales, C., Torres-Roman, D. and Munoz-Rodriguez, D. (2008 ) Entropy Based Analy- sis of Worm Attacks in a Local Network. Research in Computing Science, 34, 225-235. [6] Copley, D., Has sell , R., Jack, B., Lynn, K., Permeh, R. and Soeder, D. (2003) ANALYSIS: Blaster Worm. eEye Digi- tal Security Research. http://research.eeye.com/html/advisories/published/AL20030811.html [7] Ukai, Y. and Soeder, D. (2004) ANALYSIS: Sasser. eEye Digital Security Research. http://research.eeye.com/html/advisories/published/AD20040501.html [8] Jacobson, V., Leres, C. and McCanne, S. Tcpdump/libpcap. http://www.tcpdump.org/ [9] A. Peppo, plab. Tool for Traffic Traces. http://www.grid.unina.it/software/Plab/ [10] Trac Project. Libtrace. h ttp://www.wand.net.nz/trac/libtrace [11] E. Kohler, ipsumdump. Traffic tool. http://www.cs.ucla.edu/~kohler/ipsumdump [12] Jolliffe, I.T. (2002) Principal Component Analysis, Series: Springer Series in Statistics. 2nd Edition, Springer, XXIX, 487 pp. 28.
|