 Journal of Computer and Communications, 2014, 2, 1-14 Published Online September 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.211001 How to cite this paper: Coleman, T.F. and Li, Y.Y. (2014) A Graduated Nonconvex Regularization for Sparse High Dimen- sional Model Estimation. Journal of Computer and Communications, 2, 1-14. http://dx.doi.org/10.4236/jcc .2014.211001 A Graduated Nonconvex Regularization for Sparse High Dimensional Model Estimation Thomas F. Coleman, Yuying Li 1Departmentof Combinatorics and Optimization, University of Waterloo, Waterloo, Canada 2Cheriton School of Computer Science, University of Waterloo, Waterloo, Canada Email: tfcol eman @u water loo. ca , yuying@uwaterloo.ca Received May 2014 Abstract Many high dimensional data mining problems can be formulated as minimizing an empirical loss function with a penalty proportional to the number of variables required to describe a model. We propose a graduated non-convexification method to facilitate tracking of a global minimizer of this problem. We prove that under some conditions the proposed regularization problem using the continuous piecewise linear approximation is equivalent to the original regularization problem. In addition, a family of graduated nonconvex approximations are proposed to approximate its continuous approximation. Computational results are presented to illustrate the performance. Keywords Sparse Model Estimation, Variable Selectio n Regu l arizati on 1. Introduction Sparsity is a desired property in model estimation since it often leads to better interpretability and out-of-sample predictability. In [1], a risk bound is established for the model selection by minimizing the empirical loss func- tion penalized by the number of variables needed to describe the model. In this context, model dimension is the number of unknown variables; sparsity refers to a small number of variables selected to define the model. Thus sparse model estimation is also sometimes referred to as variable selection. Selecting a model with a small number variables can be formulated as minimizing an empirical loss function with a penalization for the number of nonzero variables; this is referred to as -regularization. Unfortunately this is a NP-hard global optimization problem, see, e.g., [2] [3]. Relaxation of cardinality regularization has long been used as a way to approach the sparse model selection problem, see, e.g., [4] [5]. Due to its computational simplicity, regularization based on the norm is popular in practice. This is referred to as ridge regression. It has also long been recognized that regularization often leads to sparsity in solutions, see, e.g., [6]-[11] [29]. Recent compressive sensing theory, e.g., [12]-[14]), formally establishes that, under a certain restricted isometry property (RIP) on a sensing matrix , a sparse vector can be reconstructed ex- actly from . In addition, computational methods have been developed to obtain solutions efficiently, see, e.g. , [15]-[17].  T. F. Coleman, Y. Y. Li Despite its success, the regularization approach can potentially lead to model bias for model estimations, see, e.g., [18]-[21]. In [18], a smoothly clipped absolute deviation (SCAD) penalty is proposed using a noncon- vex regularization to avoid the potential bias. Iterative methods are proposed in [23] [24] to approximate a local minimizer of the SCAD penalized loss. It is proposed in [18] that a proper regularization function for model es- timation should be chosen with three objectives: avoid bias in the resulting estimator, achieve sparsi ty in the es- timated model, and, finally, achieve continuity or stability in model prediction. The regularization function is able to achieve sparsity and smoothness but can lead to model bias. In addition, using regularization does not always lead to the sparsest model which fits the data to a specified accuracy. Recently computational meth- ods have also been proposed to iteratively solve regularization problems, see, e.g., [25] [26]. The main objective of this paper is to devise a computational method to minimize the empirical loss function with a penalization for the number of nonzero variables. We approximate the counting indicator function by a continuous piecewise linear function. We show mathematically that a continuous piecewise linear approxima- tion has appealing theoretical properties. To facilitate tracking a global minimizer, this continuous piecewise function is further approximated by a family of continuously differentiable piecewise quadratic functions which are indexed by a parameter controlling the degree of nonconvexity in the approximation. Starting from an initial convex function, a sequence of increasingly more nonconvex approximate problems are solved, using the solu- tion to the previous problem as a starting point for the next approximate problem. In addition, each approxima- tion can be regarded as a regularization function for model estimation; each approximation behaves similar to the function near the origin (ensuring sparsity), the function asymptotically (avoiding bias), and con- tinuously differentiable everywhere (for smoothness). We illustrate the efficacy of the proposed method in de- termining a sparse model for data fitting, computational efficiency of the approach, and the effect of the pa- rameters on the gradual non-convex approximations. 2. Continuous Approximation to Assume that measures the empirical error based on the given data. We want to solve the following regularization problem ( ) ( ) 1 min n n i xR i fx x µ ∈= +Λ ∑ (2.1) whe r e the counting indicator function is ( ) 1 if 0 0 otherwise i i x x≠ Λ= and is a penalty parameter, balancing the objectives of minimization of and sparsity in the solu- tion. Unfortunately standard optimization methods cannot be applied to the data fitting problem (2.1) since the car- dinality function is discontinuous and nonconvex. Convex relaxations have been proposed for (2.1), see, e.g., [5] [27]; these relaxations can be sub-optimal since (2.1) is nonconvex. In [28] the counting indicator is approximated, in the context of image processing, by the piecewise quadratic and solves ( ) ( ) 1 ˆ min n n i xR i fxh x λ µ ∈= + ∑ (2.2) whe r e ( ) 2 1 if ˆ 1 otherwise zz hz λ λλ ≤ = and is a small resolution parameter. We propose to approximate the discontinuous counting indicator function by the following continuous penalty function , ( ) 1 if 1 otherwise zz hz λ λλ ≤ = 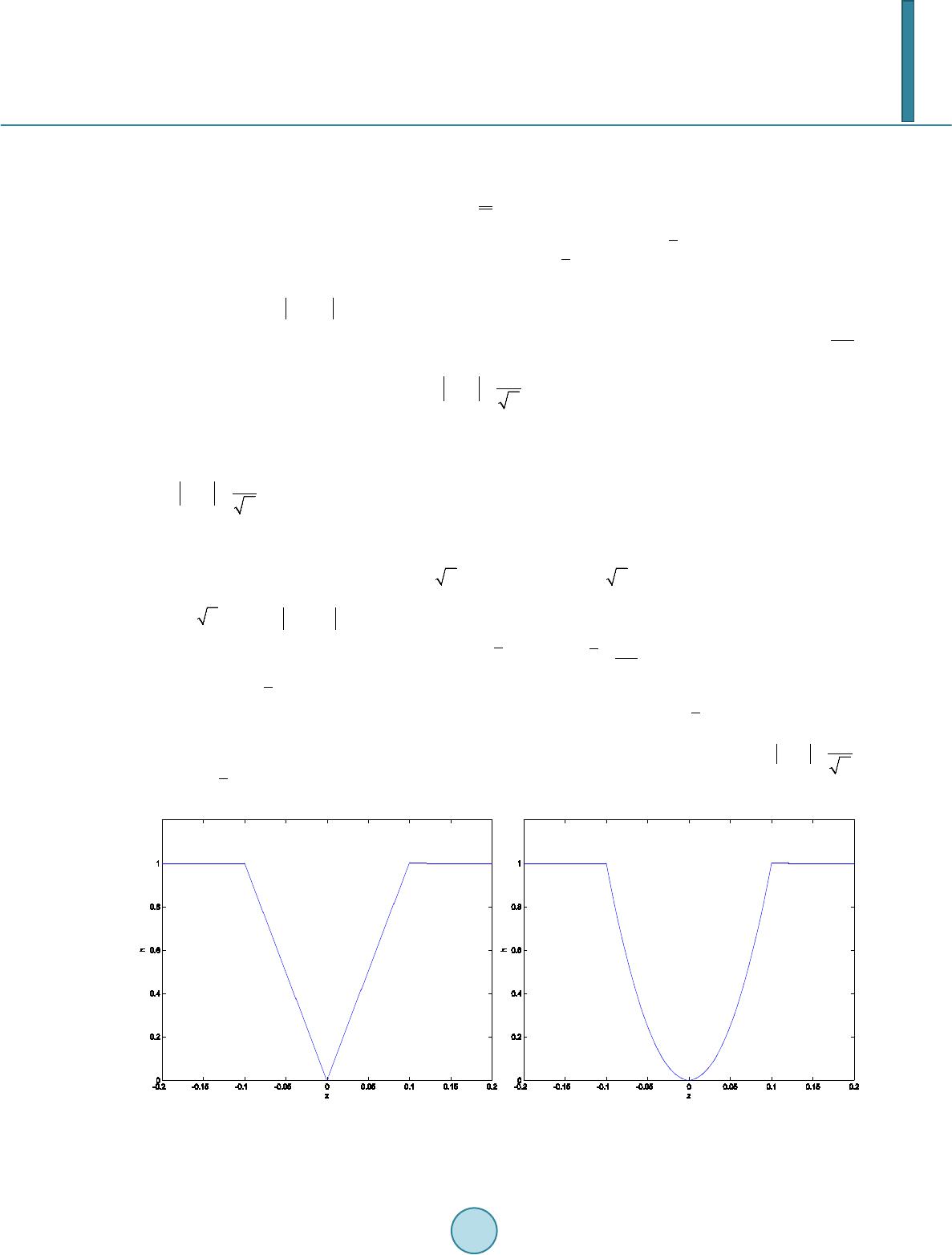 T. F. Coleman, Y. Y. Li Figure 1 illustrates and Usin g , the regularization problem (2.1) is approximated by ()() ( ) def 1 min ; n n i xR i pxf xhx λ λµ ∈= + ∑ (2.3) Next we establish mathematically that there exists a finite threshold parameter such that a solution to (2.3) is a solution to the original penalty problem (2.1) for all . Assumption 2.1. Assume is twice continuously differentiable on an open set and there ex- ists such that for all , . Lemma 2.1. Suppose Assumption 2.1 holds. Let be a local minimizer of with , Then, for each index , either or . Hence either or for Proof. For notational simplicity, in this proof, we denote . simply as . Suppose the contrary, i.e., for some index i, . We note that in this situation the derivative of with respect to exists at be- cause is everywhere differentiable on and since by assumption∗is not a cusp point, is also differentiable at . Then, by local optimality , i.e., ( ) ( ) ( ) ( ) 0 or 0 ii ii fx fx µλ µλ ∗∗ ∇+=∇−= But , which is contradictory. Lemma 2.2. Let be a local minimizer for for some . Then is a local minimizer of . Proof. Suppose that is not a local minimizer of for some . Lemma 2.1 states that the components of are partitioned into two sets: i.e., for each indexeither or . Since , the same partition applies with respect to . Therefore Figure 1. Quadratic (left subplot) and piecewise linear (right sunplot) approximations to the counting indicator function with λ = 100.  T. F. Coleman, Y. Y. Li ( )( ) 11 () () nn ii ii hxh x λλ + ∗∗ = = = ∑∑ It follows from the definition for that cannot be a minimizer of , a contradiction. Theorem 2.1. If is a strong local minimizer for for some . Then is a local minimizer of ( )( ) ( ) 1i n i pxf xx µ = =+Λ ∑ . Proof. By Lemma 2.2, is a local minimizer of for all sufficiently large. We show that is a local minimizer of by contradiction. Suppose that∗is not a local minimizer of . Then there exists a sequence converging to and . This implies that for sufficiently large . Since, for sufficiently large , And , we have that This contradicts that∗is a strong local minimizer of for some . If one uses to approximate , a minimizer to the approximation problem (2.2) will gener- ally not be a minimizer to the regularization problem (2.1) unless either or , which typically does not hold for any . Theorem 2.1 indicate that our proposed approximation is supe- rior to in solving the regularization problem (2.1). 3. Graduated Non-Convex ification We now address a couple of additional challenges. Firstly, is not differentiable everywhere, which is also the case for . Secondly, is not convex; thus problem (2.3) has many local minimizers. Ass ume . Consider the following ( ) minsubject tox0, n i xR fx i ∈ = ∈ (3.1) Then any local minimizer of (3.1) is a local minimizer of (2.1) for a fixed . For a given , computing a global minimizer of the regularization problem (2.1), or the proposed approximation (2.3), is NP-hard. However, the quality of the estimated model depends on being able to find, as much as possible, a sufficiently good approximation to the global minimizer of (2.1). Next we develop a com- putational method to produce a good approximation to the global minimizer of the piecewise linear minimiza- tion problem (2.3). Assume that the empirical loss function is convex. Hence the nonconvexity comes from the counting indicator function. In [28], a graduated non-convexification process is proposed, in the context of image processing, in an attempt to find the global minimizer of the piece- wise quadratic approximation (2.2) as follows. The continuous function is approximated using a family of continuously differentiable piecewise quadratic functions , where ( ) 2 2 ˆ(; )1 2 1 otherwise zif z g zzifz λ λκ ρ ρ γκγ ≤ =−−≤≤ (3.2) (3.3) Here is a parameter indexing the family of approximations to . The function is a piece wise quadratic, with the concave quadratic 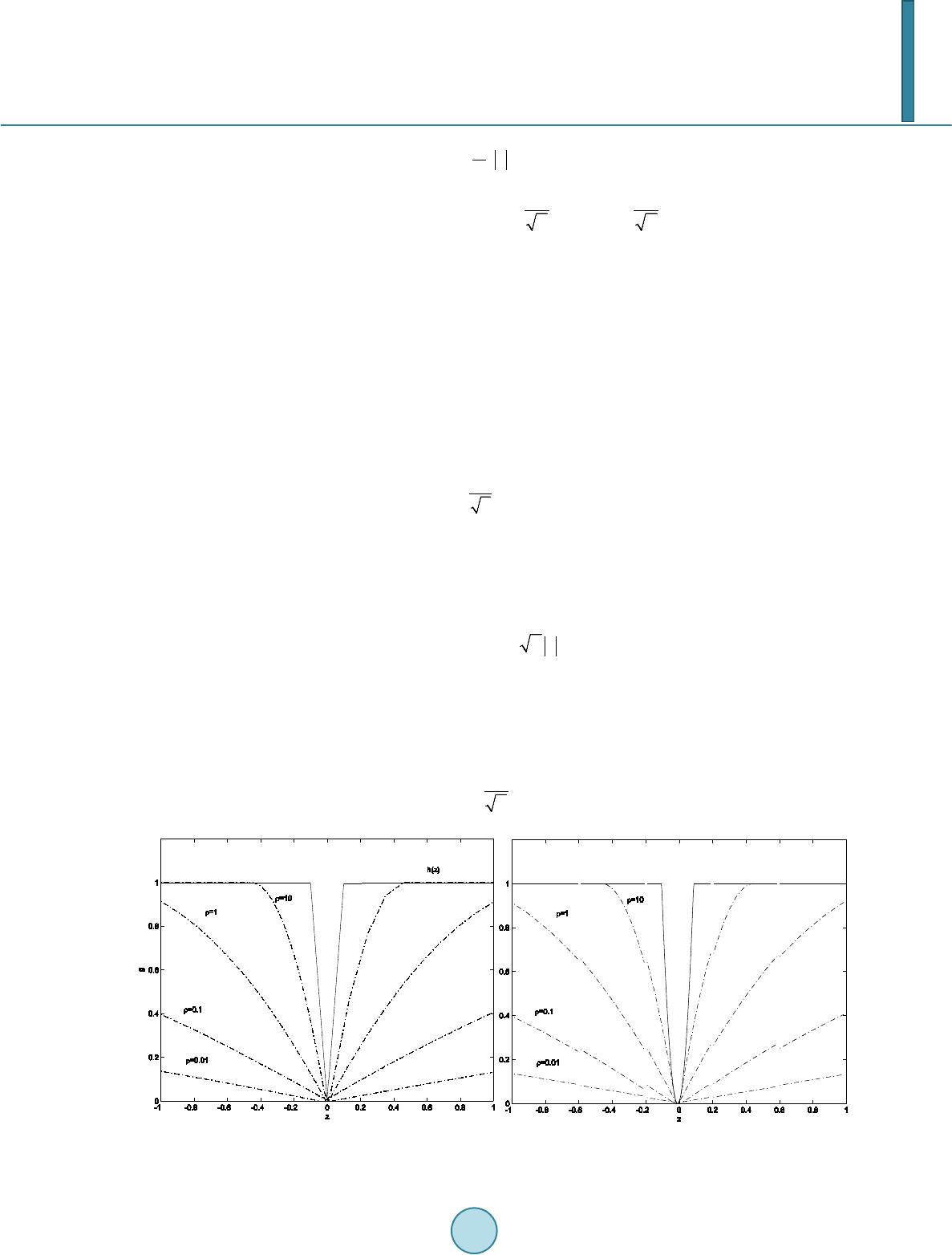 T. F. Coleman, Y. Y. Li when . Note that, for any , we have . Thus . In addition the function is continuously differentiable and symmetric with respect to . Left subplot in Figure 2 graphically illustrates the function . Substituting for , we have () () 1 ˆ min ; n n i xR i fxg x λ µρ ∈= + ∑ (3.4) Let be a given monotonically increasing sequence which converges to . In [28], the global mini- mizer of the piecewise quadratic minimization (2.2) is tracked by solving a sequence of problems (3.4) indexed by a monotonically increasing sequence , using the solution of the th problem as the starting point for the kth problem. Initially, the minimizer for the empirical error function, which corresponds to (3.4) with , is computed. As , , and . Thus problem (3.4) approaches the minimization of the empirical error function min as . As increases, the second order derivative of the quadratic function in equals , which becomes increasingly more negative, gradually introducing non-convexity. In addition, as , and the function approaches . Geo- metrically, the convex empirical error function is gradually deformed to the concave function, with the- computed solution sequence following a path from the minimizer of to, ideally, the global minimizer of . Similarly we can design a family of approximations to track the global minimizer of in (2.3). For sparsity, we want to retain the segment in a neighborhood of . Outside this neighborhood, we require the approximation to be continuously differentiable. Finally, similar to , we ensure that this approximation gradually approaches the piecewise linear . Based on in (3.2), we construct a family of approximations for with the desired properties as follows. Let and be defined in (3.3). First we select two break points and so that and . In addition, and monotonically increase to as converges to ; this property also holds Figure 2. Graduated nonconvex approximation (left subplot) and (right subplot).  T. F. Coleman, Y. Y. Li for . Then we construct the unique quadratic spline on : ( )() ( ) 1 2 when when sz z Sz sz z ξη ηκ ≤≤ =≤≤ which satisfies the following boundary conditions: the function values and the derivative values at and are given by and respectively, i.e., ()( ) ()( )()( ) 2 11 , , 1, . 2 SS SS ξξξ γγ ρ κκγκ ρκγ ′ = = ′ =− −=−− (3.5) We now approximate the nondifferentiable piecewise linear functi on when by the fol- lowing continuously differentiable function below: () () () ( ) 1 2 2 1if if ;if 1 if 2 1 otherwise zz sz z gz sz z zz λ ξ γ ζη ρηκ ργκγ ≤ ≤≤ =≤≤ − −≤≤ (3.6) where and are defined in (3.3). Subplot (b) in Figure 2 graphically illustrates the function . By construction, is an even function. In addition, it is continuously differentiable on . We now establish the monotonicity property for whe n . Lemma 3.1. Let be the quadratic spline in with the breakpoints and the boundary conditions (3.5) restated below ( )( ) ( )()( )() 2 11 , , 1, . 2 SS SS ξξξ γγ ρ κκγκ ρκγ ′ = = ′ =− −=−− where and κare defined in (3.3). Assume and . Then is strictly monotonically increasing on and is strictly monotonically increasing on . Proof. Assume that ()() ( ) 2 1 111 sza bzcz ξξ =+−+− and ( )( )( ) 2 2 222 sza bzcz ξξ =+−+− are the quad- ratics. For the spline on with the boundary conditions (3.5), we have , and . The boundary conditions (3.5) imply that ( )( ) ( )()( )() 1111 2 22 22 11 ,, 1, . 2 as bs as bs ξξ ξ γγ ρ κκ γκργκ ′ = == = ′ = =−−= =− (3.7) The derivative and function continuity of the spline at yields () ( ) ()( )( )( ) 21 12 22 12212 1 , 2 . bb cc ccaab b ηξ ηκ ηξηκηκ ηξ − −− −= −−−= −+− −−  T. F. Coleman, Y. Y. Li This leads to ()()() ()()( ) 21 212 1 12 2 bb aab b c ηκ ηξκη ηξ κηηξ − −+− −−+− =− +−− . Since is continuous at , ( )() 2 22 ˆ;as g λ κκ ρλκ = == . Using (3.3), . Let ,. From , using (3.7), and , ( )( ) 211 1 12aabb κξκξ γ −= −= −=∆ Since is continuously differentiable at , using (3.7), we have . Hence () () 21 1 3bb b ηκ ηξ − −− =−∆ . Using above, , and , we obtain () ()( ) 21 212 11 1 22 bb aab bb ηκ ηξκη − −+− −−+−=−∆ . From the value of and the above, we have Hence ( )() 1 111 1 2 0. 2 s bcb η ηξ ′=+−= > Since and are linear in and respectively, from ( )( )() 1 12 0, 0s ss ξ ηη ′ ′′ >=> and , we conclude that and are strictly monotonically increasing in and . Since and are strictly monotonically increasing in and respectively, we conclude that is monotonically increasing in . Figure 2 compares the approximation with the approximation for a few values of . Left and right subplots visually look very similar. However, the main difference can be seen near . Replacing by , we obtain: ( ) ( ) 1 min ; n n i xR i fxg x λ µρ ∈= + ∑ (3.8) Each approximation can be considered as a regularization for the empirical function mini- mization. This penalty function corresponds to the penalty around for ; it behaves like the count- ing indicator function when is very large. The size of each region depends on the parameter . When , the penalty is used in and the counting indicator function is used in . For any given , the penalty function is continuously differentiable everywhere except at the origin. The func- tion is piecewise quadratic with a concave quadratic piece for . 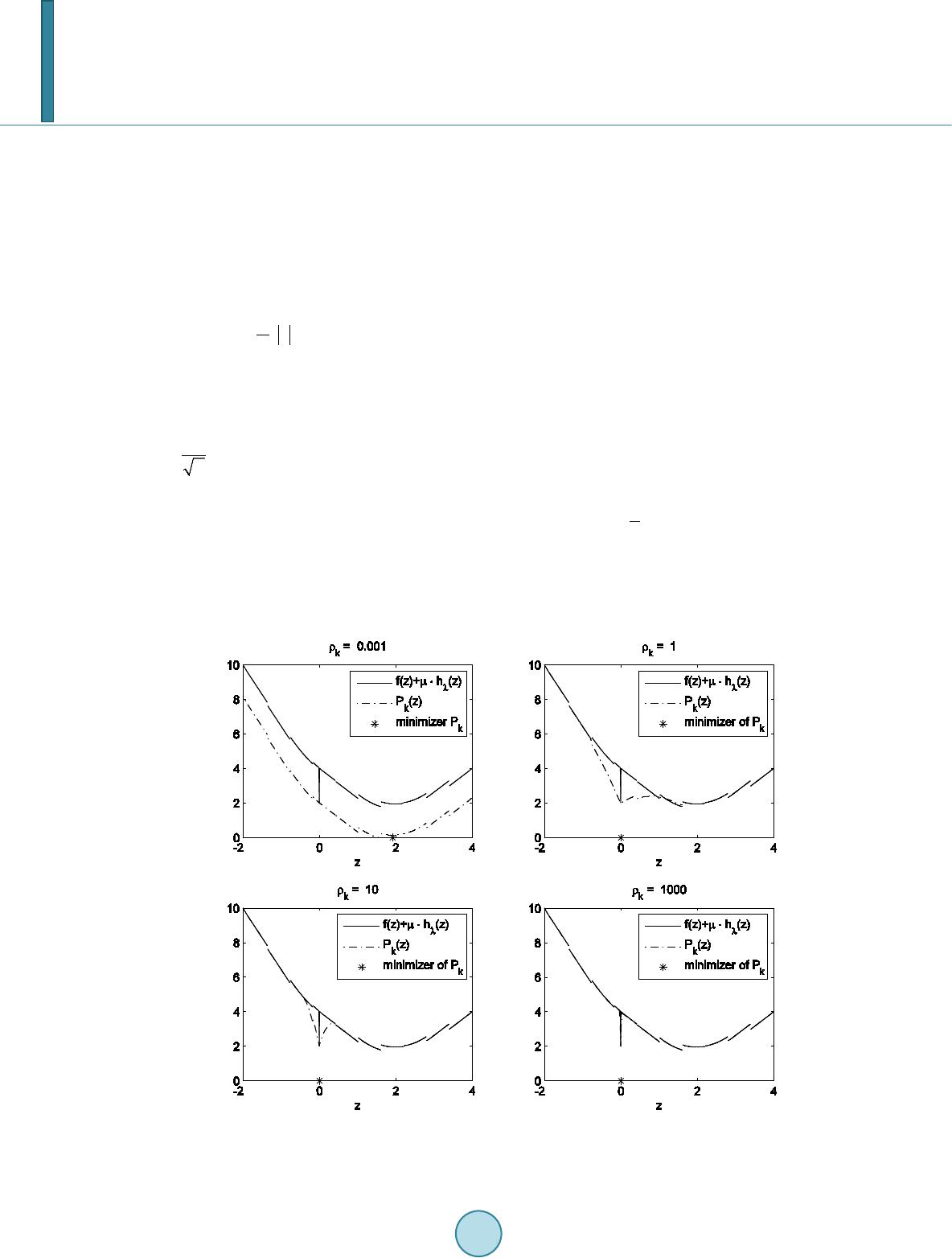 T. F. Coleman, Y. Y. Li Based on (3.8), a gradual nonconvexification process can similarly be applied to track the global minimizer of (2.3), and (2.1) if is sufficiently large. Assume that the empirical function is convex. For notational simplicit y, let ( )( ) ( ) 1 ; n k ik i Pxfxgx λ µρ = =+ ∑ (3.9) Starting from the minimizer of , a sequence of approximations to the penalized empirical error mini- mization problem (3.8), is solved by approximating the indicator function. As converges to zero, , and all converge to zero and converges to . Thus approaches the quad- ratic segment with the (negative) curvature converging to zero. Hence the optimization problem (3.8) approaches the empirical error function minimization as approaches zero. As increases, the cur- vature of the quadratic function defining for becomes more negative, introducing a graduated nonconvexity. The negative curvature interacts with the positive curvature of the empirical error func- tion in an attempt to reach the optimal subset solutions via minimizing . In addition, as , , and the functions approach . Figure 3 graphically illustrates how this graduated nonconvexification process tracks the global minimizer of the minimization problem (2.3) with an one-dimensional function . In the top-left subplot of Figure 3, we see the original nonconvex function , a convex approximation (corresponding to ), and its minimizer. Increasing to 1, we see the next approximation to the original function in the top-right subplot. With the minimizer of the first approximation function as a starting point, the minimizer of the new approximation, which is very close to the global minimizer, is computed. In the bottom two subplots Figure 3. Tracking the global minimizer of : Graduated nonconvex approxima- tions.  T. F. Coleman, Y. Y. Li ( and 1000 respectively), we see how the approximating functions approach the original func- tion as increases. From this illustration we see that the proposed process first considers large scale features of the function and gradually focuses in on features of a smaller scale. This graduated noncon- vexification process can be terminated when the approximation to is sufficiently accurate at the computed solution. Next Theorem 3.1 shows that when, for all either or , accu- rately approximates at the computed solution and remains so for any larger . Theorem 3.1. Assume that and are defined in (3.3), , and and are monotonically increasing functions of . Then the following holds: • If the first order necessary condition for (3.8) is satisfied at with and either or , then the first order optimality condition for (3.8) is satisfied at for any . • If the second order necessary condition for (3.8) is satisfied at with and either or , then the second order optimality condition for (3.8) is satisfied at for any . Proof. Assu me that and either or for . By definition (3.3), and for .From the monotonicity assumption of and , for , and . Therefore, ( )( )( )( ) 22 000 0 ;;, and ;;. iii i nnn n iiii xxx x gx gxgxgx λλλ λ ρρρ ρ ∗∗∗ ∗ ∗∗∗∗ ≠≠≠ ≠ ∇=∇∇=∇ ∑∑∑ ∑ Hence the first order and the second order necessary conditions for (3.7) hold at with , when these conditions for (3.7) hold at wit h . Applying Theorem 3.1, the following can be used as a stopping condition for the graduated nonconvexifica- tion process: ( )( ) either or , ik ik kk x xi ξγ ∗∗ < >∀ (3.10) We also note that only can be erroneous in approximating in . Thus when is sufficientl y small, we can also regard this approximation as sufficiently accurate. Thus, the computation can also terminate if the region of the inaccuracy becomes sufficiently small. The proposed graduated non-convex approximation process is summarized in Figure 4. 4. Computational Results In this section we illustrate the performance of the proposed computational methods for mode estimation. We assume that the variables are constrained to be nonnegative; we note that the illustrated properties of the pro- posed sequence of approximations to regularization on sparsity will be similar when the model parame- ters are unconstrained. To illustrate, we generate random sparse model selection problems based on least squares data fitting prob- lems below: GNC1 Algorithm. Let be a large constant and be a monotonically increasing sequence which converges to . Lettolbe a positive stopping tolerance. 1) Compute a minimizer for minimization problem (3.8) with the penalty parameter . Let . 2) Compute a solution to (3.8) with using the computed solution of (3.8) with as a starting point. 3) If either (3.10) or the inequality holds, terminate. Otherwise, and go to the step 1). Figure 4. A graduated nonconvexification method for the sparse model selection.  T. F. Coleman, Y. Y. Li ( ) 2 2 01 1 min 2 n i xi Ax bx µ = ≥ −+ Λ ∑ (4.1) Each random problem instance is generated by a random matrix where is an -by- random orthogonal matrix, is an -by- random orthogonal matrix, and is a random diagonal ma- trix with a condition number equal to a specified constant. The -by-1 vector is set to equal to where is a random vector with nonzero components (randomly selected); the nonzero components equal . Here ra nd is a random sample from the uniform distribution in . The vector is a vector of independent standard normal with a standard deviation equal to , unless stated otherwise. Using the graduated nonconvexification algorithm, we compute a solution to (4.1) by solving a sequence of approximations below: ( ) 2 2 01 1 min ; 2 n ik xi Ax bgx λ µρ ≥= −+ ∑ (4.2) where is a sequence of monotonically increasing positive numbers. Unless stated otherwise, we set , , and . In addition, we let the spline breakpoints be as follows: 1 1 0.5min,0.5, 1 1 0.25min,0.5. ξκ ρ ηκ ρ = − = − We refer to the computational algorithm in Figure 4 with the specified parameter setting above as GNC1. We use the trust region algorithm for bound constrained problems proposed in [30] to solve (4.2). We illustrate various properties of the computed model . Specifically we report empirical error, sparsity, and errors com- pared to the true model used to generate data. In measuring sparsity, we regard a component as zero if . In addition, we assess the approximation error of using the continuous approximation or to the indicator function at the computed solution . We also evaluate the computational cost of the graduated nonco n ve xi fic ati o n process and report the total number of optimization iterations required to obtain the estimate and the average number of optimization iterations required for minimizing each . Specifically, based on 100 random problem instances, we report the following attributes based on the average values from 100 random problem instances: • Empirical error: • Average relative distance to the true model: • Sparsity: the number of zeroes in the computed solution , i.e., . • Accuracy in approximating the counting indicator function by or : recall that the ap- proximation is accurate if implies that . Thus we measure this accuracy by ( ) 6 1 1 ˆ10 1 ˆ n i i n i i x x λ − = = Λ≤ Λ≤ √ ∑ ∑ ; value 1 means 100% accuracy. • Average number of optimization iterations over all . • Total number of optimization iterations for the entire gradual non-convexification process: . Table 1 reports the performance assessment for GNC1based on the piecewise linear approximation to the counting function in the specified parameter setting. The number of observationsequals 200 and the dimension of equals 100. Two subpanels correspond to the number of nonzeros in , equals to 50 and 90 respectively. The column under provides the properties of the least squares solution  T. F. Coleman, Y. Y. Li for the given data; we see that the average least squares error is approximately 0.1. As the penalty parameter increases, the average data fitting error increases but sparsity in the estimate also increases from 0 to about 70. In addition observe from Table 1 that there is little difference in the fitting error when but the sparsity in the solution estimate is drastically different, from no zero components to more than 35 when the true solution has about 50 zero components, i.e., . From Table 1, we also observe that the relative average distance to the true parameter is smaller than that of the least squares solution, when the penalty parameter is for which estimate is fairly sparse. This indicates that sparsity regularization is indeed important in accurate model estimation. We also note that the error in using to approximate the counting indicator function at the computed estimate is very small with a minimum correctness of 80% for penalty parameter ; complete accuracy of 100% is achieved when . One potential concern of the proposed graduated non-convex me thod is the computational cost since a poten- tially large sequence (corresponding to the parameter sequence of optimization problems need to be solved. However, since for each minimization of , the solution from is used as a starting point, the to- tal number of optimization iterations required is quite reasonable. For example, when , on average a total of 77.31 iterations are required to compute for the entire GNC1 process. Since the average number of iterations for minimizing is 4.83, this implies that the GNC1 process here terminates after about 16 steps on average. It can be observed that the total number of iterations required increases with the penalty parameter . We also investigate performance for the underdetermined data fitting problems; the number of observations is less than the number of unknown variables (specifically and ). Table 2 illustrates that the relative distance to the true model is significantly larger in the underdetermined case than in the over de- termined case; the corresponding entries in Table 1 are included in Table 2 for comparison. This is reasonable since there is less information available to infer the true model. Table 1. GNC1 performance statistics from 100 random problems with the number of observations m greater than the di- mension n: with = 1e-005 and . Number of nonzeros in the generator K = 50 m = 200 n = 100 0.098 0.108 0.111 0.257 2.380 0.199 0.172 0.188 0.469 0.686 0.000 20.610 35.020 53.480 68.700 ( ) () 6 ˆ|10 ˆ|1 i i i i x x λ − Λ≤ Λ≤ ∑ ∑ 0.000 0.812 0.942 1.000 1.000 0.000 2.123 4.832 7.947 7.281 0.000 33.970 77.320 127.150 116.490 Number of nonzeros in the generator K* = 90 m = 200 n = 100 0.099 0.102 0.103 0.309 2.831 0.160 0.150 0.177 0.485 0.694 0.000 5.260 9.820 31.140 53.660 ( ) ( ) 6 ˆ || 10 ˆ | |1 i i i i x x λ − Λ≤ Λ≤ ∑ ∑ 0.000 0.805 0.948 1.000 1.000 0.000 2.023 3.094 7.353 8.368 0.000 32.370 49.510 117.650 133.890  T. F. Coleman, Y. Y. Li Table 2. Distance to the true model (GNC1): overdetermined vs u nderd etermined , with = 1e-005 and . Distance to the True Model: µ = 0 1e-006 0.0001 0.01 1 (m,n) Number of nonzeros in the generator K* = 50 (200,100) 0.199 0.172 0.188 0.469 0.686 (100 200) 0.720 0.714 0.715 0.781 0.857 (m,n) Number of nonzeros in the generator K* = 90 (200,100) 0.160 0.150 0.177 0.485 0.694 (100 200) 0.722 0.718 0.721 0.784 0.861 5. Conclud ing Remarks In high dimensional data fitting problems, the objective is to minimize an empirical loss function based on data while achieving sparsity in the model parameters at the same time. Achieving sparsity can be crucial in obtain- ing robust out-of-sample performance and attaining meaningful understanding of the causal relationship in data. In addition, sparsity may be an explicit goal in practical applications such as tracking market indices with a s mall number of assets. The combination of minimizing empirical loss and maximizing sparsity naturally leads to a minimization problem regularized by a penalty, which is proportional to the number of variables describing the model to be estimated, this problem with many local minimizers. The empirical loss function is often convex. Assuming this property, we propose a graduated non-convex al- gorithm to minimize a convex empirical loss function regularized with a penalty proportional to the number of nonzero variables. The proposed algorithm is based on approximating the counting indicator function by a continuous piecewise linear function. We show mathematically that the continuous piecewise linear approximation to the counting in- dicator function has more attractive properties than the continuous piecewise quadratic approximation. Specifi- cally, there exists a sufficiently large parameter so that the regularized optimization problem using this ap- proximation is equivalent to the original optimization problem regularized by the number of nonzero in the model parameters. This property does not hold for the continuous piecewise quadratic approximation. A graduated nonconvexification process is proposed by introducing a family of approximations to the con- tinuo us piecewise linear function. This family of approximations is indexed by a nonnegative parameter . In addition, these approximations can be regarded as penalty functions themselves with the following properties. Firstly there is a region around the origin in which the penalty function is the penalty. In another region, the penalty function equals counting indicator functions. As ρ increases, both regions increases and the region with penalty converges to and the region with the counting indicator function as penalty converges to . In addition, for any , the penalty function is continuously differentiable everywhere except at the origin. Each penalty function is an even function with a monotonicity property. When the parameter is small, a small negative curvature is added to the convex empirical loss funct io n to form a regularized objective function. As ρ increases, more negative curvature is added but the region in which the penalty is nonconvex shri nk s. We investigate performance of the proposed graduated nonconvexification algorithm based on randomly gen- erated least squares problems with different sparsity levels in the true solution We observe that the data fit- ting error increases as the penalty parameter μ increases. Simultaneously sparsity in the computed solution in- creases as the penalty increases. In addition, sparse solutions (with sparsity close to the true solutions) can be  T. F. Coleman, Y. Y. Li computed without much compromise in the magnitude of the data fitting error. Indeed, the solution with the smallest relative distance to the true solution is obtained by sparse solutions with the sparsity close to that of the true solutions. Our results also indicate that the computational costs required by the GNC process is relatively moderate, since the computed solution in the kth step in the graduate nonconvexification process is often a good starting point for the (k+1)th step. References [1] Barron, A., Birge, L. and Massart, P. (1999) Risk Bounds for Model Selection via P enali zation. Probability Theory and Related Fields, 113 , 301 -302. http://dx.doi.org/10.1007/s004400050210 [2] Natarajan, B.K. (1995 ) Sparse Approximate Solutions to Linear Systems. SIAM Journal on Computing, 24, 227-234. http://dx.doi.org/10.1137/S0097539792240406 [3] Davis, G. , Mallat, S. and Avellaneda, M. (1997) Greedy Adaptive Approximation. Constructive Approximation, 13, 57-98. http://dx.doi.org/10.1007/BF02678430 [4] Tropp, J.A. (2006) Just Relax: Convex Programming Methods for Identifying Sparse Signals in Noise. IEEE Transac- tions on Information Theory, 52, 1030-1051. [5] Tropp, J.A. (2004) Just Relax: Convex Programming Methods for Subset Selection and Sparse Approximation. Tech. Rep. ICES Report 0404, The University of Texas at Austin. [6] Taylor, H.L., Banks, S.C. and McCoy, J. F. (1979) Deconvolution with the l1 No r m. Geophysics, 44, 39-52. http://dx.doi.org/10.1190/1.1440921 [7] Levy, S. and Fullagar, P.K. (1981) Reconstruction of a Sparse Spike Train from a Portion of Its Spectrum and Applica- tion to High -Resolution Deconvolution. Geophysics, 46, 1235 -12 43. http://dx.doi.org/10.1190/1.1441261 [8] Wu, J.K. (1994 ) Two Problems of Computer Mechanics Program System. In: Proceedings of Finite Element Analysis and CAD, Peking University Press, Beijing, 9-15. [9] Santosa, F. and Symes, W.W. (1986) Linear Inversion of Band -Limited Reflection Seismograms. SIAM Journal on Scientific and Statistical Computing, 7, 1307-1330. http://dx.doi.org/10.1137/0907087 [10] Li, Y. and Santosa, F. (1996) A Computational Algorithm for Minimizing Total Variation in Image Restoration. IEEE Transactions on Image Processing, 5, 987-995. http://dx.doi.org/10.1109/83.503914 [11] Coleman, T.F., Li, Y. and Mariano, A. (2001) Segmentation of Pulmonary Nodule Image Using 1-Norm Minimization. Computational Optimization and Application, 19, 243-272. [12] Donoho, D.L., Elad, M. and Temlyakov, V.N. (2006) Stable Recovery of Sparse Overcomplete Representations in the Presence of Noise. IEEE Transactions on Information Theory, 52, 6-17. http://dx.doi.org/10.1109/TIT.2005.860430 [13] Candès, E.J. (2006) Compressive Sampling. In: Proceedings of the International Congress of Mathematics, Madrid, Spain . [14] Candés, E.J., Romberg, J. and Tao, T. (2006) Robust Uncertain ty Princip les: Exact Signal Reconstruction from Highl y Incomplete Frequency Information. IEEE Transactions on Information Theory, 52, 489-509. http://dx.doi.org/10.1109/TIT.2005.862083 [15] Kim, S., Koh, K., Boyd, S. and Gorinvesky, D. (2007) An Interior Point Method for Lar ge-S cale l1 Regularized Least Squ ares. IEEE Journal on Selected Topics in Signal Processing, 1, 606-617. http://dx.doi.org/10.1109/JSTSP.2007.910971 [16] Wright, S.J., Nowak, R.D. and Figueiredo, M. A. T. (2009) Sparse Reconstruction by Separable Approximation. IEEE Transactions on Signal Processing, 57, 2470-2493. http://dx.doi.org/10.1109/TSP.2009.2016892 [17] Daubechies, I., Devore, R., Fornasier, M. and Güntürk, C.S. (2009) Iteratively Re-Weighted Least Squares Minimiza- tion for Sparse Recovery. Communications on Pure and Applied Mathematics LXIII (2010) 0001-0038, 2470-2493. [18] Fan, J. and Li, R. (2001) Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. Jour nal of the American Statistical Association, 96, 1348-13 60. http://dx.doi.org/10.1109/TSP.2009.2016892 [19] Fan, J. and Li, R. (2006) Statistical Challenges with High Dimensionality: Feature Selection in Knowledge Discovery. In: Sanz-Sole, M., Soria, J., Carona, J.L. and V erd era, J., Eds., Proceedings of the International Congress of Math e- matics, 595-622. [20] Lv, J. and Fan, Y. (2009) A Unified Approach to Model Selection and Sparse Recovery Using Regularized Least Squ ares. The Annals of Statistics, 37, 3498-3528. http://dx.doi.org/10.1214/09-AOS683 [21] Fan, J., Lv, J. and Qi, L. (2011) Sparse High Dimensional Models in Econ omics. Annual Review of Economics, 3, 291 - 317.  T. F. Coleman, Y. Y. Li [22] Fan, J. (1997) Comments on “Wavelets in Statistics: A R evie w”. Journal of the Italian Statistical Society, 6, 131-138. http://dx.doi.org/10.1007/BF03178906 [23] Hunter, D.R. and Li, R. (2005) Variable Selection Using mm Algorithms. The Annals of Statistics, 33, 1617-1642. http://dx.doi.org/10.1214/009053605000000200 [24] Zhou, H. and Li, R. (2008) On e -Step Sparse Estimates in Nonconvex Penalized Likelihood Models (with Discussi on). The Annals of Statistics, 36, 1509-1533. http://dx.doi.org/10.1214/009053607000000802 [25] Cand´es, E.J., Wakin, M.B. and Boyd, S.P. (2008) Enhancing Sparsity by Reweighted l1 Minimization. J. FourierAna Appl, 14, 877-905. http://dx.doi.org/10.1007/s00041-008-9045 -x [26] Chartrand, R. and Yin , W. (20 08 ) Iteratively Reweighted Algorithms for Compressive Sensing. In: IEEE International Conference on Acoustics, Speech and Signal Processin g, 3869-3872. [27] Zhang, T. (2010) Analysis of Multi-Stage Convex Relaxation for Sparse Regularization. Journal of Machine Learning Research , 10, 1081-11 07. [28] Blake, A. and Zisserman, A. (1987) Visual Reconstruction. Cambridge. [29] Coleman, T.F ., Henninger, J. and Li, Y. (2006) M inimizing Tracking Error While Restricting the Number of Asse t s . Journal of Risk, 8, 35-56. [30] Coleman, T.F. and Li, Y. (1996) An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM Journal on Optimization, 6, 418-445. http://dx.doi.org/10.1137/0806023
|