Energy and Power En gi neering, 2011, 3, 167-173
doi:10.4236/epe.2011.32021 Published Online May 2011 (http://www.SciRP.org/journal/epe)
Numerical Research of Heat Transfer of Supercritical
CO2 in Channels
Lina Zhang1, Minshan Liu2, Qiwu Dong2, Songwei Zhao2
1School of Aeronautics Engineering, Zhengzhou Institute of Aeronautical Industry Management,
Zhengzhou, China
2Thermal Energy Engineering Research Centre, Zhengzhou University, Zhengzhou, China
Received December 17, 2010; revised March 18, 2011; accepted April 13, 2011
Abstract
With the worldwide development of nuclear power plant and requirement of saving energy and resource,
high thermal efficiency and economical competitiveness are achieved by using supercritical CO2 with special
thermal properties and better flow and heat transfer characters. In this paper, heat transfer of supercritical
CO2 has been investigated in square and triangle array tube-bundle of cooled system in reactor using compu-
tational fluid dynamics (CFD) code FLUENT, and the basic knowledge of heat transfer of supercritical CO2
and first experience of CFD simulation are obtained. The effect of mesh structures, turbulence models, as
well as flow channel size is analyzed. The choice of turbulence model adopted in simulating supercritical
CO2 is recommended. Comparing the effect of heat transfer with supercritical CO2 and supercritical water as
cooled medium, the results show that the former was higher. The new idea is provided for choice of cooled
medium and improving thermal efficiency this paper.
Keywords: Nuclear Power, Supercritical CO2, Heat Transfer, Numerical Analysis
1. Introduction
Supercritical fluids are very popular in a number of in-
dustrial applications because of their special thermal
properties, such as advanced water-cooled nuclear reac-
tors, environmentally friendly air-conditioning and re-
frigeration systems and high pressure water oxidation
plant for waste processing. Recently, carbon dioxide has
been used frequently in experimental studies because of
its lower critical pressure and temperature. A compre-
hensive understanding of the flow and heat transfer
characteristic of supercritical fluid is essential for the
purpose of performing accurate thermal-hydraulic pre-
dictions, which is important in supercritical light water
reactor (SCLWR) design calculations. At the same time,
heat transfer of supercritical fluids is studied by using
computational fluid dynamics (CFD) codes for predict-
ing the heat transfer coefficient and providing a better
understanding of the heat transfer mechanism.
Kim et al. [1] researched the heat transfer of super-
critical carbon dioxide flowing upward through tubes and
a narrow annulus passage by experiments. S. M. Liao
and T. S. Zhao [2] studied convective heat transfer to
supercritical carbon dioxide in miniature tubes with di-
ameters of 0.70, 1.40, and 2.16 mm. The results of ex-
periments revealed that the buoyancy effects were sig-
nificant for all the flow orientations, although Reynolds
numbers were as high as 105. Chaobin Dang and Eiji
Hihara [3] investigated experimentally heat transfer of
supercritical carbon dioxide cooled in four horizontal
cooling tubes with different inner diameters ranging from
1 to 6mm. M. Sharabi [4] et al. investigated the effect of
different turbulent models on the simulation results of
supercritical CO2 in triangular and square channels.
The used turbulence models included RNG k-ε model
and six kinds of low Reynolds number formulations.
Pei-Xue Jiang et al. [5] investigated convection heat
transfer of supercritical CO2 in a 0.27 mm diameter ver-
tical mini-tube experimentally and numerically. Lixin
Cheng et al. [6] analyzed and compared many reports of
heat transfer and pressure drop experimental data and
correlations for supercritical CO2 cooling in-macro- and
micro-channels.
The large variation of the fluid physical properties of
CO2 at 8 MPa with temperature around the critical point
influences heat transfer strongly as shown in Figure 1.

168 L. N. ZHANG ET AL.
The temperature at which the specific heat at constant
pressure attains a maximum value is called the pseudo
critical temperature, TPC. The important characteristics of
fluids at supercritical pressure, which makes them very
particular from the point of heat transfer, is that their
specific heat vary rapidly with both pressure and tem-
perature, as seen from Figure 2.
Although a large number of numerical studies on heat
transfer of supercritical fluids have been carried out by
various authors, these works are mostly concentrated to
simple geometries which are usually circle tubes. The
objective of this study is to figureure out the distinctive
characteristics of supercritical heat transfer in various
flow channels such as triangular tube and sub channels of
rod bundles using the CFD code FLUENT.
2. Turbulent Models and Method of Solution
Three kinds of low Reynolds number turbulent models
are considered including YS model, LS model and AKN
model provided by FLUENT code. The low-Reynolds
number turbulent models respond strongly to the effects
of buoyancy and acceleration resulting from the sharp
decrease in density with the increase of temperature due
to heating and the subsequent redistribution of velocity
in the near wall region, and exhibit severe localized dete-
rioration of heat transfer. The model equations are as
following:
Continuity

0
t
  
V (1)
Momentum
 
P
t



 

VVV Vg
 (2)
Energy
 
p
TT
tC



 



VT


(3)
where ρ, μ, λ and CP are density, dynamic viscosity,
thermal conductivity and specific heat for fluid, respec-
tively, V and g are the dimensional velocity vector and
gravity vector, t is time, and T is temperature.
Turbulent kinetic energy (k) [7]:


2
1/2
2
it
ij kj
k
ku kk
txx x
k
Gn
 

 

 




 





 


(4)
Dissipation rate (ε):
Figure 1. Properties near pseudo-critical temperature.
Figure 2. Specific he at wi th bulk fluid te mperature.



2
22
1
12 22
2
it
ij j
t
k
u
txx x
Cu
Gf Cf
kk
n


  

 


 




 





 




(5)
where
2
t
k
Cf



 (6)
The effect of gravity and buoyancy is considered. The
QUICK scheme was used for approximating the convec-
tion terms in the momentum. Inlet is mass flow boundary
condition, inlet fluid temperature and pressure are pro-
vided to define the inlet. Pressure outlet boundary condi-
tion is used for the outlet. SIMPLEC algorithm is
adopted for pressure-velocity coupling, which is particu-
larly recommended for the case of buoyant. The second
order QUICK scheme is used for discretization of mo-
mentum, energy and turbulence equations. The carbon

L. N. ZHANG ET AL.
169
dioxide is pressurized to 8 MPa. Inlet fluid temperature
is 288.15 K.
3. Triangular Channel
To gather first experience in the application of CFD
codes to supercritical fluids, a vertically oriented trian-
gular channel was selected which studied experimental
by Jong Kyu Kim, et al. [8]. The structure size, boundary
conditions (symm represents symmetrical condition) and
grid adopted in the simulation of the model is illustrated
as Figure 3. Due to symmetry, only a half of the actual
flow passage is modeled for the triangular channel. The
hydraulic diameter is 9.8 mm and the heated length is 1.2
m. The sections before and after the heated section were
500 mm long (more than 40 d). Calculations with various
size counts, which are 80 × (80 × 40), 100 × (100 × 50)
and 120 × (120 × 60) in the axial directions and the OB
side and OC side of the radial directions along the heated
length, showed that the results were independent of the
three kinds of size counts of grid. Therefore, the meshes
with 100 size counts in the axial direction and (100 × 50)
size counts in the radial direction were used. The con-
vergence criteria required a decrease of at least six orders
of magnitude for the residuals with no observable change
in the surface temperatures for an additional 200 itera-
tions.
Figure 4 shows the triangular duct wall temperatures
predicted by the three kinds of low Reynolds number
turbulent models under heat flux of 50 kW/m2 and mass
flux of 419 kg/(m2s). In the study, computational simula-
tions were compared with the selected experiments re-
ported by Jong Kyu Kim et al. [8]. As can be seen, the
simulations have the same trend with the experiment.
The wall temperature appears a peak near Z/Dh equal to
20. Thereafter, the wall temperature decreases slightly as
Z/Dh increases, as a result of the change in fluid transport
properties. The results of different turbulent models are
almost same. The AKN turbulence model over-predicts
significantly turbulence reduction, and the result is same
with S. He et al. [9].
In the later simulation of this paper, modeling results
will be reported using the AKN because the results in-
dependent on the grid numbers can easily obtained ac-
cording AKN turbulence model.
Figure 5 shows local Nusselt number variations in tri-
angular tube along the flow direction, and the correla-
tions and experimental data with the present simulated
data are compared. The simulated data are very close to
the experimental data during the heated section, and are
in reasonably good agreement with the two correlations.
Kransnoshchekov and Protopopov’s and Jackson’s cor-
relations are based primarily on the forced convection at
C
O
wall
wall
symm
B
Figure 3. Grid and boundary conditions adopted for the
triangular channel.
Figure 4. Wall temperature along the axial line C.
Figure 5. Local Nusselt number variations in the flow di-
rection.

170 L. N. ZHANG ET AL.
supercritical pressure. Other forced convection correla-
tions for heating CO2 in a vertical pipe have been pro-
posed, but according to Jackson and Hall, Krans-
noshchekov and Protopopov’s correlation is the most
accurate and is supported by the most experimental data
[8].
The effect of mesh structures and turbulence models
was studied. Based on a comparison of the numerical
results with experimental data, the accuracy and applica-
bility of turbulence models were assessed.
Figure 6 shows the wall temperature variations for the
triangular channel in the axial direction at the different
heat flux, with the mass flux is 314 kg/(m2s). There is a
peak in the temperature distribution, it shows the heat
transfer deterioration. The deterioration takes place ear-
lier at about Z/Dh equal to 10 under higher heat flux
equal to 40 kW/m2. The heat transfer deterioration takes
place stronger under higher heat flux.
The distributions of Nusselt number along heated sec-
tion under different heat flux are as shown in Figure 7. It
is noted that the Nusselt number fluctuates to some ex-
tent. Nusselt number appears a peak under higher heat
flux, and the heat transfer deterioration takes place ear-
lier. Nusselt number appears two peaks under 20 kW/m2.
4. Sub-Channels
In this section, sub-channels of both triangular-array and
square-array rod bundles are taken, the structure and grid
as indicated in Figure 8, and the simulated parameters
are as Table 1.
Nusselt numbers for forced convection are calculated
by using the Gnielinski correlation [10]:
 

2/3
8Re1000 Pr
1.0712.78 Pr1
b
b
f
Nu f


b

(7)

2
10
1.82log Re1.64
b
f
 
 (8)
Figure 9 shows the Nusselt number of supercritical
CO2 and water in the square array rod bundles under
pressure of 8 MPa and 25 MPa respectively. The mass
flux and the heat flux of water are 740 kg/(m2s) and 600
kW/m2 respectively, and those of CO2 are 300 kg/(m2s)
and 100 kW/m2, respectively. The simulated data of su-
percritical water are cited from numerical analysis re-
ported by X. Cheng et al. [11]. Supercritical CO2 under
far lower pressure, mass flux and heat flux, the Nusselt
number is little lower than supercritical water. The effect
of heat transfer with supercritical CO2 is better than that
of supercritical water.
Figure 10 and Figure 11 show the effect of mass flux
on Nusselt number as a function of fluid bulk tempera-
ture (Tb) of square and triangular array rod bundles, and
Figure 6. Wall temperature along the axial line C.
Figure 7. Local Nusselt number variations in the flow di-
rection.
Figure 8. Grid structure and boundary conditions.

L. N. ZHANG ET AL.
171
Table 1. Parameters for the sub channels simulation.
Parameters Range
Rod bundle arrangement Square, triangular
Rod diameter 8.0 mm
Pitch-to-diameter ratio 1.2
Pressure 8 MPa
Mass flux 200 - 300 kg/(m2s)
Heat flux 60 - 100 kW/m2
Fluid bulk temperature 280 - 350 K
Turbulence models AKN
Figure 9. Variation of Nusselt number for supercritical CO2
and water.
Figure 10. Mass flux effects on Nusselt number in square
array rod bundle.
Figure 11. Mass flux effects on Nusselt number in triangu-
lar array rod bundle.
Tin equals to 288.15 K, heat flux is 100 kW/m2. The
mass flux effects Nusselt number significantly due to the
increased Reynolds number. However, before the critical
point, mass flux has less effect on heat transfer. The peak
values increase with increasing mass flux. The peak of
Nusselt number appears around the pseudocritical tem-
perature. After the near-critical point region, the effect of
mass flux on Nusselt number becomes more obvious.
Figure 12 shows the effect of heat flux on the Nusselt
number as a function of bulk temperature in the square
array rod bundles. Before the pseudocritical temperature,
the Nusselt number under different heat flux is nearly
same. With the increasing bulk temperature, the variety
becomes more obvious. Especially under lower heat flux,
the Nusselt number decreases significantly.
Figure 13 shows the comparison between the square
lattice and triangular lattice of Nusselt number along
bulk temperature with the heat flux 100 kW/m2. The heat
transfer is enhanced in the triangular lattice at pseudo-
critical temperature and got cross that temperature, and
the reason is that the degree of turbulence increases be-
cause of the change of structure of flow channels.
5. Conclusions
Heat transfer of supercritical CO2 has been investigated
in various flow channels. Three kinds of low Reynolds
number turbulent models are adopted to analyze the ef-
fect on the wall temperature of the triangle channels, and
the results show that difference under different turbulent
models is rather small, and then AKN turbulent model
are chosen.
In triangular channels, the wall temperature increases

172 L. N. ZHANG ET AL.
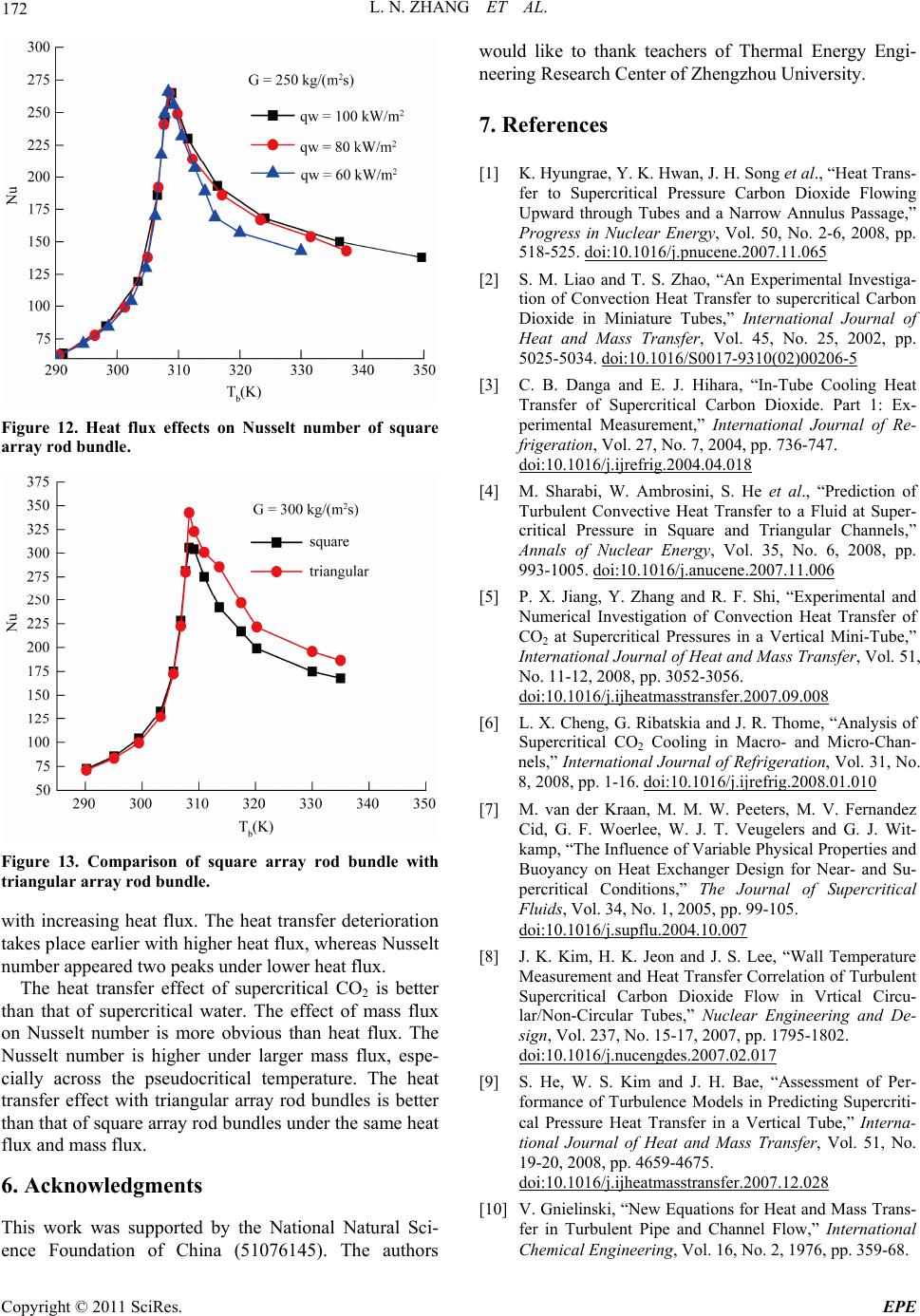
Figure 12. Heat flux effects on Nusselt number of square
array rod bundle.
Figure 13. Comparison of square array rod bundle with
triangular array rod bundle.
with increasing heat flux. The heat transfer deterioration
takes place earlier with higher heat flux, whereas Nusselt
number appeared two peaks under lower heat flux.
The heat transfer effect of supercritical CO2 is better
than that of supercritical water. The effect of mass flux
on Nusselt number is more obvious than heat flux. The
Nusselt number is higher under larger mass flux, espe-
cially across the pseudocritical temperature. The heat
transfer effect with triangular array rod bundles is better
than that of square array rod bundles under the same heat
flux and mass flux.
6. Acknowledgments
This work was supported by the National Natural Sci-
ence Foundation of China (51076145). The authors
would like to thank teachers of Thermal Energy Engi-
neering Research Center of Zhengzhou University.
7. References
[1] K. Hyungrae, Y. K. Hwan, J. H. Song et al., “Heat Trans-
fer to Supercritical Pressure Carbon Dioxide Flowing
Upward through Tubes and a Narrow Annulus Passage,”
Progress in Nuclear Energy, Vol. 50, No. 2-6, 2008, pp.
518-525. doi:10.1016/j.pnucene.2007.11.065
[2] S. M. Liao and T. S. Zhao, “An Experimental Investiga-
tion of Convection Heat Transfer to supercritical Carbon
Dioxide in Miniature Tubes,” International Journal of
Heat and Mass Transfer, Vol. 45, No. 25, 2002, pp.
5025-5034. doi:10.1016/S0017-9310(02)00206-5
[3] C. B. Danga and E. J. Hihara, “In-Tube Cooling Heat
Transfer of Supercritical Carbon Dioxide. Part 1: Ex-
perimental Measurement,” International Journal of Re-
frigeration, Vol. 27, No. 7, 2004, pp. 736-747.
doi:10.1016/j.ijrefrig.2004.04.018
[4] M. Sharabi, W. Ambrosini, S. He et al., “Prediction of
Turbulent Convective Heat Transfer to a Fluid at Super-
critical Pressure in Square and Triangular Channels,”
Annals of Nuclear Energy, Vol. 35, No. 6, 2008, pp.
993-1005. doi:10.1016/j.anucene.2007.11.006
[5] P. X. Jiang, Y. Zhang and R. F. Shi, “Experimental and
Numerical Investigation of Convection Heat Transfer of
CO2 at Supercritical Pressures in a Vertical Mini-Tube,”
International Journal of Heat and Mass Transfer, Vol. 51,
No. 11-12, 2008, pp. 3052-3056.
doi:10.1016/j.ijheatmasstransfer.2007.09.008
[6] L. X. Cheng, G. Ribatskia and J. R. Thome, “Analysis of
Supercritical CO2 Cooling in Macro- and Micro-Chan-
nels,” International Journal of Refrigeration, Vol. 31, No.
8, 2008, pp. 1-16. doi:10.1016/j.ijrefrig.2008.01.010
[7] M. van der Kraan, M. M. W. Peeters, M. V. Fernandez
Cid, G. F. Woerlee, W. J. T. Veugelers and G. J. Wit-
kamp, “The Influence of Variable Physical Properties and
Buoyancy on Heat Exchanger Design for Near- and Su-
percritical Conditions,” The Journal of Supercritical
Fluids, Vol. 34, No. 1, 2005, pp. 99-105.
doi:10.1016/j.supflu.2004.10.007
[8] J. K. Kim, H. K. Jeon and J. S. Lee, “Wall Temperature
Measurement and Heat Transfer Correlation of Turbulent
Supercritical Carbon Dioxide Flow in Vrtical Circu-
lar/Non-Circular Tubes,” Nuclear Engineering and De-
sign, Vol. 237, No. 15-17, 2007, pp. 1795-1802.
doi:10.1016/j.nucengdes.2007.02.017
[9] S. He, W. S. Kim and J. H. Bae, “Assessment of Per-
formance of Turbulence Models in Predicting Supercriti-
cal Pressure Heat Transfer in a Vertical Tube,” Interna-
tional Journal of Heat and Mass Transfer, Vol. 51, No.
19-20, 2008, pp. 4659-4675.
doi:10.1016/j.ijheatmasstransfer.2007.12.028
[10] V. Gnielinski, “New Equations for Heat and Mass Trans-
fer in Turbulent Pipe and Channel Flow,” International
Chemical Engineering, Vol. 16, No. 2, 1976, pp. 359-68.

L. N. ZHANG ET AL.
173
[11] X. Cheng, B. Kuang and Y. H. Yang, “Numerical Analy-
sis of Heat Transfer in Supercritical Water Cooled Flow
Channels,” Nuclear Engineering and Design, Vol. 237,
No. 3, 2007, pp. 240-252.
doi:10.1016/j.nucengdes.2006.06.011