 Open Journal of Social Sciences, 2014, 2, 186-192 Published Online September 2014 in SciRes. http://www.scirp.org/journal/jss http://dx.doi.org/10.4236/jss.2014.29032 How to cite this paper: Wang, Y., Wu, L.H. and Shao, H.Y. (2014) Clusters Merging Method for Short Texts Clustering. Open Journal of Social Sciences, 2, 186-192. http://dx.doi.org/10.4236/jss.2014.29032 Clusters Merging Method for Short Texts Clustering Yu Wang, Lihui Wu, Hongyu Shao School of Management Science an d Engineering, Dalian University of Technology, Dalian, China Email: ywang@dlut.edu.cn, 876520946@qq.com, hong-yu-8@163.com Received April 2014 Abstract Under push of Mobile Internet, new social media such as microblog, we chat, ques ti on answ eri ng systems are constantly emerging. They produce huge amounts of short texts which bring forward new challenges to text clustering. In response to the features of large amount and dynamic growth of short texts, a two-stage clustering method was putted forward. This method adopted a sliding window slid ing on the flow of short texts. Inside the slide window, hierarchical clustering method was used, and between the sli d e windows, clusters me rgi ng method based on information gain was adopted . Experiment indicated that t his me thod is fast a nd has a higher accuracy. Keywords Short Texts Clustering, Slide Wind ow, Information Gain, Hierarchical Clustering 1. Introduction Mobile Intern et er a has arrived with th e widespread use of mobile devices, especially smartphones. The in- creasing amount of data genera t ed by mobile Internet is bringing new challenges and opportunitie s to da ta anal- ysis, especially to data mining. Social medias based on mobile Internet like we chat, micro-blog, twitter and other applications have become increasingly popular, which produce a larg e number of information every day. The key here is that most of the information is appeared in the form of short text. In addition, user-interactive question answering system has attracted more and more attentions, with the rapid development of Web2.0. However, in these inter activ e systems, there are a large number of similar or duplicate information, which are generally short and co lloquial. The wide range emergen ce of short texts on the Internet has proposed new re- quirements to existing text clustering methods. By cluster analysis, we can get hot news, organize short texts ef- fectively, and bu ild automated question answering systems. Different from traditional text cluster ing , short text clustering is usually of the following characteristics [1]: (1) Grow dynamically. Wechat, microblog and other emerging social medias have a rapid gr owth r ate, but al- so have high real-time requirements on clustering results. (2) Text is short. Usually there are fewer words in short texts, for example, Sina Weibo requires each message is no more than 140 words. This feature makes short texts fewer text features. (3) Language is more casual, and there are many spoken language, abbreviations, new words, even spelling errors.  Y. Wang et al. (4) The number of short texts is huge, usually at least one million. Traditional text clustering methods are mainly segmentation methods and hierarchical clustering methods. The main idea of segmentation methods is to optimize existing clusters through different subdivision strate- gies. K-means algorithm is a typical segmentation algorithm [2], and it selects initial point as cluster center to continually iterate. K-means algorithm is easy to understand, easy to implement and is of a high efficiency. However, before starting to cluster, we must first specify the number of clusters, which is difficult to implement for large -scale dynamic growth short text data. Hierarchical clustering algorit hm [3] can be divided into hierarchical clustering an d div isiv e hier archical clustering bas ed on clustering direction. It does not need to specify the number of clusters, but its time complex- ity is O(n 3). So it cannot be applied to large-scale short t ext clustering. For the text feature representation, traditional methods often use vector space model (VSM). The methods cannot extract all the features for short text expre s sio n. In addition, because terms in short texts are not standard, the results of segmentation are un satisf actory. On this basis, Zhao Pen g et al. [4] applied HowNet on the text semantic representation, so that the documents with the same theme can be merged. In recent years, clustering algorithms for short texts are constantly raised. J ilian g Ta ng et al. [5] proposed a multi-language representation method for short texts u s ing machine translation, extended text representation, and solved some problems like polysemes, synonyms and insufficient statistical information. Wang et al. [6] proposed an extension of vector space model for communication short te xts, called WR-KMeans. Pengze Ying [7] found a short text clustering phenomenon by analyzing results of short texts clustering, which is called long-tail phenomenon. They applied long-tail phenomenon on clustering, removed some unnecessary clustering operations, and proposed an incomplete clustering method. Chen Jianchao [8] proposed an improved CBC algo- rithm, which adaptiv ely determined the center of each cluster in its to tality. A ll th e methods are mainly focused on how to carry out feature representation and similarity calculation of short texts, while th e c luster ing perfor- mance is not much improved. This paper proposed a two-stage clustering method for dynamically increasing short texts. By windows slid- ing on the text streams, data inside the window performed hierarchical clustering, then similar clusters were merged on the re su lts of hierarchical clustering between windows. 2. Two-Stage Clustering Method For larg e-scale sh or t tex ts , this paper decomposed them for enhancing clu ster e fficiently. F ig ur e 1 shows the process of clustering. In this method, a sliding window slides successively in those data which have not been clustered. It controls the number of objects to be clustered by setting the size of sliding window. It is hard to determine the number of clusters before clustering, so we choose agglomeration hierarchical clustering method. The drawback of hierar- Figure 1. Two -stage clustering process.  Y. Wang et al. chical clustering method in time complexity can be overcome by setting a smaller size of sliding window. Clas- sical vector space model is applied in short text representation. In order to improve the accuracy of segmentation, we need to add user dictionary and ne twork w or ds to segmentatio n dic tionar y in the process. In the two-stage clust ering, the first stage is hierarchical clustering, and then merge the clusters obtained by hierarchical clustering by cluster merging algorithm. This method improved the efficiency of large-scale text clustering. On the other hand, it can cluster increasing data in real time without the need of re-clustering th e whole data sets. 3. Cluster Merging Algorithm Previous studies rarely concern ed cluster mergin g method. Hierarchical clustering calculated the similarity be- tween two clusters by single-link, full-links or average-link. Liu Zhangxiong [9] divided data on a grid, and merged clusters on the b asis of grid characteristics. These methods are essentially based on dis tance, but they measure distance only by a single point or representative point when comparing clusters, without con s idering the overall information of clusters, which will lead to two dissimilar clusters merging. Keep i n g iterating like thi s will ultimately reduce the accuracy of cluster merging. We recon sidere d cluster merging algorithm from the p erspective of inf ormation theory, mainly based on the following basic knowledge : if two clus ters are of high similarity, after one cluster merging into the other one, the information entropy of the latter will not increase by a large margin. Corollary 1: Let B and C are two clusters to merge, and is a specific constant. If , B an d C are of a high similarity, and they can be merged. If , B and C are of a low simi- larity, and they cannot be merged. 3.1. Calculating Information Entropy of C lusters In ID3 algorithm [10], ther e ar e decision attributes in training data sets, which can be used as classification label to get the information entropy. The paper extracted important words from each cluster as classification attributes to calculate the information entropy of each cluster. Symbolic description: B = {S1, S2,..., Sm}, a clus ter sets contained m short texts; WB = {W1, W2, ... , Wp}, re- sult sets of short text segmentation of cluster B; In , |Wordi| is the number of sen- tences with “‘Wordi” in cluster B, and idfwordi can be calculated on corpus; C = {S1, S2, ..., Sn}, a short text cluster set to merge; WC = {W1, W2, ... , Wq} is similar with WB. Information Entropy Algorithm of Clusters H(B): Input: B, WB and mutual information threshold α Output: H(B) Begin (1) Choose the two maximum values of Wi in WB as word1 and word2. (2) Calculate the mutual information of word1 and word2 in short text sets, an d proceed 0 - 1 standardization for them, as Formula (1). N CB NA WordWordMI 2 2 21 log log ),( × × = (1) In Formula (1), A is the number of short texts which contained word1 and word2 simultaneously. N is the total number of sentences in short texts. B is the number of short texts contained word1, and C is the number of short texts contained word 2. (3) Divide equivalence classes on B by property P as B/P = {Join, First, Second, Noappear}. Join represents the sentence sets that contained word1 and word2 simultaneously; First repr esents the sentence sets that only contained word1 and second r epresents th e sentence sets th at only contained word 2. Noappear is th e sentence sets contained none of them. (4) Merge Join, First and Second if MI(Word1,Word2) > α, that is B/P = {marge, noappear}. Otherwise, keep unchanged. (5) Calculate th e information entropy of B as Formula (2). ∑×−= ∈PBc m c m c BH /2 || log || )( (2)  Y. Wang et al. End 3.2. Algorithm Design The above algorithm calculated the correlation between two words by mutual information, and then d ecided whether to merge the two words to divide equivalence classes. This k ind of algorithmic idea can be also applied to calculating the information entropy of merging result of two clusters. When a cluster contained few short texts merge into a cluster contained more short texts, regardless of whether they are similar, the information entropy will not chan g e a lot. Th erefore, we only need to enlarge one cluster in proportion when calculating information entropy of merging results of two clusters. Cluster merging algor ith m is as Figure 2. 3.3. Algorithm Analysis Let the total number of short texts is N, and set the size of window is m. So the number of times of hierarchical clustering is ⌈ ⌉, and each time the results of hierarchical clustering need to be merged into the base clusters formed previously. Firs t, carry out h ierar chical clustering on short texts in the window, an d the time complexity is O(m3). Set hierarchical clustering forms k c lu ster s , an d all the k clusters need to be merged into the base clus- ters formed previou sly in t urn. The number of short texts in the base class s ets w ill increase with th e number of times of merging. Complexity of the i-th merging is k*i*m. Th er e fore, time complexity of every h ierarchical clustering and merging is O(m3)+ k*i*m, then t here will be th e formula (3) after N/m times iteration : ∑ = ××+× m N i mik mO m N 1 3 )( (3) In order to expres s easily, ignore the subtle influence of rounding. Adjusting formula (3), we can get the for- mula . Regarding k and m as co nstan t, the u lti mate ti me c o mplexity is O(N2), and the same is the case with CURE clustering algorithm. In particular, the size of the sliding w indow is at tens of thousands level, so the constant coefficient of N2 is much smaller than 1. 4. Experiment and Analysis 4.1. Experiment Setups All the experiments were set up on a server, who is of Intel Xeon CPU E5-2620@2.00GHz, 8 cores, 13G mem- Figure 2. Cluster Merging Algorithm. 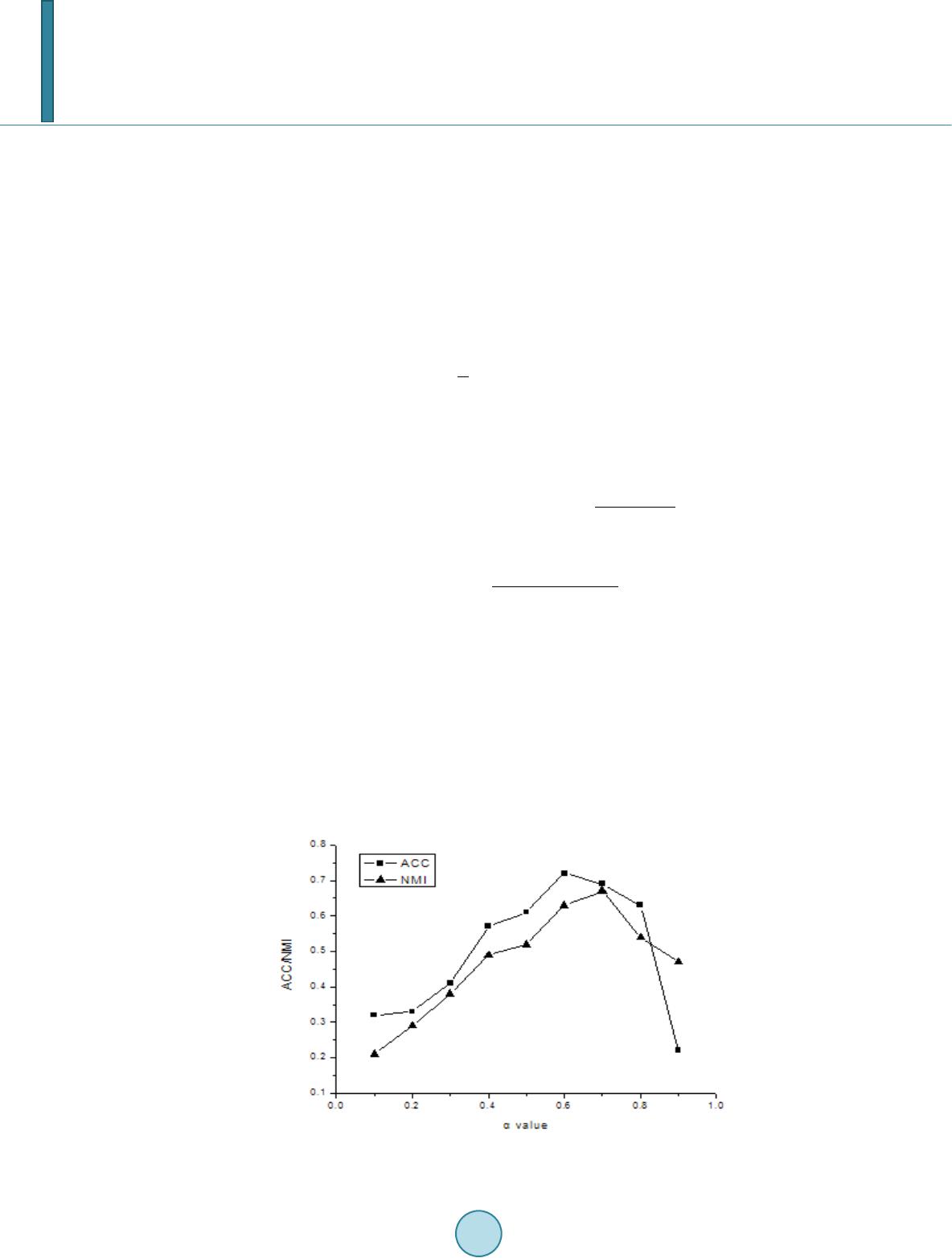 Y. Wang et al. ory and Linu x operating system. Algorith ms were written in Java and programs were single-threaded. In order to prove the effectiveness and efficiency of our algorithms, we took the traditional CURE algorithm [11] as a ref- erence. All the data in this paper come fro m an infant education company, containing a total of 103,048 short texts on the issue of babies. 10,000 of them have been classified by experts and the infant education company. There are two interrelated evaluation criteria when analyzing clu stering r esults: (1 ) the closer in a clu s ter th e better , th e more discrete between clusters the better; (2) the closer between clustering results and manual estimations the better [7]. In this paper, we used accuracy and standar d mutual information two evaluation criterions to assess clustering result s [12]. Let l(ci) as the cluster label of cluster ci, l(dj) as the manual marking category of the j-th short text, and the formula to definite the accuracy is as follows . ∑ ∑ = = = k i n jji dlcl n ACC 1 1 ))(),(( 1 δ (4) and . Set C and C’ are clu sters , an d d efin ite mutual information MI(C,C’) as Formula (5). ∑ ∈∈ = '', 2 )'()( )',( log)',()',( CcCc ji ji ji ji cpcp ccp ccpCCMI (5) Standard mutual information is as Formula (6) ))'(),(max( )',( )',( CHCH CCMI CCNMI = (6) Experiment analysis can be divided into thr ee parts . First, set different mutual information thresholds and merging thresholds, examine the accuracy and changes on standard mutual information, and determine the op- timal mutual information threshold and merging threshold. Second, compare cluster ing r esults and time com- plexity with CURE algorithm. 4.2. Parameter Determination In cluster merging algorith m, it is also n ecessary to d etermine tw o p arameters, mutual information threshold α and cluster merging threshold. When measuring α separately, set β as 0.4 by estimating samples, then tested α from 0.1 to 0.9 to determine α. After that, the parameters β was determined. But it was so onerous to analyze 10000 short tex ts th at we extracted 2500 d ata from them, and the results are show n in Figure 3 and Figure 4. Figure 3. The ACC & NMI under the changing α. 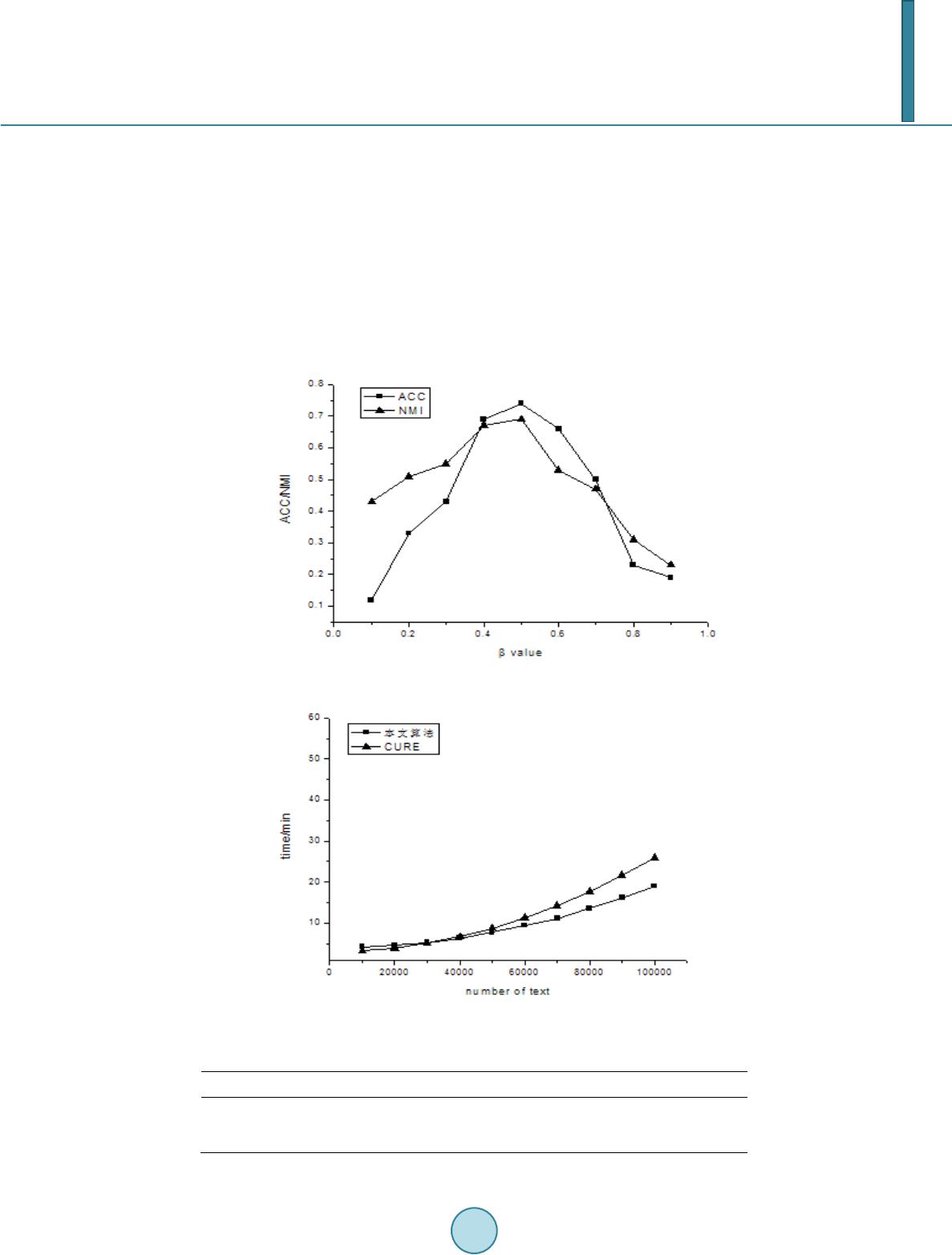 Y. Wang et al. In Figure 3 and Figure 4, standard mutual information and accuracy have similar change trend. They in- crease first, then run down after reaching the peak. When the mutual information threshold value α is small, the possibility that mutual information of two words selected from clusters is larger than α increase, which reduce the number of categories obtained by dividing the short texts taking the two words as attributes, and the entropy calculated is generally small, and then unsimilar clusters will merge, forming some big cluster sets. Similarly, the value of β will also lead to occurrence of the above situations. According to experiments, we finally deter- mined α = 0.7 and β = 0.5. 4.3. Clustering Effect Analysis For the 10000 data, we marked artificially 133 categories, including 7238 short texts. The other 2762 sentences were isolated points or indeterminate, which were not included in the categories. Now the cluster in which the Figure 4. The ACC & NMI under the changing β. Figure 5. Time performance comparison. Table 1. Clustering effect comparison between our algorithm and CURE algorithm Clusters Big categories/texts Small categories/texts ACC NMI Our algorithm 2275 161/5764 2114/4236 74.3% 69.1% 2083 143/6108 1940/3892 72.1% 63.1%  Y. Wang et al. number of texts is greater than or equal to 5 is called big category. The experiment re sults are shown in Table 1. As can be seen from the data, numbers of big categories of two algorithms are bo th larger than th e 133 categories marked artificially, and tex t algor ith m is especially lar ge. By observ ing th e clustering results, we can find that some clusters are similar in the cluster sets obtained by text algorithm, but there are also some noise data in cluster sets, and cluster do not merge. So we speculate that if the result of hierarch i cal clusterin g is not good, there will be noise data in cluster sets, a nd th en this algorithm will not merge them but make them separate clus- ters. That is to say, in par t , we have discreteness among clusters exchang e for compactness within cluster, which make noise convergence in iteration. So our algorithm is slightly higher than CURE in ACC and NMI. In addi- tion, they both do well when dealing with isolated po in ts an d abnormal points. Finally, we tested the ir performance in time from the 103048 short texts. Time chang e is sho w n in Figure 5. From Figure 5, we can see that the two algorithms are of polynomial time complexity. In addition, our algo- rithm has a lower growth rate. 5. Conclusion This paper studies volume short texts clustering problems produced by mobile Internet. We propose a two-stage clustering strategy using sliding windows according to characteristics of short texts of volume data and dynamic growth, whose time complexity is O(N2). We did hierarchical clustering in sliding window, and merged hierar- chical clustering results using information gain theory. The experiment results show that this method has consi- der ed the global feature of clusters when clustering, so it is of high accuracy. It can be easily extended to mul- ti-threaded and distributed algorith m, whic h has a good application prosp ect in la rge-scale short texts clustering. References [1] He, H., Chen, B., Xu, W., et al. (2007) Short Text Feature Extraction and Clustering for Web Topic Mining. IEEE Third International Conference on Semantics, Knowledge and Grid, 382-385. [2] Hartigan, J.A. and Wong, M.A. (1979) Algorithm AS 136: A k-Means Clustering Algorithm. Journal of the Royal Sta- tistical Society, Series C (Applied Statistics), 28, 100-108. [3] Szekely, G.J. and Rizzo, M.L. (2005) Hierarchical Clustering via Joint between-within Distances: Extending W ard’s Minimum Variance Method. Journal of Classification, 22, 151-183. http://dx.doi.org/10.1007/s00357-005-0012-9 [4] Zhao, P. and Cai, Q.S. (2007) Research of Novel Chinese Text Clustering Algorithm Based on HowNet. Computer Engineering and Applications, 43, 162-163. [5] Tang, J., Wang, X., Gao, H., et al. (2012) Enriching Short Text Representation in Microblog for Clustering. Front iers of Computer Science, 6, 88-101. [6] Wang, L., Jia, Y., Han, W. (2007) Instant Message Clustering Based on Extended Vector Space Model. Advances in Computation and Intelligence, Springer Berlin Heidelberg, 435-443. http://dx.doi.org/10.1007/978-3-540-74581-5_48 [7] Peng, Z.Y., Yu, X.M., Xu H.B., et al. (2011) Incomplete Clustering for Large Scale Short Texts. Journal of Chinese Information, 25, 54-59. [8] Chen, J.C., Hu, G.W., Yang , Z.H., et al. (2011) Text Clustering Based on Global Center-Determination. Computer En- gineering and Applications, 47, 147-150. [9] Liu, Z.X., Liu, Y.B. and Luo, L.M. (2010) An Efficient Density and Grid Based Clustering Algorithm. Journal of Chongqing University of Post s and Telecommunications (Natural Scie nce Edition), 22, 242-247. [10] Quinlan, J.R. (1979) Discovering Rules by Induction from Large Collections of Examples. Expert Systems in the Mi- cro Electronic Age. Edinburgh University Press. [11] Guha, S., Rastogi, R. and Shim, K. (1998) CURE: An Efficient Clustering Algorithm for Large Databases. ACM SIGMOD Record, ACM, 2 7, 73-84. [12] Zhou, Z.T. (2005) Quality Evaluation of Text Clustering Results and Investigation on Text Representation. Graduate University of Chinese Academy of Sciences, Beijing.
|