 Open Journal of Social Sciences, 2014, 2, 161-166 Published Online September 2014 in SciRes. http://www.scirp.org/journal/jss http://dx.doi.org/10.4236/jss.2014.29028 How to cite this paper: Wang, X.J. (2014) An Integrated Fuzzy Approach for the Evaluation of Supply Chain Risk Mitigation Strategies. Open Journal of Social Sciences, 2, 161-166. http://dx.doi.org/10.4236/jss.2014.29028 An Integrated Fuzzy Approach for the Evaluation of Supply Chain Risk Mitigation Strategies Xiaojun Wang School of Economics, Finance and Management, University of Bristol, Bristol, UK Email: xiaojun.wang@b ristol.ac.uk Received June 2014 Abstract Competing in an increasingly uncertain business environment, organizations need to mitigate its supply chain risks to enhance their resiliency. However, it is important to implement appropriate strategies to meet business needs. This paper presents a novel approach that integrates fuzzy risk assessment and fuzzy Delphi for the evaluation of strategies in order to mitigate supply chain risks. The novelty of the model lies in the fact that an analytical tool enables the specific business prefe- rences concerning supply chain risks to be taken into consideration in making the strategic deci- sions. It provides a practical solution by which companies can systematically assess the risks in- volved in the supply chain and select appropriate strategies to address them. Keywords Supply Chain Risk, Strategy Evaluation, Fuzzy Risk Assessment, Delphi 1. Introduction In a supply chain, uncertainty is a major factor that can influence the effectiveness of supply chain coordination. With the increasing trend of collaboration with international supply partners and extended supply networks, it also brings uncertainties that significantly threaten normal business operations of the organizations in the supply chain. Supply chain risk or vulnerability has emerged as a key challenge to supply chain management (SCM). Supply chain risk management (SCRM) is a field of escalating importance and is aimed at developing ap- proaches to the identification, assessment, analysis and treatment of areas of vulnerability and risk in supply chains [1]. When assessing supply chain risk, the causes, probability, and consequences for each potential risk have to be collected and documented. There has emerged a growing body of research into risk from a number of different perspectives such as economics, finance and international management [2]. In order to adapt quickly and effectively to the changing environment, supply chains need to be flexible and work in a more collaborative manner. Businesses have recognized the potential competitive advantages of being resilience in a volatile market condition, agility for coping with increased environmental uncertainty, and react- ing within smaller windows of opportunity for decision-making [3]. However, implementing appropriate strate-  X. J. Wang gies is important, because any strategic investments based on poorly considered “competencies” could be detri- mental [4] [5]. For instance, flexibility in delivery quantity and due date could lead to a reduction of production cost and, at the same time, compromise service by increasing the risk of failing to meet customer demand. In fact, the decision of adopting appropriate strategies for managing supply chain risks requires a trade-off between the benefits of implementing such strategies and cost involved. More specifically, Lee [6] expressed that alignment, adaptability, and agility are the basic ingredients for managing supply chain risks. Essentially, alignment and adaptability connote long- and medium-term perspec- tives respectively, supply chain agility enables a firm to reduce the impact of short-term changes in demand or supply [7]. Faisal et al. [8] listed several enablers for supply chain risk mitigation including information sharing, supply chain agility, trust, collaborative relationships etc. Yang et al. [9] had grouped the tools and strategies for managing supply chain risk into four main themes: multi-sourcing, alternative supply sources and backup pro- duction, flexibility, and supplier selection. Organizations are facing unique challenges in managing supply chain risks. Selecting appropriate strategies for supply chain risk mitigation is a difficult task due to the complexity of decision making. This paper provides a new approach to model the decision on supply chain risk mitigation strategies using an integrated fuzzy ap- proach. With the advantage of mathematically representing vagueness and uncertainty, fuzzy risk assessment offers a more precise and accurate analysis by encountering the uncertainty in a fuzzy environment [10]. The fuzzy Delphi method is used to extract appropriate risk mitigation strategies for evaluation by incorporating ex- perts’ opinion into consideration. Through integrating abovementioned fuzzy techniques, this research provides an analytical tool that enables the specific uncertainty concerning the supply chain to be taken into consideration in making the choice of risk mitigation strategies. It would help companies to identity appropriate strategies as well as meet their specific business needs. 2. Proposed Fuzzy Approach The approach proposed in this section focuses on prioritizing alternative strategies for mitigating supply chain risks. Firstly, supply chain risk assessment matrix is proposed to identify relevant risks and conduct an initial assessment. It is followed with quantifying the level of identified risks through the use of fuzzy set theory. Fuzzy Delphi is then applied to extract relevant supply chain risk mitigation strategies for further evaluation. 2.1. Supply Chain Risk Assessment Matrix The proposed approach starts with defining the problem under study which is the evaluation of strategies for mi- tigating supply chain risk. A system analysis is required to identify all potential supply chain risks that the busi- ness could be exposed to. In each risk category, potential risks are identified and listed, and information about risks may be collected from survey, interview, best practice, brainstorming, etc. For example, risks associated with supply cost, supply quality and supply commitment can be included in the supply risk category. The quality, time, and capacity risks associated with in-bound and out-bound logistics, and in-house operations need to be identified and listed in the process risk categories. Demand risks include risks associated with demand uncer- tainty. Similarly, based on the specific supply chain environment, risks associated with intellectual property, behavioral, and political/social risk categories need to be identified. According to the Royal Society [11], “risk is the chance, in quantitative terms, of a defined hazard occurring. It therefore combines a probabilistic measure of the occurrence of the primary event(s) with a measure of the consequences of that/those event(s)”. Hence, risk reflects both the range of possible outcomes and the distribu- tion of respective probabilities for each of the outcomes. This quantitative definition could be expresses as: (1) where R is the risk associated with a hazardous event, P represents the probability (or likelihood) of the occur- rence of the hazardous event, S represents the severity or consequence of the event. This definition can also be illustrated in the supply chain risk assessment matrix shown in Figure 1. By positioning various supply chain risks on the matrix, it gives an overall view upon all risks, and makes the most important risks requiring the most attention visible. In addition, it indicates whether the risks can be mitigated by decreasing their probability or the severity of their consequences. 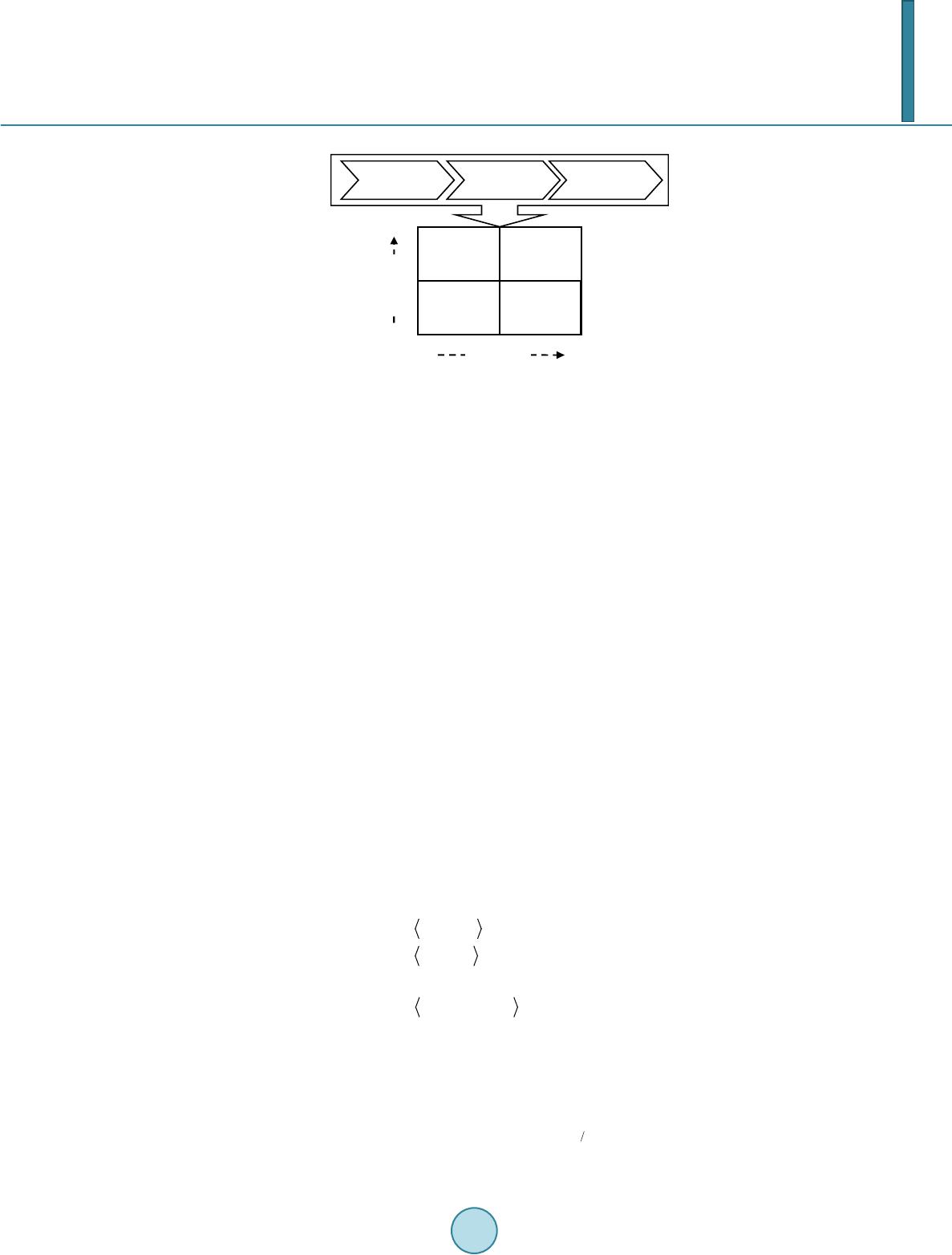 X. J. Wang Figure 1. Supply chain risk assessment matrix. 2.2. Fuzzy Risk Assessment Since there may be a number of potential risks that have been identified and managing each risk will incur cer- tain costs, it is necessary to assess the identified risks. In many cases, a full systematic and quantitative risk as- sessment along the supply chain may not be allowed due to constraints in data quality, time, or expertise. More- over, uncertainty problems cannot be expressed simply by using the concept of probability or crisp values [12]. Fuzzy set theory has been frequently used to solve problems of uncertain nature. A fuzzy number is a special fuzzy set, such that N = {(x, μN(x), x∈ F)}, where the value of x lies on the real line F→[0, 1]. TFN is employed to characterize the fuzzy values of quantitative data and linguistic terms are used in approximate reasoning. We define a fuzzy number N on F to be a triangular fuzzy number and the membership function can be described as: 12 112 33223 () / (),[,] ()() / (),[,] 0, otherwise N x nnnxnn xnxnnxnn µ − −∈ =− −∈ (2) where n1 ≤ n2 ≤ n3, n1and n3 stand for the lower and upper value of the support of N respectively, and n2 denotes to the most promising value. In practice, companies have difficulties in evaluating these factors due to uncertainty and lack of knowledge and information [13]. Instead, risk assessors often rank these risk factors in terms of linguistic variables such as high, moderate and low, etc. In this research, the qualitative scales are expressed by TFNs to capture the vague- ness in the linguistic subjectivity of risk definitions. Table 1 describes this qualitative scaling system for severi- ty of the risk, probability of an adverse effect consequential to the risk. Two fuzzy numbers Np and Ns with membership functions Np(x) and Ns(x) the grades of the two factors respectively. To determine the magnitude and intensity of the risk, the two risk factors are multiplied to produce the risk evaluation. The product of two TFNs is also a fuzzy member, but not necessary a triangle. To simplify multipli- cation calculations, a standard approximation is used. The standard approximation has been defined in the forms described as: 12 3 12 3 112233 ,, ,, ,, Aaa a Bbb b CAB Cab abab → → = ⊗ → (3 ) To ensure accuracy of the assessment, group risk assessment is incorporated in the model. First of all, a risk assessment team or group is formed. With reference to Table 1, a set of integers (from 1 to 11) are assigned to the two elements for each risk item in the supply chain risk assessment matrix by individual assessors. Using fuzzy geometric mean, both fuzzy grading for the severity and likelihood of each item can be obtained using Equation (4) and Equation (5) respectively: ( ) 1 12 n ii iin ssss=⊗⊗⊗ (4)  X. J. Wang Table 1. Linguistic classification of risk grades. Grade of risk A qualitative explanation of probability of risk (p) A qualitative explanation of severity of the consequence (s) Triangular fuzzy numbers (TFN) 1 Definitely low Definitely no effect (0.0, 0.0, 0.1) 2 Extremely low Extremely minor (0.0, 0.1, 0.2) 3 Very low Very minor (0.1, 0.2, 0.3) 4 Low Minor (0.2, 0.3, 0.4) 5 Slightly low Slightly minor (0.3, 0.4, 0.5) 6 Middle Middle (0.4, 0.5, 0.6) 7 Slightly high Slightly severe (0.5, 0.6, 0.7) 8 High Severe (0.6, 0.7, 0.8) 9 Very high Very severe (0.7, 0.8, 0.9) 10 Extremely high Extremely severe (0.8, 0.9, 1.0) ( ) 1 12 n ii iin pppp =⊗ ⊗⊗ (5 ) With the fuzzy grading, the risk level of identified risk item can be calculated individually as: () , , iii i ii gsp LgMgUg = ⊗ = (6) where represent the lower, middle and upper values of the fuzzy grade of the ith risk item. Since the calculation so far involves fuzzy variables, the next step is to defuzzify the grades to form meaningful fig- ures for analysis (e.g. ranking). Many methods exist in the literature but Centre of Area (COA) is by far the most popular and easy to use one. Then, using the COA method, the non-fuzzy risk value of the ith risk item is given as: () () 3 i ii iii gUg LgMg LgLg =−+ −+ (7) The higher value indicates a higher risk level of the assessed risk item. 2.3. Risk Mitigation Strategy Evaluation with Fuzzy Delphi Many strategies that mitigate supply chain risks have been discussed in the literature. While it is good to have choices of strategies for mitigating supply chain risks, how to tailor them with their various features and benefits is still a big challenge. Here, fuzzy Delphi is applied to select relevant risk mitigation strategies for further eval- uation. Following the references of [14]-[16], the steps for executing the fuzzy Delphi method are described as follow: Step 1: Conduct a questionnaire and organize an appropriate panel of expert to express their most conserva- tive (minimum) value and the most optimistic (maximum) value of the importance of each strategy in the possi- ble strategy set S in a range from 1 to 10. A score is then denoted as , where and are the conservative index and the optimistic index of strategy i rated by expert k respectively. Step 2: Organize expert opinions collected from questionnaires and determine the TFNs for the most con- servative index and the most optimistic index for each strategy i. Use the conservative index as an example, indicates the minimum of all the experts’ most conservative value as: (8 ) The is the geometric mean of all the experts’ most conservative value for strategy i. It is obtained  X. J. Wang through: (9) indicates the maximum of all the experts’ most conservative value as: (10) In the same way, the minimum (LOi), geometric mean (MOi), and the maximum (UOi) of the group’s most optimistic values for strategy i can be obtained. Step 3: Calculate the TFNs for the most conservative index Ci = (LCik, MCik, UCik) and the most optimistic index Oi = (LOik, MOik, UOik) for the remaining strategies, . Step 4: Examine the consistency of experts’ opinions and calculate the consensus significance value, Gi for each strategy. The gray zone ([15] [17]), the overlap section of Ci and Oi in Figu re 2, is used to examine the consensus of experts in each strategy and calculate its consensus significance value, Gi,. If the TFN pair does not overlap (i.e. ) and no gray zone exists, the expert options in strategy i achieve consensus, the consensus significance value is calculated as: (11) If there is an overlap (i.e. UCi > LOi) and the gray zone interval value gi is equal to , and gi is less than the interval value of Ci and Oi , that is, gi < di, then the consensus significance value G is determined in accordance with cross point of gray zone in Figure 2. The consensus significance value Gi of each strategy can be calculated by Equation (12) and (13). ( ) ( ) ( ) { } max min, iLU P Gpp dp µµ = ∫ (12) () () i ii i ii iii UC MOLO MC GUCMCMOLO × −× =−+− (13 ) If the gray zone exists and gi < di, then there are great discrepancies among the experts’ opinions. Repeat steps 1 to 4 until a convergence is attained. Adapted from (Ishikawa et al. [18]) Step 5: Extract strategies from the candidate list. Compare consensus significance value with a threshold val- ue, T, which is determined by experts subjectively based on the geometric mean of all consensus significance value Gi [15] [17] [18]. If Gi > T, strategy i is then selected for further evaluation. 3. Conclusion This paper presents a novel approach that enables to perform structured analysis of supply chain risks and eva- luate different strategies for mitigating these risks. The novelty of the model lies in the fact that an analytical tool enables the specific business preferences concerning supply chain risks to be taken into consideration in making the strategic decisions. It is a systematic method which is capable of capturing a human’s appraisal of ambiguity when complex multi-criteria decision making problems are considered. It offers a more precise and Figure 2. Gray zone of Ci and Oi.  X. J. Wang accurate analysis by incorporating the uncertainty that is encountered in a fuzzy environment. It is considered to be supportive for managers in planning and making significant strategic decisions on supply chain risk man- agement. Nevertheless, the presented approach also has its own limitations, which imply fruitful directions for future research. For instance, users have to make subjective decisions when conducting fuzzy risk assessment and ob- tain priority ratings for alternative strategies. In fact the functionality of the model is highly dependent on the knowledge, expertise and communication skills of the decision makers. Therefore, one future research is to con- sider a more objective assessment technique such as entropy method. Moreover, there may be some mutual in- teractions between assessment items, which may have consequent effect on the level of supply chain risk. Another possible future research direction would be to use the network approach to incorporate inner and outer dependencies that occur between identified risk items. References [1] Neiger, D., Botaru, K. and Churilov, L. (2009) Supply Chain Risk Identification with Va lue -Focused Process Engi- neering. Journal of Operations Management, 27, 154-168. http://dx.doi.org/10.1016/j.jom.2007.11.003 [2] Jüttner, U., Peck, H. and Christopher, M. (2003) Supply Chain Risk Management, Outlining an Agenda for Future Re- search. International Journal of Logistics, 6(4), 197-219. http://dx.doi.org/10.1080/13675560310001627016 [3] Giachetti, R.E., Martinez, L.D., Saenz, O.A. and Chen, C.S. (2003) Analysis of the Structural Measures of Flexibility and Agility Using a Measurement Theoretical Framework. International Journal of Production Economics, 86, 47-62. http://dx.doi.org/10.1016/S0925-5273(03)00004-5 [4] Narasimhan, R., Talluri, S. and Das, A. (2004) Exploring Flexibility and Execution Competencies of Manufacturing Firms. Journal of Operations Management, 22, 91-106. http://dx.doi.org/10.1016/j.jom.2003.12.003 [5] Sawhney, R. (2006) Interplay between Uncertainty and Flexibility across the Val ue -Chain: Towards a Transformation Model of Manufacturing Flexibility. Journal of Operations Management, 24, 476-493. http://dx.doi.org/10.1016/j.jom.2005.11.008 [6] Lee, H. (2004) The Triple—A Supply Chain. Harvard Business Review, 102-112. [7] Tang, C. and Tomlin, B. (2008) The Power of Flexibility for Mitigating Supply Chain Risks. International Journal of production Economics, 116, 12-27. http://dx.doi.org/10.1016/j.ijpe.2008.07.008 [8] Faisal, M.N., Banwet, D.K. and Shankar, R. (2006) Supply Chain Risk Mitigation: Modeling the Enablers. Business Process Management Journal, 12, 535-552. http://dx.doi.org/10.1108/14637150610678113 [9] Yang, Z.B., Aydin, G., Babich, V. and Beil, D.R. (2009) Supply Disruptions, Asymmetric Information, and a Backup Production Option. Management Science, 55, 192-209. http://dx.doi.org/10.1287/mnsc.1080.0943 [10] Chan, H.K. and Wang, X. (2013) Fuzzy Hierarchical Model for Risk Assessment: Principles, Concepts, and Practical Applications. Springer, London. http://dx.doi.org/10.1007/978-1-4471-5043-5 [11] The Royal Society (1992), Analysis, Perception and Management, The Royal Society, London. [12] Wang, X., Li, D. and Shi, X. (2012) A fuzzy Enabled Model for Aggregative Food Safety Risk Assessment in Food Supply Chains. Production Planning and Control, 23, 377-395. http://dx.doi.org/10.1080/09537287.2011.561812 [13] Wang, X., Chan, H.K., Yee, W.Y. and Diaz-Rainey, I. (2012) A Two-Stage Fuzzy-AHP Model for Risk Assessment of Implementing Green Initiatives in the Fashion supply Chain. International Journal of Production Economics, 135, 595-606. http://dx.doi.org/10.1016/j.ijpe.2011.03.021 [14] Kuo, Y.F. and Chen, P.C. (2008) Constructing Performance Appraisal Indicators for Mobility of the Service Industries Using Fuzzy Delphi Method. Expert Systems with Applications, 35, 1930-1939. http://dx.doi.org/10.1016/j.eswa.2007.08.068 [15] Lee, A.H.I., Wang, W. and Lin, T. (2010) An Evaluation Framework for Technology Transfer of New Equipment in High Technology Industry. Technological Forecasting & Social Change, 77, 135-150. http://dx.doi.org/10.1016/j.techfore.2009.06.002 [16] Wang, X. and Durugbo, C. (2013) Analysing Network Uncertainty for Industrial Product-Service Delivery: A Hybrid Fuzzy Approach. Expert Systems with Applications, 40, 4621-4636. http://dx.doi.org/10.1016/j.eswa.2013.01.062 [17] Hsiao, T.Y. (2006) Establish Standards of Standard Costing with the Application of Convergent Gray Zone Test. European Journal of Operational Research, 168, 593-611. http://dx.doi.org/10.1016/j.ejor.2004.05.012 [18] Ishikawa, A., Amagasa, T., Shiga, T., Tomizawa, G., Tatsuta, R. and Mieno, H. (1993) The Max-Min Delphi Method and Fuzzy Delphi Method via Fuzzy Integration. Fuzzy Sets Systems, 55, 241-253. http://dx.doi.org/10.1016/0165-0114(93)90251-C
|