 Energy and Power En gi neering, 2011, 3, 96-106 doi:10.4236/epe.2011.32013 Published Online May 2011 (http://www.SciRP.org/journal/epe) Copyright © 2011 SciRes. EPE Application of Ant Colony Algorithm to the Analysis of Common Mode EMI Model of DC Motor Jinfeng Liu1, Xudong Wang1, Jiang Nan2 1School of Electrical & Electronic Engineering, Harbin University of Science & Technology, Harbin, China 2Department of Electrical and Computer Engineering, Stevens Institute of Technology, Hoboken, USA E-mail: ljf78118@163.com Received December17, 2010; revised March 21, 2011; accepted March 31, 2011 Abstract The Electromagnetic Compatibility (EMC) of Direct Current (DC) motor windings is a system model which is used to reflect the functional characters of the system in the whole EMC specified frequency (150 KHz - 30 MHz). For most motor designing process, it is always used to evaluate the inductance of windings in lower or working frequency; however, when analyzing the conducted interference, it is necessary to take some parameters in high frequency into account in building up the EMC model, such as the noticeable ca- pacitance distributed among the windings or between windings and shells. Past research neglected the com- mon-mode current generated by the high frequency interference within motor bearings coupled with shells, since the parasitic capacitance of rotor core comes from armature windings supplied sufficient paths. In EMC modeling process for DC motor problem, first, test the impedance of windings by experiments; then, generate the equivalent circuit with overall parameters. At present, it is a difficulty that how to choose the parameters. Most researchers preferred to adopt analytical calculation results, however, it could not reflect the essence of the model since it requires many simplification. Based on this point, this paper adopted Ant Colony Algorithm (ACA) with positive feedback to intelligently search and globally optimize the parameters of equivalent circuit. Simulation result showed that the impedance of equivalent circuit calculated by this algorithm was the same as experimental result in the whole EMC frequency. In order to further confirm the validity of ACA, PSPICE circuit simulation was implemented to simulate the spectrum of common mode Electromagnetic Interference (EMI) of equivalent circuit. The simulation result accords well with the ex- periment result received by EMI receiver. So it sufficiently demonstrated correctness of ACA in the analysis of high frequency equivalent circuit. Keywords: Common Mode EMI, Motor Windings, Ant Colony Algorithm, PSPICE Simulation, EMI Receiver 1. Introduction As the development of communication technology, computer science, automatic control, vehicles, household appliance, electric power industry and military, the re- quirement of DC motors increased significantly. Since it is the key component in the domains mentioned above, the types and quantity of DC motors improved rapidly. At the same time, the structure and control of DC motors has changed significantly. However, as the key compo- nent of many systems (such as electrical vehicles and forklifts), the DC motors have become the serious inner interference source of these systems, since when it oper- ates, during the steering process and the unstable touch between brush and commutator, there will generate tran- sient voltage on the wires. These transient voltages will invade into other components as conducted interference through conductors [1]. As a result, it is essential to build up a correct high frequency model of DC motors in order to improve the electromagnetic compatibility of the sys- tem. Jens Benecke from German built high frequency The Key Science-Technology Project of Heilongjiang Province (GB08A306). Youth Foundation of Harbin University of Science & Technology.  J. F. LIU ET AL. 97 model of permanent magnet direct current motor with 12V low voltage, which contains three parts [2]. It was not only complicate in modeling, but the parameters were also hard to achieve. Meanwhile, Kohji Maki from the United States utilized 3D electromagnetic field analysis to build EMC simulation model of alternating current (AC) motor [3] and French scholar C. Martis built high frequency EMI model of permanent magnet DC motor [4]. To improve precision and reduce com- plexity of model, this paper takes the separately excited DC motor produced by Liaoning Motor Maker as exam- ple to build up the EMC model. In this process, besides building up the physical model according to motor char- acters, we need to set up the parameters of each element in it. This paper adopted Ant Colony Algorithm to de- termine the parameters in model. This Algorithm is a new distributing evolution algorithm. It is strong in solu- tion searching, adaptability and robustness; it could also optimize the parameter collection process and make the impedance of equivalent circuit in model equal to meas- ured value. 2. EMC Model of Separately Excited DC Motor Windings The common-mode equivalent circuits mentioned in [5] and [3] are applied to analyze and predict the over volt- age on motor, shaft voltage/current and other negative effect generated by common-mode voltage. Even use it to analyze the common-mode circuit for leakage current, it is only effective in frequency lower than 1MHz, hard to face the requirement of EMI of whole conducted in- terference frequency (150 kH2 - 30 MHz). The main dif- ference between the high frequency common-mode equivalent circuit of separately excited DC motors and that of former ones is this model could be used to ana- lyze and measure the emission intensity of common- mode EMI and motor side common-mode EMI current in the whole conducted interference frequency. 2.1. The Common Mode Current Coupled Path of Separately Excited DC Motor The excitation and armature windings in the slots of sta- tor and rotor inside separately excited DC motor are symmetrically distributed along the circle. That makes the DC motor have plenty of electromagnetic coupled inside and applied sufficient path for high frequency EMI noise while there are electromagnetic and electrical field inside the motor. Though there are many parasitic parameters in motors, considered the separated power supplement for excitation and windings, while the speed control of motor is achieved by PWM controller on windings, the armature windings is the main component of the system to generate high frequency common mode EMI. Accordingly, the parasitic capacity is mainly achieved by measuring the armature windings. There are mainly 3 types of parasitic capacity, the capacity from armature windings to rotor core (Csa), the capacity from armature windings to stator core (Csf), and the capacity from excitation windings to stator core (Csg) [6]. According to the distribution of parasitic parameters of separately excited DC motor, the common mode current coupling path is showed in Figure 1, where Za and Zf represents the resistance of unit length of armature and excitation windings, respectively; Rb is the resistance of Figure 1. Common mode current couple d path inside separately excited DC motor. Copyright © 2011 SciRes. EPE  J. F. LIU ET AL. Copyright © 2011 SciRes. EPE 98 bearing, Pa and Na, Pf and Nf is the positive and negative node of power supplement to armature and excitation windings, respectively, while the supplement to armature windings is achieved through the power converter; icm is large input common mode current, iacmk, ifcmk, igcmk (while k = 1, 2,, n) is the common mode current of related parasitic capacity flows each length unit. Based on the analysis of the distribution of parasitic capacity inside the motor showed in Figure 1 and motor structure, armature winding is seriously affected by high frequency interference, while excitation windings are less affected when working under high quality power supplement. Therefore, we can neglect the effect of ex- citation windings to common mode current and only take parasitic capacity into account when analyzing the com- mon mode current path. 2.2. EMC Model Foundation of Separately Excited DC Motor The most effective method in discovering high frequency characters of motor windings is multi-conductor and multi-element conducting model. For specified DC mo- tor, armature core is the homogeneous media in all direc- tions and each rotor slot shares the same structure, the path which winding turns and wire diameter is specified, respectively; as a result, motor windings could be con- sidered as a uniform conductor. In analyzing and meas- uring the high frequency common-mode motor side cur- rent of DC motors, we could adopt lumped parameter model since it is simplified. This paper built up the EMC model of DC motor windings based on the analysis of separately excited DC motor accorded to former work, which is showed in Figure 2. In Figure 2, where La is the common-mode inductance and Ca is parasitic capacity of armature windings; R a is the sum of eddy current effect of core and resistance of Figure 2. High frequency common mode equivalent circuit of separately excited DC motor. armature windings; Lr is impedance of armature core; Cr is the sum of parasitic capacity between armature wind- ings and rotor slot and parasitic capacity among armature core laminations; Rr is the sum of resistance of armature laminations and resistance of motor bearing; Cf is the parasitic capacity of armature windings coupled to exci- tation windings core. After had this equivalent circuit, we move on to calculate each parameter above according to given characters of motor. Here we use Ant Colony Algorithm. For the equivalent circuit showed in Figure 2, ac- corded to circuit theory, it is easy to get the expression of resistance of windings ZXY and the common-mode resis- tance to earth ZXG as following: 2 1 aa XY aa aa RsL Zs RCs LCs (1) 2 2 23 1 1 aa XG aa aa rr rr rfrrf rrf RsL Zs RCs LCs RCs LCs CCsRCC sLCC s (2) 3. Ant Colony Algorithm Ant Colony Algorithm, ACA, is a new evolution simu- lated algorithm. It searches the optimized solution through the evolution process of the group combined by candidate solution. This algorithm adopts positive feed- back mechanism in order to implement intelligent searching and global optimization; meanwhile, it has strong robustness [7]. 3.1. Principle of ACA Suppose there are m parameters to optimize, denoted as p1, p2, pm, for any one among them pi (1 ≤ i ≤ m), set it as N possible non-zero value, combined set Qpi. Then, all the ants leave the formicary for food, and each ant starts from set Qpi based on the pheromone j(Qpi) of each ele- ment in set and state transition probability k jP PQ i, randomly choose one and only one element in set Qpi independently. State transition probability and phero- mone are calculated by (3) and (4), respectively. 1 i ji k jP N gi g P P PQ Q Q (3) ii PPjj QtnQt Q i Pj (4) where ρ is the duration indice of residue information and 1-ρ is the volatility; i PjQ is the increased phero-  J. F. LIU ET AL. 99 mone on j th element caused by all the ants in this loop. This increase is determined by the difference of analyti- cal and concrete output, the smaller the difference be, the more the pheromone increases [8]. After all ants finished choosing elements in the set, they get the food source. Then adjust the pheromone of each element. This process will be repeated until the op- timized solution would be found or reach the iteration times [9]. 3.2. Parameter Selection Based on ACA The mechanism of ACA path searching shows that there is essential effect from parameter selection to the per- formance of ACA. However, there is no theory support for parameter setting. Thus we need to get the optimized solution by experience through repeated matching and adjustment [10]. The scale of solution space N and num- ber of ants K are close related to the efficient of opti- mized solution searching, accuracy and global superior- ity of solution, and other optimization function. If the optimized solution is dense in parts, it is better to choose large N. The selection of K is related to N, the larger N is, the lager K is required, meanwhile, it should take the time complexity of the algorithm into account in the se- lection of K [11]. Normally, the duration indices of resi- due information is 0.5 ≤ ≤ 1 and 0.7 is optimized; total pheromone value Q is 1 ≤ Q ≤ 10 000 and has little effect to algorithm. Since the selection range of Q is much lar- ger than that of , in practical, we set randomly first, than calculate the value of Q; after get a value of Q, re- adjust in order to get a more optimized solution. Re- peat this process by times, the optimized parameter group would be finally reached [12]. 3.3. Implementation of ACA in EMC Modeling of DC Motor The common-mode current equivalent circuit of sepa- rately excited DC motor shows that there are 7 parame- ters need to set by ACA. According to the characters of motor, set up the candidate solution group (7 × 30), that is the set Qpi required by ACA, where m = 7, N = 30. Figure 3 shows the flowchart of setting the parameter in equivalent circuit using ACA. Based on experience and experiment result, we have following conclusion about ACA parameter selection: maximized number of loops NcMAX = 1000, duration indices of residue information ρ = 0.7, total pheromone Q = 700, number of ants M = 150, deviation E is limited to 0.1 (the smallest error allowed by algorithm). At the beginning, the original pheromone of each element in the set (1 ≤ j ≤ N) and , put all the ants into the formicary. Each ant choose the solution space according to state transition probability, and then take the parameter each ant chose into the H function and get the vector coefficient. After that, use freqs() function to calculate the amplitude and frequency output response of simulated filter constructed by these vector coeffi- cients, the frequency bandwidth of this function is 150 kHz - 30 MHz. The pheromone of each ant will be ad- justed by the difference of analytical output and simulate output. After all the ants reached food sources, record the deviation of optimized solution; if the deviation faces the requirement, stops calculating, or continue. If all 150 ants after 1000 loops of searching could not reach the requirement, we should reconsider whether ACA is suit- able for this type of problems. 3 i PjQt 0 i PjQ 4. Experiment and Simulation 4.1. Experiment Analysis In order to get the high frequency EMI model of motor, it is necessary to achieve the amplitude and frequency characters of resistance of motor through experiment. Then equal it into a lumped-parameter circuit to make the analytical impedance of equivalent circuits the same as tested impedance of windings. We adopted Agilent 4249A precision impedance analyzer produced by Agilent Technology to test the impedance of motor. Its scale range is from 40 Hz to 110 MHz, covered the fre- quency bandwidth talked in this paper. Use that analyzer to test the short and open circuit impedance of XQ-7A2 separately excited DC motor. The testing principle showed in Figure 4(a) and (b). Figure 5(a) and (b) showed the test result of ampli- tude and frequency characters of short and open circuit impedance when DC motor operates in 150 kHz - 30 MHz frequency bandwidth. From the figure we found it is necessary to take the parasitic parameters related with common-mode signals inside the motors into account when setting up the high frequency common-mode equivalent circuit of separately excited DC motor. 4.2. Analysis of High Frequency Model of DC Motor In order to achieve the parameters of equivalent circuit, we adopted ACA to optimize the selection of parameter group. The training curve showed in Figure 6. After 200 times of training, the result reached the accuracy re- quirement. The parameters of output equivalent circuit showed in Table 1. Comparison of simulate and test result of short and Copyright © 2011 SciRes. EPE 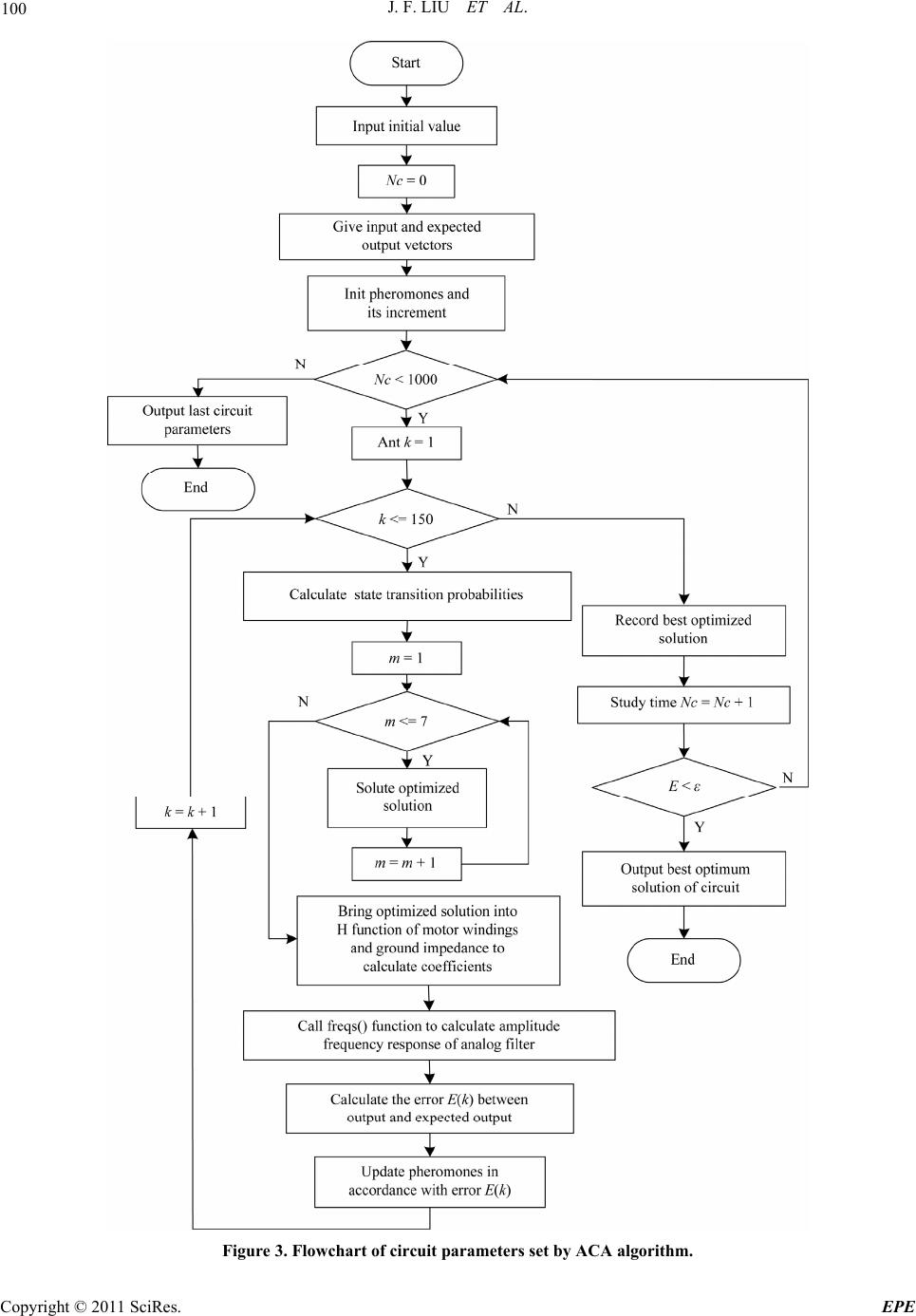 J. F. LIU ET AL. Copyright © 2011 SciRes. EPE 100 Figure 3. Flowchart of circuit parameters set by ACA algorithm. 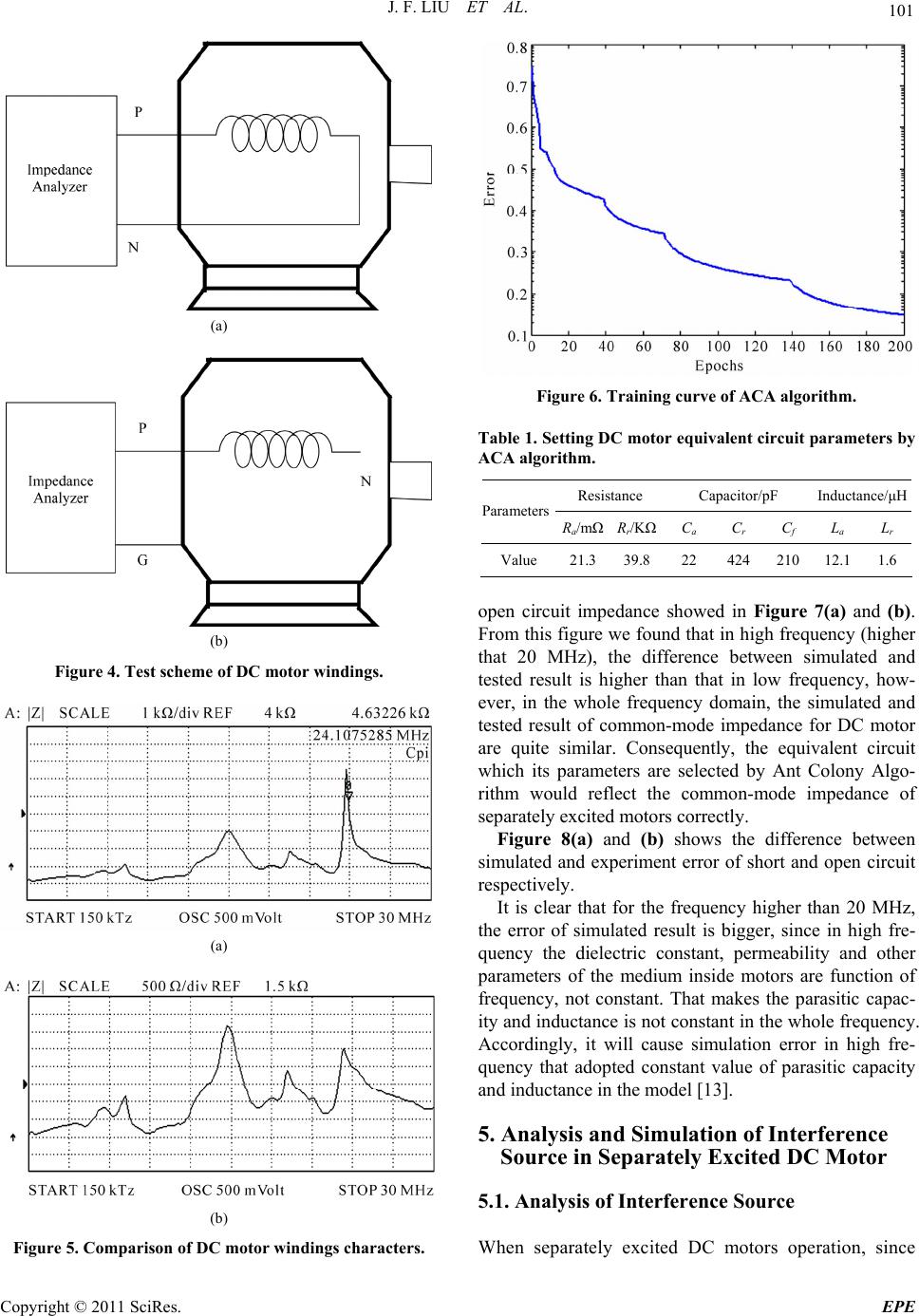 J. F. LIU ET AL. Copyright © 2011 SciRes. EPE 101 (a) (b) Figure 4. Test scheme of DC motor windings. (a) (b) Figure 5. Comparison of DC motor windings characters. Figure 6. Training curve of ACA algorithm. Table 1. Setting DC motor equivalent circuit parameters by ACA algorithm. Resistance Capacitor/pF Inductance/μH Parameters Ra/mΩRr/KΩCa C r C f L a L r Value 21.339.822 424 210 12.11.6 open circuit impedance showed in Figure 7(a) and (b). From this figure we found that in high frequency (higher that 20 MHz), the difference between simulated and tested result is higher than that in low frequency, how- ever, in the whole frequency domain, the simulated and tested result of common-mode impedance for DC motor are quite similar. Consequently, the equivalent circuit which its parameters are selected by Ant Colony Algo- rithm would reflect the common-mode impedance of separately excited motors correctly. Figure 8(a) and (b) shows the difference between simulated and experiment error of short and open circuit respectively. It is clear that for the frequency higher than 20 MHz, the error of simulated result is bigger, since in high fre- quency the dielectric constant, permeability and other parameters of the medium inside motors are function of frequency, not constant. That makes the parasitic capac- ity and inductance is not constant in the whole frequency. Accordingly, it will cause simulation error in high fre- quency that adopted constant value of parasitic capacity and inductance in the model [13]. 5. Analysis and Simulation of Interference Source in Separately Excited DC Motor 5.1. Analysis of Interference Source When separately excited DC motors operation, since 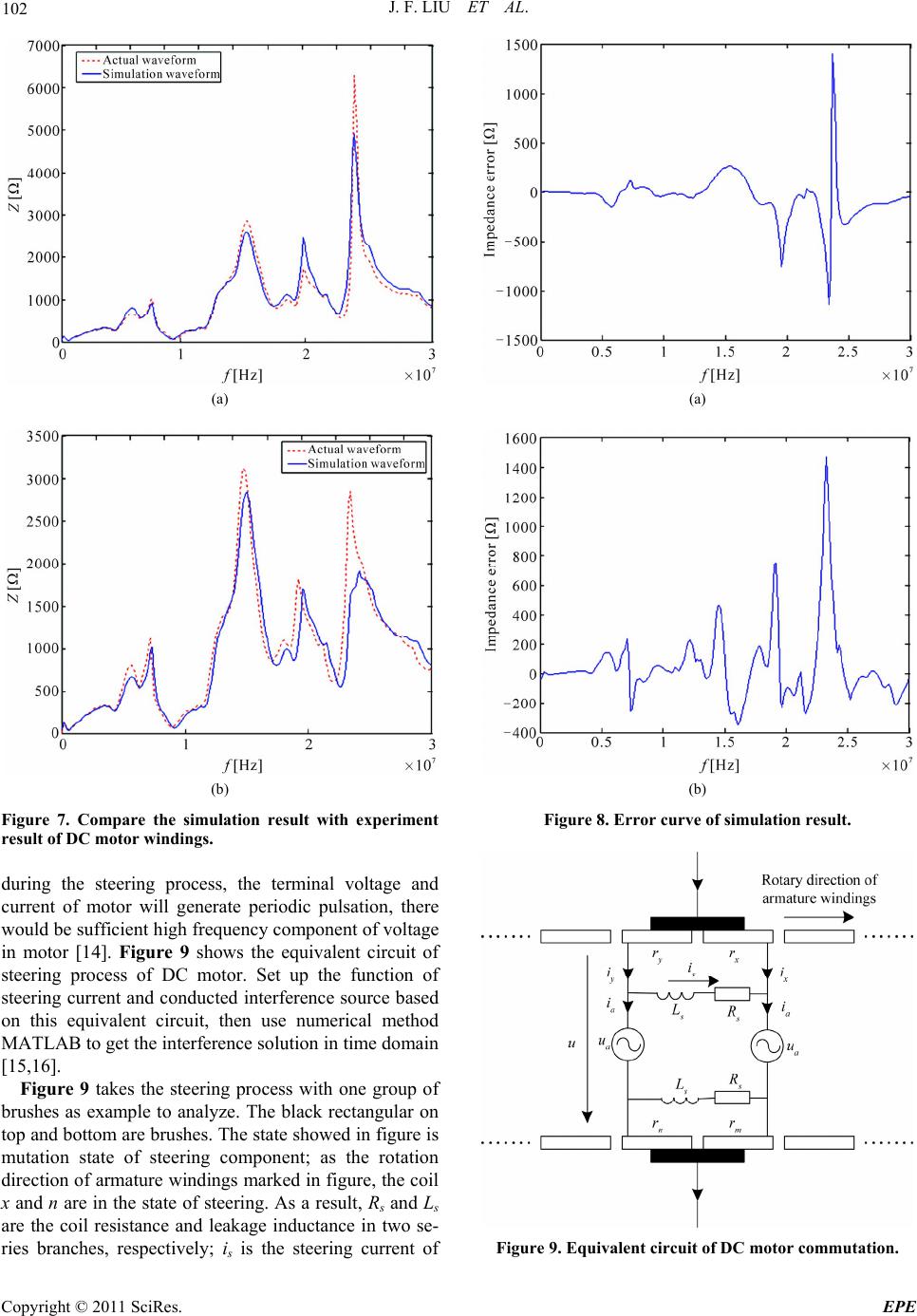 102 J. F. LIU ET AL. (a) (b) Figure 7. Compare the simulation result with experiment result of DC motor windings. during the steering process, the terminal voltage and current of motor will generate periodic pulsation, there would be sufficient high frequency component of voltage in motor [14]. Figure 9 shows the equivalent circuit of steering process of DC motor. Set up the function of steering current and conducted interference source based on this equivalent circuit, then use numerical method MATLAB to get the interference solution in time domain [15,16]. Figure 9 takes the steering process with one group of brushes as example to analyze. The black rectangular on top and bottom are brushes. The state showed in figure is mutation state of steering component; as the rotation direction of armature windings marked in figure, the coil x and n are in the state of steering. As a result, Rs and Ls are the coil resistance and leakage inductance in two se- ries branches, respectively; is is the steering current of (a) (b) Figure 8. Error curve of simulation result. Figure 9. Equivalent circuit of DC motor commutation. Copyright © 2011 SciRes. EPE  J. F. LIU ET AL. 103 mutation component, since the circuit is symmetric, it is sufficient to analyze one branch only; rx and ry are con- tact resistance between brush and two commutating segments, respectively; meanwhile, ix and iy are the cur- rent flows into commutating segments through brush, respectively. Two ua branches are the two paralleled ar- mature winding branches and ua is the back electromo- tive force of armature branch, and ia is the current in this branch. According to Kirchhoff law, the voltage function of brush circuit showed in top of Figure 9 can express as: d0 d s sssxxyy i LRiriri t (5) as iii (6) a iii s a y (7) When motor operating, the total outside voltage drop is composed by the contact voltage drop of the pair of brush uc and the back electromotive force of the branch ua, accordingly: c uu u (8) Based on electric machine theory, the back electromo- tive force of armature ua is a certain constant when the motor rotates stable. Accordingly, the effect from ua to conducted electromagnetic interference is negligible. That reveals the transient voltage when motor operating mainly comes from the contact voltage drop of brushes, especially by the end of the commuting process. The acute changes of contact voltage drop become the main resource of conducted interference in the motor. From Figure 6 we found: cxxy uriri (9) Suppose the contact between commutating segment and brushes is ideal, the contact resistance is: k xd k T rR Tt (10) k yd T rR t (11) where Rd is the contact resistance when commutator contact with brush completely, Tk is the mutation period of DC motor, expressed as: kk k k ka a bb TD vvD (12) where bk is the width of commutator. Dk and Da are the diameter of commutator and armature, respectively; vk and va are the linear velocity of the surface of commuta- tor and armature, respectively [19]. Here the rated speed of motor is 1400 rpm, then take parameter Dk = 360 mm, bk = 100 mm into Equation (12), get the rated operation steering period is around 38.4 ms. Since during the commuting process of DC motor, the transient current affects seriously to sensitive compo- nents, the effect from voltage drop is negligible and Equation (5) is changed into: d0 d s sxxyy i Lriri t (13) Take (6), (7), (10) and (11) into (13), we have the function of commuting current is in time domain: d d skk kk da ds kk iTT TT LRi ttTtTt t Ri (14) 5.2. Simulation of Interference Source Equation (14) is a typical first order differential equation and we can use solution command ode45 in MATLAB to get is in time domain. Set up the starting steering current is(0) = 10A, steering period Tk = 38.4e – 3 s, time slot t = 0.5e – 7 s, from former simulation result, we have the parameters of motor: Ls = 121 μH, Rd = 21.3 m, ia = 10A. With the help of above, we have the solution of steering current is in time domain, and the curve showed in Figure 10. From the commutating current we could see that the current changed rapidly during the steering process, and this rapid change would cause transients of contact volt- age between brush and commutator, even generate elec- tric sparks. Figure 10. Curve of commutating current. Copyright © 2011 SciRes. EPE 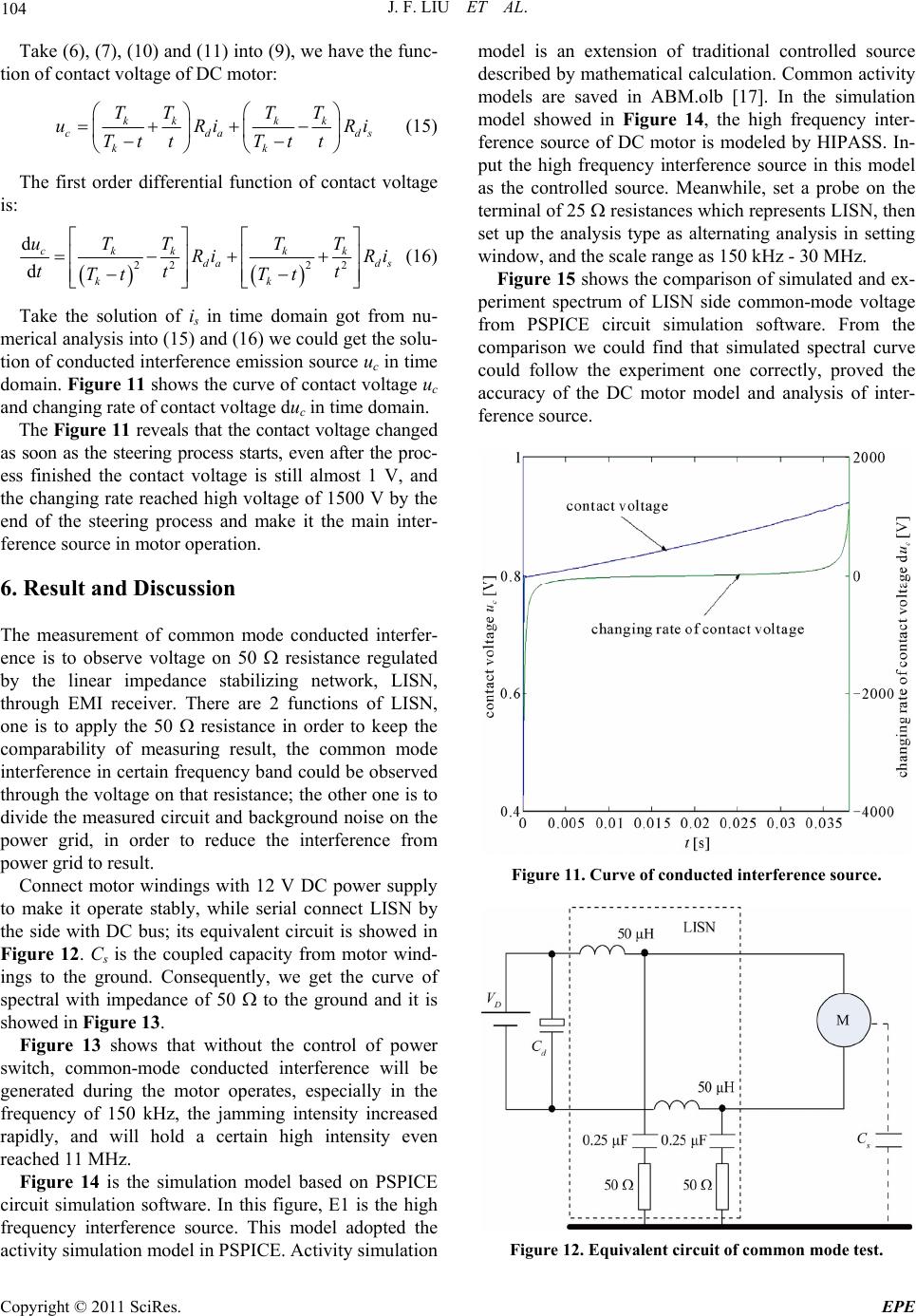 104 J. F. LIU ET AL. Take (6), (7), (10) and (11) into (9), we have the func- tion of contact voltage of DC motor: kk kk cda kk TT TT uRi Tt tTtt ds Ri (15) The first order differential function of contact voltage is: 22 22 d d ckk kk da ds kk uTT TT Ri Ri tt Tt Tt t (16) Take the solution of is in time domain got from nu- merical analysis into (15) and (16) we could get the solu- tion of conducted interference emission source uc in time domain. Figure 11 shows the curve of contact voltage uc and changing rate of contact voltage duc in time domain. The Figure 11 reveals that the contact voltage changed as soon as the steering process starts, even after the proc- ess finished the contact voltage is still almost 1 V, and the changing rate reached high voltage of 1500 V by the end of the steering process and make it the main inter- ference source in motor operation. 6. Result and Discussion The measurement of common mode conducted interfer- ence is to observe voltage on 50 resistance regulated by the linear impedance stabilizing network, LISN, through EMI receiver. There are 2 functions of LISN, one is to apply the 50 resistance in order to keep the comparability of measuring result, the common mode interference in certain frequency band could be observed through the voltage on that resistance; the other one is to divide the measured circuit and background noise on the power grid, in order to reduce the interference from power grid to result. Connect motor windings with 12 V DC power supply to make it operate stably, while serial connect LISN by the side with DC bus; its equivalent circuit is showed in Figure 12. Cs is the coupled capacity from motor wind- ings to the ground. Consequently, we get the curve of spectral with impedance of 50 to the ground and it is showed in Figure 13. Figure 13 shows that without the control of power switch, common-mode conducted interference will be generated during the motor operates, especially in the frequency of 150 kHz, the jamming intensity increased rapidly, and will hold a certain high intensity even reached 11 MHz. Figure 14 is the simulation model based on PSPICE circuit simulation software. In this figure, E1 is the high frequency interference source. This model adopted the activity simulation model in PSPICE. Activity simulation model is an extension of traditional controlled source described by mathematical calculation. Common activity models are saved in ABM.olb [17]. In the simulation model showed in Figure 14, the high frequency inter- ference source of DC motor is modeled by HIPASS. In- put the high frequency interference source in this model as the controlled source. Meanwhile, set a probe on the terminal of 25 resistances which represents LISN, then set up the analysis type as alternating analysis in setting window, and the scale range as 150 kHz - 30 MHz. Figure 15 shows the comparison of simulated and ex- periment spectrum of LISN side common-mode voltage from PSPICE circuit simulation software. From the comparison we could find that simulated spectral curve could follow the experiment one correctly, proved the accuracy of the DC motor model and analysis of inter- ference source. Figure 11. Curve of conduc te d interference sourc e. Figure 12. Equivalent circuit of common mode test. Copyright © 2011 SciRes. EPE  J. F. LIU ET AL. Copyright © 2011 SciRes. EPE 105 Figure 13. Actual spectrum measurement of DC motor. Figure 14. Model of circuit simulation. 7. Conclusions Contemporary research about the equivalent circuit of separated excited DC motor in all EMC frequency is not sufficient. The work this paper accomplished was to re- search the high frequency common-mode equivalent circuit of separately excited DC motor based on the re- search of inner principle of DC motor and steering proc- ess, and determine the parameters by Ant Colony Algo- rithm. This equivalent circuit could be used for analysis and measuring of the motor side common-mode con- ducted EMI emission power and EMI current. Further- more, the similarity of simulation and experiment result has proved its correctness. 8. References Figure 15. Spectrum contrast between simulation and ex- periment of common mode conducted interference in DC machine. [1] N. Mutoh, “A Suitable Method for Ecovehicles to Con-  106 J. F. LIU ET AL. trol Surge Voltage Occurring at Motor Terminals Con- nected to PWM Inverters and to Control Induced EMI Noise,” IEEE Transactions on Vehicular Technology, Vol. 57, No. 4, pp. 2089-2098. doi:10.1109/TVT.2007.912174 [2] J. Benecke, A. Lined and S. Dickmann, “Automatic HF Model Generation and Impedance Optimization for Low Voltage DC Motors,” Proceedings of the 2008 Interna- tional Conference on Electrical Machines, Vilamoura, 6-9 September 2008, pp. 1-6. doi: 10.1108/03321641011061506 [3] K. Maki, H. Funato and L. Shao, “Motor Modeling for EMC simulation by 3-D Electromagnetic Field Analysis,” IEEE International Conference on Electric Machines and Drives Conference, Miami, 3-6 May 2009, pp. 103-108. doi: 10.1109/IEMDC.2009.5075190 [4] C. Martis, H. Hedesiu and B. Tataranu, “High-Frequency Model and Conductive Interferences of a Small Doubly Salient Permanent Magnet Machine,” IEEE International Conference on Industrial Technology, Hammarnet, 8-10 December 2004, pp.1378-1383. doi: 10.1109/ICIT.2004.1490762 [5] J. Meng, W. M. Ma, D. Z. Liu et al., “Time Domain Model and Simulation Analysis of the Conducted EMI for Alternator-Rectifier Systems,” Proceedings of the Chinese Society for Electrical Engineering, Vol. 22, No. 6, 2002, pp. 76-80. [6] J. Benecke and S. Dickmann, “Inductive and Capacitive Couplings in DC Motors with Built-in Damping Chokes,” 17th International Zurich Symposium on Electromagnetic Compatibility, Singapore, 27 February-3 March 2006, pp. 69-72. doi: 10.1109/EMCZUR.2006.214871 [7] L. Wang and Q. D. Wu, “Ant System Algorithm in Con- tinuous Space Optimization,” Control and Decision, Vol. 18, No. 1, 2003, pp. 45-48. [8] A. L. Jennings, R. Ordonez and N. Ceccarelli, “An Ant Colony Optimization Using Training Data Applied to UAV Way Point Path Planning in Wind,” IEEE Swarm Intelligence Symposium, Saint Louis, 21-23 September 2008, pp. 1-8. doi: 10.1109/SIS.2008.4668302 [9] Y. G. Chen, X. Gu, Y. H. Shen and S. Z. Xing, “Optimi- zation of Active Power Filter System PI Parameters Based on Improved Ant Colony Algorithm,” IEEE Inter- national Conference on Mechatronics and Automation, Luoyang, 25-28 June 2006, pp. 2189-2193. doi: 10.1109/ICMA.2006.257633 [10] X. S. Liu, J. J. Qi, Q. T. Song et al., “Method of Con- structing Power Line Communication Networks over Low-Voltage Distribution Networks Based on Ant Col- ony Optimization,” Proceedings of the CSEE, Vol. 28, No. 1, 2008, pp. 71-76. [11] M. X. Yuan, S. N. Wang and P. K. Li, “A Model of Ant Colony and Immune Network and Its Application in Path Planning,” 3rd IEEE Conference on Industrial Electron- ics and Applications, Singapore, 3-5 June 2008, pp. 102- 107. doi:10.1109/ICIEA.2008.4582488 [12] W. Gao, “New Computational Model from Ant Colony,” IEEE International Conference on Granular Computing, Fremont, 2-4 November 2007, p. 640. doi: 10.1109/GrC.2007.26 [13] A. Boglietti, A. Cavagnino and M. Lazzari, “Experimen- tal High Frequency Parameter Idetification of AC Elec- trical Motors,” IEEE Transactions on Applications, Vol. 49, No. 3, 2005, pp. 5-10. [14] R. Kahoul, P. Marcha, Y. Azzouz and B. Mazari, “HF Model of DC Motor Impedance EMC Problems in Auto- motive Applications,” IEEE International Symposium on EMC, Detroit, 18-22 August 2008, pp. 1-5. doi: 10.1109/ISEMC.2008.4652143 [15] J. Benecke and S. Dickmann, “Analytical HF Model of A Low Voltage DC Motor Armature Including Parasitic Properties,” IEEE International Symposium on EMC, Honolulu, 9-13 July 2007, pp. 1-4. doi: 10.1109/ISEMC.2007.250 [16] J. S. Lai, X. D. Huang, E. Pepa and S. T. Chen, “Inverter EMI Modeling and Simulation Methodologies,” IEEE Transactions on Industrial Electronics, Vol. 53, No. 3, 2006, pp. 736-744. doi:10.1109/TIE.2006.874427 [17] D. H. Zhang, P. Yan, Y. H. Gao et al., “Using Methods of Transformer in Pspice,” Electrotechnical Application, Vol. 4, No. 1, 2007, pp. 82-87. Copyright © 2011 SciRes. EPE
|