Journal of Modern Physics, 2011, 2, 379-391
doi:10.4236/jmp.2011.25047 Published Online May 2011 (http://www.SciRP.org/journal/jmp)
Thermodynamic Formulation of Living Systems
and Their Evolution
Luis Felipe del Castillo, Paula Vera-Cruz
Departamento de Polímeros, Instituto de Investigaciones en Materiales, Universidad Nacional
Autónoma de México, Mexico, Mexico
Received January 20, 2011; revised March 7, 2011; accepted April 2, 2011
Abstract
The purpose of this review article is to present some of the recent contributions that show the use of thermo-
dynamics to describe biological systems and their evolution, illustrating the agreement that this theory pre-
sents with the field of evolution. Organic systems are described as thermodynamic systems where entropy is
produced by the irreversible processes, considering as an established fact that this entropy is eliminated
through their frontiers to preserve life. The necessary and sufficient conditions to describe the evolution of
life in the negentropy principle are established. Underlining the fact that the necessary condition requires
formulation, which is founded on the principle of minimum entropy production for open systems operating
near or far from equilibrium, other formulations are mentioned, particularly the information theory, the en-
ergy intensiveness hypothesis and the theory of open systems far from equilibrium. Finally suggesting the
possibility of considering the lineal formulation as a viable alternative; that is, given the internal constric-
tions under which a biological system operates, it is possible that the validity of its application is broader
than it has been suggested.
Keywords: Entropy, Life, Evolution, Dissipative Structures, Negentropy Principle
1. Introduction
The application of thermodynamics [1] to biological
systems and their evolution has offered important con-
tributions [2] by describing the characteristics of animal
evolution [3]. The basic aspect underlined is that the
laws of thermodynamics can predict the feasibility of the
processes and the relation between the variables [4].
Schrödinger established the first contributions to the
field in 1944 [5], offering some ideas about the concept
of negentropy or negative entropy to describe the com-
mon fact that physiological processes gradually generate
an increase of the internal “order” in living organisms. In
the sense that the action of living matter opposes the de-
gradation of the organic constituents by effect of the ir-
reversibilities [6,7].
Currently, the concept of order in relation to negen-
tropy is ignored since a quantitative correlation has not
been found. Alternatively, in biology the equivalence has
been proposed with the concept of “organization” (re-
garding structure), originated in information theory as a
more appropriate way to quantify the degree of structur-
ing (or contained information) of an organic system, as
proposed by Brillouin in 1951 [8,9].
Schrödinger also applied the concept of negentropy to
describe the evolution of species, which has received
much attention [10]. Another related development can be
attributed to Prigogine in 1946 [11], who applied the
theory of linear non-equilibrium thermodynamics to de-
scribe the phenomenon of adaptation of species. He con-
sidered the organism as an open system in stationary
state [7], which evolves in the direction that entropy
production decreases, and reaches a minimum when the
adaptation to the environment has concluded. With these
first attempts, the phenomenon of adaptation was ex-
pressed in a thermodynamic language, involving both
chance and necessity [12], thus being characterized as a
teleonomic [13] phenomenon.
The present work describes the basic facts originated
by the irreversibility in biological systems, and the rele-
vant advances in animal evolution in terms of structure
growth [14] and the introduction of stationary conditions
(maturation process) [15]. Particularly, these two aspects
are formulated in the negentropy principle, which estab-

L. F. DEL. CASTILLO ET AL. 380
lishes the necessary and sufficient conditions for the sur-
vival of a species when the environment has suffered a
radical change that endangers its existence. The suffi-
cient condition is negentropic growth and the necessary
condition observes that the adaptation process (maturity)
is the search and achievement of the stationary state in
the habitat surrounding a species.
Afterward, the contributions to formulate the neces-
sary condition for survival are discussed [11]. Particu-
larly, the information theory, the energy intensiveness
hypothesis, and the theory of self-organization of dissi-
pative structures far from equilibrium.
2. Nature of Living Matter as a
Thermodynamic System
Important efforts have been made to describe biological
systems from the point of view of macroscopic sciences,
particularly thermodynamics and statistical physics
[16,17].
Biological systems are organized internally by con-
strictions. These are internal walls (membranes, epithelia,
endothelia, interfaces, etc) and their role is to maintain
separated two localities, each of them in equilibrium and
specified by different local values of the thermodynamic
variables; particularly, temperature, pressure or electro-
chemical potentials. Generalized flows occur through
these constrictions, such as transport of mass, charge,
calorific energy and momentum [18]. Since the constric-
tions hold the pressure differences, these flows occur
under conditions of mechanical equilibrium, which is
manifested by the absence of accelerations in them [19].
The present description considers the flows and forces
at the local level, such as two entities on both sides of a
cellular membrane (see Table 1). This description is
known as mesoscopic (at the micron scale) and is gov-
erned by the paradigm of mesoscopic systems, charac-
terized by the presence of fluctuations formally described
by the theory of Brownian motion in systems under elec-
tromechanical equilibrium [20].
Assuming that equilibrium thermodynamics condi-
tions prevail around the constrictions, such as cellular
Table 1. Physiological processes are specified as flows pro-
duced by forces.
Generalized Flows (Jj) Forces (Xj)
Diffusive passive 12

  
Diffusive active Coupling forces
Volumetric movement of fluids 12
PPP 
Ion transport 12

  
Advance of chemical reaction Chemical affinity
membranes, then the principle of regression of fluctua-
tions is valid and the system is stable and behaves ac-
cording to the Le Chatelier-Braun principle [21].
Equilibrium thermodynamics prescribes the law of en-
tropy growth when generalized flows [22] occur through
a membrane from locality 1 to locality 2.
12
ddd 0SS S

 (1)
The differential expression for specific entropy is giv-
en by:
11
1
ddd d
j
c
j
j
P
Suv n
TT T



 (2)
In (2) u, v and nj are the internal energy, volume and
number of particles per unit of mass, respectively, asso-
ciated to a locality with c different species. Considering
the presence of two localities separated by a membrane,
the change of total specific entropy is given by the fol-
lowing equation:
12
11
12 12
12
1
1
12
11
ddd
d
jj
cj
j
PP
Su v
TT TT
n
TT



 







(3)
where the laws of conservation of energy, conservation
of volume and conservation of mass have been applied.
12
dd d0uu u

 (4)
12
dd d0vv v

 (5)
12
dd d0nn n

 (6)
Equalities (4-6) indicate that the system is operating
under conditions of isolation (0U, where Uis the
total internal energy).
According to classical thermodynamics, the contribu-
tion to the variation of entropy of each of the terms in (3)
must be positive, as indicated by the Second Law of
Thermodynamics.
11
12
11
dd0Su
TT




 (7)
12
11
12
dd0
PP
Sv
TT




 (8)
12
11
1
12
dd0
jj
cj
j
Sn
TT







 (9)
The validity of conditions (7-9) requires no additional
or external actions influencing the flows or forces de-
scribed, Therefore, the effects expressed in these equa-
tions are considered independent (system regarded as iso-
lated).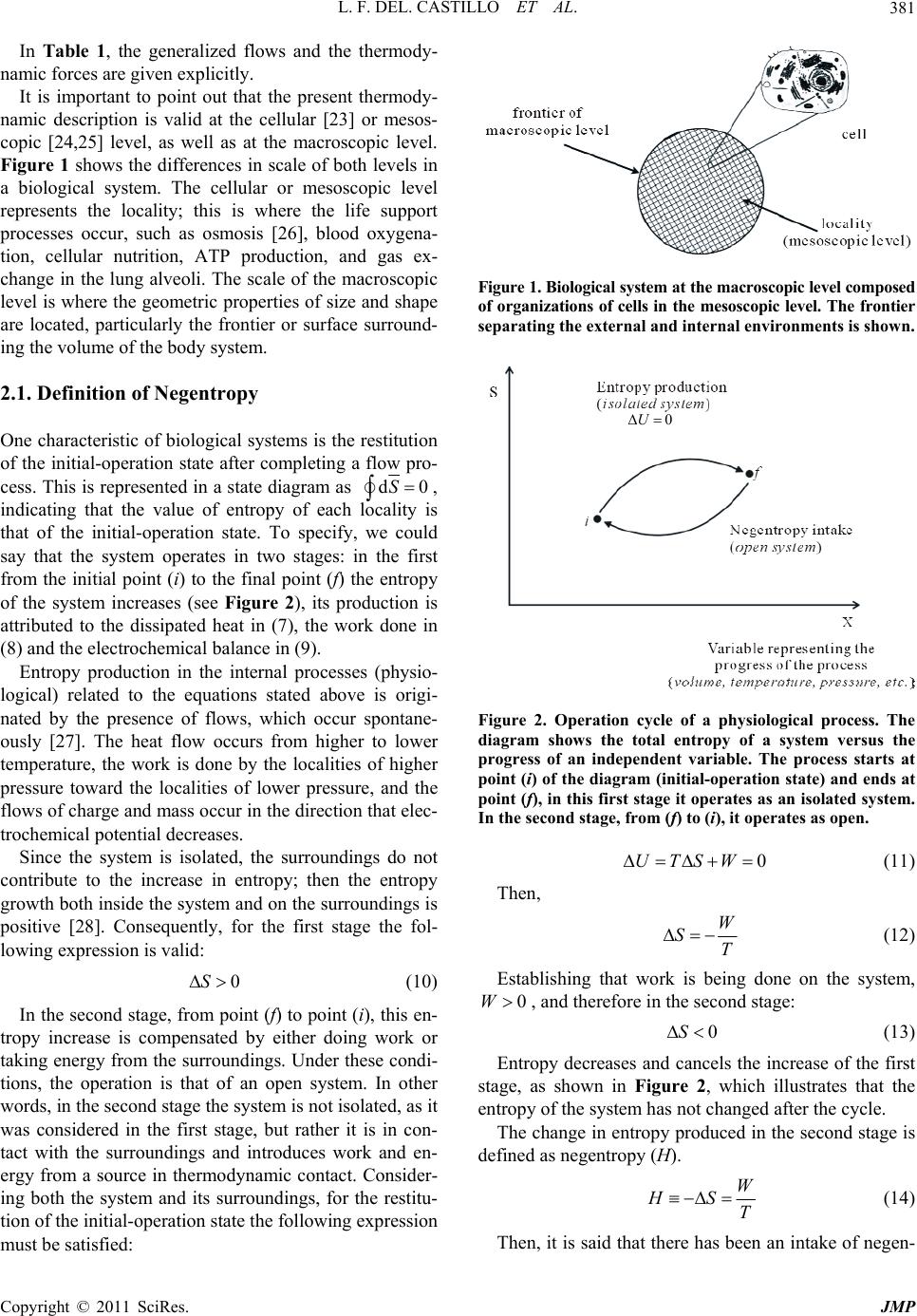

L. F. DEL. CASTILLO ET AL. 381
In Table 1, the generalized flows and the thermody-
namic forces are given explicitly.
It is important to point out that the present thermody-
namic description is valid at the cellular [23] or mesos-
copic [24,25] level, as well as at the macroscopic level.
Figure 1 shows the differences in scale of both levels in
a biological system. The cellular or mesoscopic level
represents the locality; this is where the life support
processes occur, such as osmosis [26], blood oxygena-
tion, cellular nutrition, ATP production, and gas ex-
change in the lung alveoli. The scale of the macroscopic
level is where the geometric properties of size and shape
are located, particularly the frontier or surface surround-
ing the volume of the body system.
2.1. Definition of Negentropy
One characteristic of biological systems is the restitution
of the initial-operation state after completing a flow pro-
cess. This is represented in a state diagram as d0S



,
indicating that the value of entropy of each locality is
that of the initial-operation state. To specify, we could
say that the system operates in two stages: in the first
from the initial point (i) to the final point (f) the entropy
of the system increases (see Figure 2), its production is
attributed to the dissipated heat in (7), the work done in
(8) and the electrochemical balance in (9).
Entropy production in the internal processes (physio-
logical) related to the equations stated above is origi-
nated by the presence of flows, which occur spontane-
ously [27]. The heat flow occurs from higher to lower
temperature, the work is done by the localities of higher
pressure toward the localities of lower pressure, and the
flows of charge and mass occur in the direction that elec-
trochemical potential decreases.
Since the system is isolated, the surroundings do not
contribute to the increase in entropy; then the entropy
growth both inside the system and on the surroundings is
positive [28]. Consequently, for the first stage the fol-
lowing expression is valid:
0S (10)
In the second stage, from point (f) to point (i), this en-
tropy increase is compensated by either doing work or
taking energy from the surroundings. Under these condi-
tions, the operation is that of an open system. In other
words, in the second stage the system is not isolated, as it
was considered in the first stage, but rather it is in con-
tact with the surroundings and introduces work and en-
ergy from a source in thermodynamic contact. Consider-
ing both the system and its surroundings, for the restitu-
tion of the initial-operation state the following expression
must be satisfied:
Figure 1. Biological sy stem at t he macrosc opic level compo sed
of organizations of cells in the mesoscopic level. The frontier
separating the external and internal environments is shown.
0U


Figure 2. Operation cycle of a physiological process. The
diagram shows the total entropy of a system versus the
progress of an independent variable. The process starts at
point (i) of the diagram (initial-operation state) and ends at
point (f), in this first stage it operates as an isolated system.
In the second stage, from (f) to (i), it operates as open.
0UTSW

  (11)
Then,
W
ST

 (12)
Establishing that work is being done on the system,
0W, and therefore in the second stage:
0S

 (13)
Entropy decreases and cancels the increase of the first
stage, as shown in Figure 2, which illustrates that the
entropy of the system has not changed after the cycle.
The change in entropy produced in the second stage is
defined as negentropy (H).
W
HS
T
  (14)
Then, it is said that there has been an intake of negen-

L. F. DEL. CASTILLO ET AL. 382
tropy to the system [29].
On the other hand, a structure growth could have oc-
curred in the system, which can also be described by (10)
and (14) establishing two stages, as mentioned above.
Then, the first stage features the transformation of food
proteins and the ligands produced in the cell, where en-
tropy increases. In the second stage, the structuring of the
produced components involves work (W). Therefore,
there are two types of negentropy intake: one occurs in
the common physiological processes (H1) in the irre-
versible flows, and the other in structure growth (H2).
Thus, the total negentropy intake will be:
12
H
HH (15)
2.2. Dissipative Structures
From the macroscopic point of view, the biological sys-
tem behaves essentially as a dissipative structure, but the
heterogeneity of its internal structure differentiates it
from the physicochemical systems capable of becoming
dissipative structures. For example, a metallic rod con-
nected to two electric poles, kept under isothermal con-
ditions, dissipates to the surroundings an amount of en-
ergy defined by the product of the voltage applied and
the intensity of the electrical current. At this level, the
internal structure of the metal has a microscopic arran-
gement at angstrom-level, much smaller than the scale of
the mesoscopic structure. Another characteristic that se-
parates the dissipative structures of the biological sys-
tems from those of the physicochemical systems [30] is
the ability to grow with time and reproduce itself without
losing this characteristic. For example, the dissipative
structures of Marangoni and Bénard [31,32] operate
without these attributes. However, the biological dissipa-
tive structures [33] can be described by physicochemical
methods, as discussed below.
The cellular formulation for entropy production at the
local level is established according to a balance equation:
d
dSS
S
t
 
J
 (16)
Equation (16) establishes that the gain or loss of en-
tropy per unit volume is equal to the entropy produced
minus the net entropy flow through the surfaces of the
localities. Here, Sjjj
J
X 

is the entropy produc-
tion given by the sum of the tensor products of flows (Jj)
and forces (Xj) present in the localities. The second term
of (16) is the divergence of the flow of entropy that cor-
responds to its net flow through the cellular surface.
Alternatively, considering the macroscopic formula-
tion of the biological system at the global level, by inte-
gration of (16) we find the following expression for the
production and flow of entropy:
ddd
ddd
ie
T
SSS
ttt
 (17)
where,
dd d
dd
T
V
SSv
tt
  (18)
In (18) V is the volume of the biological system.
dd
d
e
S
S
t



J
e (19)
where e is a unit vector pointing in the direction of the
normal of every point of the frontier, indicated by the
surface Σ.
dd
d
i
S
V
Sv
t
  (20)
Considering entropy production for a biological dissi-
pative structure in the global formulation, from Table 2
we have that:
dd
dd
ie
SS
tt
 (21)
Equation (21) is the mathematical expression of the
negentropy principle in the ontogenic scale of a proto-
type. It indicates the requirement for negentropic growth:
that the entropy produced in the system by the internal
Table 2. Some cases where Equations 17-20 are applied
according to the type of system considered.
Type of systemConditions Relations of S
(cellular for-
mulation)
Relations of
entropy S
(global for-
mulation)
Thermodynamic
system
Isolated (strict
validity of the
second law of
thermodynam-
ics)
0
S
 J
d0
dS
S
t
  
0
S

reversible
process
d0
d
eS
t

dd
0
dd
i
T
SS
tt


Physicochemical
dissipative
structure
Open system
with
elimination of
produced
entropy
d0
d
S
t
 
0
SS
 J 
0
S

reversible proc-
ess
dd
dd
ie
SS
tt

Biological
dissipative
structure
Open system
with
elimination of
entropy and
structure
growth
d0
d
S
t
 
SS

J

dd
dd
ie
SS
tt


L. F. DEL. CASTILLO ET AL. 383
processes and that generated by the growth of the proto-
type are eliminated through the frontiers [34]. The need
to eliminate the entropy produced in the internal envi-
ronment of biological systems denotes a principle of sur-
vival.
Describing Figure 3, the biological system distances
itself from the homogeneous or uniform system, thus
behaving as a heterogeneous system (survival line). For
this to occur, entropy production of the biological sys-
tems must be eliminated through the intake of negen-
tropy (energy and work to maintain the structure). Living
matter evades [35] decay to the homogeneity since or-
ganisms evidently feed on negative entropy to restore the
initial-operation state. The difficulties produced by in-
ternal and external environments are manifested by a
change from the survival line to the line of maximum en-
tropy of the homogeneous system, where stress indicates
the appearance of survival risk. The stress fluctuations [36]
represent the difficult situations experienced by a bio-
logical system, these are reflected on the survival line as
perturbations either to the structure or to the physiologi-
cal functions, and as such are followed by the regression
of fluctuations as established by the Le Chatelier-Braun
principle of stability applied to biological structures. This
principle states that upon a perturbation, systems react
against it to return to the initial-operation state. In a
broader sense, the same thing occurs when there is dam-
age to the structure, showing the capacity of biological
systems to self-regenerate [37]. The accumulation of
stress indicates the presence of the process of aging [38],
manifesting an increase in vulnerability to external per-
turbation (senescence [39,40]), which will result in the
breakpoint and ultimately in death when there are no
conditions to return the system towards its initial-opera-
tion state. The cumulative effect of stress preceding the
breakpoint (see asterisk-line in Figure 3) shows a dete-
rioration of the physiological functions present in aging.
3. The Principle of Evolution: The
Negentropy
The problem of explaining the evolution of species
[41,42] raises the question about the mechanism of ad-
aptation of living organisms to the environment [43].
This section is dedicated to establishing the thermody-
namic description of adaptation, showing that evolution
can be described as a kinetic phenomenon.
To describe evolution it is necessary to change the de-
scriptive scale from the prototype or ontogenic scale to
the collective or phylogenic [10] scale. Figure 4 shows the
levels of entropy production, pointing out the qualitative
changes present in each scale. For the phylogenic proc-
esses entropy production is associated to a collective, thus
the evolutive processes are established at this time scale.
Figure 3. The line of maximum of entropy versus time is shown for a homogeneous system (where all the molecules of an or-
ganism form a liquid-like mixture); and for a heterogeneous syste m, organized with internal constrictions (organs and flesh).
The dotted line represents the difference between the maximums of entropy of the homogeneous and heterogeneous systems.
This difference is equal to the negentropy required to maintain constant the acquired structure and avoid death (survival
line). Note that the structure remains constant until the breakpoint.

L. F. DEL. CASTILLO ET AL. 384
Figure 4. The different scales of time and entropy produc-
tion in different systems, from the mesoscopic or celular
scale to the phylogenic scale.
Thermodynamically, the evolution of living matter is
described by postulating the validity of the negentropy
principle [44], which establishes that the evolution of bio-
logical systems occurs in the direction [45] that the
structure [46] becomes more complex. That is, the phy-
logenic changes occur in the direction that the negen-
tropy of the structure increases.
However, this postulate represents the sufficient con-
dition, since it only shows the need to evolve by gaining
structuring; moreover, the adaptation must be established
simultaneously, when the system has adjusted to the en-
vironment in a stable condition.
The negentropy principle can be associated with the
inherent difficulty that the growth of the system escalates
in size [47] and shape [48-50], and particularly it is
found that entropy production increases with volume
[51,52,3] (V), as shown by the expression for internal
entropy production

dd
iSt according to (20). In con-
trast, the elimination of the entropy of the system

dd
eSt depends on the area of the frontier (Σ), as seen
in (19). Finally, the evolutionary structuring of the sys-
tem does not occur in accordance with the volume
growth of the species, but rather a balance between size
and shape must be maintained for an efficient elimina-
tion of produced entropy. Then, it is clear that growth is
governed by thermodynamics. Particularly, the rate of
entropy elimination with increasing body mass obeys the
power law (with 0.75 instead of 1). Figure 5 shows how
evolution has made more efficient the negentropy intake
and entropy elimination without increasing the surface of
the system [53].
One possible formulation of the necessary condition for
survival is the adaptation of species to the environment,
so as to minimize entropy production [54,55]. This can
be established by the condition that the system operates
Figure 5. How evolution has made more efficient the negen-
tropy intake and entropy elimination without increasing the
surface of the system.
under stationary conditions. According to the require-
ments of thermodynamics, for the fulfillment of this
principle it is necessary that, at least for a given period of
time, the action of a species be specifically coupled to its
ecological surroundings [56-62] in a way that its relation
with the environment does not change during this period
of time. With this, efficiency is achieved in both energy
consumption and entropy elimination: the metabolism
reaches maximum efficiency.
In the evolution of the species two parallel and inde-
pendent events occur, as illustrated in Figure 6. These
processes are the growth of the organic structure and the
adaptation to the environment.
The evolution pathway [65] is guided by natural selec-
tion through the active mechanisms of heritage between
generations in k steps [66-68]. In Figure 6, the arrows
indicate the step from one generation to the next. This
process leads to an increase in the demographic survival
capacities [17]. It has been established that the evolutive
process implies many generations and many events of
Figure 6. The negentropy principle in terms of an evolution
pathway. The adaptation process is established in k steps,
where 1k to produce a stationary state between the
prototypes of a species and the environment. The dashed
line with white circles shows the separation between the
species and the environment that produced the stress
[63,64]; for the k generation the stress becomes cero.

L. F. DEL. CASTILLO ET AL. 385
combination and recombination of DNA between mem-
bers of a large group. Then, the groups that failed to
evolve in k steps, in accordance with the negentropy
principle, have disappeared from the environment. In this
sense, natural selection relates the two aspects: structure
growth and the course of adaptation.
Regarding the sufficient condition of the negentropy
principle, the evolution appears to be continuous. How-
ever, from the molecular point of view [69], it is a se-
quence of jumps occurring stochastically.
Concerning the formulation of the necessary condition
of the negentropy principle, it has been established in
two ways: firstly by using the principle of minimum en-
tropy of linear non-equilibrium thermodynamics; and se-
condly by the self-organization of dissipative structures
far from equilibrium. This last point will be discussed in
the next section.
In relation to the principle of minimum entropy of
non-equilibrium thermodynamics, it shows the require-
ments for the transport coefficients to be constant and the
flow-force relations to be linear. The first requirement is
fulfilled by the condition that during a long enough pe-
riod of time the physiological capabilities acquired do
not change significantly. On the other hand, the linearity
is satisfied by the requirement that evolution has mini-
mized the gradients under which life operates.
This is evidenced by two facts of the operation of phy-
siological processes: first that they occur near electro-
mechanical equilibrium; and second that they occur in
nearly isothermal conditions in the internal environment
of the system without taking into account the variations
of the external environment, since they are controlled at
the frontier (composed of the skin and its coat), as shown
in Figure 7.
4. Parallel Formula tions
The negentropy principle formulated in the previous
T
μ
0
S
 
s
J

Figure 7. Production of entropy occurs internally and the
entropy flow occurs at the frontier. In average, the station-
ary state condition prevails internally.
section describes the evolution of life as a dissipative
structure regulated by entropy production, its elimination
from the system [70], and the adaptation to the environ-
ment. Parallel to this formulation, other alternatives pre-
senting basic relations with thermodynamics have been
established, such as information theory [71,72], the en-
ergetic formulation of biological structures, and the the-
ory of self-organization of complex systems far from
equilibrium. These are not contrasting formulations but
rather complementary aspects, since they highlight the
kinetic descriptions that thermodynamics does not spec-
ify within its own context, which are important aspects to
explain the evolution of species. They are described be-
low.
4.1. Information Theory
According to information theory, entropy is defined by
the following summation:

1ln
j
j
j
Spp


 (22)
where j indicates the number of each element involved in
the information set representing the system, with the
probability of occurrence pj. The factor  is the total
number of elements or complexions [8,9] in the set. The
difficulty of applying this theory to biological systems
lays in having to fully describe the details of the system
within a numbered information set [73,74], since gener-
ally  is very large. The information is a quantity related
to a physical state [75].
A similar difficulty is found in statistical physics when
defining entropy, which is overcome by using an algo-
rithm that counts the number of microstates that are ac-
cessible to the system, thanks to the simplifying hy-
pothesis that all the elements in the representative set
have an equal probability [76]. In that case, if 1
j
p


then lnS

 (note that the entropy is a nondimen-
sional quantity) [77].
For biological systems all probabilities are not neces-
sarily equal, in fact they could even change with time
since these systems operate irreversibly. It is thanks to
modeling that the information contents of a biological
system have been described, providing an insight to the
characteristics of the evolution of life [78].
Recent advances in this direction highlight the
achievements using evolutionary models that combine
mutations and mechanisms of speciation [79,80]. Some
bibliographic sources have referred to the feedback be-
tween the prototype and the environment as cybernetic
[81] aspect of evolutionary mechanisms.
Significant progresses have occurred in the analysis of
biological entities of small dimensions, as is the case of
DNA [82-85] and other cell components, down to the

L. F. DEL. CASTILLO ET AL. 386
description of the cell itself [23,86].
Information theory gives a partial quantitative evalua-
tion of the degree of organization [87], preserving the
meaning of entropy according to statistical physics [88].
In fact, the increase of S corresponds to a loss of uncer-
tainty; the approach dealt here indicates the lack of in-
formation. The same occurs with thermodynamic theory,
where irreversibility, counted as ΔS, is also associated
with the degradation of the useful energy to restore the
initial-operation state after spontaneous processes occur,
which can be interpreted as a loss of information. Along
these lines, based on information theory, the interpreta-
tion of entropy-increase is linked to the increase of dis-
organization for biological systems. Therefore, the ne-
gentropy principle is reflected as an increase in the en-
abled organization and system functions, indicating the
presence of greater organization.
Consequently, evolution is directed (teleonomy [13])
in the direction that organization increases. In this sense,
the adaptation to an environment requires an increase in
information and a greater efficiency in handling it (that is
the meaning of the negentropy [89]).
However, the connection between the concepts of en-
tropy in information theory and thermodynamics is lack-
ing. To achieve a quantitative comparison between these
concepts, it is necessary to relate the probabilities used as
measures of certainty with the thermodynamic variables
of internal energy and the parameters that specify the
constriction of the system. What stands out successfully
in the theory of evolution is the relationship between
organization and negentropy [90,7].
4.2. Energy Intensiveness Hypothesis
The intensiveness of energy consumption of a species
can provide an evolutionary pattern as selection criteria
in the evolution of species [91,92]. This relates to bio-
logical evolution by considering the interactions between
species of the same environment, particularly the ability
to find, consume and guard resources as the dominant
aspect of such evolution. According to this hypothesis it
is the capacity to process energy (escalation), which has
been a requirement given the critical situations that some
species have faced [93]. Rigorously speaking, the negen-
tropy principle is not contradicted, since the processing
of energy and its conversion to work, as well as the ca-
pacity to discard part of the energy, is the way to con-
ceive a biotic machine [23] that can operate under condi-
tions of irreversibility, thus satisfying this principle.
The relation between the energy intensiveness approach
and negentropic growth becomes clear from the fact that
biological systems obtain energy from the exterior, such
as the sun, and store the available energy inside their struc-
ture as negentropy [94]. From this point of view, biodi-
versity multiplies modes of energy consumption [95], and
life evolution manifests itself by increased complexity
[96], energy-gathering metabolic systems [97], teleonomic
[13] character, as well as its abundance and diversity.
4.3. Self-Organization of Dissipative Structures
According to the nonlinear hydrodynamic stability the-
ory [98-101] and the description of coupled chemical
reactions by chemical kinetics [102-104], dissipative
structures as open systems outside equilibrium are capa-
ble of self-organization and forming structural patterns
[105,106] depending on the boundary conditions im-
posed on the system [107].
The hypothesis that the same occurs for biological
systems with a higher level of complexity has helped to
establish new theoretical developments to explain both
the origin of life as well as the diversity of species. Re-
ferred to as chaos theory [108,109], it describes dissipa-
tive structures capable of transforming themselves
through a mechanism of time-space symmetry breaking.
The new structures emerge in a point called bifurcation,
after critical fluctuations, where several branches or pos-
sibilities of pattern formation appear (see Figure 8).
Natural selection could choose one of the branches in-
fluenced by the environment (adaptation requirement) or
simply any possibility of change could present itself
(probabilistic requirement for diversity).
The continuous transition towards a specific branch is
possible, called “transitional bifurcation” [110,111]. This
is also a result of self-organization at the edge of chaos
[112]. In addition, some systems may show self-organi-
zation of the first or second kind depending on boundary
Figure 8. The possibilities of evolution of a system near
equilibrium affected by an environmental crisis, it goes
through long fluctuations and a bifurcation is produced to
reach a new evolutionary branch to overcome the need for
adaptation.

L. F. DEL. CASTILLO ET AL. 387
and initial conditions [113], they can also exhibit the
development of complex hierarchical structures [114,115].
So far, the basic postulation of negentropic growth that
negentropy intake is the cause for structure growth is still
valid. However, kinetic formulations have sought to re-
place the minimum dissipation principle for a broader
one that explains not only adaptation but also the causes
of evolution.
5. Discussion
The thermodynamic description of the vital processes
and their evolution is quantitative for the physiological
processes in the mesoscopic scale, the global scale for a
prototype, but qualitative in the phylogenic scale of the
species. In the mesoscopic scale an endless row of phy-
siological processes occur that in the ontogenic or global
scale appear as a continuum. Then, it makes sense to talk
about the entropy associated with a heterogeneous bio-
logical system with its maximum compatible with the
internal constraints, which are represented by the internal
energy barriers established in the organization of the
system. This entropy is lower than that which the same
molecules would have if they were arranged homogene-
ously in a liquid-like mixture. The difference between
both amounts is the negentropy associated to the organic
structure; it is interpreted as the amount of work or heat
energy required to restore the initial-operation state. At
the same time, to maintain the organic structure invariant,
the entropy produced in the physiological processes
when they reproduce the irreversible thermodynamic
flows must be eliminated to avoid producing stress and
risking life. This is how survival and proximity to death
(breakpoint) are defined.
On these bases, the thermodynamic image of life is
that of a system that develops a cycle, with entropy pro-
duction on one part and elimination on the other closing
the cycle. Emphasizing the process of elimination, or-
ganic systems are regarded as dissipative structures
highly organized both mesoscopically and globally. The
previous image is centered on the ontogenic scale. Re-
garding the phylogenic, the time scale widens to contain
biological changes in a time period much longer than the
duration of a generation of prototypes of a species. In the
preceding thermodynamic terms, the negentropy princi-
ple is established with two requirements: an increase in
organic structuring over time, and the establishment of a
stationary state of high metabolic efficiency (minimum
production of wasted energy). The determining factor of
the negentropy principle is that one cannot be achieved
without the other (necessary and sufficient conditions).
The second requirement is set in a state of minimum en-
tropy production in relation to a stationary one, thus gu-
aranteeing the property of the regression of fluctuations,
ensuring the survival of the species.
The negentropy principle has been considered ade-
quate for describing the general aspects of living matter
and its evolution. At present, this principle is established
as a biological law due to its general validity.
The mechanisms proposed in the linear
non-equilibrium thermodynamic description of adapta-
tion to an environment through the establishment of a
minimum dissipation stationary state are a good proposal.
So much so, that attempts have been made to extend their
validity to the stationary case far from equilibrium, cre-
ating a new insight to search for a nonlinear theory for
biological systems.
Currently, there are several ideas that treat the evolu-
tion of life and they postulate structural growth as the
motor of evolution. However, the limitations to growth
have been scarcely foreseen except for the criticism to
Cope’s rule due to the advantages in volume growth. In
this direction, the restrictions due to the surface increase
of biological bodies are a topic that could be discussed in
the future. The energy intensiveness hypothesis is similar
regarding the capacity to process energy from the habitat.
Nevertheless, it is not possible to generate or consume
energy without wasting some to be removed as excess
entropy, but it remains the key to achieve efficiency and
even equally important, the survival of the species. The
most appropriate critical view is thus established from
the thermodynamic point of view, where the two aspects
are included in the negentropy principle.
In contrast, information theory, using Brillouin’s defi-
nition of entropy, gives a new interpretation to thermo-
dynamic entropy with its own methodology to measure it
for small biological organisms, both at the microscopic
and mesoscopic scales. The achievements show the de-
scriptive capabilities of the theory. It is expected to
achieve a more complete description of the principle of
entropy balance on the phylogenic scale with the devel-
opments in the techniques of advanced Monte Carlo
[116], to verify the negentropy principle using informa-
tion theory.
The kinetic theory of chaos provides several possibili-
ties of results that describe the change of stable dissipa-
tive structures far from equilibrium. Two things are im-
plicit: that evolution is continuous since the boundary
conditions provide the information of mutations, and that
the choice of one of the many predictions could be de-
termined by natural selection. The image of evolution is
that the adaptation process is a branch of a solution of a
set of differential equations. This is interesting, since it
shows a new insight from the kinetic point of view, which
thermodynamics cannot describe. This is a plausible idea
and contributions in this direction will be welcome.

L. F. DEL. CASTILLO ET AL. 388
Finally, it has been suggested to consider the social
and cultural products of men, both social (work division
and language) and intellectual in sciences and arts, as
part of the characteristics of animal evolution guided by
the principle of negentropic growth. In this sense, the
evolutionary properties are transferred to those products
in terms of the increase of organizational and hierarchi-
cal levels [117] and differentiation [118], highlighting
the abilities to transfer information and knowledge [119].
6. Conclusion
In the present work the nature of biological systems was
described from a thermodynamic point of view. Two
aspects of living matter have been identified. The first
refers to mesoscopic aspects, which describe thermody-
namically the physiological processes at the level of a
cell or local scale, where entropy production is generated
by the presence of irreversible flows. The second relates
to the macroscopic aspects in the global scale, where the
elimination of entropy through the surface of the bodies
occurs, thus operating as open systems. At this level, the
organization of a biological system is identified by the
number of constrictions; which are equivalent to entropy
reducers. The total provides the negentropy of the system.
Regarding the division of the time scale, two are iden-
tified: the ontogenic or the evolution of the prototype,
and the phylogenic or the evolution of the species. In the
ontogenic description there is a difficulty to restore the
initial-operation state at the presence of stress; therefore
a regression of fluctuations is required for maintaining
the structure. The difficulty arises when stress accumu-
lates, since the entropy produced by physiological proc-
esses is not being eliminated from the system and there is
no negentropy intake, then the open system has been
blocked and is operating like a closed system, which could
result in death. In the phylogenic description, the need
for adaptation is established in the principle of minimum
dissipation and maximum metabolic efficiency. Both evo-
lutionary aspects are included in the negentropy principle.
Moreover, the negentropy principle links two aspects:
the necessity of adaptation to prevent the collective death;
and the probabilistic aspect where mutations occur ran-
domly or induced by the need of survival, enhancing the
possibility of adaptation.
Regarding the validity of the negentropy principle, in
particular with the assumption of minimum energy dis-
sipation, several efforts have been made to go beyond lin-
ear equilibrium thermodynamics and improve its formu-
lation. Encouraging results have been obtained, like those
found in information theory, the energy intensiveness
hypothesis, and the nonlinear stability theory of dissipa-
tive structures far from equilibrium. In all these cases,
the description of biological systems and their evolution
is a task that is far from being finished.
7. Aknowledgements
The authors acknowledge the financial support provided
by DGPA-UNAM (Project IN112109).
8. References
[1] D. Dix, “Toward a Definition of Life: Semantic and
Thermodynamic Considerations,” Journal of Theoretical
Biology, Vol. 102, No. 2, 1983, pp. 337-340.
doi:10.1016/0022-5193(83)90371-5
[2] J. S. Wicken, “Entropy and Evolution: Ground Rules for
Discourse,” Systematic Zoology, Vol. 35, No. 1, 1986, pp.
22-36. doi:10.2307/2413288
[3] D. W. McShea, “Possible Largest-Scale Trends in Organ-
ismal Evolution: Eight ‘Live Hypotheses’,” Annual Review
of Ecology and Systematics, Vol. 29, 1998, pp. 293-318.
doi:10.1146/annurev.ecolsys.29.1.293
[4] J. Kestin, “A Course in Thermodynamics,” 2nd Edition,
McGraw-Hill, New York, 1979.
[5] E. Schrödinger, “What is Life? Mind and Matter,” Cam-
bridge University Press, Cambridge, 1944.
[6] L. Demetrius, “Directionality Principles in Thermody-
namics and Evolution,” Proceeding of the National
Academy of Sciences of the USA, Vol. 94, 1997, pp.
3491-3498. doi:10.1073/pnas.94.8.3491
[7] H. B. Hollinger and M. J. Zenzen, “An Interpretation of
Macroscopic Irreversibility within the Newtonian Frame-
work,” Philosophy of Science, Vol. 49, No. 3, 1982, pp.
309-354. doi:10.1086/289065
[8] L. Brillouin, “Maxwell’s Demon Cannot Operate: Infor-
mation and Entropy. I,” Journal of Applied Physics, Vol.
22, No. 3, 1951, pp. 334-337. doi:10.1063/1.1699951
[9] L. Brillouin, “Physical Entropy and Information. II,”
Journal of Applied Physics, Vol. 22, No. 3, 1951, pp.
338-343. doi:10.1063/1.1699952
[10] M. Ruse, “Monad to Man: The Concept of Progress in
Evolutionaty Biology,” Harvard University Press, Mas-
sachusetts, 1996.
[11] I. Prigogine and T. M. Wiame, “Biologie et Thermody-
namique del Phénomènes Irréversibles,” Experientia (Ba-
sle), Vol. 2, 1946, pp. 451-453.
[12] F. Crick, “Life Itself: Its Origin and Nature,” Simon and
Schuster, New York, 1981.
[13] J. Monod, “Chance and Necessity,” Random, New York,
1972.
[14] M. Rossignol, L. Rossignol, R. A. A. Oldeman and S.
Bensine-Tizroutine, “Struggle of Life or the Natural His-
tory of Stress and Adaptation,” Treemail, The Nether-
lands, 1998.
[15] B. McDowell, “An Examination of the Ecosystems Per-
spective in Consideration of New Theories in Biology

L. F. DEL. CASTILLO ET AL. 389
and Thermodynamics,” Journal of Sociology and Social
Welfare, Vol. 21, No. 2, 1994, pp. 49-68.
[16] J. G. Miller, “Living Systems: Basic Concepts,” Behav-
ioral Science, Vol. 10, No. 3, 1965, pp. 193-237.
doi:10.1002/bs.3830100302
[17] M. T. Hannan and J. Freeman, “The Population Ecology
of Organizations,” The American Journal of Sociology,
Vol. 82, No. 5, 1977, pp. 929-964. doi:10.1086/226424
[18] H. B. Callen, “Thermodynamics and an Introduction to
Thermostatistics,” 2nd Edition, John Wiley & Sons, New
York, 1960.
[19] A. Katchalsky and P. F. Curran, “Nonequilibrium Ther-
modynamics in Biophysics,” Harvard University Press,
Massachusetts, 1981.
[20] A. B. Pippard, “Elements of Classical Thermodynamics,”
Cambridge University Press, Cambridge, 1957.
[21] L. D. Landau and E. M. Lifshitz, “Statistical Physics,”
3rd Edition, (Part I by E. M. Liftshitz and L. P. Pi-
taevskii), Pergamon Press, Oxford, 1980.
[22] G. Lebon, D. Jou and J. Casas-Vázquez “Understanding
non-equilibrium Thermodynamics. Foundations, Appli-
cations, Frontiers”, Springer-Verlag, Berlin, 2008.
doi:10.1007/978-3-540-74252-4
[23] E. B. Jacob, Y. Shapira and A. I. Tauber “Seeking the
Foundations: From Schrödinger’s Negative Entropy to
Latent Information,” Physica A, Vol. 359, 2006, pp.
495-524. doi:10.1016/j.physa.2005.05.096
[24] J. M. Rubi, “The Non-Equilibrium Thermodynamics
Approach to the Dynamics of Mesoscopic Systems,”
Journal of Non-Equilibrium Thermodynamics, Vol. 29,
No. 4, 2004, pp. 315-325. doi:10.1515/JNETDY.2004.058
[25] D. Reguera, J. M. Rubí and J. M. Vilar, “The Mesoscopic
Dynamics of Thermodynamic Systems,” Journal of
Physical Chemistry B, Vol. 109, No. 46, 2005, pp. 21502-
21515. doi:10.1021/jp052904i
[26] L. F. del Castillo, “El Fenómeno Mágico de la Ósmosis,”
Colección Ciencia para Todos, Vol. 16, Fondo de Cultura
Económica, México, 1996.
[27] M. W. Zemansky and R. H. Dittman, “Heat and Thermo-
dynamics: An Intermediate Textbook,” 6th Edition,
McGraw-Hill, New York, 1981.
[28] D. ter Haar and H. Wergeland, “Elements of Thermody-
namics,” Addison-Wesley Publishing Company, Massa-
chusetts, 1966.
[29] L. Brillouin, “The Negentropy Principle of Information,”
Journal of Applied Physics, Vol. 24, No. 9, 1953, pp.
1152-1163. doi:10.1063/1.1721463
[30] V. M. Zhukovsky, “Thermodynamics of Environment,”
Journal of Mining and Metallurgy B, Vol. 36, No. 1-2,
2000, pp. 93-102.
[31] R. Swenson and M. T. Turvey, “Thermodynamic Reason
for Perception-Action Cycles,” Ecological Psychology,
Vol. 3, No. 4, 1991, pp. 317-348.
doi:10.1207/s15326969eco0304_2
[32] M. G. Velarde and C. Normand, “Convection,” Scientific
American, Vol. 243, No. 1, 1980, pp. 93-108.
[33] C. M. Visser and R. M. Kellogg, “Biorganic Chemistry
and the Origin of Life,” Journal of Molecular Evolution,
Vol. 11, No. 2, 1978, pp. 163-169.
doi:10.1007/BF01733891
[34] H. F. Blum, “Time’s Arrow and Evolution,” 3rd Edition,
Princeton University Press, Princeton, 1968.
[35] G. Stent, “That was the Molecular Biology that was,”
Science, Vol. 160, No. 3826, 1968, pp. 390-395.
doi:10.1126/science.160.3826.390
[36] W. Arthur, “Mechanisms of Morphological Evolution: A
Combined Genetic, Developmental and Ecological Ap-
proach,” John Wiley & Sons, Chichester, 1984.
[37] B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and
P. Walter, “Universal Mechanisms of Animal Develop-
ment,” Molecular Biology of the Cell, 4th Edition, Gar-
land Science, New York, 2002.
[38] W. M. Bortz II, “Aging as Entropy,” Experimental Ger-
ontology, Vol. 21, No. 4-5, 1986, pp. 321-328.
doi:10.1016/0531-5565(86)90039-2
[39] W. Arthur, “Theory of the Evolution of Development,”
John Wiley & Sons, New York, 1988.
[40] O. Toussaint, P. Dumont, J. F. Dierick, T. Pascal, C.
Frippiat, F. Chainiaux, F. Sluse, F. Eliaers and J. Remacle,
“Stress-Induced Premature Senescence. Essence of Life,
Evolution, Stress, and Aging,” Annals of the New York
Academy of Sciences, Vol. 908, 2000, pp. 85-98.
doi:10.1111/j.1749-6632.2000.tb06638.x
[41] C. Darwin, “On the Origin of Species,” John Murray,
London, 1859.
[42] D. J. Depew and B. H. Weber, “Darwinism Evolving
Systems Dynamics and the Genealogy of Natural Selec-
tion,” The MIT Press, Cambridge, 1996.
[43] J. Wu and W. Gao, “Spatial Patterns of Species Richness:
A Hierarchical Perspective,” Chinese Biodiversity, Vol. 3,
1995, pp. 12-21.
[44] R. E. Ulanowicz and B. M. Hannon, “Life and the Pro-
duction of Entropy,” Proceedings of the Royal Society of
London B, Vol. 232, No. 1267, 1987, pp. 181-192.
doi:10.1098/rspb.1987.0067
[45] M. Ziehe and L. Demetrius, “Directionality Theory: an
Empirical Study of an Entropic Principle in Life-History
Evolution,” Proceedings of the Royal Society B, Vol. 272,
No. 1568, 2005, pp. 1185-1194. doi:10.1098/rspb.2004.3032
[46] I. Prigogine, “Time, Structure and Fluctuations,” Science,
Vol. 201, No. 4358, 1978, pp. 777-785.
doi:10.1126/science.201.4358.777
[47] D. W. Hone and M. J. Benton, “The Evolution of Large
Size: How does Cope’s Rule Work?” Trends in Ecology
& Evolution, Vol. 20, No. 1, 2005, pp. 4-6.
doi:10.1016/j.tree.2004.10.012
[48] J. G. Kingsolver and D. W. Pfennig, “Individual-Level
Selection as a Cause of Cope’s Rule of Phyletic Size In-
crease,” Evolution, Vol. 58, No. 7, 2004, pp. 1608-1612.
doi:10.1111/j.0014-3820.2004.tb01740.x
[49] B. van Valkenburgh, X. Wang and J. Damuth, “Cope’s
Rule, Hypercarnivory, and Extinction in north American
Canids,” Science, Vol. 306, No. 5693, 2004, pp. 101-104.

L. F. DEL. CASTILLO ET AL. 390
doi:10.1126/science.1102417
[50] J. A. Finarelli, “Testing Hypotheses of the Evolution of
Encephalization in the Canidae (Carnivora, Mammalia),”
Paleobiology, Vol. 34, No. 1, 2008, pp. 35-45.
doi:10.1666/07030.1
[51] J. T. Bonner, “The Evolution of Complexity by Means of
Natural Selection,” Princeton University Press, New Jer-
sey, 1988.
[52] M. T. Carrano, “Body-Size Evolution in the Dinosauria,”
In: M. T. Carrano, R. W. Blob, T. J. Gaudin and J. R.
Wible, Eds., Amniote Paleobiology: Perspectives on the
Evolution of Mammals, Birds, and Reptiles, University of
Chicago Press, Chicago, 2006, pp. 225-268.
[53] D. Jou, J. E. Llebot and C. G. Perez, “Fisica para Cien-
cias de la Vida,” 2nd Edition, McGraw Hill Interameri-
cana, Madrid, 2008.
[54] I. Prigogine, “Introduction to the Thermodynamics of
Irreversible Processes,” Wiley & Sons, New York, 1955.
[55] S. R. de Groot, “Thermodynamics of Irreversible Proc-
esses,” North-Holland Publishing Company, Amsterdam,
1966.
[56] F. J. Ayala, “The Concept of Biological Progress,” In: F.
J. Ayala and T. Dobzhansky, Eds., Studies in the Phi-
losophy of Biology: Reductionism and Related Problems,
Macmillan, New York, 1974, pp. 339-354.
[57] D. C. Fisher, “Progress in Organismal Design,” In: D. M.
Raup and D. Jablonski, Eds., Patterns and Processes in
the History of Life, Springer, Berlin, 1986, pp. 99-117.
[58] J. S. Huxley, “Evolution: The Modern Synthesis,” Harper,
New York, 1942.
[59] J. W. Valentine, “Patterns of Taxonomic and Ecological
Structure of the Shelf Benthos during Phanerozoic Time,”
Palaeontology, Vol. 12, 1969, pp. 684-709.
[60] G. G. Simpson, “The Meaning of Evolution,” Yale Uni-
versity Press, New Haven, 1967.
[61] D. M. Raup, “Testing the Fossil Record for Evolutionary
Progress,” In: M. Nitecki, Ed., Evolutionary Progress,
Chicago University Press, Chicago, 1988, pp. 293-317.
[62] F. J. Ayala, “Can ‘Progress’ be Defined as a Biological
Concept?” In: M. Nitecki, Ed., Evolutionary Progress,
Chicago University Press, Chicago, 1988, pp. 75-96.
[63] H. Selye, “A Syndrome Produced by Diverse noxious
Agents,” Nature, Vol. 138, 1936, p. 32.
doi:10.1038/138032a0
[64] H. Selye, “The General Adaptation Syndrome and the
Diseases of Adaptation,” Journal of Clinical Endocri-
nology, Vol. 6, No. 2, 1946, pp. 117-230.
doi:10.1210/jcem-6-2-117
[65] R. S. Boardman and A. H. Cheetham, “Degrees of Col-
ony Dominance in Stenolaemate and Gymnolaemate
Bryozoa,” In: R. S. Boardman, A. H. Cheetham and W. A.
Oliver, Eds., Animal Colonies: Development and Func-
tion through Time, Dowden, Hutchinson & Ross,
Stroudsburg, 1973.
[66] S. J. Gould, “Wonderful Life,” Norton, New York, 1989.
[67] P. D. Gingerich, “Quantification and Comparison of
Evolutionary Rates,” American Journal of Science, Vol.
293, 1993, pp. 453-478. doi:10.2475/ajs.293.A.453
[68] W. Scharloo, “Canalization: Genetic and Developmental
Aspects,” Annual Review of Ecology and Systematics,
Vol. 22, 1991, pp. 65-93.
doi:10.1146/annurev.es.22.110191.000433
[69] R. Lewin, “Patterns in Evolution: The New Molecular
View,” W. H. Freeman & Company, New York, 1999.
[70] J. S. Wicken, “Thermodynamics and the Conceptual
Structure of Evolutionary Theory,” Journal of Theoreti-
cal Biology, Vol. 117, No. 3, 1985, pp. 363-383.
doi:10.1016/S0022-5193(85)80149-1
[71] C. Shannon, “A Mathematical Theory of Communica-
tion,” Bell System Technical Journal, Vol. 27, 1948, pp.
379-423, 623-656.
[72] E. T. Jaynes, “Information Theory and Statistical Me-
chanics,” In: K. Ford, Ed., Statistical Physics, Benjamin,
New York, 1963, pp. 181-218.
[73] G. Chaitin, “On the Length of Programs for Computing
Finite Binary Sequences,” Journal of the Association for
Computing Machinery, Vol. 13, 1966, pp. 547-569.
[74] G. Chaitin, “Randomness and Mathematical Proof,” Sci-
entific American, Vol. 232, No. 5, 1975, pp. 47-52.
doi:10.1038/scientificamerican0575-47
[75] L. Brillouin, “Science and Information Theory,” 2nd
Edition, Academic Press, New York, 1962.
[76] J. Kestin and J. R. Dorfman, “Course in Statistical Ther-
modynamics,” Academic Press, New York, 1971.
[77] F. Reif, “Fundamentals of Statistical and Thermal Phys-
ics,” McGraw-Hill, Singapore, 1965.
[78] D. R. Brooks, P. H. Leblond and D. D. Cumming, “In-
formation and Entropy in a Simple Evolution Model,”
Journal of Theoretical Biology, Vol. 109, No. 1, 1984, pp.
77-93. doi:10.1016/S0022-5193(84)80112-5
[79] D. R. Brooks and E. O. Wiley, “Evolution as an Entropic
Phenomenon,” In: J. W. Pollard, Ed., Evolutionary The-
ory: Paths to the Future, John Wiley and Sons, London,
1984, pp. 141-171.
[80] J. Campbell, “Grammatical Man: Information, Entropy,
Language, and Life,” Simon & Schuster, New York, 1982.
[81] N. Wiener, “Cybernetics: Or Control and Communication
in the Animal and the Machine,” MIT Press, Massachu-
setts, 1948.
[82] J. S. Wicken, “Entropy, Information, and Nonequilibrium
Evolution,” Systematic Zoology, Vol. 32, No. 4, 1983, pp.
438-443. doi:10.2307/2413170
[83] L. Kari and L. F. Landweber, “Biocomputing in Ciliates,”
In: M. Amos, Ed., Cellular Computing, Oxford Univer-
sity Press, Oxford, 2003.
[84] R. D. Knight, L. F. Landweber and M. Yarus, “How Mi-
tochondria Redefine the Code,” Journal of Molecular
Evolution, Vol. 53, No. 4-5, 2001, pp. 299-313.
doi:10.1007/s002390010220
[85] G. Burger, I. Plante, K. M. Lonergan and M. W. Gray,
“The Mitochondrial DNA of the Amoeboid Protozoon,
Acanthamoeba Castellanii: Complete Sequence, Gene

L. F. DEL. CASTILLO ET AL. 391
Content and Genome Organization,” Journal of Molecu-
lar Biology, Vol. 245, No. 5, 1995, pp. 522-537.
doi:10.1006/jmbi.1994.0043
[86] C. H. Waddington, “New Patterns in Genetics and Devel-
opment,” Columbia University Press, New York, 1966.
[87] C. J. Smith, “Problems with Entropy in Biology,” Bio-
systems, Vol. 7, No. 2, 1975, pp. 259-265.
doi:10.1016/0303-2647(75)90033-7
[88] N. H. Gregersen, “From Complexity to Life: on the
Emergence of Life and Meaning,” Oxford University
Press, New York, 2003.
[89] L. Brillouin, “Thermodynamics and Information Theory,”
American Scientist, Vol. 38, 1950, pp. 595-599.
[90] P. A. Corning and S. J. Kline, “Thermodynamics, Infor-
mation and Life. Revisited, Part I: ‘To Be or Entropy’,”
Systems Research and Behavioral Science, Vol. 15, 1998,
pp. 273-295. doi:10.1002/(SICI)1099-1743(199807/08)15:
4<273::AID-SRES200>3.0.CO;2-B
[91] G. J. Vermeij, “Evolution and Escalation,” Princeton
University Press, New Jersey, 1987.
[92] G. J. Vermeij, “The Evolutionary Interaction among Spe-
cies: Selection, Escalation, and Coevolution,” Annual Re-
view of Ecology and Systematics, Vol. 25, 1994, pp.
219-236. doi:10.1146/annurev.es.25.110194.001251
[93] G. J. Vermeij, “Economics, Volcanoes, and Phanerozoic
Revolutions,” Paleobiology, Vol. 21, No. 2, 1995, pp.
125-152.
[94] M. Tribus and E. C. McIrvine, “Energy and Information,”
Scientific American, Vol. 224, 1971, pp. 179-188.
doi:10.1038/scientificamerican0971-179
[95] S. N. Salthe, “The Natural Philosophy of Work,” Entropy,
Vol. 9, No. 2, 2007, pp. 83-99. doi:10.3390/e9020083
[96] E. Mayr, “Toward a New Philosophy of Biology,” Har-
vard University Press, Massachusetts, 1988.
[97] A. Pross, “The Driving Force for Life’s Emergence: Ki-
netic and Thermodynamic Considerations,” Journal of
Theoretical Biology, Vol. 220, No. 3, 2003, pp. 393-406.
doi:10.1006/jtbi.2003.3178
[98] S. Chandrasekhar, “Hydrodynamic and Hydromagnetic
Stability,” Clarendon, Oxford, 1961.
[99] D. D. Joseph, “Stability of Fluid Motions,” Springer,
Berlin, 1976.
[100] A. Movchan, “The Direct Method of Lyapounov in Sta-
bility Problems of Elastic Systems,” Journal of Applied
Mathematics and Mechanics, Vol. 23, No. 3, 1959, pp.
483-693. doi:10.1016/0021-8928(59)90161-3
[101] A. J. Pritchard, “A Study of the Classical Problem of
Hydrodynamic Stability,” IMA Journal of Applied Ma-
thematics, Vol. 4, No. 1, 1968, pp. 78-93.
doi:10.1093/imamat/4.1.78
[102] G. Nicoli and I. Prigogine, “Self-Organization in Non-
Equilibrium Systems: From Dissipative Structures to Or-
der through Fluctuations,” Wiley-Interscience, New York,
1977.
[103] P. Glandsdorv and I. Prigogine, “Structure, Stabilité et
Fluctuations,” Masson, Paris, 1971.
[104] D. Kondepudi, R. J. Kaufman and N. Singh, “Chiral
Symmetry-Breaking in Sodium-Chlorate Crystallization,”
Science, Vol. 250, No. 4983, 1990, pp. 975-976.
doi:10.1126/science.250.4983.975
[105] V. Castets, E. Dalos, J. Boissonade and P. de Kepper,
“Experimental Evidence of Sustained Standing Turing-
Type Nonequilibrium Chemical Patterns,” Physical Re-
view Letters, Vol. 64, No. 24, 1990, pp. 2953-2956.
doi:10.1103/PhysRevLett.64.2953
[106] Q. Ouyang and H. L. Swinney, “Transition from a Uni-
form State to Hexagonal and Striped Turing Patterns,”
Nature, Vol. 352, No. 6336, 1991, pp. 610-612.
doi:10.1038/352610a0
[107] A. M. Turing, “The Chemical Basis of Morphogenesis,”
Philosophical Transactions of the Royal Society of Lon-
don. Series B - Biological Sciences, Vol. 237, No. 641,
1952, pp. 37-72. doi:10.1098/rstb.1952.0012
[108] M. Tabor, “Chaos and Integrability in nonlinear Dynam-
ics: An Introduction,” Wiley-Interscience, USA, 1989.
[109] P. Davies, “The New Physics: A Synthesis,” In: P. Davies,
Ed., The New Physics, Cambrige Unversity Press, Cam-
bridge, 1989.
[110] J. Swift and P. C. Hohenberg, “Hydrodynamic Fluctua-
tions at the Convective Instability,” Physical Review A,
Vol. 15, No. 1, 1977, pp. 319-328.
doi:10.1103/PhysRevA.15.319
[111] M. C. Cross and P. C. Hohenberg, “Pattern Formation
Outside of Equilibrium,” Reviews of Modern Physics, Vol.
65, No. 3, 1993, pp. 851-1112.
doi:10.1103/RevModPhys.65.851
[112] K. Ito and Y. P. Gunji, “Self-Organization of Living Sys-
tems towards Criticality at the Edge of Chaos,” Biosys-
tems, Vol. 33, No. 1, 1994, pp. 17-24.
doi:10.1016/0303-2647(94)90057-4
[113] E. Bodenschatz, W. Pesch and G. Ahlers, “Recent De-
velopments in Rayleigh-Bénard Convection,” Annual Re-
view of Fluid Mechanics, Vol. 32, No. 1, 2000, pp.
709-778. doi:10.1146/annurev.fluid.32.1.709
[114] P. L. Engle, “Conjectures Concerning Complexity and
Hierarchy,” Far from Equilibrium, Laurel Highlands Me-
dia, Greensburg, 2002.
[115] J. Walleczek, “Self-Organized Biological Dynamics and
Nonlinear Control: Toward Understanding Complexity,
Chaos and Emergent Function in Living Systems,” Cam-
bridge University Press, Cambridge, 2000.
[116] R. Luzzi, A. R. Vasconcelos and J. G. Ramos, “Predictive
Statistical Mechanics: A Nonequilibrium Ensamble For-
mulation,” Kluwer Academia Publishers, Dordrecht, 2002.
[117] R. A. Eve, S. Horsfall and M. E. Lee, “Chaos, Complex-
ity, and Sociology: Myths, Models, and Theories,” Sage
Publications, London, 1997.
[118] R. Boyd and P. J. Richerson, “Culture and the Evolution-
ary Process,” University of Chicago Press, London, 1988.
[119] L. L. Cavalli-Sforza and M. W. Feldman, “Cultural Trans-
mission and Evolution: A Quantitative Approach,” Prince-
ton University Press, New Jersey, 1981.